はじめに
原則として、いくつかの種類の証券が金融市場で取引されています:国債、地方債、企業株など。
市場参加者が無料のお金を持っている場合、それは銀行に持ち込まれ、利子を受け取るか、その上で証券を購入し、追加の収入を受け取ることができます。 しかし、どの銀行に含めるのでしょうか? どの証券を購入しますか?
低リスクの証券は一般的に低利回りですが、高利回りの証券は通常よりリスクが高くなります。 経済科学はこの問題を解決するためのいくつかの推奨事項を提供できますが、このためには、適切なソフトウェアが必要です。
証券ポートフォリオを分析するためのソフトウェアツールは、利回り行列を処理し、厳密および非厳密な不等式の形で制限された非線形計画問題を解決する必要があります。 いくつかのタイプの非線形計画問題のPythonでの象徴的な解決策。私はすでに出版物で検討しました[1]。 ただし、深刻な不平等という形での制限により、この出版物で提案されている方法を証券ポートフォリオの分析に適用することは不可能です。
この出版物の目的は、scipy.optimizeライブラリを使用して証券ポートフォリオを最適化する方法を開発することです。 ターゲットの機能に対する追加の制限の導入として、このライブラリのこのようなあまり知られていない機能をプログラミングするとき、私は調査して適用しなければなりませんでした[2]。
最適なポートフォリオ問題Markowitzの声明
市場参加者が証券の取得に費やすことを望む資本の分配に関する一般的な問題を考えてみましょう。 投資家の目標は、資本を保護する方法でお金を投資し、可能であればそれを増やすことです。
市場参加者が保有する証券のセットは、ポートフォリオと呼ばれます。 ポートフォリオの価値は、その構成銘柄すべての合計価値です。 今日、その値がPであり、1年でP 'に等しくなる場合、(P'-P)/ Pポートフォリオの利回りを年率(%)で呼び出すのが自然です。 ポートフォリオリターンは、価値の単位あたりのリターンです。
xiを i番目のタイプの証券の購入に費やした資本の割合とします。 割り当てられたすべての資本は単位として扱われます。 diを 1通貨単位あたりのi番目のタイプの年間証券のパーセントでの利回りとします。
収益性は時間とともに変動するため、ランダム変数と見なします。 mi 、 riを平均期待収益率およびリスクと呼ばれる標準偏差とします。 CVijにより、i番目とj番目のタイプの証券の利回りの共分散を示します。
有価証券のポートフォリオの各所有者は、ジレンマに直面しています。効率を高め、リスクを減らしたいと考えています。 ただし、「1石で2羽の鳥を捕まえることはできない」ため、効率とリスクのどちらかを選択する必要があります。
リスクを最小限に抑え、一定の利益をもたらすマルコウィッツの最適なポートフォリオモデル
方程式系および不等式の形式のそのようなモデルは、形式[3]を持ちます。

x1、x2 ... xnを決定する必要があります。
計算の初期データは、次の形式の証券の利回りマトリックスです(プログラムリストのマトリックスの完成例)。

Pythonで最小リスクモデルを実装するには、次の開発手順を完了する必要があります。
1.株式1-6の平均利益率の決定:
from sympy import * import numpy as np from scipy.optimize import minimize from sympy import * import numpy as np from scipy.optimize import minimize "D- ( )" D=np.array([[9.889, 11.603,11.612, 12.721,11.453,12.102], [12.517, 13.25,12.947,12.596,12.853,13.036], [12.786, 12.822,15.447,14.452,15.143,16.247], [11.863, 12.114,13.359,13.437,11.913,15.300], [11.444, 13.292,13.703,11.504,13.406,15.255], [14.696, 15.946,16.829,17.698,16.051,17.140]],np.float64) d= np.zeros([6,1])# m,n= D.shape# for j in np.arange(0,n): for i in np.arange(0,m): d[j,0]=d[j,0]+D[i,j] d=d/n print(" 1-6 : \n %s"%d)
取得するもの:
平均在庫は1-6を返します:
[[12.19916667]
[13.17116667]
[13.98283333]
[13.73466667]
[13.46983333]
[14.84666667]]
2.共分散行列の構築(m = n = 6)。
CV = np.zeros([m、n])
np.arange(0、m)のiの場合:
np.arange(0、n)のjの場合:
x = np.array(D [0:m、j])。T
y = np.array(D [0:m、i])。T
X = np.vstack((x、y))
CV [i、j] = round(np.cov(x、y、ddof = 0)[1,0]、3)
print( "共分散行列CV:\ n%s"%CV)
取得するもの:
CV共分散行列:
[[2.117 1.773 2.256 2.347 2.077 1.975]
[1.773 1.903 1.941 2.049 1.888 1.601]
[2.256 1.941 2.901 2.787 2.701 2.761]
[2.347 2.049 2.787 3.935 2.464 2.315]
[2.077 1.888 2.701 2.464 2.723 2.364]
[1.975 1.601 2.761 2.315 2.364 3.067]]
3.ポートフォリオ収益の分散を決定する関数のシンボリック定義(リスク関数)。
x1,x2,x3,x4,x5,x6,x7,x8,p,q,w=symbols(' x1 x2 x3 x4 x5 x6 x7 x8 pqw' , float= True) v1=Matrix([x1,x2,x3,x4,x5,x6]) v2=v1.T w=0 for i in np.arange(0,m): for j in np.arange(0,n): w=w+v1[p.subs({p:i}),q.subs({q:0})]*v2[p.subs({p:0}),q.subs({q:j})]*CV[p.subs({p:i}),q.subs({q:j})] print(" ( ):\n%s"%w)
取得するもの:
ポートフォリオリターンの分散(リスク関数):
2.117 * x1 ** 2 + 3.546 * x1 * x2 + 4.512 * x1 * x3 + 4.694 * x1 * x4 + 4.154 * x1 * x5 + 3.95 * x1 * x6 + 1.903 * x2 ** 2 + 3.882 * x2 * x3 + 4.098 * x2 * x4 + 3.776 * x2 * x5 + 3.202 * x2 * x6 + 2.901 * x3 ** 2 + 5.574 * x3 * x4 + 5.402 * x3 * x5 + 5.522 * x3 * x6 + 3.935 * x4 ** 2 + 4.928 * x4 * x5 + 4.63 * x4 * x6 + 2.723 * x5 ** 2 + 4.728 * x5 * x6 + 3.067 * x6 ** 2
4.最小のリスクと収益性のための最適な株式ポートフォリオの決定mp = 13.25
def objective(x):# x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6\ + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2 \ + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6 \ + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2 def constraint1(x):# -1 return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0 def constraint2(x): # return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - 13.25 x0=[1,1,0,0,0,1]# b=(0.0,1.0)# x bnds=(b,b,b,b,b,b)# () con1={'type':'ineq','fun':constraint1} # () con2={'type':'eq','fun':constraint2} # () cons=[con1,con2]# () sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons)# print(" -%s"%str(round(sol.fun,3))) print(" 1 - %s, - %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print(" 2 - %s, - %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print(" 3 - %s, - %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print(" 4 - %s, - %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print(" 5 - %s, - %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print(" 6 - %s, - %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
取得するもの:
最小リスク関数-1.846
シェア1シェア-0.141、収益性-1.721
シェア2シェア-0.73、リターン-9.616
シェア3シェア-0.0、収益性-0.0
シェア4シェア-0.0、収益性-0.0
株式5株-0.0、収益性-0.0
株式6株-0.129、リターン-1.914
結論:
収益性は1,2,6株です。 これは、出版物の冒頭で提起された質問に対する回答の一部です。
所定の収益性に対するマルコウィッツ法によるリスクを最小限に抑えるプログラムの完全なリスト
from sympy import * import numpy as np from scipy.optimize import minimize "D- ( )" D=np.array([[9.889, 11.603,11.612, 12.721,11.453,12.102], [12.517, 13.25,12.947,12.596,12.853,13.036], [12.786, 12.822,15.447,14.452,15.143,16.247], [11.863, 12.114,13.359,13.437,11.913,15.300], [11.444, 13.292,13.703,11.504,13.406,15.255], [14.696, 15.946,16.829,17.698,16.051,17.140]],np.float64) d= np.zeros([6,1])# m,n= D.shape# for j in np.arange(0,n): for i in np.arange(0,m): d[j,0]=d[j,0]+D[i,j] d=d/n print(" : \n %s"%d) CV= np.zeros([m,n]) for i in np.arange(0,m): for j in np.arange(0,n): x=np.array(D[0:m,j]).T y=np.array(D[0:m,i]).T X = np.vstack((x,y)) CV[i,j]=round(np.cov(x,y,ddof=0)[1,0],3) print(" CV: \n %s"%CV) x1,x2,x3,x4,x5,x6,x7,x8,p,q,w=symbols(' x1 x2 x3 x4 x5 x6 x7 x8 pqw' , float= True) v1=Matrix([x1,x2,x3,x4,x5,x6]) v2=v1.T w=0 for i in np.arange(0,m): for j in np.arange(0,n): w=w+v1[p.subs({p:i}),q.subs({q:0})]*v2[p.subs({p:0}),q.subs({q:j})]*CV[p.subs({p:i}),q.subs({q:j})] print(" ( ):\n%s"%w) def objective(x):# x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6\ + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2 \ + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6 \ + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2 def constraint1(x):# -1 return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0 def constraint2(x): # return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - 13.25 x0=[1,1,0,0,0,1]# b=(0.0,1.0)# x bnds=(b,b,b,b,b,b)# () con1={'type':'ineq','fun': constraint1} # () con2={'type':'eq','fun': constraint2} # () cons=[con1,con2]# () sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons)# print(" -%s"%str(round(sol.fun,3))) print(" 1 - %s, - %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print(" 2 - %s, - %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print(" 3 - %s, - %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print(" 4 - %s, - %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print(" 5 - %s, - %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print(" 6 - %s, - %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
最大の収益性と所定の(許容可能な)リスクの最適なMarkowitzポートフォリオ
連立方程式と不等式の形式は次のとおりです。
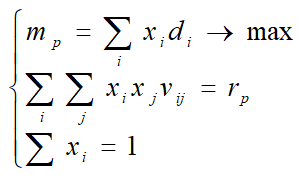
Pythonで与えられたリスクで最大の収益性のポートフォリオの最適化
import numpy as np from scipy.optimize import minimize d=np.array( [[ 12.19916667], [ 13.17116667], [ 13.98283333], [ 13.73466667], [ 13.46983333], [ 14.84666667]]) def constraint2(x): x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 \ + 3.95*x1*x6 + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 \ + 2.901*x3**2 + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 \ + 4.63*x4*x6 + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2-2 def constraint1(x): return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0 def objective(x): return -(12.199*x[0] + 13.171*x[1] + 13.983*x[2] + 13.735*x[3] + 13.47*x[4]+ 14.847*x[5] ) x0=[1,1,1,1,1,1] b=(0.0,1.0) bnds=(b,b,b,b,b,b) con1={'type':'ineq','fun':constraint1} con2={'type':'eq','fun':constraint2} cons=[con1,con2] sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons) print(" -%s"%str(round(sol.fun,3))) print(" 1 - %s, - %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print(" 2 - %s, - %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print(" 3 - %s, - %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print(" 4 - %s, - %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print(" 5 - %s, - %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print(" 6 - %s, - %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
前の例ですべてが詳述されているように、リストの一部は自明です。 ただし、違いがあります。 平均収益性dの列と条件関数def constraint2(x)は前の例から取られ、前の例では最小リスク関数でした。 さらに、新しい目的関数の値-def Objective(x)を出力する前に最大値を決定するために、マイナス記号が設定されます。
結果:
最大利回り関数--14.1
シェア1シェア-0.0、収益性-0.0
シェア2シェア-0.72、リターン-9.489
シェア3シェア-0.0、収益性-0.0
シェア4シェア-0.0、収益性-0.0
株式5株-0.0、収益性-0.0
シェア6シェア-0.311、リターン-4.611
利益2.6を共有します。 ただし、scipy最適化最小化を使用した最適化結果はこれだけではありません。 Mathcadを使用して、同じ問題の解決策と結果を比較することにしました。これが私が得たものです。

Mathcadは、同じ数の2.6の有益な株式を指しますが、株式は異なります。 Pythonでは、Mathcad 0.539で0.720、0.311、0.461、それぞれ最大戻り値は14.1および13.9です。 どのプログラムが最適を正しく計算するかを最終的に確認するために、MathcadでPythonで取得したシェアの値を代入します。

結論:Pythonでは、Mathcadを使用する場合よりも、関数の最適値、つまりシェアと収益性がより正確に計算されます。
トービンのモデルに従った最適な証券ポートフォリオの形成
最小リスクトービンポートフォリオ:
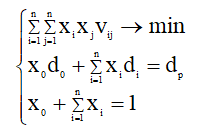
ここで、d0-危険な有価証券のない効率;
x0-リスクフリー証券に投資された資本のシェア。
xi、xj-i番目とj番目のタイプの証券に投資された資本の割合。
di-i番目の証券の利回りの数学的期待値(算術平均)。
vijは、i番目とj番目のタイプの証券の有効性の間の相関モーメントです。
たとえば、次の数値x0 = 0.3、d0 = 10、dp = 12.7を使用して、特定の収益の資本のシェアを選択し、総収益を設定します。
Pythonでのトービンの最小リスクポートフォリオの実装
import numpy as np from scipy.optimize import minimize d=np.array( [[ 12.19916667], [ 13.17116667], [ 13.98283333], [ 13.73466667], [ 13.46983333], [ 14.84666667]]) x00=0.3;d0=10;dp=12.7 def objective(x):# x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6\ + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2 \ + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6 \ + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2 def constraint1(x):# -1 return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0+x00 def constraint2(x): # return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - dp+x00*d0 x0=[1,1,1,1,1,1]# b=(-1.0,100.0)# x bnds=(b,b,b,b,b,b)# () con1={'type':'ineq','fun':constraint1} # () con2={'type':'eq','fun':constraint2} # () cons=[con1,con2]# () sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons)# print(" : %s"%str(round(sol.fun,3))) print(" 1 - %s, : %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print(" 2 - %s, : %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print(" 3 - %s, : %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print(" 4 - %s, : %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print(" 5 - %s, : %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print(" 6 - %s, : %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
取得するもの:
最小リスク関数:0.728
株式1株--0.023、リターン:-0.286
シェア2シェア-0.666、リターン:8.778
株式3株-1.0、リターン:-13.983
株式4株-0.079、リターン:1.089
株式5株-0.3、リターン:4.048
株式6株-0.677、リターン:10.054
有益なのは株式2,4,5,6です。
最大効率のトービンのポートフォリオ

ここで、rpはポートフォリオリスクです。
PythonでTobinの最大効率のポートフォリオを実装する
import numpy as np from scipy.optimize import minimize x00=0.8;d0=10;rp=0.07 d=np.array( [[ 12.19916667], [ 13.17116667], [ 13.98283333], [ 13.73466667], [ 13.46983333], [ 14.84666667]]) def constraint2(x): x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 \ + 3.95*x1*x6 + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 \ + 2.901*x3**2 + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 \ + 4.63*x4*x6 + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2-rp def constraint1(x): return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0+x0 def objective(x): return -(d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5]+x00*d0) x0=[1,1,1,1,1,1] b=(-1.0,100.0) bnds=(b,b,b,b,b,b) con1={'type':'ineq','fun':constraint1} con2={'type':'eq','fun':constraint2} cons=[con1,con2] sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons) print(" : %s"%str(round(sol.fun,3))) print(" 1 - %s, : %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print(" 2 - %s, : %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print(" 3 - %s, : %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print(" 4 - %s, : %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print(" 5 - %s, : %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print(" 6 - %s, - %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))
取得するもの:
最大降伏関数:-11.657
株式1株-0.09、リターン:1.096
ストック2シェア-0.196、リターン:2.583
株式3株-1.0、リターン:-13.983
株式4株-0.113、収益性:1.552
株式5株-0.411、リターン:5.538
株式6株-0.463、リターン-6.872
収益性のある株式は1,2,4,5です。
結論:
Pythonを初めて使用して、MarkowitzモデルとTobinモデルを使用して証券ポートフォリオを最適化する問題を解決しました。
Mathcad数学パッケージとの比較例は、scipy最適化最小化ライブラリの利点を示しています。
参照: