運動方程式の統合

物理学のシミュレーションは、物理学の法則に基づいて小さな予測を行います。 これらの予測は実際には非常に単純で、「オブジェクトがここにあり、この方向にその速度で移動した場合、短期間でここに来る」などです。 統合と呼ばれる数学的手法を使用して、このような予測を作成します。



この記事のトピックは、まさにそのような統合の実装です。

運動方程式の統合

高校または高校のコースから、力は質量と加速の積に等しいことを思い出すことができます。

$$

$$F = ma$$

この方程式を変換すると、加速度は力を質量で割ったものに等しいことがわかります。 重いオブジェクトは投げにくいため、これは直感的な期待に沿っています。

$$

$$a = f / ma = f / m$$

加速度は、時間の経過に伴う速度の変化率です。

$$

$$dv / dt = a = F / m$$

同様に、速度は位置が時間とともに変化する速度です。

$$

$$dx / dt = v$$

つまり、オブジェクトの現在の位置と速度、およびオブジェクトに加えられた力がわかれば、特定の時点での位置と速度を見つけるために統合できます。

数値積分

大学で微分方程式を研究していない場合は、簡単に呼吸できます。微分方程式を解析的に解くことはないので、それらを研究した人々とほぼ同じ状況にあります。 代わりに、 数値積分による解決策を模索します。



これが数値積分の仕組みです。まず、開始位置と速度から開始し、次に少し先に進んで将来の速度と位置を見つけます。 次に、これを繰り返し、小さなステップで前進し、前の計算の結果を次の計算の開始点として使用します。



しかし、どの段階で速度と位置の変化を見つけるのでしょうか？



答えは運動方程式にあります 。



現在の時間t 、および時間ステップdtまたは「デルタ時間」と呼びましょう。



これで、運動方程式をわかりやすい方法で表現できます。

 加速度=力/質量
    位置の変化=速度* dt
    速度変化=加速度* dt 

直観的には、これは理解できることです。60km / hの速度で移動している車の場合、1時間で60 kmを運転します。 同様に、毎秒10 km / hで加速する車は、10秒で100 km / h速く移動します。



もちろん、このロジックは、加速度と速度が一定の場合にのみ保持されます。 しかし、たとえそれらが変わっても、最初はこれはかなり良い近似です。



これをコードで想像してみましょう。 1キログラムの静止物体から始め、10 kN（キロニュートン）の一定の力をそれに加え、1つの時間ステップが1秒に等しいと仮定して、一歩前進します。

double t = 0.0; float dt = 1.0f; float velocity = 0.0f; float position = 0.0f; float force = 10.0f; float mass = 1.0f; while ( t <= 10.0 ) { position = position + velocity * dt; velocity = velocity + ( force / mass ) * dt; t += dt; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果は次のとおりです。

  t=0: position = 0 velocity = 0 t=1: position = 0 velocity = 10 t=2: position = 10 velocity = 20 t=3: position = 30 velocity = 30 t=4: position = 60 velocity = 40 t=5: position = 100 velocity = 50 t=6: position = 150 velocity = 60 t=7: position = 210 velocity = 70 t=8: position = 280 velocity = 80 t=9: position = 360 velocity = 90 t=10: position = 450 velocity = 100
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、すべてのステップでオブジェクトの位置と速度の両方がわかります。 これは数値積分です。

明示的オイラー法

使用したばかりの統合は、 明示的オイラー法と呼ばれます。



この技法を最初に発見したスイスの数学者レナード・オイラーにちなんで名付けられました。



オイラー積分は、数値積分の最も単純な手法です。 タイムステップの変化率が一定の場合にのみ、100％の精度が得られます。



上記の例では加速度は一定であるため、速度積分にはエラーがありません。 ただし、速度を統合して位置を取得し、加速により速度が増加します。 これは、統合された位置でエラーが発生することを意味します。



しかし、この間違いはどれほど大きいのでしょうか？ 見つけよう！



一定の加速度でオブジェクトの動きを分析するソリューションがあります。 これを使用して、数値的に統合された位置と正確な結果を比較できます。

  s = ut + 0.5at ^ 2
     s = 0.0 * t + 0.5at ^ 2
     s = 0.5（10）（10 ^ 2）
     s = 0.5（10）（100）
     s = 500メートル 

10秒後、オブジェクトは500メートル移動するはずですが、オイラー法では明示的に450の結果が得られます。つまり、わずか10秒で最大50メートルのエラーが発生します。



これは信じられないほど悪いようですが、ゲームでは通常、物理学のステップにそれほど大きな時間間隔は取られません。 実際、物理学は通常、表示フレームレートにほぼ等しい周波数で計算されます。



ステップdt = 1⁄100を設定すると、より良い結果が得られます。

  t=9.90: position = 489.552155 velocity = 98.999062 t=9.91: position = 490.542145 velocity = 99.099060 t=9.92: position = 491.533142 velocity = 99.199059 t=9.93: position = 492.525146 velocity = 99.299057 t=9.94: position = 493.518127 velocity = 99.399055 t=9.95: position = 494.512115 velocity = 99.499054 t=9.96: position = 495.507111 velocity = 99.599052 t=9.97: position = 496.503113 velocity = 99.699051 t=9.98: position = 497.500092 velocity = 99.799049 t=9.99: position = 498.498077 velocity = 99.899048 t=10.00: position = 499.497070 velocity = 99.999046
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、これは非常に良い結果であり、ゲームには間違いなく十分です。

オイラーの明示的方法が（常に）それほど良くない理由

十分に小さな時間ステップでは、一定の加速度を伴う明示的なオイラー法はかなりまともな結果をもたらしますが、加速度が一定でない場合はどうなりますか？



可変加速の良い例は、スプリングショックアブソーバーシステムです。



このシステムでは、質量がバネに取り付けられ、その動きは摩擦などによって抑制されます。 オブジェクトまでの距離に比例する力がオブジェクトを開始点に引き寄せ、オブジェクトの速度に比例する力が反対方向に向けられ、速度が低下します。



ここでは、タイムステップ中の加速度は正確に変化しますが、この絶えず変化する機能は、位置と速度の組み合わせであり、タイムステップ中に絶えず変化します。



減衰のある調和発振器の例です。 これはよく研究された問題であり、数値積分の結果を検証するために使用できる分析ソリューションがあります。



弱減衰システムから始めましょう。このシステムでは、質量が開始点の近くで振動し、徐々に減速します。



質量ばねシステムへの入力は次のとおりです。

• 重量：1キログラム
• 開始位置：開始点から1000メートル
• フックの弾性係数：k = 15
• フックの法則減衰係数：b = 0.1

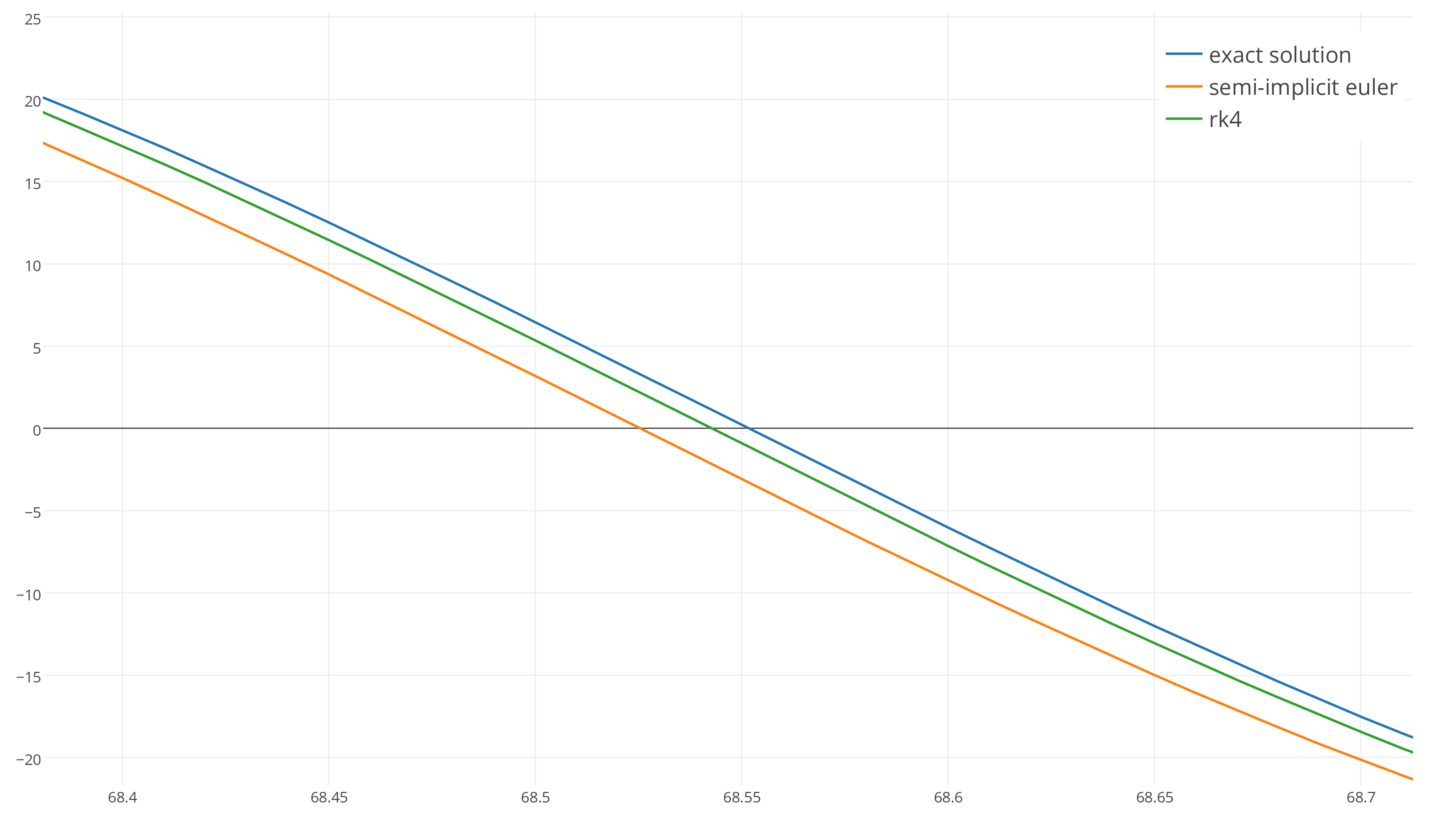
そして、これが正確な解のグラフです：











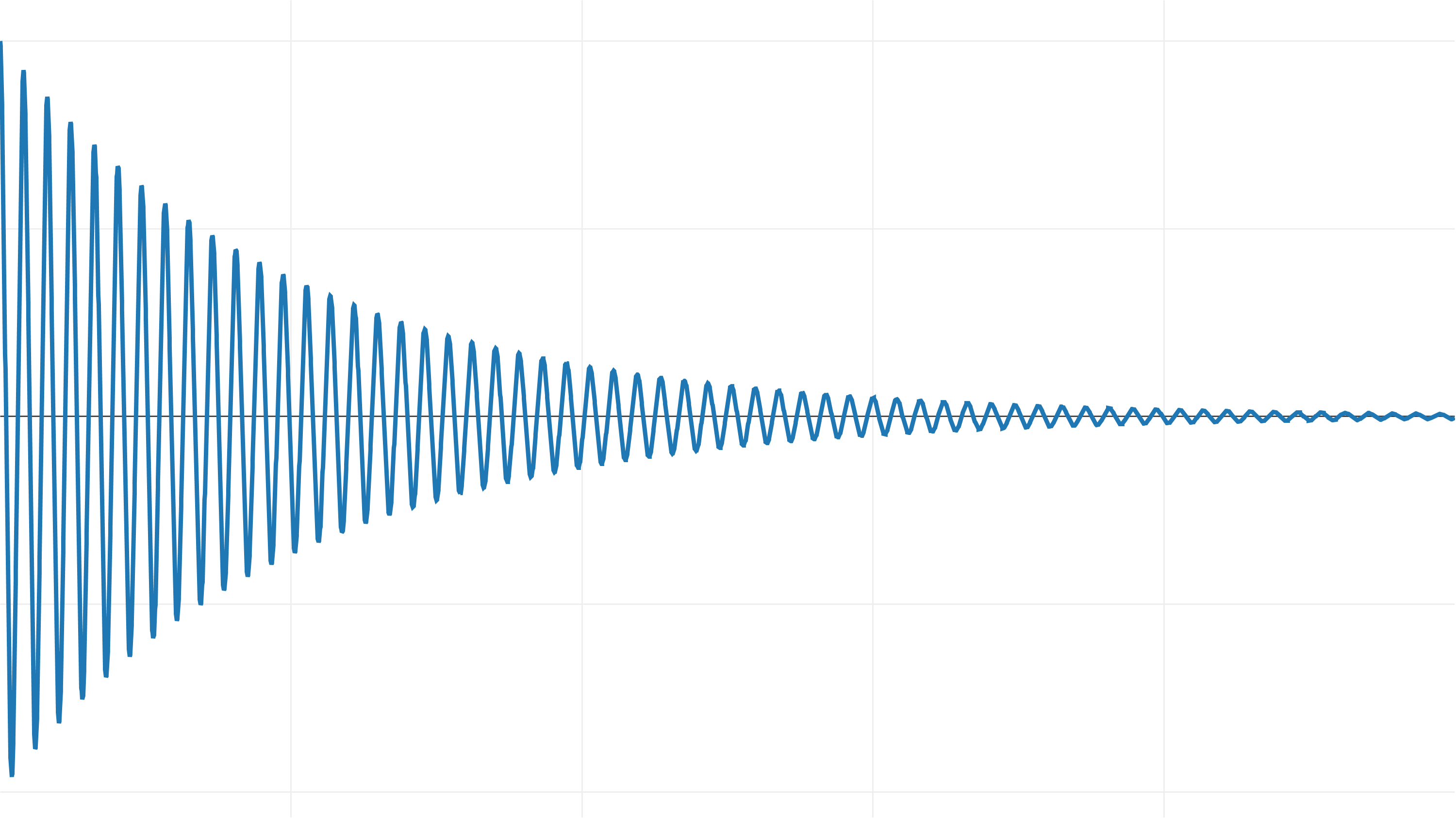
明示的なオイラー法を使用してこのシステムを統合すると、次の結果が得られます。これを垂直にスケーリングしました。











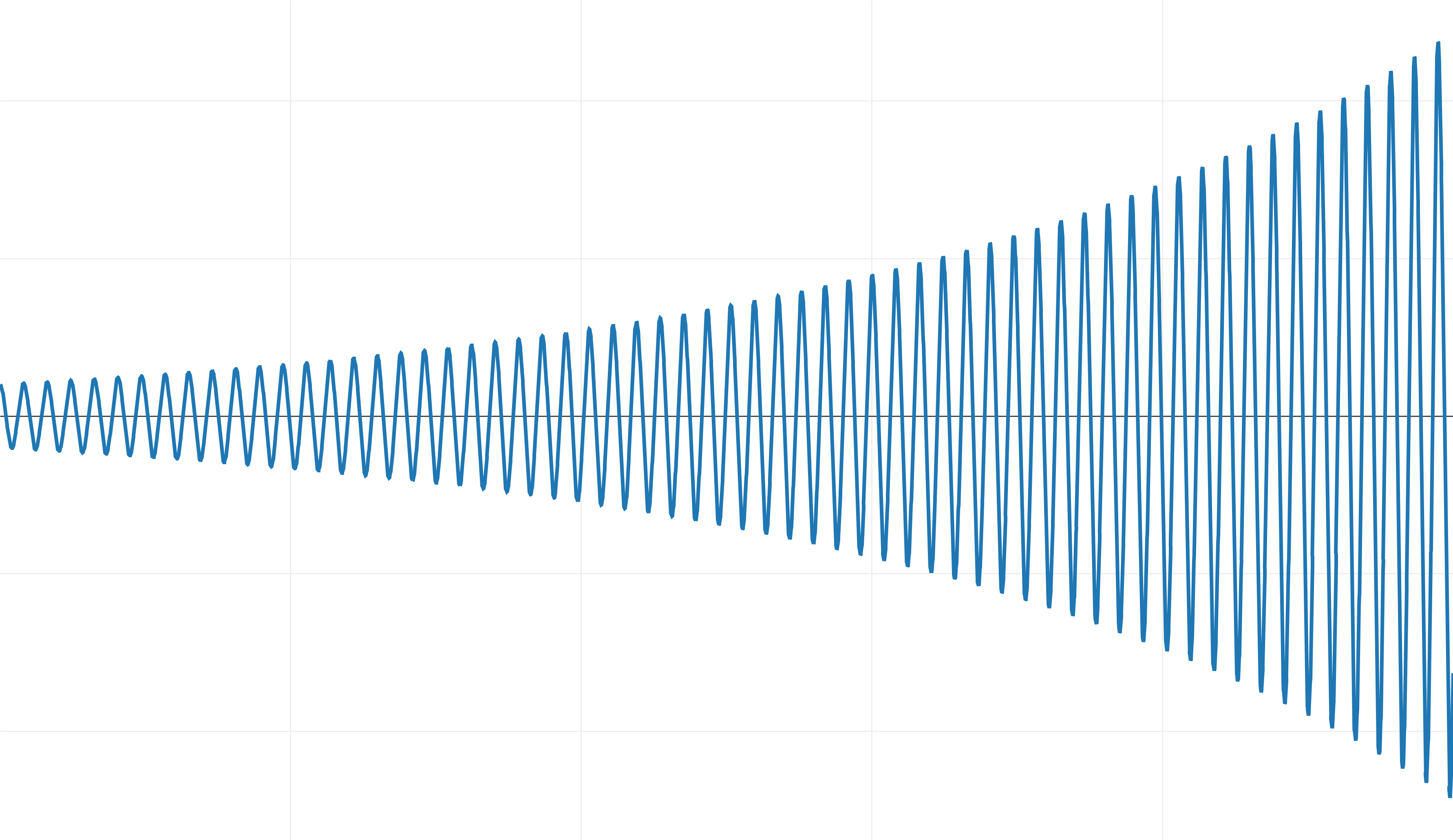
減衰して開始点に近づく代わりに、システムは時間とともにエネルギーを獲得します！



オイラーによって明示的に統合され、 dt = 1⁄100の場合_、このようなシステムは不安定です。



残念ながら、すでに小さなタイムステップで統合されているため、精度を向上させる実用的な方法はありません。 タイムステップを短縮しても、この動作を得るための弾性係数kは常に存在します。

シンプレクティックオイラー法

別の積分器- シンプレクティックオイラー法を考えることができます。



ほとんどの商用ゲーム物理エンジンはこのインテグレーターを使用します。



明示的なオイラー法からシンプレクティックオイラー法への移行は、以下の置換のみで構成されます。

  position += velocity * dt; velocity += acceleration * dt;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

に：

  velocity += acceleration * dt; position += velocity * dt;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

スプリングショックアブソーバーシステムにdt = 1⁄100のシンプレクティックオイラー積分器を使用すると、正確な解に非常に近い安定した結果が得られます。











シンプレクティックオイラー法の精度は明示的方法（1次）と同程度ですが、運動方程式を積分すると、 シンプレクティックであるため、はるかに良い結果が得られます。

他にも多くの統合方法があります。

そして今、何かが完全に異なっています。



陰的オイラー法は、他の方法で不安定になる硬い方程式を統合するのに適した統合法です。 その欠点は、各タイムステップで連立方程式を解く必要があることです。



Verlet統合は、暗黙のオイラー法よりも高い精度を提供し、多数の粒子をシミュレートするときに必要なメモリが少なくなります。 これは2度目の積分器であり、シンプレクティックでもあります。



Runge-Kuttaメソッドと呼ばれるインテグレーターのファミリーがあります 。 実際、明示的なオイラー法はこのファミリーの一部と見なされますが、高次のインテグレーターも含まれます。その中で最も古典的なものは、ルンゲクッタ4次法または単にRK4です。



このインテグレーターのファミリーは、それらを発見したドイツの物理学者にちなんで命名されました： カールルンゲとマーティンクッタ 。



RK4は4次の積分器です。つまり、累積誤差は4次導関数の次数を持ちます。 これにより、メソッドは非常に正確になり、明示的および暗黙的なオイラーメソッド（一次のみ）よりもはるかに正確になります。



しかし、より正確ですが、RK4が自動的に「最良の」積分器になる、またはシンプレクティックオイラー法よりも優れているとは言えません。 すべてがはるかに複雑です。 それでも、それはかなり興味深いインテグレーターであり、調査する価値があります。

RK4の実装

RK4で使用される数学については、すでに多くの説明があります。 例： here 、 hereおよびhere 。 その派生を研究し、それが数学的なレベルでどのように、なぜ機能するかを理解することを強くお勧めします。 しかし、この記事の対象読者は数学者ではなくプログラマーであるため、ここでは実装のみを検討します。 それでは始めましょう。



始める前に、オブジェクトの状態をC ++の構造体として設定して、位置と速度を1か所に便利に保存できるようにします。

  struct State { float x; //  float v; //  };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

導出された状態値を保存するための構造も必要です。

  struct Derivative { float dx; // dx/dt =  float dv; // dv/dt =  };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、1組の導関数を使用してtからt + dtまでの物理状態を計算し、新しい状態で導関数を計算する関数が必要です。

  Derivative evaluate( const State & initial, double t, float dt, const Derivative & d ) { State state; state.x = initial.x + d.dx*dt; state.v = initial.v + d.dv*dt; Derivative output; output.dx = state.v; output.dv = acceleration( state, t+dt ); return output; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

加速機能は、シミュレーション全体を制御します。 スプリングショックアブソーバーシステムで使用して、単位質量の加速度を返しましょう。

  float acceleration( const State & state, double t ) { const float k = 15.0f; const float b = 0.1f; return -k * state.x - b * state.v; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

もちろん、ここで何を書く必要があるかは、シミュレーションに依存しますが、与えられた状態と時間でこのメソッド内の加速度を計算できるようにシミュレーションを構成する必要があります。そうしないと、RK4インテグレーターでは機能しません。



最後に、統合手順自体を取得します。

  void integrate( State & state, double t, float dt ) { Derivative a,b,c,d; a = evaluate( state, t, 0.0f, Derivative() ); b = evaluate( state, t, dt*0.5f, a ); c = evaluate( state, t, dt*0.5f, b ); d = evaluate( state, t, dt, c ); float dxdt = 1.0f / 6.0f * ( a.dx + 2.0f * ( b.dx + c.dx ) + d.dx ); float dvdt = 1.0f / 6.0f * ( a.dv + 2.0f * ( b.dv + c.dv ) + d.dv ); state.x = state.x + dxdt * dt; state.v = state.v + dvdt * dt; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

RK4インテグレーターは、4点で導関数をサンプリングして、曲率を決定します。 導関数aがbの計算に使用され、bがcの計算に使用され、cがdに使用されることに注意してください。 次の計算への現在の導関数のこの転送は、積分器RK4にその精度を与えます。



これらの量の変化率が時間の関数または状態自体の関数である場合、これらの導関数a、b、c、およびdのそれぞれが異なることが重要です。 たとえば、スプリングショックアブソーバーシステムでは、加速度は現在の位置と速度の関数であり、時間ステップで変化します。



4つの導関数を計算した後、 テイラー級数の展開から得られた加重和として、最適な総導関数が計算されます。 この結合された導関数は、明示的なオイラー積分器で行ったように、位置を移動し、時間を早めるために使用されます。

シンプレクティックオイラー法とRK4の比較

インテグレーターRK4をテストしましょう。



明らかに、それは高次の積分器であるため（4番目と1番目）、オイラーのシンプレクティック法よりも明らかに正確になりますよね？











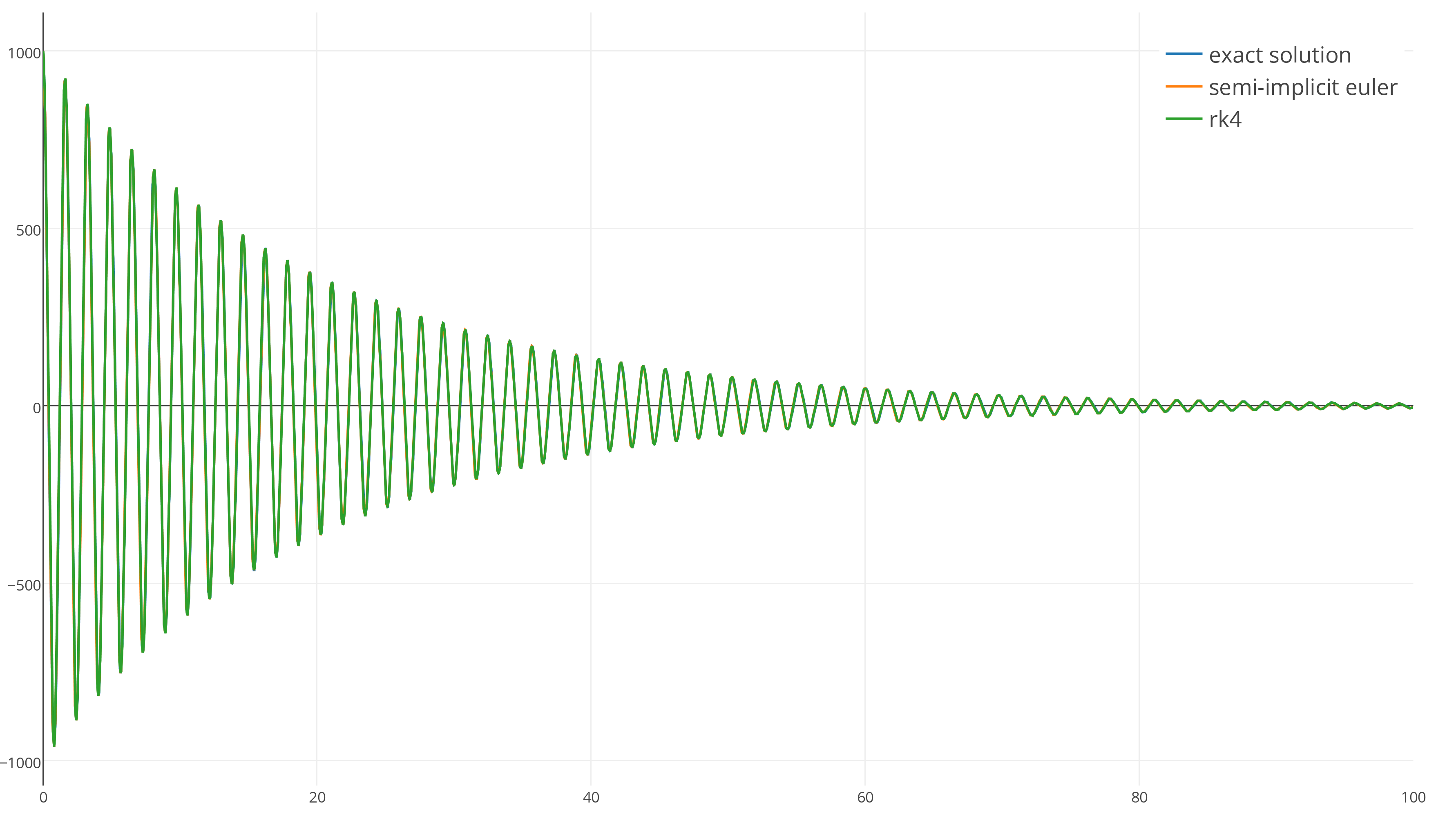
真実ではない 。 両方の積分器は正確な結果に非常に近いため、このスケールでは両者の違いを見つけることはほとんど不可能です。 どちらの積分器も安定しており、 dt = 1⁄100で正確な解を非常によく繰り返します。









RK4がシンプレクティックオイラー法よりも正確であることは明らかですが、この精度はRK4の複雑さと余分な実行時間に見合うだけですか？ 判断が難しい。



2つのインテグレーターの間に大きな違いを見つけることができるかどうか試してみましょう。 残念ながら、このシステムはすぐにゼロにフェードするため、このシステムを長時間観察することはできません。そこで、減衰せずに無限に振動する単純な調和振動子に移りましょう。



これが私たちが努力する正確な結果です：











インテグレーターのタスクを複雑にするために、タイムステップを0.1秒に増やしましょう。



次に、インテグレーターを90秒間実行し、ズームインします。











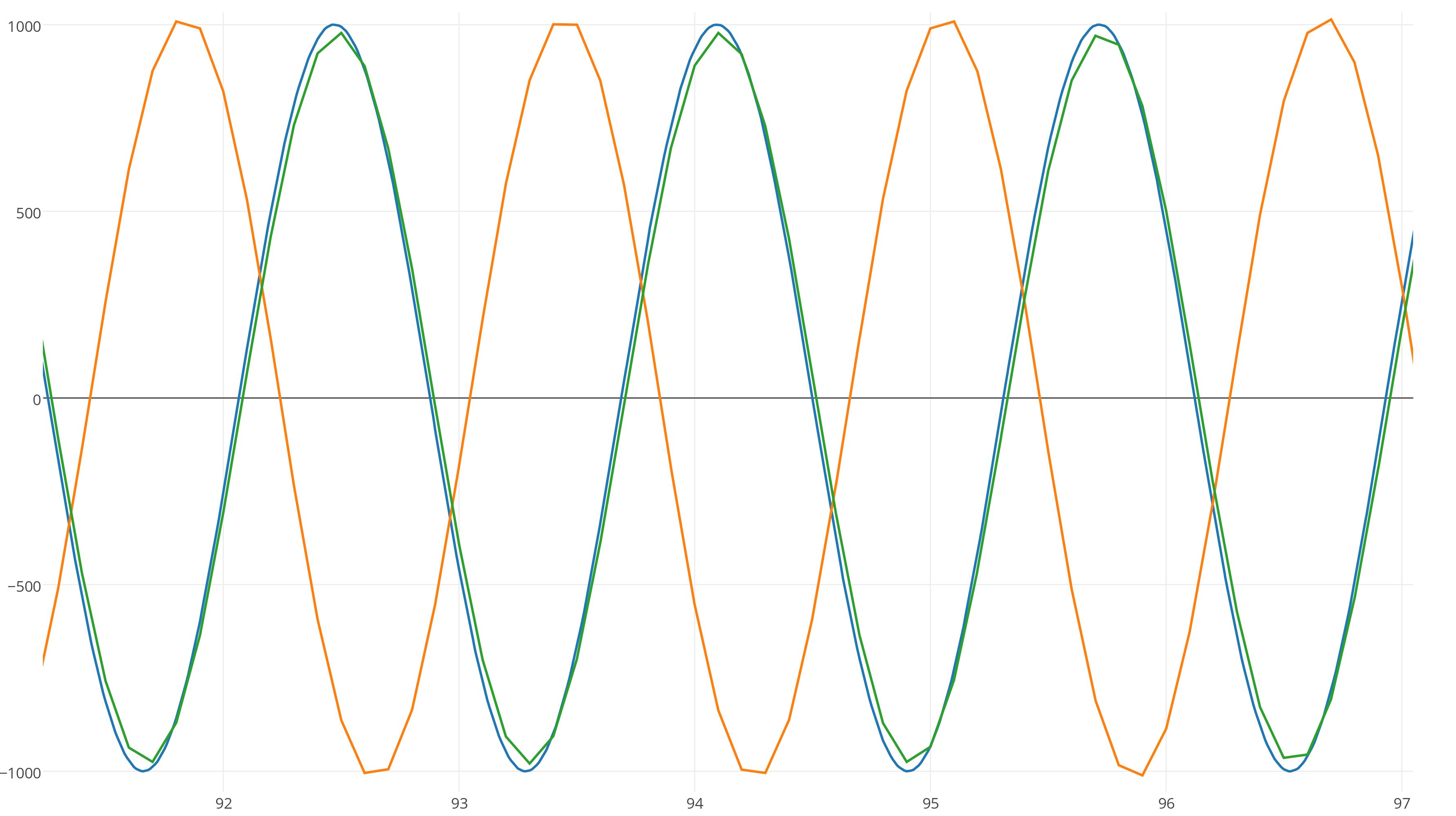
90秒後、オイラーシンプレクティック法（オレンジ色の曲線）は周波数がわずかに異なるため、正確な解に対して位相がシフトしましたが、緑色のRK4曲線は周波数に対応しますが、エネルギーを失います！



タイムステップを0.25秒に増やすと、これにはっきりと気付くことができます。



RK4は正しい周波数を維持しますが、エネルギーを失います：











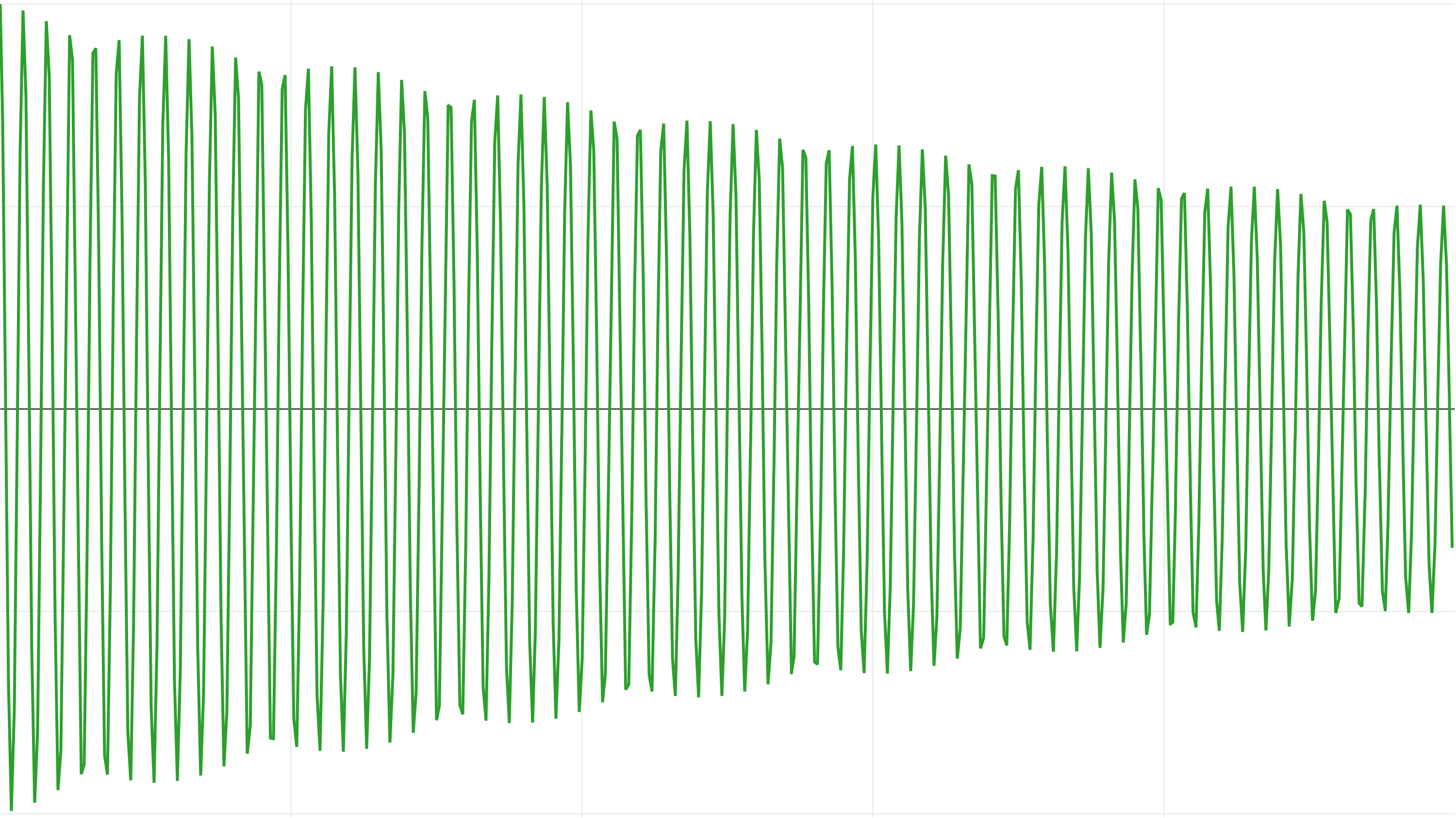
そして、平均でオイラーシンプレクティック法はエネルギーをはるかに節約します：











しかし、フェーズからの移行から。 なんて面白い結果でしょう！ ご覧のとおり、RK4の精度が高い場合、必ずしも「より良い」とは限りません。 この問題には多くのニュアンスがあります。

おわりに

3つの異なるインテグレーターを実装し、結果を比較しました。

1. 明示的オイラー法
2. シンプレクティックオイラー法
3. 順序4のルンゲクッタ法（RK4）

それでは、どのインテグレーターをゲームで使用する必要がありますか？



同情オイラー法をお勧めします。 「安価」で実装が簡単で、明示的なオイラー法よりもはるかに安定しており、平均して、極端な条件に近い場合でもエネルギーを節約する傾向があります。



シンプレクティックオイラー法よりも高い精度が本当に必要な場合は、 ハミルトニアンシステム用に設計された高次シンプレクティックインテグレータを調べることをお勧めします 。 このようにして、RK4よりもシミュレーションに適した、より高度な高次統合手法を学習します。



そして最後に、まだこのようなゲームで書いている場合：

 位置+ =速度* dt;
    速度+ =加速度* dt; 

次に、1秒を費やしてこれらの行を次のように置き換えます。

 速度+ =加速度* dt;
    位置+ =速度* dt; 

私を信じて、あなたはこれについて幸せになるでしょう。