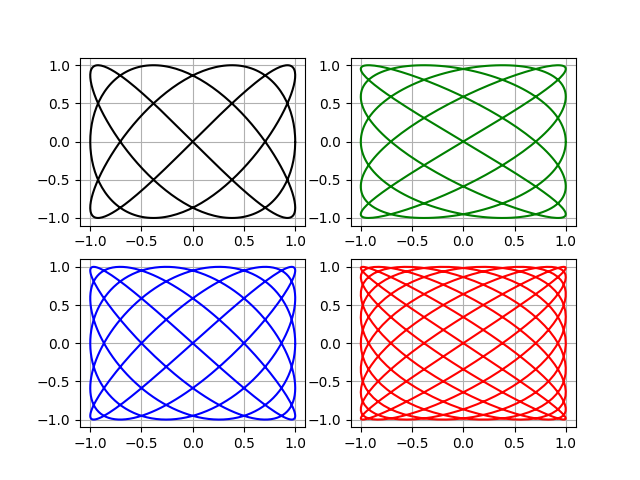
はじめに
出版物[1]は、リサージュ図を使用して周波数の比を測定する方法のPythonでの実装を詳細に検討しました。 例として、振動レベルゲージのカンチレバー楕円管の振動形態を分析しました[2]。
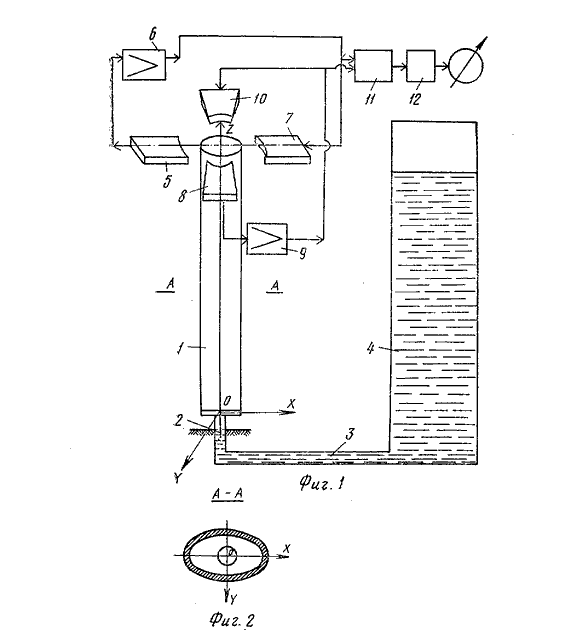
自励システム5,6,7を使用した楕円断面の弾性的に固定されたチューブは、1つの平面で自励振動を行い、システム8、9、10の助けを借りて、最初の平面に垂直な別の平面で自励振動します。 チューブは、互いに近い周波数の異なる2つの相互に垂直な平面で振動します。 チューブの質量は、チューブを満たす液体のレベルに依存します。
質量が変化すると、チューブの振動周波数も変化します。これは、レベルゲージの出力信号です。 周波数は、周波数がマイクロプロセッサ11によって処理されるときに補償される乗法および加法追加誤差に関する追加情報を運びます。
チューブの振動周波数の充填液のレベルへの依存性を決定する問題は未解決のままであり、この刊行物の主題である。
問題の声明
出版物[1]からのチューブの曲げ線の正確な方程式を使用して、レイリー法により2つの相互に垂直な平面におけるチューブの曲げ振動の周波数を決定します。
得られた周波数の関係を使用して、レベルに対する感度の依存関係を見つけ、液体レベルの制御に適した範囲を決定します。
Pythonツールを使用してこれらのタスクを実装するには、記号と文字数値を解決する2つの方法を検討してください。 これらのパフォーマンスメソッドを比較する
楕円片持ち管の振動周波数を決定するためのレイリー法の適用
レイリー法の本質は、保守的な振動系の最大運動Tmaxおよび最大ポテンシャルPmaxエネルギーを決定し、その後、エネルギーTmax = Pmaxを等化することです。
得られた方程式から、すべての高調波成分が最大値に等しくなるという事実を考慮して、システムの振動の周波数を見つけることができます。たとえば、sin(t * w)** 2 = 1およびcos(t * w)** 2 = 1です。
Pythonシンボリックソリューション
チューブの曲げ線に次の方程式を適用します。
z =(sin(k * x)-sinh(k * x)+((cosh(k)-cos(k))/(sin(k)-sinh(k)))*(cos(k * x) -cosh(k * x)))。
k = 1.875での最初の波形で、関数-def fp(L)によって長さLの空のチューブの運動エネルギーを計算するプログラムの次のリストを記述します。
def fp(L): x,A, L, w, t, k =symbols('x AL wtk ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(t))**2 return factor(integrate(dx2,(x,0,L)))/(A**2*w**2*cos(t*w)**2)
チューブをレベルhまで満たし、チューブ全体で振動する液体の運動エネルギーについては、断面積が小さいため、関数def fh(h)を取得します。
def fh(h): x,A, h, w, t, k =symbols(' x A hwtk ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(t))**2 return factor(integrate (dx2,(x,0,h)))/(A**2*w**2*cos(t*w)**2)
チューブのポテンシャルエネルギーの場合、関数def pl(L)は次の形式になります。
def pl(L): x,A, J, w, t, k,L =symbols('x AJ wtk L ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(x))**2 return factor(integrate (dx2,(x,0,L)))/(A**2*sin(t*w)**2)
これで、レイリー方程式–Tmax = Pmaxを作成できます。これを行うには、関数def fp(L)、def fh(h)、def pl(L)に係数(A ** 2 * w ** 2 * cos(t * w )** 2)および(A ** 2 * sin(t * w)** 2)、リストに分割されています。 なぜ最初に除算し、次に乗算するのか、後でシンボル数値法を検討するときに説明します。
運動エネルギー関数に、チューブと液体の単位長さの質量-m0およびmを掛けます。 ポテンシャルエネルギー関数に剛性E * Jを掛けます。 循環周波数-wのレイリー方程式を解き、循環周波数–f = w / 2 * piに変換すると、次のようになります。
f =(0.5 / pi)*((pl(L))*(E * J)/(m0 * fp(L)+ m * fh(h)))** 0.5
発振周波数の関数を使用すると、記号解を得ることができます。
キャラクターソリューションリスト
from sympy import * from numpy import arange,pi import matplotlib.pyplot as plt import time start = time.time() def fp(L): x,A, L, w, t, k =symbols('x AL wtk ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(t))**2 return factor(integrate(dx2,(x,0,L)))/(A**2*w**2*cos(t*w)**2) def fh(h): x,A, h, w, t, k =symbols(' x A hwtk ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(t))**2 return factor(integrate (dx2,(x,0,h)))/(A**2*w**2*cos(t*w)**2) def pl(L): x,A, J, w, t, k,L =symbols('x AJ wtk L ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(x))**2 return factor(integrate (dx2,(x,0,L)))/(A**2*sin(t*w)**2) """ """ L,h,m,m0,E,J,q =symbols(' L,h m0 m EJ q ') k1=q.subs({q:0.16}) k2=pl(L).subs({L:1}) k3=E.subs({E:196e9})*J.subs({J:2.3e-08}) k4=m0.subs({m0:1.005}) k5=m.subs({m:0.98}) k6=fp(L).subs({L:1}) """ """ x=arange(0.0,1.0,0.01) f=k1*((k2+k3)/(k4*k6+k5*fh(h)))**0.5 y=[k1*((k2+k3)/(k4*k6+k5*fh(h).subs({h:w})))**0.5 for w in arange(0.0,1.0,0.01)] s=f.diff(h) y1=[s.subs({h:w}) for w in arange(0.0,1.0,0.01)] k3=E.subs({E:196e9})*J.subs({J:1.7e-08}) f1=k1*((k2+k3)/(k4*k6+k5*fh(h)))**0.5 y2=[k1*((k2+k3)/(k4*k6+k5*fh(h).subs({h:w})))**0.5 for w in arange(0.0,1.0,0.01)] s1=f1.diff(h) y3=[s1.subs({h:w}) for w in arange(0.0,1.0,0.01)] k7=fh(h).subs({h:0.7}) k3=E.subs({E:196e9})*J.subs({J:2.3e-08}) f1=k1*((k2+k3)/(k4*k6+k5*k7))**0.5 k3=E.subs({E:196e9})*J.subs({J:1.7e-08}) f2=k1*((k2+k3)/(k4*k6+k5*k7))**0.5 x1=[sin(f1*t) for t in arange(0.,2*pi,0.01)] y4=[sin(f2*t) for t in arange(0.,2*pi,0.01)] """ """ plt.subplot(221) plt.plot(x, y, label='f1-zox') plt.plot(x, y2,label='f2- zoy') plt.xlabel(' h') plt.ylabel(' f 1,f2') plt.legend(loc='best') plt.grid(True) plt.subplot(222) plt.plot(x, y1,label='s=df/dh zox') plt.plot(x, y3,label='s1=df1/dh - zoy') plt.ylabel('s') plt.xlabel(' h ') plt.legend(loc='best') plt.grid(True) plt.subplot(223) plt.plot(x1, y4,label='X,Y h=0.7') plt.ylabel(' Y') plt.xlabel('X') plt.grid(True) plt.legend(loc='best') stop = time.time() print (" :",round(stop-start,3)) plt.show()
結果:
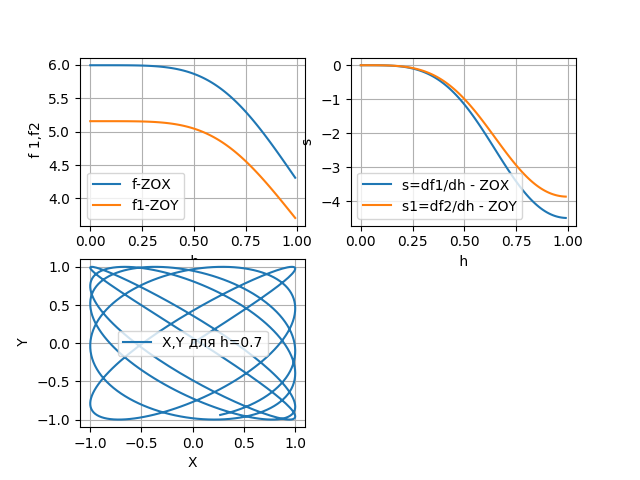
時間:165.868
得られたグラフから、水溶液用のチューブの長さ0.75のLのレベルから測定または制御を実行できることがわかります。 チューブの端で最高の感度。
e-6のオーダーの機械的共振器の周波数の高い安定性を考えると、測定は0.5 Lからより広いセクションで実行できます。また、0.75 Lからのセクションでは、エラーの加法成分と乗法成分の両方を補正してマイクロプロセッサ処理を適用できます。
おわりに
シンボリックソリューションは良い結果をもたらしますが、多くのコンピューター時間がかかります。
Pythonの文字と数値のソリューション
関数def fp(L)、def fh(h)、def pl(L)の記号解を得ることができるので、それらを(A ** 2 * w ** 2 * cos(t * w)** 2に分割しました。 )および(A ** 2 * sin(t * w)** 2)変数の数を2つに減らす-L、h。 また、レベルゲージの感度のシンボリックソリューションを取得します。
これは、次のリストを使用して実行できます。
文字マッピングのヘルパーリスト
from sympy import * from numpy import arange,pi import matplotlib.pyplot as plt import time start = time.time() def fp(L): x,A, L, w, t, k =symbols('x AL wtk ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(t))**2 return factor(integrate(dx2,(x,0,L)))/(A**2*w**2*cos(t*w)**2) def fh(h): x,A, h, w, t, k =symbols(' x A hwtk ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(t))**2 return factor(integrate (dx2,(x,0,h)))/(A**2*w**2*cos(t*w)**2) def pl(L): x,A, J, w, t, k,L =symbols('x AJ wtk L ') z=(sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x))).subs({k:1.875}) dx=z*A*sin(w*t) dx2=(dx.diff(x))**2 return factor(integrate (dx2,(x,0,L)))/(A**2*sin(t*w)**2) L,h,m,m0,E,J,q =symbols(' L,h m0 m EJ q ') f=q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 s=f.diff(h) print(fp(L)) print(fh(h)) print(pl(L)) print(s) stop = time.time() print (" :",round(stop-start,3))
時間:6.696
リストには複数の関数計算が必要ないため、実行時間は6.696秒です。 さらに、一度だけ使用する必要があります。
これで、結果print(fp(L))、print(fh(h))、print(pl(L))、print(s)を次のリストの対応する関数にコピーすることができます。この場合、計算のためにすべての初期データを簡単に変更できます。 テキストが乱雑にならないように、前のリストのように印刷結果を出しません。
文字数値メソッドのリスト
from numpy import (pi,cos,cosh,sin,sinh,arange) import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' import time start = time.time() L=1# . d=1e-3# . e=0.8# .. a0=20e-3# . a=a0+d# . b0=a0*e# . b=b0+d# . E=196e9# /2. rm=7.9e3# /3. rg=1e3# /3. J=(pi/4)*(a**3*b-a0**3*b0)# 4. J1=(pi/4)*(a*b**3-a0*b0**3)# 4. m0=pi*(a*b-a0*b0)*rm# /3 m=pi*(a0*b0)*rg# /3 q=1/(2*pi)# def fp(L):# L return (1.83012983499975*L*sin(1.875*L)**2 + 1.83012983499975*L*cos(1.875*L)**2 - 0.830129834999752*L*sinh(1.875*L)**2 + 0.830129834999752*L*cosh(1.875*L)**2 - 0.869882798951083*sin(1.875*L)**2 + 0.442735911999868*sin(1.875*L)*cos(1.875*L) + 1.73976559790217*sin(1.875*L)*sinh(1.875*L) - 1.9521384906664*sin(1.875*L)*cosh(1.875*L) - 0.885471823999735*cos(1.875*L)*sinh(1.875*L) + 0.976069245333201*sinh(1.875*L)*cosh(1.875*L) - 0.869882798951083*cosh(1.875*L)**2 + 0.869882798951083) def fh(h):# h return (1.83012983499975*h*sin(1.875*h)**2 + 1.14978095631541e-15*h*sin(1.875*h)*sinh(1.875*h) + 1.83012983499975*h*cos(1.875*h)**2 - 1.07791964654569e-15*h*cos(1.875*h)*cosh(1.875*h) - 0.830129834999752*h*sinh(1.875*h)**2 + 0.830129834999752*h*cosh(1.875*h)**2 - 0.869882798951083*sin(1.875*h)**2 + 0.442735911999868*sin(1.875*h)*cos(1.875*h) + 1.73976559790217*sin(1.875*h)*sinh(1.875*h) - 1.9521384906664*sin(1.875*h)*cosh(1.875*h) - 0.885471823999735*cos(1.875*h)*sinh(1.875*h) + 0.976069245333201*sinh(1.875*h)*cosh(1.875*h) - 0.869882798951083*cosh(1.875*h)**2 + 0.869882798951083) def pl(L):# E*J/L**3 return (6.434050201171*L*sin(1.875*L)**2 + 1.48843545191282e-15*L*sin(1.875*L)*sinh(1.875*L) + 6.434050201171*L*cos(1.875*L)**2 - 2.79081647233653e-15*L*cos(1.875*L)*cosh(1.875*L) + 2.918425201171*L*sinh(1.875*L)**2 - 2.918425201171*L*cosh(1.875*L)**2 + 3.0581817150624*sin(1.875*L)**2 - 1.55649344062453*sin(1.875*L)*cos(1.875*L) + 3.11298688124907*sin(1.875*L)*cosh(1.875*L) - 6.86298688124907*cos(1.875*L)*sinh(1.875*L) + 6.1163634301248*cos(1.875*L)*cosh(1.875*L) - 3.0581817150624*sinh(1.875*L)**2 + 3.43149344062453*sinh(1.875*L)*cosh(1.875*L) - 6.1163634301248) def f(m0,q,E,J,h,m):# s=df/dh return -0.5*m0*q*((E*J + 6.434050201171*L*sin(1.875*L)**2 + 6.434050201171*L*cos(1.875*L)**2 + 2.918425201171*L*sinh(1.875*L)**2 - 2.918425201171*L*cosh(1.875*L)**2 + 3.0581817150624*sin(1.875*L)**2 - 1.55649344062453*sin(1.875*L)*cos(1.875*L) + 3.11298688124907*sin(1.875*L)*cosh(1.875*L) - 6.86298688124907*cos(1.875*L)*sinh(1.875*L) + 6.1163634301248*cos(1.875*L)*cosh(1.875*L) - 3.0581817150624*sinh(1.875*L)**2 + 3.43149344062453*sinh(1.875*L)*cosh(1.875*L) - 6.1163634301248)/(m*(1.83012983499975*L*sin(1.875*L)**2 + 1.83012983499975*L*cos(1.875*L)**2 - 0.830129834999752*L*sinh(1.875*L)**2 + 0.830129834999752*L*cosh(1.875*L)**2 - 0.869882798951083*sin(1.875*L)**2 + 0.442735911999868*sin(1.875*L)*cos(1.875*L) + 1.73976559790217*sin(1.875*L)*sinh(1.875*L) - 1.9521384906664*sin(1.875*L)*cosh(1.875*L) - 0.885471823999735*cos(1.875*L)*sinh(1.875*L) - 0.869882798951083*sinh(1.875*L)**2 + 0.976069245333201*sinh(1.875*L)*cosh(1.875*L)) + m0*(1.83012983499975*h*sin(1.875*h)**2 + 1.83012983499975*h*cos(1.875*h)**2 - 0.830129834999752*h*sinh(1.875*h)**2 + 0.830129834999752*h*cosh(1.875*h)**2 - 0.869882798951083*sin(1.875*h)**2 + 0.442735911999868*sin(1.875*h)*cos(1.875*h) + 1.73976559790217*sin(1.875*h)*sinh(1.875*h) - 1.9521384906664*sin(1.875*h)*cosh(1.875*h) - 0.885471823999735*cos(1.875*h)*sinh(1.875*h) - 0.869882798951083*sinh(1.875*h)**2 + 0.976069245333201*sinh(1.875*h)*cosh(1.875*h))))**0.5*(1.0*sin(1.875*h)**2 - 3.26206049606656*sin(1.875*h)*cos(1.875*h) - 2.0*sin(1.875*h)*sinh(1.875*h) + 3.26206049606656*sin(1.875*h)*cosh(1.875*h) + 2.6602596699995*cos(1.875*h)**2 + 3.26206049606656*cos(1.875*h)*sinh(1.875*h) - 5.32051933999901*cos(1.875*h)*cosh(1.875*h) + 1.0*sinh(1.875*h)**2 - 3.26206049606656*sinh(1.875*h)*cosh(1.875*h) + 2.6602596699995*cosh(1.875*h)**2)/(m*(1.83012983499975*L*sin(1.875*L)**2 + 1.83012983499975*L*cos(1.875*L)**2 - 0.830129834999752*L*sinh(1.875*L)**2 + 0.830129834999752*L*cosh(1.875*L)**2 - 0.869882798951083*sin(1.875*L)**2 + 0.442735911999868*sin(1.875*L)*cos(1.875*L) + 1.73976559790217*sin(1.875*L)*sinh(1.875*L) - 1.9521384906664*sin(1.875*L)*cosh(1.875*L) - 0.885471823999735*cos(1.875*L)*sinh(1.875*L) - 0.869882798951083*sinh(1.875*L)**2 + 0.976069245333201*sinh(1.875*L)*cosh(1.875*L)) + m0*(1.83012983499975*h*sin(1.875*h)**2 + 1.83012983499975*h*cos(1.875*h)**2 - 0.830129834999752*h*sinh(1.875*h)**2 + 0.830129834999752*h*cosh(1.875*h)**2 - 0.869882798951083*sin(1.875*h)**2 + 0.442735911999868*sin(1.875*h)*cos(1.875*h) + 1.73976559790217*sin(1.875*h)*sinh(1.875*h) - 1.9521384906664*sin(1.875*h)*cosh(1.875*h) - 0.885471823999735*cos(1.875*h)*sinh(1.875*h) - 0.869882798951083*sinh(1.875*h)**2 + 0.976069245333201*sinh(1.875*h)*cosh(1.875*h))) """ """ x=arange(0.0,1.0,0.01) y1=[q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 for h in arange(0.0,1.0,0.01)] # ZOX J=(pi/4)*(a*b**3-a0*b0**3)# ZOY y2=[q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 for h in arange(0.0,1.0,0.01)]# ZOX J=(pi/4)*(a**3*b-a0**3*b0)# ZOX y3=[f(m0,q,E,J,h,m) for h in arange(0.0,1.0,0.01)]# ZOX J=(pi/4)*(a*b**3-a0*b0**3)# ZOY y4=[f(m0,q,E,J,h,m) for h in arange(0.0,1.0,0.01)]# ZOX J=(pi/4)*(a**3*b-a0**3*b0)# ZOX h=0.7 f1=q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 # h=0.7 ZOX J=(pi/4)*(a*b**3-a0*b0**3)# ZOY f2=q*((pl(L)+E*J)/(m0*fp(L)+m*fh(h)))**0.5 # h=0.7 ZOY x1=[sin(f1*t) for t in arange(0.,2*pi,0.01)]# y5=[sin(f2*t) for t in arange(0.,2*pi,0.01)]# Y """ """ plt.subplot(221) plt.plot(x, y1, label='f-ZOX') plt.plot(x, y2,label='f1-ZOY') plt.xlabel(' h') plt.ylabel(' f 1,f2') plt.legend(loc='best') plt.grid(True) plt.subplot(222) plt.plot(x, y3,label='s1=df1/dh - ZOX') plt.plot(x, y4,label='s2=df2/dh - ZOY') plt.ylabel('s') plt.xlabel(' h ') plt.legend(loc='best') plt.grid(True) plt.subplot(223) plt.plot(x1, y5,label='X,Y h=0.7') plt.ylabel(' Y') plt.xlabel('X') plt.grid(True) plt.legend(loc='best') stop = time.time() print (" :",round(stop-start,3)) plt.show()
結果:
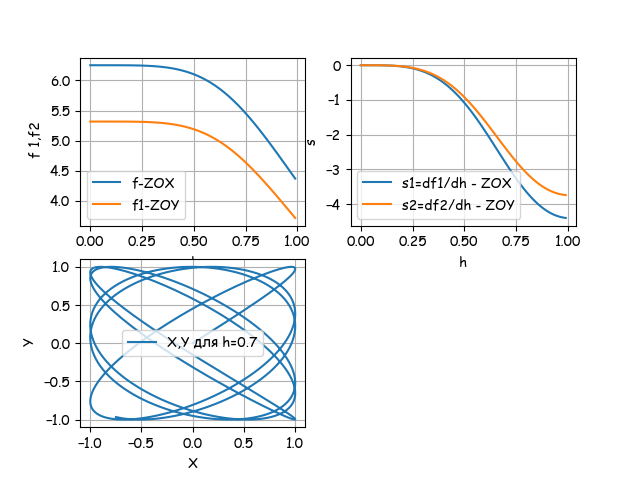
時間:0.447
したがって、シンボリックメソッドと同じ結果が得られましたが、すでに165.868 / 0.447 = 371倍高速です。
チューブが曲げ振動の最初の形で振動する表面
サーフェスを構築するためのリスト
#!/usr/bin/env python #coding=utf8 import pylab import numpy from numpy import (zeros,arange,ones,pi,sin,cos,sinh,cosh) from matplotlib.colors import LinearSegmentedColormap from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D def trubka(): a=10;b=10;k=q[0] v = arange(0, 2.05*pi, 0.05*pi) u= zeros([len(v),1]) for i in arange(0,len(v)): u[i,0]=[sin(k*w)-sinh(k*w)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*w)-cosh(k *w) )for w in arange(0, 2.05*pi, 0.05*pi)][i] x=a*u*cos(v) y=b*u*sin(v) z=u*ones(len(v)) return x,y,z x,y,z=trubka() fig = pylab.figure() axes = Axes3D(fig) axes.plot_surface(x, y, z, rstride=4, cstride=4, cmap = cm.jet) pylab.show()
結果:
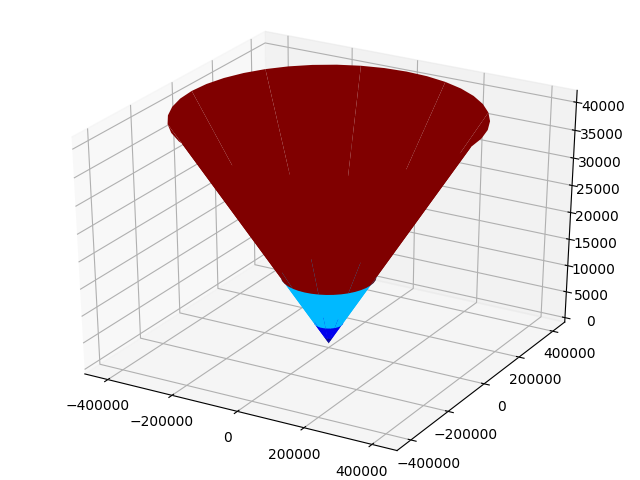
結論:
2つの相互に垂直な平面におけるチューブの曲げ振動の周波数は、チューブの曲げ線の正確な方程式を使用するレイリー法によって決定されました。
得られた周波数の関係を使用して、レベルに対する感度の依存性が検出され、液体レベルの監視または測定に適した範囲が決定されます。
これらのタスクをPythonで実装するには、記号的および記号的数値を解決する2つの方法が考慮されます。 文字数値メソッドは、文字ベースのメソッドよりも370倍高速に実行されます。
参照:
1. リサージュ実験からの2つの音叉から、1世紀のステップを含む1つの楕円レベルゲージチューブまで、すべてPythonで。
2.振動レベル計A.S. No. 777455