
私は常に、複雑なパターンを作成できる基本的なアルゴリズムに魅了されてきました。 このようなアルゴリズムには基本的なものがあります。 そのようなアルゴリズムの1つは、パーフェクトシャッフルです。 その珍しい特性を見てみましょう、またこのアルゴリズムを使用していくつかの印象的なフラクタルを描画してみてください。
その後、たくさんの写真、gifアニメーション、音楽があります。
完全なシャッフルは、マジシャン-ギャンブラーの間で知られています。 彼らは彼をファロシャッフルと呼んでいます。 最近、私はカードのトリックを表示する方法も学びたかった。 トリックはどのように始まりますか? 手の巧みな開発。 1週間カードのデッキを変えた後、彼はシャッフルの基本的な方法をマスターしました-「Riffle Shuffle」、「Faro Shuffle」、「Charlier Pass」。 ファロシャッフルを行うための訓練で、彼はかつてすべての黒いスーツがデッキの先頭にあり、赤いスーツが最後にあるようにデッキを配置しました。 ファロシャッフルを数回行った後、彼はデッキのカードの異常な順序に注意を引きました。 彼はカードを置き、プログラムに座った。
このアルゴリズムは、配列内の要素の順序を変更します(配列をシャッフルします)。 このアルゴリズムは基本です:
1.配列を2つの等しい部分に分割します。
2.配列の前半の要素は偶数位置に配置されます。 第二の-奇数で。
明らかに:
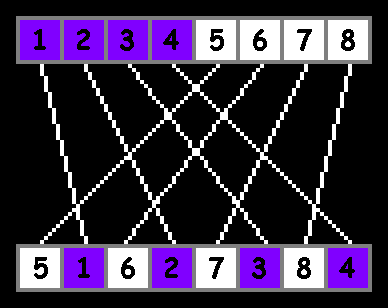
さらに明確に:
JavaScript:
function shuffle(array){ var half=array.length/2; // var temparray=[]; for(var i=0;i<half;i++){ temparray[i*2]=array[i+half]; // temparray[i*2+1]=array[i]; } return temparray; } var array=[1, 2, 3, 4, 5, 6, 7, 8]; array=shuffle(array); console.log(array); // [5, 1, 6, 2, 7, 3, 8, 4]
わずかな余談
このようなパーフェクトシャッフルの変形は、ギャンブラーによってインシャッフルと呼ばれます。 別のオプション(「out-shuffle」)があります-配列の前半の要素は奇数位置に配置されます:
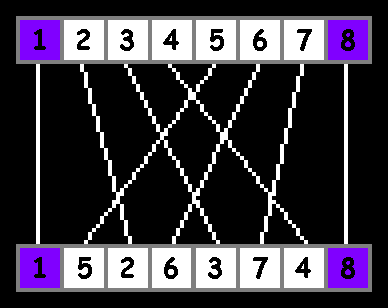
ご覧のように、極端な要素はそれぞれの位置に残り、配列の中央には同じシャッフルが混在しています。 out-shuffleオプションはこれ以上考慮されません。
さらに、配列内の要素の数が奇数の場合、配列の最後の要素がその位置にとどまる場合、オプションを考慮していません。

ご覧のように、極端な要素はそれぞれの位置に残り、配列の中央には同じシャッフルが混在しています。 out-shuffleオプションはこれ以上考慮されません。
さらに、配列内の要素の数が奇数の場合、配列の最後の要素がその位置にとどまる場合、オプションを考慮していません。
アルゴリズムにはいくつかの注目すべき特性があります。 配列を数回混合した場合-n回の反復後、すべての要素は元の位置に戻ります! これは明らかです。 アルゴリズムは決定的です。 配列の後続の状態ごとに、一意の以前の状態が1つだけ存在します。 可能なすべての状態の数は、配列の長さによって制限されます。 配列を繰り返し混合する場合、遅かれ早かれ、可能な状態を使い果たし、第2ラウンドに進みます。 実際、これはもっと早く起こります。 配列を元の状態に戻すのに必要な反復回数は、配列内の要素の数以下です。 反復回数について言えることは、それ以下です。
12要素の配列の場合、12回の反復で十分です。
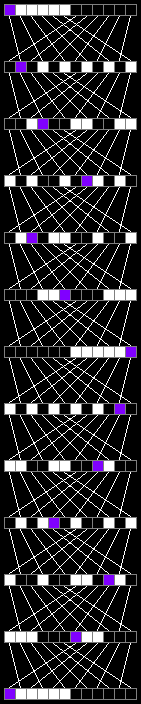
14要素の配列の場合、4回の反復で十分です。
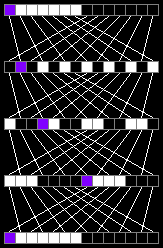
次の図(クリック可能)では、2要素から20までの長さの配列を混合しています:

(シャッフル解除)
リストされたアレイはにリセットされます
2、4、3、6、10、12、4、8、18、6
繰り返し。 シーケンスA002326
Javascript
function a002326(n){ var a=1; var m=0; do{ a*=2; a%=2*n+1; m++; }while(a>1); return m; } for(var n=1;n<11;n++){ m=a002326(n); console.log(m); }
チャートを作成しましょう! X軸に沿ったグラフでは、配列内の要素の数(2で割った値)に注意してください。 y軸は反復回数です。 白い点は、配列の初期状態を示しています(原点は左上隅です)。

同意して、チャート上のポイントはランダムに配置されます。
Perfect Shuffleのもう1つの珍しい特性は、何度も繰り返した後、配列内の要素の順序を逆にすることができることです。 上の図では、12個の要素の配列を混合しました。 要素の順序は、6回目の反復で逆になります。 別のグラフを作成して、要素の逆順で配列をマークします。

繰り返しますが、ドットの配置は混lessとしたものです。
配列内の要素の動きを観察することは非常に興味深いです! 配列全体の前半の要素、特に特定の(最初の)要素。
配列の前半をゼロで埋め、2番目を単位で埋めます(以下、写真のゼロは黒のピクセルで、単位は白です)。 以下の図では、各行( X )は配列の状態です。 Y-反復。
いくつかの配列(142-150要素):





写真はクリック可能です
288要素(144 * 2):

610要素:

他の配列の長さの場合
ちなみに
ご覧のとおり、ここでは継続的なカオスが発生しています。 個別の要素と配列内のその軌道を観察します。
610要素の配列。 最初の要素のみが埋められます:

一般に、単一の要素の場合、配列全体を混在させる必要はありません。 次の反復での特定の要素の位置は、次の式で計算できます。
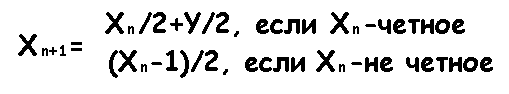
( Yは配列の長さです)
最初の配列(長さ2〜22):

上の図:図の上部、各反復での要素の配列と位置、行の下部-要素のすべての可能な位置。 ご覧のとおり、配列内の要素の軌跡も明らかではありません。 これを確認するために、これらの行から別のグラフを作成し、それらを「スタック」に追加します。
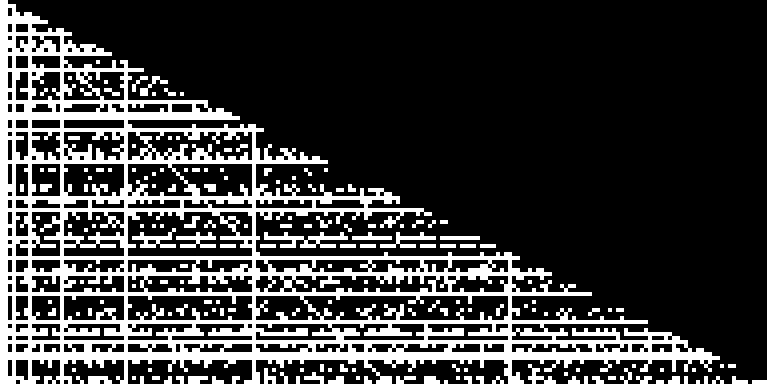
クリック可能
黒いピクセルは、混合時に最初の要素が入らない配列内の位置です。
これで停止できますが、さらに先に進みます! 配列内のすべての要素の動きを観察します。 これを行うために、マトリックスに目を向けます。
しかし、マトリックスの混合に移る前に、配列についてさらに2つのトリックを紹介します。
配列の後半では、要素の順序を逆にします(各反復で):

後半では、要素を反転します。

これらの2つの操作は、依然として有用です。
マトリックスに移りましょう!
マトリックスの最初の行(最初の要素、2番目の行、2番目など)に入力します。 言い換えれば、対角線を描く:

Perfect Shuffleでマトリックスの列をシャッフルします。 したがって、混合後にすべての要素がどこに到達するかがわかります。 マトリックス80x80:
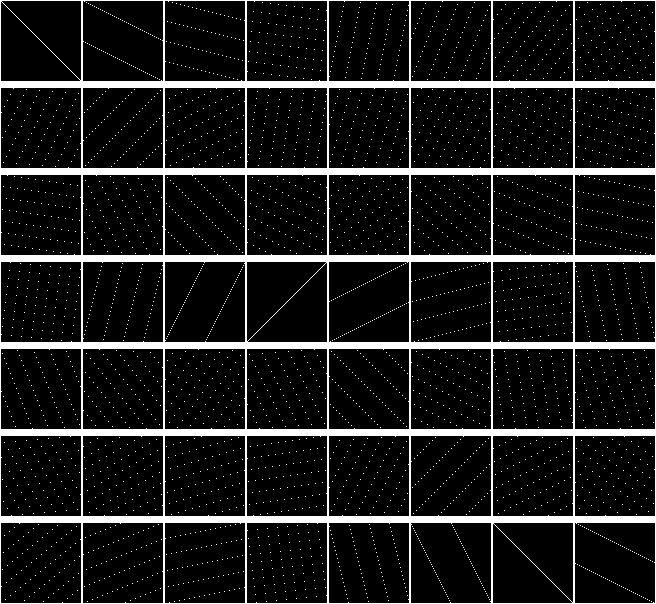
別の対角線が十分でないことは明らかです。

非常に奇妙なモアレが得られます。 27〜35回の反復のマトリックス242x242:

パーフェクトシャッフルを使用してマトリックスの列の混合を既に開始している場合は、行を混合してみませんか?
関数を少し変更します。
行列内の行と列を混合する関数
function shufflecr(array){ var half=array.length/2; var temparray=[]; for(var x=0;x<half;x++){ temparray[x*2]=[]; temparray[x*2+1]=[]; for(var y=0;y<half;y++){ temparray[x*2][y*2]=array[x+half][y+half]; temparray[x*2+1][y*2]=array[x][y+half]; temparray[x*2][y*2+1]=array[x+half][y]; temparray[x*2+1][y*2+1]=array[x][y]; } } return temparray; }
マトリックスを4つの部分に分割します。 列をシャッフルします。 行を混ぜます。 新しい行列を取得します。 明らかに:

対角線はかなり退屈です:

関数のどこかにエラーがあり、マトリックスが混合されていないように見えることさえあります。 対角線を1ピクセル右に移動します。

いいね 関数が機能し、マトリックスがシャッフルされます。 真実は再びかなり退屈です。 マトリックスをある種のパターンで埋めてみましょう。 ランダムな場所に、正方形を描きます:

80x80マトリックスのサイズは偶然選択されませんでした。 長さ80の要素の配列を混合する場合、27回目の反復で、要素の順序が逆になります。
この広場を移動します!
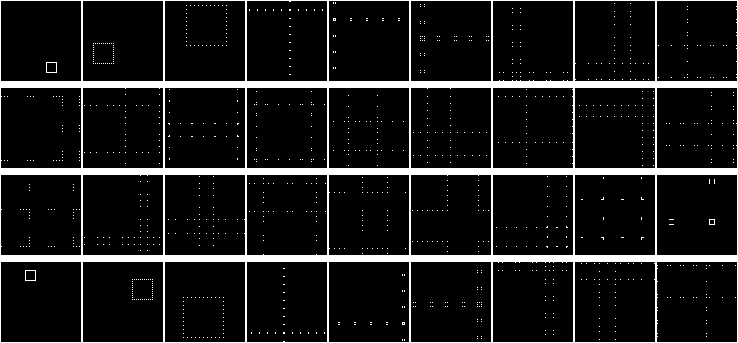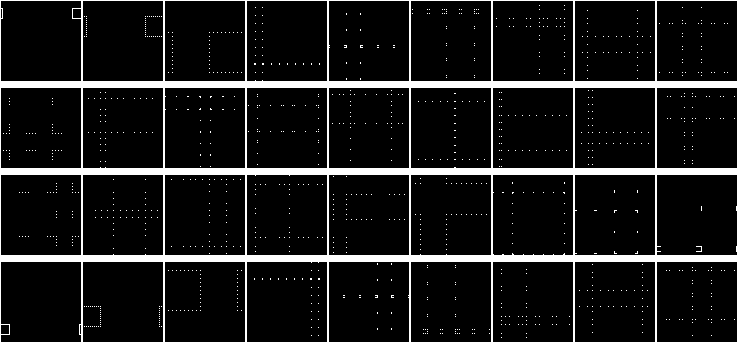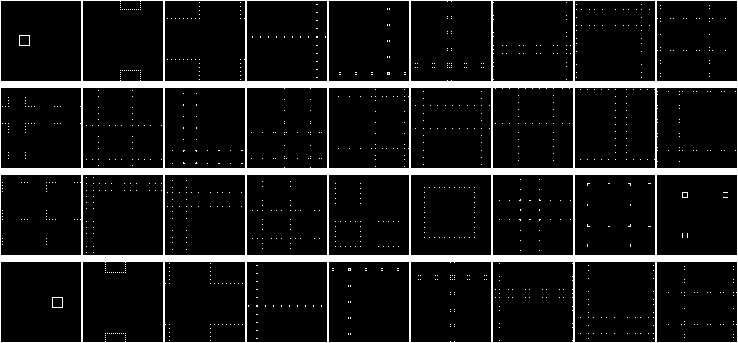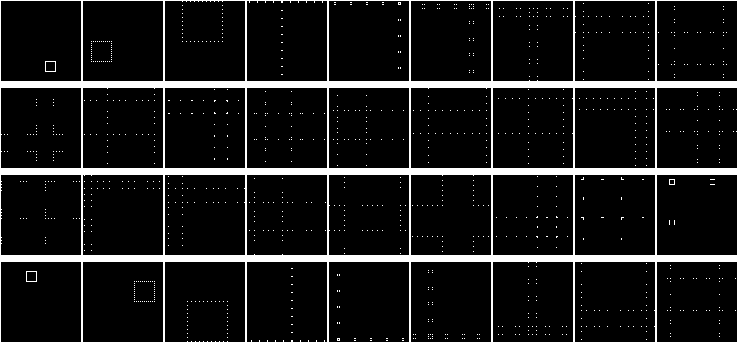
ここでは、非常に興味深いプロパティに注目できますが、円を描くと、このプロパティがさらに良く見えるようになります。

エッジ効果に注意してください。 マトリックスはトーラスに崩壊します! これは、2回目の反復で明らかに見られます。
私たちは移動します:

ちなみに
パーフェクトシャッフルは、三角法と奇妙な関係があります。
上記の配列をシャッフルし、いくつかの素晴らしい写真を得た。 それらの1つ(144 * 2):

また、マトリックスに書き込み、ミックスします。

それともそうです。 元のパターンを取得します。

座標x * 4 + i、y * 4 + jのピクセルを残します。 i = 2、j = 2の場合:

空の列と行を削除します。

他のiおよびj(実際に完全なシャッフル解除-マトリックスを16の部分に分割):

おなじみのパターン! 同様のパターンは、三角関数z = sin(n * x / y)およびz = sin(n * x * y)を使用して描画できます。
関数z = sin(3 * x * y)のグラフ。 z> = 0の場合-白いピクセル。 z <0が黒の場合:

z = sin(13 * x * y):

上記の配列をシャッフルし、いくつかの素晴らしい写真を得た。 それらの1つ(144 * 2):

また、マトリックスに書き込み、ミックスします。

それともそうです。 元のパターンを取得します。

座標x * 4 + i、y * 4 + jのピクセルを残します。 i = 2、j = 2の場合:

空の列と行を削除します。

他のiおよびj(実際に完全なシャッフル解除-マトリックスを16の部分に分割):

おなじみのパターン! 同様のパターンは、三角関数z = sin(n * x / y)およびz = sin(n * x * y)を使用して描画できます。
関数z = sin(3 * x * y)のグラフ。 z> = 0の場合-白いピクセル。 z <0が黒の場合:

z = sin(13 * x * y):

興味深いパターンの1つ:

閉じた領域を選択して入力できます:

ちなみに
古い、親切で愛されているロバ(Internet Explorer)は、Theな画像削減アルゴリズムを使用していません。 彼は、写真からピクセルのn番目の列とn番目の行ごとに単純に取り出して捨てます。 それらを捨てずに別々のマトリックスに入れると、Perfect Shuffle(n = 2)の逆のプロセス(シャッフル解除)が得られます。
これは実際にはかなりクールです! このテンプレートを使用できます。

そして、ロバで少し絞る:
おなじみのパターンを手に入れました。
他のテンプレートで遊ぶことができます:

絞られたロバ:
これは実際にはかなりクールです! このテンプレートを使用できます。

そして、ロバで少し絞る:

おなじみのパターンを手に入れました。
他のテンプレートで遊ぶことができます:

絞られたロバ:

トリックを思い出してください(要素の順序を逆にし、逆にします)。
要素の順序を変更すると、非常に興味深いパターンが得られます! それらの1つ:

塗りつぶしあり:

他のパターンもおもしろいですが、それらについては説明しません。 反転を観察するほうがはるかに興味深いです。
この実験では、空の行列で十分です。 4つの部分に分けます。 それらの2つは可逆です。 シャッフル。 最初の反復では、異常なことは何もありません。

そして、奇妙なパターンが表示されます。

これらのパターンがどこから来たのかを理解するために、再び配列に戻りましょう。 その前に、固定長の行列と配列を使用しました。 アプローチを少し変更してみましょう-長さを徐々に増やします:
1. n要素の配列を作成します。
2.コピーを作成します。
3.完全シャッフルを使用して、コピーをオリジナルとシャッフルします。 n * 2要素の配列を取得しました。
4.ステップ2に戻ります。
コピーを反転するたびに。
2つの要素の配列から始めましょう-1と0
10-ソース配列
10、01-配列および反転コピー
0110-混合
0110、1001-配列と反転コピー
10010110
10010110、01101001
0110100110010110
...など
Morse-Thueシーケンス( A010060 )-最も単純なフラクタルを得ました!
マトリックスに戻ります。 ここから純粋な芸術が始まります。 その前に、マトリックスを4つの部分に分割し、これらの部分を混合しました。 マトリックスをコピーして、コピーに対していくつかの基本的なアクションを実行し、オリジナルとコピーを混ぜてみましょう。
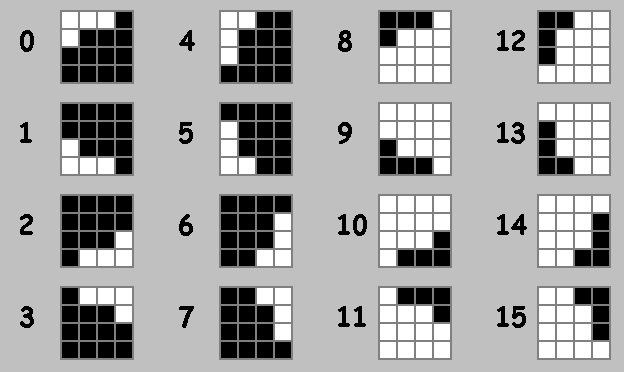
マトリックスを使用すると、15の基本アクションを生成できます。 アクション0-マトリックスは変更されません。 アクション1〜7は、マトリックスを回転させるさまざまな方法です。 アクション8〜15-反転。 明らかに:
例として、コピーに対してアクション0、0、7、7を実行しますステップ7-マトリックスが90°回転します。
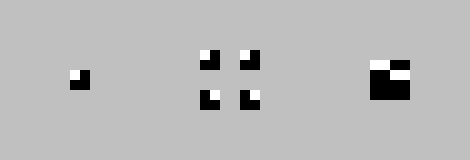
次の反復:
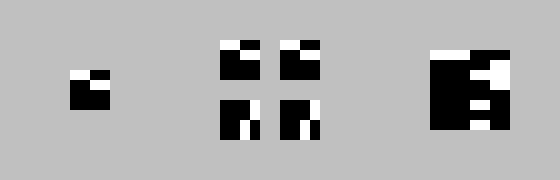
... 8番目の反復:

非常に珍しいフラクタルが判明しました。
ちなみに
私は学生としてフラクタルを描く同様の方法を思いつきました。 マトリックスとパーフェクトシャッフルを混合せずに、同じアクションを実行します。
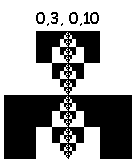
アクション0、0、7、7。最初の反復:

2回目の反復:
8番目:

そして今、2つのトリック。
透明な白いピクセルを上に置いて画像のコピーを置き、コピーを90°回転させます:

垂直方向に回転したコピー:

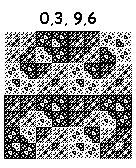
アクション0、0、7、7。最初の反復:

2回目の反復:
8番目:

そして今、2つのトリック。
透明な白いピクセルを上に置いて画像のコピーを置き、コピーを90°回転させます:

垂直方向に回転したコピー:

これらのアクションを組み合わせて、16 ^ 4 = 65536フラクタルを描画できます。 それらのいくつか:
6回の繰り返しで描画されます。 写真はクリック可能です(8回の繰り返し)。








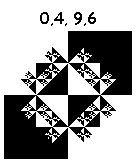














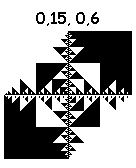






しかし、これらは傑作を引き出します:
15、5、9、5:

3、5、9、5:

13、7、11、11:

0、0、7、13:

1、1、4、14:

他のフラクタルをここに描くことができます。
これらが判明した「カードトリック」です。 これは一時的に停止できると思います(3次元マトリックスを混在させることもできますが、それについては別の機会に)。
この場所を読んだ人のために
私は遺伝的アルゴリズムに基づいてメロディージェネレーターを作成しようとしました。 各曲はノート遺伝子で構成されています。 子孫遺伝子がランダムに混合されている場合、不協和音が得られます。 しかし、パーフェクトシャッフルを使用してそれらをミックスすると、面白いメロディが得られます。 それらの1つ:
ちなみに 










