「機械学習」、「神経回路網」などの言葉の構造をよく耳にします。 これらの表現はすでに一般の人々の意識に入り、ほとんどの場合、パターンと音声認識、人間のようなテキストの生成に関連付けられています。 実際、機械学習アルゴリズムは、中小企業やオンライン出版物など、さまざまな種類のタスクを解決できます。 この記事では、スコアリングモデルの作成という実際のビジネス上の問題を解決できるニューラルネットワークの作成方法を説明します。 データの準備からモデルの作成とその品質の評価まで、すべての段階を考慮します。
記事で説明されている質問:
•モデルを構築するためのデータを収集および準備する方法。
•ニューラルネットワークとは何ですか。
•ニューラルネットワークをゼロから記述する方法
•利用可能なデータでニューラルネットワークを適切にトレーニングする方法
•モデルとその結果の解釈方法は?
•モデルの品質を正しく評価する方法は?
「コンピューターが考えることができるかどうかという問題は、もはや興味深いものではありません。
潜水艦が航行できるかどうかという質問よりも。」
エドガー・ウィーベ・ダイクストラ
多くの企業では、セールスマネージャーが潜在的な顧客と通信し、デモを行い、製品について話します。 彼らは、いわば、おそらく偶然に手に落ちた人々によって、100回目の魂をばらばらに引き裂かれます。 多くの場合、顧客は必要なもの、または製品が提供できるものを完全に理解していません。 そのようなクライアントとのコミュニケーションは、喜びも利益ももたらしません。 そして、最も不愉快なことは、時間制限のために、本当に重要なクライアントに十分な注意を払って取引を逃すことができないということです。
私は9月の分析サービスSerpstatの数学者プログラマーです。 最近、既存のスコアリングモデルと作業スコアリングモデルを改善し、販売の成功に影響する要因を再評価するという興味深いタスクを取得しました。 得点はお客様の調査に基づいて考慮され、各項目は質問への回答に応じて、合計得点に一定のポイントを与えました。 異なる質問に対するこれらすべてのポイントは、統計的仮説に基づいて配置されました。 スコアリングモデルが使用され、時間が経過し、データが収集され、ある日彼らが私のところに来ました。 これで十分なサンプルが得られたので、機械学習アルゴリズムを使用して安全に仮説を立てることができました。
スコアリングモデルの作成方法を説明します。 これは、実際のビジネスで発生したすべての困難と制限を伴う、実際のデータを使用した実際のケースです。 だから、まず最初に。
作業のすべての段階で詳しく説明します。
▸データ収集
▸前処理
modelモデルの構築
▸品質分析とモデルの解釈
デバイス、ニューラルネットワークの作成とトレーニングを検討してください。 このすべてを説明し、実際のスコアリングの問題を解決し、常に新しい理論を例で補強しています。
データ収集
最初に、将来のモデルでクライアント(またはオブジェクト)を表す問題を理解する必要があります。 さらなるプロセスがそれに基づいて構築されているため、タスクに真剣に取り組みます。 まず、オブジェクトを説明する重要な機能を見逃してはなりません。次に、機能を決定するための厳格な基準を作成します。 経験に基づいて、3つのカテゴリの質問を区別できます。
- ブール(2つのカテゴリ)、その答えはYesまたはNo(1または0)です。 たとえば、質問への答え:クライアントはアカウントを持っていますか?
- カテゴリー、特定のクラスに対する答え。 通常、3つ以上のクラス(マルチカテゴリ)があります。それ以外の場合は、質問をブールに減らすことができます。 たとえば、色:赤、緑、青。
- 量的、特定の指標を特徴付ける数字である答え。 たとえば、月あたりのヒット数:15。
なぜこのように詳細にこだわるのですか? 通常、機械学習アルゴリズムによって解決される古典的な問題を考えるとき、数値データのみを扱います。 たとえば、20 x 20ピクセルの画像からの白黒の手書き数字の認識。 この例では、400個の数字(黒と白のピクセルの明るさを表す)がサンプルの1つの例を表します。 一般に、データは数値である必要はありません。 実際、モデルを構築する際には、アルゴリズムが処理できる質問の種類を理解する必要があります。 たとえば、すべての種類の質問について決定木が訓練され、ニューラルネットワークは数値入力データのみを受け入れ、定量的属性についてのみ訓練されます。 これは、より良いモデルのためにいくつかの問題を放棄する必要があるということですか? データを正しく準備するだけで十分です。
データは次の古典的な構造を持つ必要があります。各i番目のクライアントの特徴ベクトルX (i) = {x (i) 1 、x (i) 2 、...、x (i) n }およびクラスY (i) -彼がそれを買ったかどうかを示すカテゴリ。 例:customer (3) = {green、bitter、4.14、yes}-買いました。
前述に基づいて、さらに準備するための質問のタイプを含むデータ形式を提示しようとします。
| クラス:
(カテゴリー) | 色:
(カテゴリー) | 味:
(カテゴリー) | 重さ:
(数) | 固体:
(ブール) |
|---|---|---|---|---|
| - | 赤 | 酸っぱい | 4.23 | はい |
| - | 緑色 | 苦い | 3.15 | いや |
| + | 緑色 | 苦い | 4.14 | はい |
| + | 青 | 甘い | 4.38 | いや |
| - | 緑色 | 塩辛い | 3.62 | いや |
表1-前処理前のトレーニングサンプルデータの例
前処理
データを収集したら、それらを準備する必要があります。 このステップは前処理と呼ばれます。 前処理の主なタスクは、モデルのトレーニングに適した形式でデータを表示することです。 前処理段階では、3つの主要なデータ操作があります。
- トレーニングサンプルの例が存在する標識のベクトル空間の作成。 本質的に、これはすべてのデータを数値形式に変換するプロセスです。 これにより、カテゴリ型、ブール型、およびその他の非数値型から私たちを救います。
- データの正規化。 たとえば、すべてのデータにわたる各特徴の平均値がゼロであり、分散が単位であるということを達成するプロセス。 データの正規化の最も典型的な例を次に示します。X =(X-μ)/σ
正規化関数def normalize(X): return (XX.mean())/X.std()
- ベクトル空間の次元を変更します。 フィーチャのベクトル空間が大きすぎる(数百万のフィーチャ)または小さすぎる(1ダース未満)場合、スペースの次元を増減する方法を適用できます。
ベクトル空間を構築する上で最も重要なトリックの1つは、カテゴリ型およびブール型の数の形式で表現する方法です。 会う: ワンホット (ロシア統一コード)。 このようなエンコーディングの主なアイデアは、カテゴリ属性を、可能なカテゴリの数に対応する次元を持つベクトル空間のベクトルとして提示することです。 この場合、このカテゴリの座標の値はユニットごとに取得され、他のすべての座標はリセットされます。 ブール値を使用すると、すべてが非常に単純になり、実際の単位またはゼロに変わります。
たとえば、サンプル項目は、苦い、甘い、塩辛い、酸っぱい、またはうま味(肉)のいずれかです。 ワンホットエンコードは次のようになります:bitter =(1、0、0、0、0)、sweet =(0、1、0、0、0)、salty =(0、0、1、0、0)、サワー=(0、0、0、0、1、0)、マインド=(0、0、0、0、0、1)。 なぜ4つのフレーバーではなく5つのフレーバーがあるのか疑問がある場合は、味覚感覚システムに関するこの記事を読んでください 。しかし、これはスコアリングとは関係ありません。4つを使用して、古い分類に限定します。
これで、カテゴリフィーチャを通常の数値ベクトルに変換する方法を学びました。これは非常に便利です。 データのすべての操作が完了したら、どのモデルにも適したトレーニングサンプルを取得します。 私たちの場合、ユニタリエンコーディングと正規化を適用すると、データは次のようになります。
| クラス: | 赤: | 緑: | 青: | 苦い: | 甘い: | サルティ: | 酸っぱい: | 重さ: | 固体: |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0.23 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | -0.85 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0.14 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0.38 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | -0.48 | 0 |
表2-前処理後のトレーニングサンプルデータの例
前処理とは、人間にとってはあまり便利ではないが機械が好む形式で理解できるデータを表示するプロセスであると言えます。
ほとんどの場合、スコアリング式は次の線形モデルです。
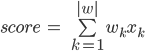
ここで、kは質問表の質問番号、w kは合計スコアリングのこのk番目の質問に対する回答の寄与係数です| w | -質問(または係数)の数、x k-この質問に対する答え。 さらに、質問は、ブール(yesまたはno、1または0)、数値(たとえば、身長= 175)、またはカテゴリカルですが、ユニタリーエンコーディングの形式(リストから緑:赤、緑、または青)で記述できます。 = [0、1、0])。 さらに、カテゴリ型の質問は、回答オプションのカテゴリと同じ数のブール型の質問に分類されると仮定できます(たとえば、クライアントの赤?クライアントの緑?クライアントの青?)。
モデル選択
今最も重要なこと:モデルの選択。 現在、スコアリングモデルを構築できる機械学習アルゴリズムには、ディシジョンツリー(決定木)、KNN(k最近傍法)、SVM(サポートベクトル法)、NN(ニューラルネットワーク)があります。 そして、モデルの選択は、私たちがそれから望むものに基づいているべきです。 まず、モデルの結果に影響を与えた決定がどれだけ明確である必要があります。 つまり、モデルの構造を解釈できることがどれほど重要かということです。
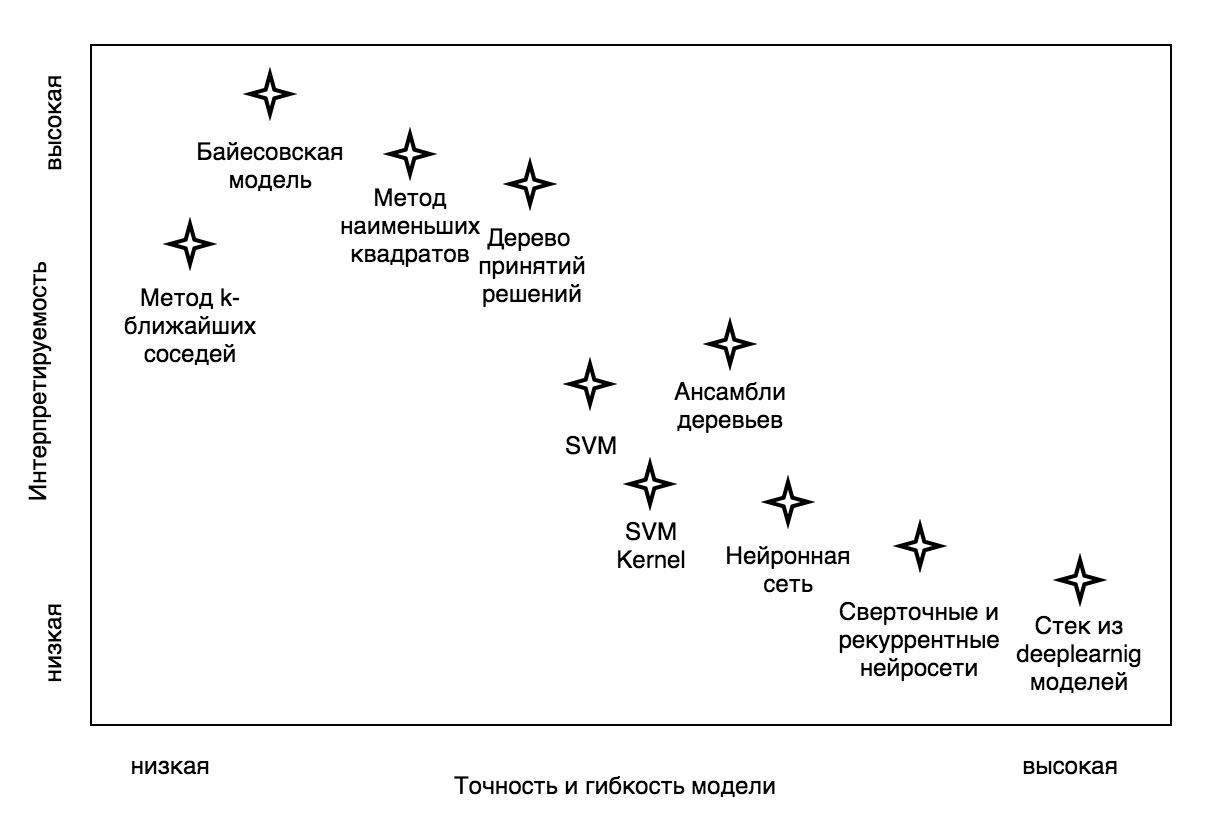
図 1-機械学習アルゴリズムの柔軟性と結果のモデルの解釈可能性の依存性
さらに、すべてのモデルが簡単に構築できるわけではなく、一部のモデルには非常に具体的なスキルと非常に強力なハードウェアが必要です。 しかし、最も重要なことは、構築されたモデルの実装です。 ビジネスプロセスが既に確立されており、複雑なモデルを導入することはまったく不可能です。 または、クライアントが質問に回答するときに、回答オプションに応じてプラスまたはマイナスのポイントを受け取る線形モデルが必要です。 場合によっては、逆に実装の可能性があり、入力パラメーターの非常に明白でない組み合わせを考慮に入れた複雑なモデルでさえ、それらの間の相互接続を見つけます。 それで、何を選ぶべきですか?
機械学習アルゴリズムを選択する際に、ニューラルネットワークに決めました。 なんで? まず、TensorFlow、Theanoなどの多くのクールなフレームワークがあります。 それらは、アーキテクチャと学習パラメータを非常に深く真剣にカスタマイズする機会を提供します。 第二に、モデルデバイスを、偶然にも十分に解釈される単層ニューラルネットワークから、数行のコードを変更するだけで、非線形の依存関係を見つける優れた能力を持つ多層ネットワークに変更する機能。 さらに、訓練された単層ニューラルネットワークは、さまざまなアンケートの質問への回答のポイントを加算する古典的な加法スコアリングモデルに変えることができますが、それについては後で詳しく説明します。
今少し理論。 ニューロン、活性化関数、損失関数、勾配降下、エラーバック伝播法などがネイティブワードである場合は、このすべてを安全にスキップできます。 そうでない場合は、短期間の人工ニューラルネットワークへようこそ。
人工ニューラルネットワークの短期コース
まず、人工ニューラルネットワーク(ANN)は、実際の生物学的ニューラルネットワーク(ANN)の組織の数学モデルです。 しかし、BNSの数学モデルとは異なり、ANNは、活動電位(PD)の「燃焼」の説明、神経伝達物質、イオンチャネル、二次中間体、輸送タンパク質などのすべての化学的および物理的プロセスの正確な説明を必要としません。実際のBNSの作業は、物理レベルではなく、機能レベルでのみです。
ニューラルネットワークの基本要素はニューロンです。 ニューロンの最も単純な機能的な数学モデルを作成してみましょう。 これを行うために、一般的な用語で生物学的ニューロンの機能を説明します。
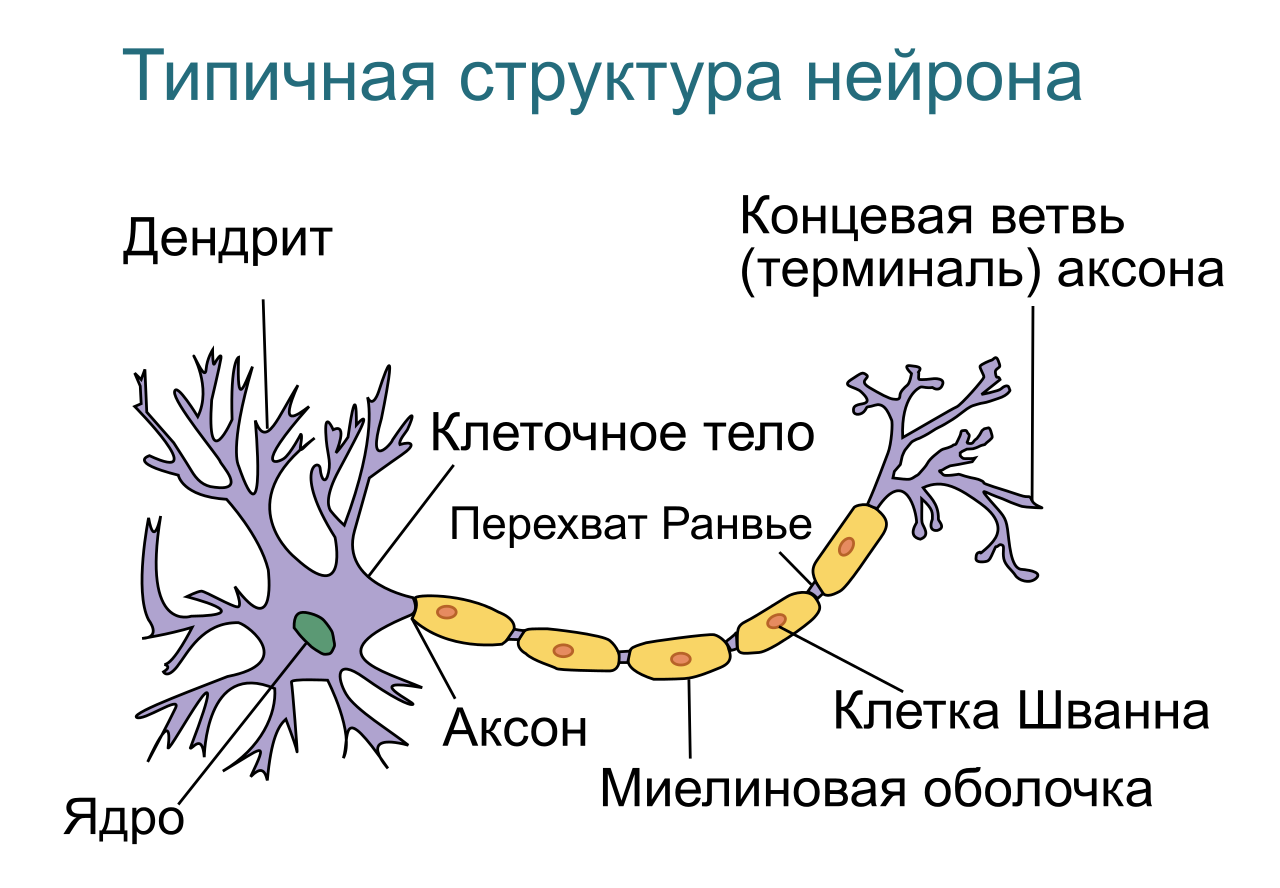
図 2-生体ニューロンの典型的な構造
ご覧のとおり、生体ニューロンの構造は、樹状突起、ニューロンの本体、および軸索に単純化できます。 樹状突起は、ニューロンへの入り口から情報を収集する分岐プロセスです(これは、受容体からの外部情報、たとえば色の場合は錐体から、または別のニューロンからの内部情報)。 着信情報がニューロンを活性化した場合(生物学的な場合、電位が特定のしきい値よりも高くなった)、励起波(AP)が生成され、ニューロンの体の膜を伝播し、神経伝達物質の放出を介して軸索を介して他の神経細胞に信号を送信します細胞または組織。
これに基づいて、ウォーレンマッカロックとウォルターピッツは1943年に数学的ニューロンモデルを提案しました。 そして、1958年、マッカロックピッツニューロンに基づいたフランクローゼンブラットがコンピュータープログラムを作成し、次に物理デバイス-パーセプトロンを作成しました。 これから、人工ニューラルネットワークの歴史が始まりました。 次に、ニューロンの構造モデルについて考えてみましょう。これについては、さらに対処します。

図 3-McCallock-Pitts数学ニューロンモデル
どこで:
- Xは入力パラメーターベクトルです。 ニューロンの入力になった数字のベクトル(列)(biol。さまざまな受容体の活性化の程度)。
Wは、重みのベクトル(一般的な場合、重みの行列)、学習プロセス中に変化する数値(biol。シナプス可塑性に基づくトレーニング、ニューロンはその受容体からの信号に正しく応答することを学習します)。 - 加算器は、対応する重みで乗算されたすべての入力パラメーターを加算するニューロンの機能ブロックです。
- ニューロンの活性化の機能は、加算器からの値に対するニューロンの出力の値の依存関係です。
- 次のニューロン。特定のニューロンの出力からの値が、独自の入力セットの1つに供給されます(このニューロンが最後のターミナルである場合、この層は存在しない場合があります)。
数学的ニューロンの実装
import numpy as np def neuron(x, w): z = np.dot(w, x) output = activation(z) return output
次に、これらの最小構造単位から、古典的な人工ニューラルネットワークが組み立てられます。 次の用語が採用されました。
- 入力(受容体)層は、パラメーター(属性)のベクトルです。 この層はニューロンで構成されていません。 これは、「外部」の世界からの受容体によって取得されたデジタル情報であると言えます。 私たちの場合、これは顧客情報です。 レイヤーには、入力パラメーターと同数の要素が含まれます(さらに、アクティブ化しきい値をシフトするために必要なバイアス項が含まれます)。
- 連想(非表示)レイヤーは、例を記憶し、複雑な相関関係と非線形依存関係を見つけ、抽象化と一般化を構築できる深い構造です。 一般的なケースでは、これはレイヤーではなく、入力と出力の間の多数のレイヤーです。 各レイヤーは、次のレイヤーのために新しい(より高いレベルの)特徴ベクトルを準備していると言えます。 高レベルの抽象化の学習プロセスにおける外観の原因は、この層です。 構造には、必要な数のニューロンと層が含まれ、存在しない場合もあります(線形分離可能セットの分類の場合)。
- 出力層は、各ニューロンが特定のクラスを担当する層です。 このレイヤーの出力は、異なるクラスに属するオブジェクトの確率分布の関数として解釈できます。 レイヤーには、トレーニングセットにあるクラスと同じ数のニューロンが含まれます。 2つのクラスがある場合、2つの出力ニューロンを使用するか、1つだけに制限することができます。 この場合、1つのニューロンは依然として1つのクラスのみを担当しますが、ゼロに近い値を生成する場合、そのロジックによるサンプリング要素は別のクラスに属している必要があります。
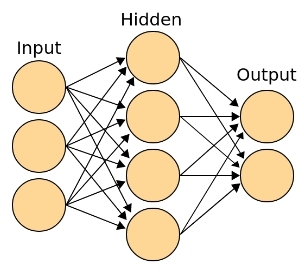
図 4-入力(受容体)、出力、クラス意思決定者、および連想(非表示)層を備えた古典的なニューラルネットワークトポロジ
隠された連想層の存在により、人工ニューラルネットワークは複雑な依存関係の発見に基づいて仮説を立てることができます。 たとえば、画像を認識する畳み込みニューラルネットワークの場合、画像ピクセルの輝度は入力層に送信され、出力層には特定のクラス(人間、機械、樹木、家など)を担当するニューロンが含まれます。隠れ層の「受容体」は、さまざまな傾斜角の直線から興奮し、角度、正方形、円、原始パターンに反応するニューロンを「特化」(特化)し始めます。 nt。 出力層の近くには、たとえば目、車輪、鼻、翼、葉、顔などに反応するニューロンがあります。

図 5-畳み込みニューラルネットワークの学習プロセスにおける階層的な関連付けの形成
生物学的アナロジーを引き出して、スピーチモデルに関する注目すべき神経生理学者Vyacheslav Albertovich Dubyninの言葉を参照したいと思います。
「私たちの脳は、下位レベルの単語を要約する単語を作成、生成できます。 バニー、ボール、キューブ、人形-おもちゃ、 おもちゃ、服、家具はオブジェクトです。 オブジェクト、家、人は環境のオブジェクトです。 そしてもう少し、私たちは抽象的な哲学的概念、数学的、物理的概念に到達します。 つまり、音声の一般化は、連合性頭頂皮質の非常に重要な特性であり、さらに、マルチレベルであり、外部世界全体の音声モデルを形作ることができます。 ある時点で、神経インパルスはこの音声モデルに沿って非常に活発に動くことができ、この動きを誇りに思う言葉「思考」と呼びます。
たくさんの理論?! しかし、良いニュースがあります。最も単純な場合、ニューラルネットワーク全体を単一のニューロンで表すことができます。 さらに、特にこれらのクラスのオブジェクトが線形に分離可能な空間内のオブジェクトのクラスを認識することになると、1つのニューロンでさえタスクに対処することがよくあります。 多くの場合、線形の分離可能性は、上記のように空間の次元を大きくすることで実現でき、1つのニューロンに限定されます。 ただし、ニューラルネットワークにいくつかの隠れ層を追加する方が簡単な場合があり、サンプルからの線形分離性は必要ありません。
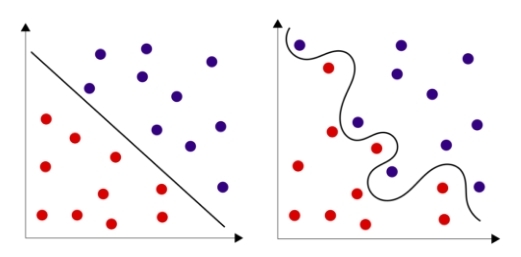
図 6-線形に分離可能なセットと線形に分離できないセット
それでは、このすべてを正式に説明しましょう。 ニューロンの入力には、パラメーターのベクトルがあります。 私たちの場合、これらは数値形式X (i) = {x (i) 1 、x (i) 2 、...、x (i) n }で表されるクライアント調査の結果です。 さらに、各クライアントはY (i) -リードの成功を特徴付けるクラス(1または0)に関連付けられています。 実際、ニューラルネットワークは、次元が特徴の数に対応するベクトル空間で最適な分離超曲面を見つけなければなりません。 この場合、ニューラルネットワークのトレーニングは、クラスを担当するニューロンが顧客が購入する場合に1に近い値を生成し、そうでない場合はゼロに近い値を生成する重み行列Wの値(係数)を見つけることです。
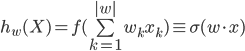
式からわかるように、ニューロンの仕事の結果は、入力パラメーターと学習プロセスで求められた係数の積の合計からの活性化関数(多くの場合で示される)です。 アクティベーション機能とは何かを見てみましょう。
任意の実数値がニューラルネットワークの入力になり、重み行列の係数も任意になる可能性があるため、それらの積の合計の結果は負から正の無限大までの任意の実数になります。 トレーニングセットの各要素には、このニューロンに関連するクラス値(0または1)があります。 0から1までの同じ範囲のニューロンから値を取得し、その値が近い場所に応じてクラスを決定することをお勧めします。 この値を、要素がこのクラスに属する確率として解釈するのがさらに良いです。 したがって、実数のセットの要素を0から1の領域にマッピングするような単調で滑らかな関数が必要です。 いわゆるシグモイドはこの位置に最適です。
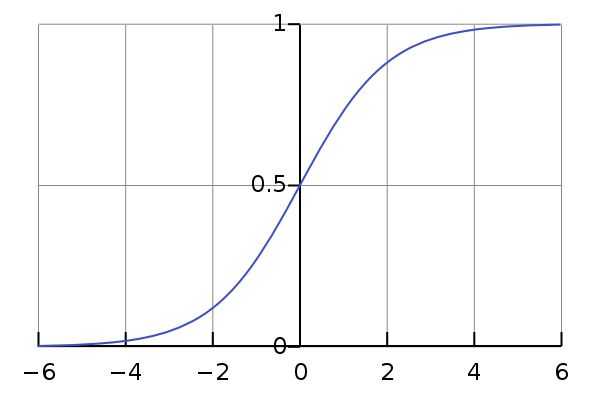
図 7-シグモイドクラスの最も古典的な代表の1つであるロジスティックカーブのグラフ
アクティベーション機能
def activation(z): return 1/(1+np.exp(-z))
ところで、実際の生体ニューロンでは、このような連続的な活性化機能は実現されていません。 私たちの細胞には、平均-70mVの静止電位があります。 ニューロンに情報が供給されると、活性化された受容体はそれと結合したイオンチャネルを開き、細胞内の電位の増加または減少につながります。 受容体の活性化にかかる反力と、トレーニング中に得られた重み行列の1つの係数との間に類似性を描くことができます。 電位が-50mVの値に達するとすぐにPDが発生し、興奮波は軸索に沿ってシナプス前端に到達し、神経伝達物質をシナプス間環境に投げ込みます。 つまり、実際の生物学的活性化は滑らかではなく段階的です。ニューロンは活性化されるかされません。 これは、モデルの構築において数学的に自由であることを示しています。 自然から分散コンピューティングと学習の基本原理を取り入れて、任意の特性を持つ要素で構成される計算グラフを構築できます。 この例では、ニューロンから離散値ではなく連続値を受け取ります。 一般的な場合、アクティベーション機能は異なる場合があります。
上記から学習する最も重要なことは次のとおりです。 「ニューラルネットワークトレーニング(シナプストレーニング)は、エラーを最小化するために重み行列の係数の最適な選択に減らす必要があります。」クラス。
ニューラルネットワークの作業の結果は、通常、仮説(英語の仮説)と呼ばれます。 h(X)で表し、オブジェクトの入力フィーチャ(パラメーター)に対する仮説の依存性を示します。 なぜ仮説なのか? これは歴史的に事実です。 個人的には、私はこの用語が好きです。 その結果、ニューラルネットワークの仮説を現実(オブジェクトの実際のクラス)に可能な限り対応させたいと考えています。 実際、ここでは経験から学ぶという主要なアイデアが生まれます。 ここで、ニューラルネットワークの品質を表す尺度が必要です。 この機能は、通常「損失機能」と呼ばれます。 通常、機能はJ(W)で示され、重み行列の係数への依存性を示します。 機能性が低いほど、ニューラルネットワークがミスを犯す可能性は低くなります。 この機能を最小限に抑えるためにトレーニングが行われます。 重み行列の係数に応じて、ニューラルネットワークの精度が異なる場合があります。 学習プロセスは損失汎関数の超曲面に沿った動きであり、その目的はこの関数を最小化することです。
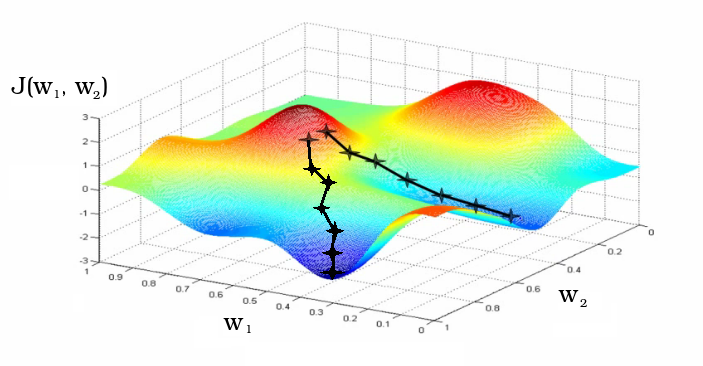
図 8-損失関数の極小値への勾配降下としての学習プロセス
通常、重み行列の係数はランダムに初期化されます。 学習プロセスでは、係数が変化します。 グラフは、近傍で初期化されたニューラルネットワークの重み行列の係数w 1およびw 2の変化として、2つの異なる反復学習パスを示しています。
次に、ニューラルネットワークのトレーニング方法について説明します。これには多くのオプションがありますが、2つについてお話します。進化的(遺伝的)アルゴリズムと勾配降下法です。これらの方法の両方が使用されます。進化アルゴリズムは、自然selectionのモデリングに基づいた人工知能の方向です。進化的教授法は非常に理解しやすく、初心者にとってはより良い方法です。現在では、主にニューラルネットワークの深層のトレーニングに使用されています。勾配降下法と誤差の逆伝播法はより複雑ですが、最も効果的で一般的な教育方法の1つです。
進化的学習
この方法の枠組みでは、次の用語を使用します:重み行列の係数-ゲノム、1つの係数-遺伝子、損失の「逆さまの損失」関数-フィットネスランドスケープ(ここでは、すでに局所最大値を探していますが、これは単なる慣習です)。この方法は本当に簡単です。ニューラルネットワークのトポロジ(デバイス)を選択したら、次のことを行う必要があります。
- -1〜1の範囲でランダムにゲノム(重み行列)を初期化します。これを数回繰り返して、異なるがランダムなニューラルネットワークの初期集団を作成します。母集団のサイズは、P-母集団または親によって示されます。
重み行列の係数のランダム初期化import random def generate_population(p, w_size): population = [] for i in range(p): model = [] for j in range(w_size + 1): # +1 for b (bias term) model.append(2 * random.random() - 1) # random initialization from -1 to 1 for b and w population.append(model) return np.array(population)
- . , - , () . : , -0.1 0.1.
def mutation(genom, t=0.5, m=0.1): mutant = [] for gen in genom: if random.random() <= t: gen += m*(2*random.random() -1) mutant.append(gen) return mutant
- , , ( — , — ). .
def accuracy(X, Y, model): A = 0 m = len(Y) for i, y in enumerate(Y): A += (1/m)*(y*(1 if neuron(X[i], model) >= 0.5 else 0)+(1-y)*(0 if neuron(X[i], model) >= 0.5 else 1)) return A
- « » P . 2, . : 80%.
def selection(offspring, population): offspring.sort() population = [kid[1] for kid in offspring[:len(population)]] return population
def evolution(population, X_in, Y, number_of_generations, children): for i in range(number_of_generations): X = [[1]+[v.tolist()] for v in X_in] offspring = [] for genom in population: for j in range(children): child = mutation(genom) child_loss = 1 - accuracy(X_in, Y, child) # or child_loss = binary_crossentropy(X, Y, child) is better offspring.append([child_loss, child]) population = selection(offspring, population) return population
そのような神経進化は改善することができます。たとえば、τは突然変異誘発率、μは突然変異誘発の強さなど、追加のパラメーター遺伝子を導入できます。これで、ニューロンの重みの行列に相加的な突然変異が確率τで導入され、選択した範囲(たとえば、-0.1から0.1)のμの各パラメーターに乱数が追加されます。これらの遺伝子も変動しやすいでしょう。
理想的には、選択は進化のさまざまな段階で変異誘発の強度と速度を制御し、フィットネスランドスケープの局所的な最大値から飛び出すことができるまでこれらのパラメーターを増やすか、ゆっくりと急激なジャンプなしにグローバルな最大値に移動するようにパラメーターを減らします。モデルに交差点を追加することもできます。これで、子孫は交配によって形成され、2つのランダムな親からランダムに半分の遺伝子を受け取ります。このスキームでは、ゲノムにランダムな突然変異の導入を残すことも必要です。
ここで、アレキサンダー・マルコフとエレナ・ナイマルクの本から引用するのが適切だと思います:
« — , — . , , — . , . , .»
次の資料を理解するのが難しい場合は、後で戻ってください。さらに、多くの機械学習ライブラリにより、この方法を使用して、詳細に立ち入らずにトレーニングを簡単に実装できます。電卓を使用してルートを抽出するとき、通常、彼がそれをどのように行うかについてはほとんど関心がなく、取得したいものを完全によく知っており、マシンに請求書を渡します。しかし、この方法に興味がある人のために、簡単に検討します。
まず、モデルの1つの出力ニューロンは1つのクラスのみを担当します。これがニューロンが担当するクラスのオブジェクトである場合、出力でそれを確認します。それ以外の場合はゼロを確認します。実際のクラス予測では、すでにわかっているように、人工ニューロンは0〜1のオープン範囲でアクティブになり、値はこれら2つの漸近線に任意に近づけることができます。これは、クラスをより正確に推測するほど、実際のクラスとこのクラスを担当するニューロンの活性化との間の絶対差が小さくなることを意味します。
ペナルティの数値を返す損失関数を作成してみましょう。ニューラルネットワークがクラス値に近い値を生成する場合は小さく、ニューラルネットワークがクラスの誤った定義につながる値を与える場合は非常に大きくなります。
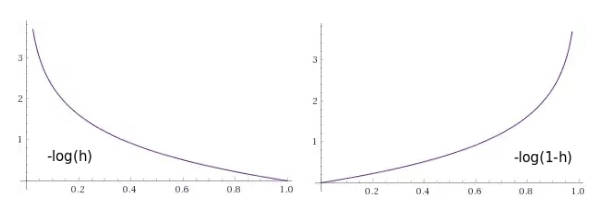
図 9-ニューロンの出力の関数としてのペナルティ関数のグラフ:1)オブジェクトがこのクラスに属する場合(1を期待する)、2)オブジェクトがこのクラスに属さない場合(ゼロを期待する)
ここで、損失関数を式として記述します。サイズmのトレーニングサンプルの各i番目の要素のYは常に0または1の値を取るため、2つの用語のうち1つだけが常に式に残ることを思い出してください。
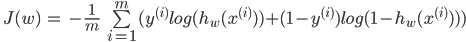
情報の理論に精通している人は、この表現でクロスエントロピーを認識します。情報理論の観点から見ると、学習とは、実際のクラスとモデル仮説の間の相互エントロピーを最小化することです。
損失関数
def binary_crossentropy(X, Y, model): # loss function J = 0 m = len(Y) for i, y in enumerate(Y): J += -(1/m)*(y*np.log(neuron(X[i], model))+(1.-y)*np.log(1.-neuron(X[i], model))) return J
重み行列の係数をランダムに初期化することで、モデルを改善する、つまり損失を減らすために、それらに変更を加えたいと思います。どのくらいの重量が損失関数に影響するかがわかっている場合、どれだけの重量を変更する必要があるかがわかります。ここで、偏微分-勾配-が役立ちます。関数が引数にどのように依存するかを示すのは彼女です。関数が1つの(極小)値だけ変化するように、いくつの(極小)量によって引数を変更する必要があるか。したがって、次のように重み行列を再初期化できます。
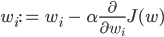
このステップを繰り返し繰り返します。実際、これは、損失関数の局所的最小値までの、αのサイズ(このパラメーターは学習率とも呼ばれます)の小さなステップでの緩やかな勾配降下です。言い換えると、Wの現在の値によって定義される各ポイントで、損失関数が最も速く変化する方向を見つけ、学習のダイナミクスはボールが局所的な最小値に徐々に転がるのに似ています。
勾配降下
def gradient_descent(model, X_in, Y, number_of_iteratons=500, learning_rate=0.1): X = [[1]+[v.tolist()] for v in X_in] m = len(Y) for it in range(number_of_iteratons): new_model = [] for j, w in enumerate(model): error = 0 for i, x in enumerate(X): error += (1/m) * (neuron(X[i], model) - Y[i]) * X[i][j] w_new = w - learning_rate * error new_model.append(w_new) model = new_model model_loss = binary_crossentropy(X, Y, model) return model
エラーの逆伝播法は、多層ニューラルネットワークの場合のこの推論の連鎖を継続します。彼のおかげで、勾配降下に基づいて深い層を訓練することが可能です。学習は、最後の層から最初の層まで段階的に行われます。この情報は、この方法の本質を理解するのに十分だと思います。
ニューラルネットワークトレーニングの例
1つのパラメーター-年齢に基づいて顧客の購入の確率を知りたいとします。購入の確率が50%を超える場合に興奮するニューロンを作成します。
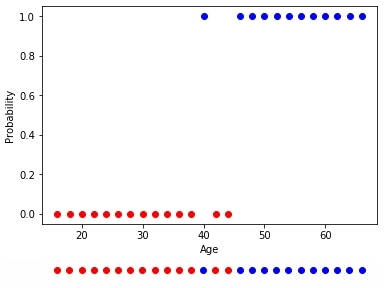
図 10-購入した人と購入しなかった人のトレーニングサンプル
したがって、ニューロンにはクライアントの年齢に関連する1つの受容体があります。さらに、シフト(またはオフセット)を担当する1つのバイアスメンバーを追加します。たとえば、これらのセットは線形に分離できませんが、おおよその境界、つまり、最高の分離超曲面(1次元の場合-ポイント)は、42歳でそれらの間に位置します。
ニューラルネットワークでは、42歳で0.5未満、高齢の顧客では0.5を超える購入の確率を与える必要があります。アクティベーション関数を呼び出すと、正の引数に対して0.5より大きい値を返し、負の引数に対して0.5より小さい値を返します。そのため、このアクティベーション関数をあるしきい値にシフトする機能が必要です。同時に、特徴ベクトルxの関数としての各ニューロンの励起の程度は重み行列の係数に依存し、したがって、そのような特徴ベクトルを持つ要素がこのクラスに属する確率に依存するため、トレーニングサンプルに最適な活性化関数のこのような破壊率が予想されます。
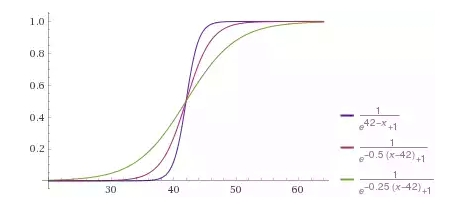
図 11-クライアントの年齢に対するニューロンの予想される応答。結果の「確信度」はさまざまで、引数の係数によって調整されます。
これを数学的に記述し、重みマトリックスにもう1つのバイアス項が必要な理由を理解します。関数f(x)を例えば42だけ右にシフトするには、引数f(x-42)から42を引く必要があります。同時に、例えば0.25を引数に掛けて次の関数f(0.25(x-24))を取得することにより、関数の弱い変曲を取得したいと思います。括弧を開くと、次のようになります。
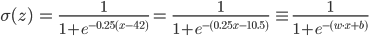
この場合、重み行列の望ましい係数はw = 0.25で、シフトはb = -10.5です。ただし、bが重み行列のゼロ係数(w 0 = b)であると仮定できます。たとえば、ゼロ記号が常に単一(x 0= 1)。次に、たとえば、x (15) = {x (15) 0、x (15) 1 } = [1、30]で表される45歳の15番目の「ベクトル化された」顧客は、68%の確率で購入できます。これらのすべての係数は、このような単純な例でも、「目で」把握するのは困難です。したがって、実際には、機械学習アルゴリズムに対するこれらのパラメーターの検索を信頼しています。この例では、重み行列の2つの係数(w 0 = bおよびw 1)を探しています。
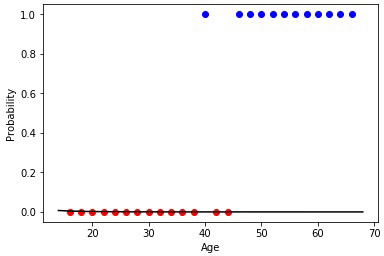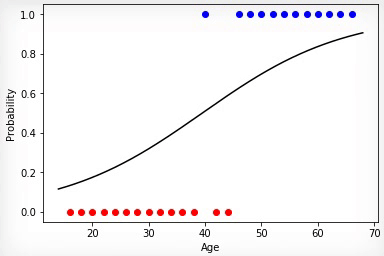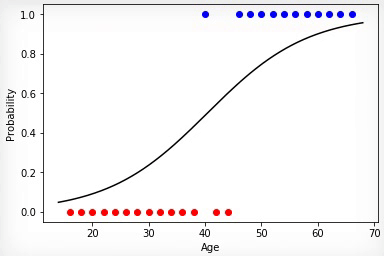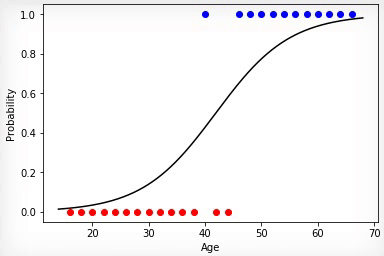
アニメーション1-正規化なしのデータの進化的学習
重み行列の係数をランダムに初期化し、進化アルゴリズムを使用することにより、100世代後に訓練されたニューラルネットワークを得ました。希望する学習成果をより速く、そのような急激なジャンプなしで取得するには、トレーニングの前にデータを正規化する必要があります。
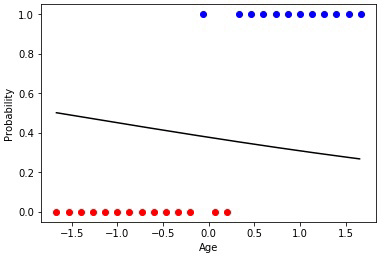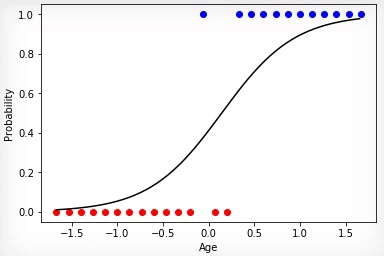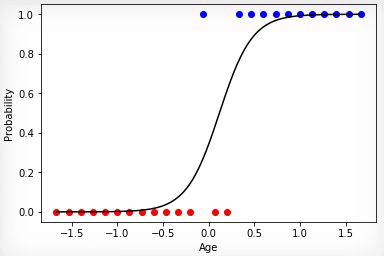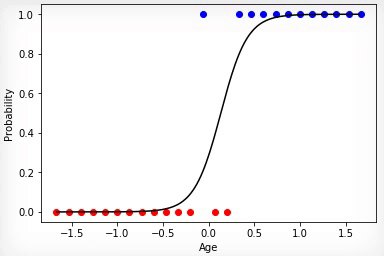
アニメーション2-正規化データの進化学習
勾配降下法は最も正確に機能します。この方法を使用する場合、データは常に正規化する必要があります。進化的アルゴリズムとは対照的に、勾配降下法は「突然変異」に関連するジャンプを経験しませんが、徐々に最適に移動します。しかし、マイナスは、このアルゴリズムが極小値にとどまり、それから抜け出せない、または勾配が実質的に「消失」して学習が停止する可能性があることです。
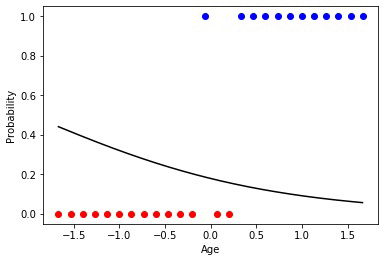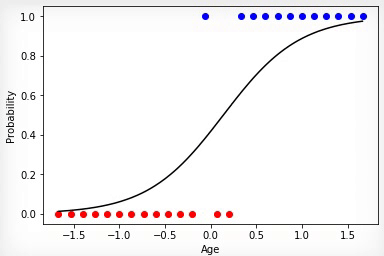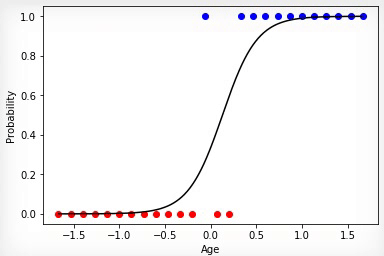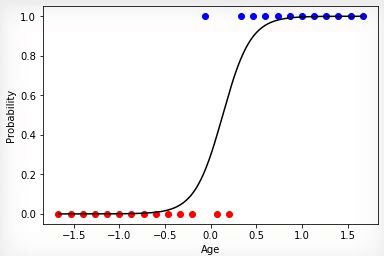
アニメーション3-勾配降下法に基づく学習
購入したクラスと購入していないクラスのセットが線形分離可能である場合、ニューロンはその決定により自信を持ち、その活性化の程度を変更すると、これらのセットの境界でより顕著な骨折が生じます。
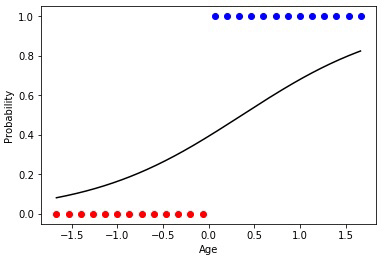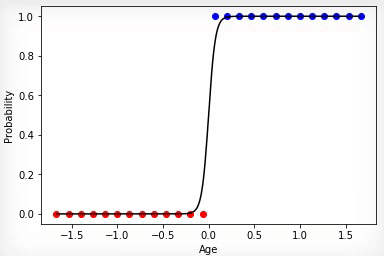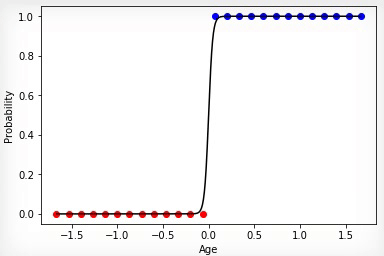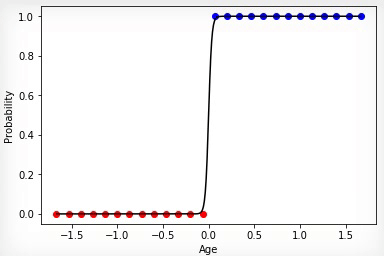
アニメーション4-線形分離可能セットの学習
上記に基づいて、以下を含む計算グラフの形式の古典的なニューラルネットワークを想像できます。
- 入力頂点x;
- 出力aの値を持つニューロンである頂点。
- バイアスbの原因となる頂点。
- 前の層の出力値に、重み行列wの対応する係数を掛けるエッジ。
- 仮説h w、b(x)は、最後の層の出力の結果です。
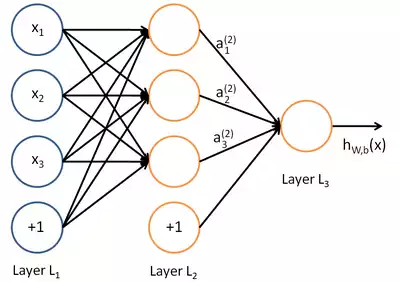
図 12-古典的な人工ニューラルネットワークのグラフの計算 TensorFlow
ライブラリのオンラインサンドボックスの例をいくつか考えてみましょう。すべての例で、オブジェクトが平面上にある2つのクラスを分離する必要があります。入力レイヤーには、横座標と縦座標に沿ったオブジェクトの座標に対応する値を持つ2つの「受容体」があります(さらに1つのバイアス、バイアスはアニメーションに表示されません)。前述のように、線形に分離可能なセットでトレーニングを行うには、出力ニューロンが1つだけあれば十分です。隠れた(連想的な)層はありません。学習は、逆伝播法に基づいています。アニメーション5-1つの出力ニューロンが分割線を見つける
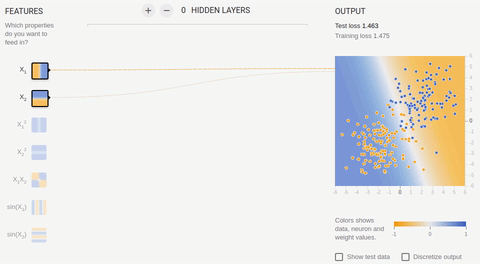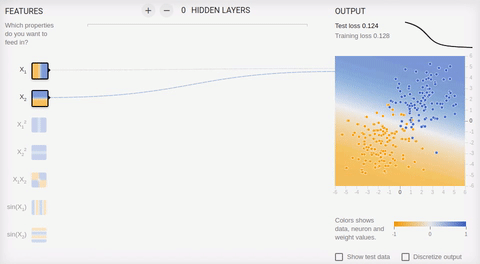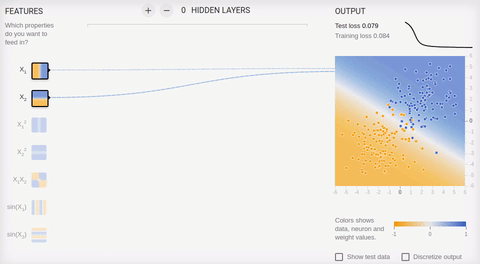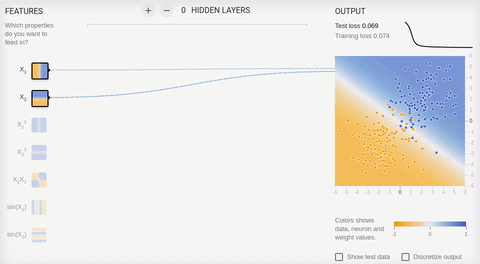
タスクを複雑にし、セットを分離してみましょう。最初の要素は両方の座標で正または負の値のみを持ち、2番目の要素は座標の1つの正と1つの負の値を持ちます。この例では、1つの分割線を省くことができないため、隠しレイヤーが必要です。最小限から始めて、隠れ層に2つのニューロンを追加してみましょう。
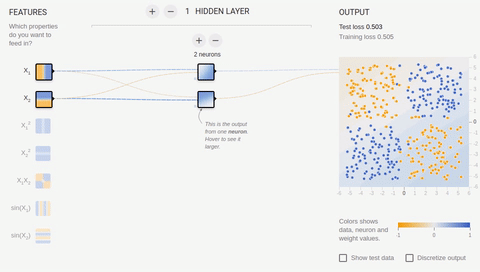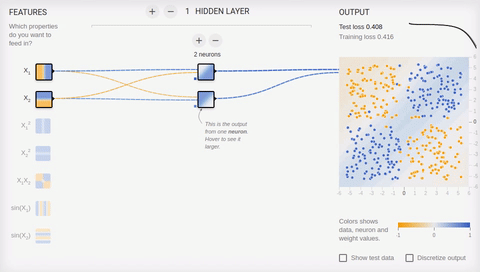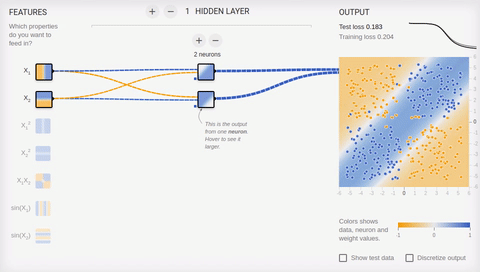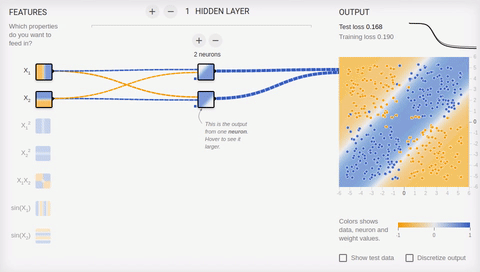
アニメーション6-2つの連想ニューロンと2つの分割線
ご覧のとおり、隠れ層の2つのニューロンはこのタスクに対応していますが、最良の方法ではありません。学習プロセスでニューロンの特殊化(分化)がどのように発生するかに注意してください。次に、4つのニューロンで構成される隠しレイヤーを作成します。

アニメーション7-4つの連想ニューロンと4つの分割線
ニューラルネットワークはこれをうまく処理しました。トレーニングの実施方法に注意してください。最初に、ニューラルネットワークは最も単純なソリューション-分割廊下を見つけました。その後、ニューロンの再専門化がありました。現在では、各非表示(連想)ニューロンがその狭いセグメントを担当しています。
かなり複雑な問題-異なるスパイラルアームにある2つのセットの要素の分離-を解決してみましょう。
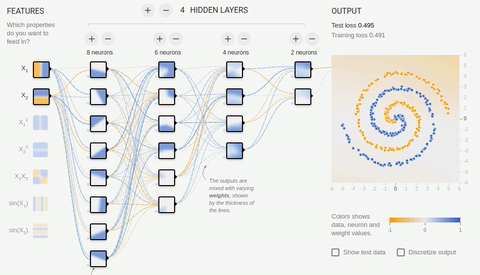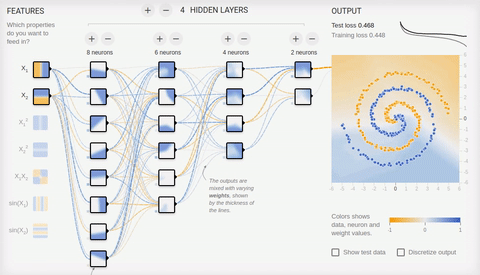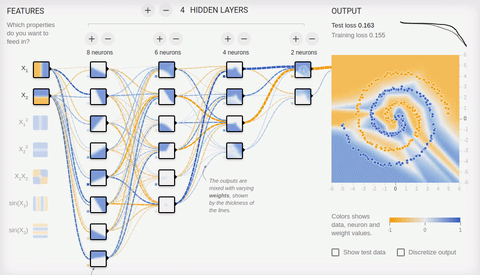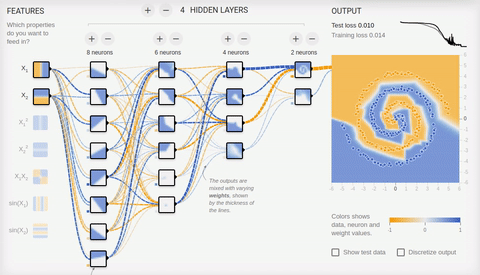
アニメーション8-ボトルネックトポロジを備えた多層ニューラルネットワーク
複雑な問題を解決するには、多くの隠れ層が必要です。ニューラルネットワークは、最初の隠れ層から最後の層までニューロンの数が減少するボトルネックトポロジにうまく対応します。連想ニューロンを特殊化するときに生じる複雑なパターンに注意してください。ディープニューラルネットワークの場合、隠れニューロンにはReLU(修正線形ユニット)アクティベーション関数を使用し、最後の層には通常のロジスティックアクティベーション(理想的にはソフトマックスアクティベーション)を使用することをお勧めします。
これで、人工神経回路網の超短期コースを終了し、知識を実践に移すことができると思います。あらゆるプログラミング言語で利用できるようになった既製のライブラリにモデルを構築し、この方向で理論的な知識を徐々に深めていくことをお勧めします。
モデルトレーニング
トレーニングサンプルと理論的知識の両方が得られたら、モデルのトレーニングを開始できます。ただし、問題は、セットの要素が不均等な比率で表示されることが多いことです。購入者は5%、非購入者は95%です。それではどうやって訓練しますか?結局のところ、誰も購入しないと主張することで、95%の信頼性を達成できます。
おそらく、この場合の精度メトリックは異なり、トレーニングも合理的である必要があります。これにより、ニューラルネットワークが同じ明らかに間違った結論を出さないようにします。このために、異なるクラスの同数の要素を含むトレーニング例でニューラルネットワークを「フィード」することを提案します。
たとえば、サンプルが20,000個しかなく、そのうち1,000個が購入している場合、各グループから500個のサンプルをランダムに選択し、トレーニングに使用できます。そして、この操作を何度も繰り返します。これは学習プロセスの実装を少し複雑にしますが、有能なモデルを得るのに役立ちます。
モデルとトレーニングアルゴリズムを選択したら、サンプルを部分に分割することをお勧めします。全体の70%を占めるトレーニングサンプルでトレーニングを行い、結果のモデルの品質を分析するために必要なテストサンプルに30%を寄付します。
モデル品質評価
モデルを準備したら、その品質を適切に評価する必要があります。 これを行うために、次の概念を紹介します。
- TP(真陽性)-真陽性。分類子は、顧客が購入することを決定し、彼は購入しました。
- FP(False Positive)-誤検知。分類子は顧客が購入することを決定しましたが、彼は購入しませんでした。これは、いわゆる第1種のエラーです。特に分類子が何らかの病気の検査である場合、第2種の間違いほど怖くはありません。
- FN(False Negative)-偽陰性。分類子は、クライアントは購入しないと決めましたが、購入する(または既に購入した)ことができます。これは、いわゆる第2種の間違いです。通常、モデルを作成するときは、2番目のエラーを最小限に抑え、それによって第1種のエラーを増加させることが望ましいです。
- TN(True Negative)-本当にネガティブ。分類子は、クライアントが購入しないと判断し、購入しませんでした。
パーセント信頼性の直接評価に加えて、上記のバイナリ分類結果に基づく精度(英語の精度)や完全性(英語の再現率)などのメトリックがあります。
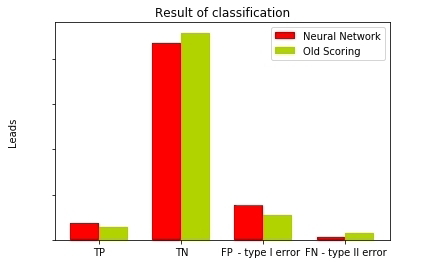
図 13-異なるモデルの分類結果の比較
ご覧のとおり、ニューラルネットワークは、以前のスコアリングモデルと比較して、第2種のエラーが3倍少なく、非常に優れています。確かに、潜在的な顧客を逃すと、潜在的な利益を逃します。ここで、利用可能なデータに基づいてモデルの品質指標を導き出しましょう。
信頼性指標
最も単純なメトリックは、精度メトリックです。しかし、すでにわかっているように、このメトリックはモデルの唯一のメトリックではありません。特に、サンプルにバイアスがある場合、つまり、異なるクラスの代表が異なる確率で出会う場合。
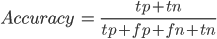
正確さと完全性
精度は、クラスのオブジェクトとして定義したすべてのオブジェクトに対する、クラスの正しく推測されたオブジェクトの比率を示します。たとえば、115を購入し、そのうち37を実際に購入することにしました。つまり、精度は0.33です。完全性(英語のリコール)は、クラスのすべての代表に対するクラスの正しく推測されたオブジェクトの比率を示します。たとえば、私たちの中で実際に購入したのは37個で、購入したのは43個だけだったため、フルネスは0.88です。
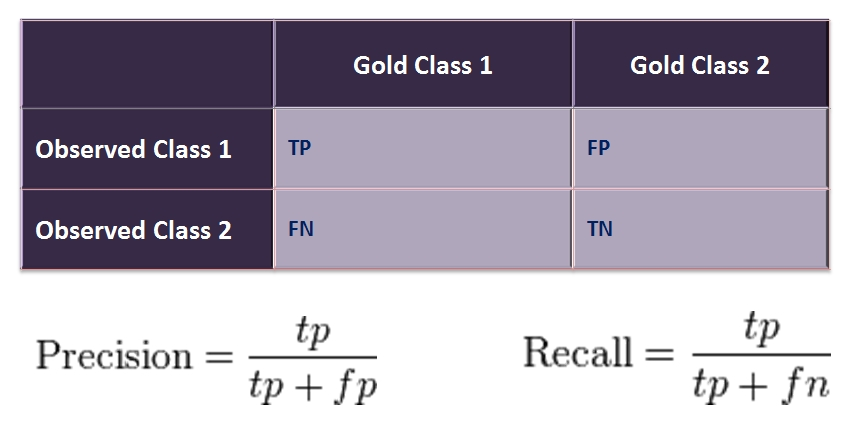
図 14-エラー表または混同マトリックス
Fメジャー
Fメジャー(Eng。F1スコア)もあります-高調波の精度と完全性の平均です。単一の数値測定を使用してモデルを比較するのに役立ちます。
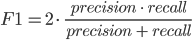
これらすべてのメトリックを使用して、モデルを評価します。
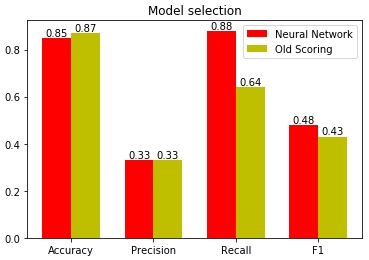
図 15-さまざまな統計指標に基づいたモデルの品質の評価
図からわかるように、モデルの品質の最大の偏りは完全性の指標に正確にあります(英語のリコール)。ニューラルネットワークは、潜在的な顧客の88%を推測し、わずか12%を逃しています。古いスコアリングモデルでは、潜在的な顧客の36%を逃し、マネージャーには64%しか渡されませんでした。それが実際に、スコアリングに影響を与えるさまざまな回答の重要度の係数を選択するようにニューラルネットワークを委任するほうがよい理由です。結局のところ、マシンはメモリ全体にサンプル全体を保持し、その中のパターンを見つけ、優れた予測能力を持つモデルを構築することができます。
モデルの解釈
既製のモデルがあれば、品質分析から得られた精度を期待して使用できます。複雑な(多層)モデルをプロセスに導入できる場合、それは適切ですが、そうでない場合は、単一層ニューラルネットワークから通常のスコアリングモデルを取得できます。このため、私たちは彼女のフードを大胆に調べるためにニューラルネットワークの構築に精通しています。
線形モデルのスコアリング式と1つのニューロン(または単層ニューラルネットワーク)の関数を比較します。
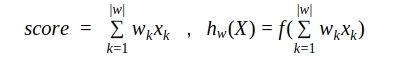
アクティベーション関数の引数である式は、線形スコア式と同一であることがわかります。したがって、単層ニューラルネットワークから重み行列の値を「プル」することにより、それらをスコアリングモデル係数として使用できます。現在のみ、これらの係数は、大量のデータに基づいてアルゴリズムによって慎重に選択されます。
次に、ニューラルネットワークの導入前後の係数に基づいて線形スコアリングの結果を比較します。ロジスティック活性化関数が値を与えることを思い出してください(ニューラルネットワークの観点から-購入した人々のクラスに属する確率)は、引数の正の値(重み行列に基づくスコア)で0.5を超えます。ポイントをスケーリングするために、ニューラルスコアリングの値に100を掛けて、しきい値として500を追加しました。古いスコアリングでは、しきい値は手動で選択され、合計で170になりました。これらはすべて、モデル自体に影響を与えない単なる線形操作です。
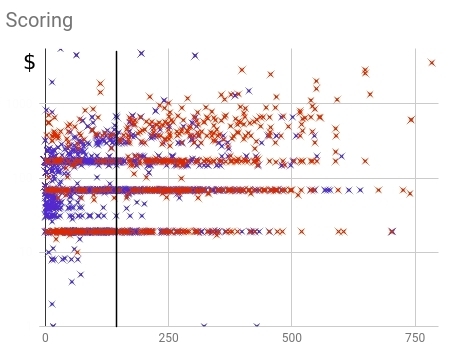
図 16-古いスコアリングモデル内で購入した(赤)および購入しなかった(青)
顧客の分布。分布からわかるように、顧客はスコア値の全範囲に広がりすぎています。完全性(購入した顧客の総数のモデルによって予測される割合)は64%です。
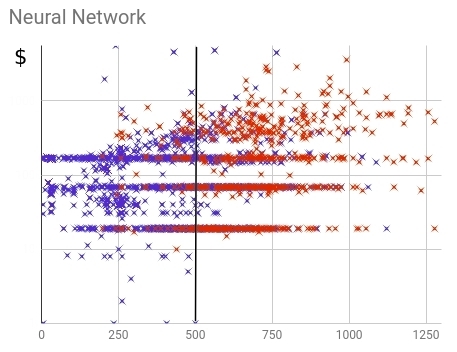
図 17-ニューラルスコアリングモデルのフレームワーク内で購入した(赤)および購入しなかった(青)顧客の分布。
分布から、ニューラルネットワークが古いモデルよりも購入したユーザーと購入しなかったユーザーを分離できたことがわかります。ほとんどの場合、購入しなかった人はしきい値未満の値を受け取り、購入した人は上記の値を受け取りました。完全性(購入した顧客の総数のモデルによって予測されるシェア)は88%です。
結果
問題を解決するために、関税を大量に購入する人たちにできるだけ多くの時間を費やしたかったのです。さらに、最も安いレートを購入した顧客が合格点を獲得しないスコアリングモデルを作成したいと考えました。
今回は、ニューラルネットワークをトレーニングするために、サンプルを一定以上の金額で購入した人のクラスと、低額で購入したかまったく購入しなかったクラスに分けました。
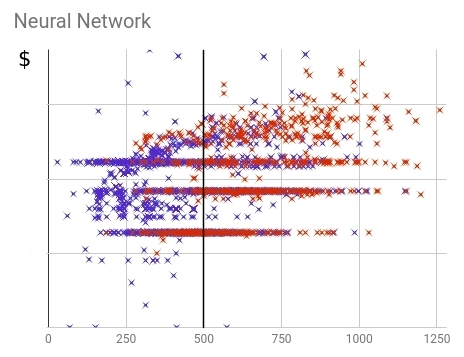
図 18-最終的なニューラルスコアリングモデル内での購入済み(赤)および未購入(青)の顧客の分布。
他のほぼ同等の精度インジケーターを使用して、ニューラルネットワークはより高い完全性を達成でき、高価な料金プランを購入した人の87%をカバーできました。比較のために:古いスコアリングは77%しか管理していません。これは、将来的に重要な潜在顧客の10%をカバーできることを意味します。同時に、得点の高い関税から高価な関税を購入した人の割合はほぼ同じです。ニューラルネットワークと古いモデルではそれぞれ23%と24%です。スコアリング値は購入金額とよく相関していることがわかります。
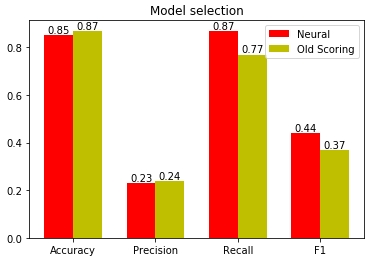
図 19-古いスコアリングモデルと新しいスコアリングモデルの品質の比較
この記事では、次のことを行います。
- データマイニングのすべての主要な段階を調べました。
- データの準備とトレーニングの両方で、多くの有用なテクニックを学びました。
- 古典的な人工ニューラルネットワークの理論に精通している。
- モデル品質の分析に対するさまざまな統計的アプローチを検討しました。
- 線形スコアリングモデルの構築例を使用して、ニューラルネットワークの作成から分析、実装までのすべての段階を説明しました。
- 最新の機械学習アルゴリズムが実際のビジネス上の問題の解決にどのように役立つかを示しました。
質問、提案、コメントがある場合は、コメントで議論しましょう。