これにより、システムはネットワークの参加者間の完全な信頼の欠如の状態で動作し、人的要因の影響は除外されます。
したがって、今日の記事では、ビットコインブロックチェーンの数学的基礎-楕円曲線、ECDSA、キーについてお話したいと思います。
 / HernánPiñeraCC BYの画像
/ HernánPiñeraCC BYの画像
ビットコインの基本的な部分は暗号化アルゴリズムです。 特に、ECDSAアルゴリズムは楕円曲線デジタル署名アルゴリズムであり、楕円曲線と有限フィールドを使用してデータに署名するため、第三者が署名の信頼性を確認できるため、改ざんの可能性がなくなります。 ECDSAは、いくつかの算術演算で構成される署名と検証に異なる手順を使用します。
楕円曲線
体K上の楕円曲線は、体Kの係数と「無限遠点」からなる3次方程式で定義される体Kの代数的閉包上の三次曲線です。 楕円曲線の1つの形式は、ワイエルシュトラス曲線です。
y²=x³+ ax + b
係数a = 0およびb = 7(ビットコインで使用)の場合、関数グラフは次の形式を取ります。
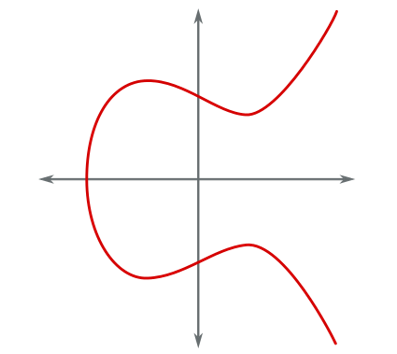
楕円曲線
楕円曲線にはいくつかの興味深い特性があります。たとえば、曲線上の2つの非接線ポイントと交差する非垂直線は、曲線上の3番目のポイントと交差します。 曲線 P + Q 上の2つの点の合計は 、点Rと呼ばれます。これは、X軸に対する点-R(直線(P; Q)を曲線との交点まで続けることによって構築される)の反射です。
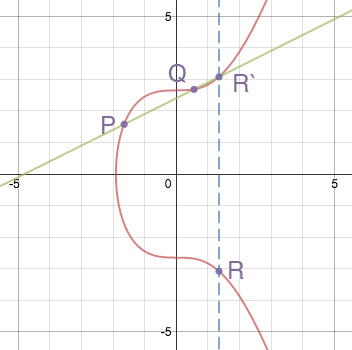
曲線上の2点の合計( ソース )
フォームP(a、b)とQ(a、-b)の座標を持つ2点を通る直線を描くと、縦座標軸に平行になります。 この場合、3番目の交差点はありません。 この問題を解決するために、いわゆる無限遠点が導入され、Oと表示されます。したがって、交差がない場合、方程式は次の形式P + Q = Oを取ります。
ポイントをそれ自体に追加する(2倍にする)場合、この場合、ポイントQへの接線が単純に描画され、得られた交点はX軸に関して対称に反映されます。
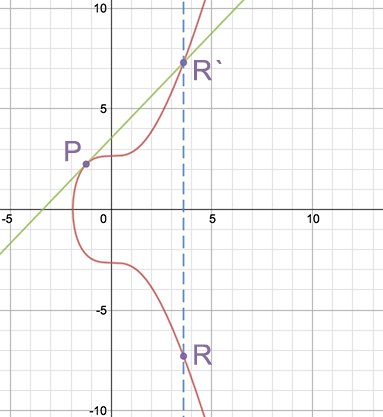
ダブリングポイント( ソース )
これらの操作により、ポイントR = k * Pのスカラー乗算が可能になり、ポイントPがk回追加されます。 ただし、大きな数値を処理するには、より高速な方法が使用されることに注意してください。
有限体上の楕円曲線
楕円暗号(ECC)では、同じ曲線が使用されますが、ある有限体でのみ考慮されます。 ECCのコンテキストでの最終フィールドは、各計算の結果が表示される定義済みの正数のセットとして表すことができます。
y²=x³+ ax + b(mod p)
たとえば、9 mod 7 = 2です。ここでは、0〜6の有限体があり、7を法とするすべての演算は、実行される数に関係なく、この範囲に入る結果になります。
この曲線のグラフは楕円曲線に似ていませんが、そのような関数の上記のプロパティ(加算、乗算、無限遠点)はすべて有効なままです。 67を法とする有限体で定義される楕円ビットコイン曲線、y²=x³+ 7は次のとおりです。

67を法とする有限体で定義されたビットコイン楕円曲線( ソース )
これは、すべてのx値とy値が0から66までの整数であるポイントのセットです。このグラフに描かれた直線は、バリア67に到達し、もう一方の端から続くとすぐにフィールドを「ラップ」します。 、同じ傾きを維持しますが、シフトします。 たとえば、この特定の場合のポイント(2、22)と(6、25)の追加は次のようになります。

ポイントの追加(2、22)および(6、25)( ソース )
他の楕円曲線がどのように見えるかを確認したい場合は、このサイトで実験できます 。
ビットコインのECDSA
ビットコインプロトコルには、楕円曲線とその最終フィールドのパラメーターセットが含まれているため、各ユーザーは厳密に定義された方程式セットを使用します。 固定パラメータの中では、曲線の方程式(方程式)、フィールドのモジュラスの値(素数のモジュロ)、曲線の基点(基点)、および基点の順序(順序)が区別されます。 基点の順序の計算については、 こちらをご覧ください 。 このパラメーターは特別に選択され、非常に大きな素数です。
bitcoinの場合、次の値が使用されます。
楕円曲線方程式:y²=x³+ 7
単純なモジュール:2 256-2 32-2 9-2 8-2 7-2 6-2 4-1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
基点:
04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
16進表記のX座標は太字です。 Y座標がすぐに続きます。
注文:FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
楕円曲線のこのパラメーターセットはsecp256k1として知られ、暗号化での使用が提案されているSEC(Standards for Efficient Cryptography)標準ファミリーの一部です。 ビットコインでは、secp256k1曲線はECDSA(楕円曲線デジタル署名アルゴリズム)と組み合わせて使用されます。 ECDSAでは、秘密鍵はユニットと注文値の間の乱数です。 公開鍵は 、秘密に基づいて形成されます。後者には、ベースポイントの値が乗算されます。 方程式の形式は次のとおりです。
公開鍵=秘密鍵* G
これは、シークレットキーの最大数(したがって、ビットコインアドレス)がもちろん順序に等しいことを示しています。 ただし、順序は非常に大きいため、別のユーザーの秘密キーをランダムにまたは意図的に取得するのは非現実的です。
公開鍵の計算は、ポイントの2倍化と追加の同じ操作を使用して実行されます。 これは、通常のパソコンやスマートフォンで数ミリ秒で解決できる些細な作業です。 しかし、逆問題(公開鍵から秘密鍵を取得する)は離散対数問題であり、計算的に複雑であると考えられます(ただし、この事実の厳密な証拠はありません)。 Ro Pollardなど、それを解決するための最もよく知られているアルゴリズムは、指数関数的な複雑さを持っています。 secp256k1の場合、問題を解決するには、約2,128の操作が必要です。通常のコンピューターでは、ユニバースの寿命に匹敵する計算時間を必要とします。
秘密/公開鍵のペアが受信されると、データの署名に使用できます。 このデータの長さは任意です。 通常、最初のステップは 、データをハッシュして、曲線のビット順序に等しいビット数を持つ一意の値を取得することです(256)。 ハッシュ後、zデータ署名アルゴリズムは次のとおりです。 ここで、Gは基点、nは順序、dは秘密キーです。
- 1からn-1の範囲の整数kを選択します
- 点(x、y)= k * Gはスカラー乗算を使用して計算されます
- r = x mod nを見つけます。 r = 0の場合、手順1に戻る
- s =(z + r * d)/ k mod nを見つけます。 s = 0の場合、ステップ1に戻ります
- 結果のペア(r、s)は署名です
データを受信して署名した後、公開鍵を知っている第三者はそれを検証できます。 署名を検証する手順は次のとおりです(Qは公開キーです)。
- rとsの両方が1〜n-1の範囲にあることを確認します
- w = s -1 mod nを計算します
- u = z * w mod nを計算します
- v = r * w mod nを計算します
- ポイント(x、y)= uG + vQが計算されます
- r = x mod nの場合、署名は正しいです。それ以外の場合は無効です
実際に
uG + vQ = u + vdG =(u + vd)G =(zs -1 + rds -1 )G =(z + rd)s -1 G = kG
最後の等式では、署名作成の段階でsの定義を使用します。
ECDSAセキュリティは、上記の秘密キー検索タスクの複雑さに関連しています。 さらに、元のスキームのセキュリティは、署名を作成するときのkの選択の「ランダム性」に依存します。 同じk値を複数回使用すると、PlayStation 3で発生した署名から秘密鍵を抽出できます。したがって、ほとんどのビットコインウォレットで使用されるものを含む最新のECDSA実装は、秘密鍵に基づいて決定的にkを生成し、署名されたメッセージ。
PS Bitfury Groupロシア( VkおよびFb) 。