Clever Geek Handbook

ヒルベルト曲線とZ次







すべての抜本的な曲線の意見を繰り返し聞いた。 空間インデックス付けに最も有望なのはヒルベルト曲線です。 これは、ギャップが含まれていないため、ある意味で「適切に配置されている」という事実に基づいています。 これは本当にそうであり、空間インデックス付けがそれと何を関係しているのか、それを理解してみましょう。



サイクルの最終記事：





ヒルベルト曲線には注目すべき特性があります-連続する2点間の距離は常に1に等しくなります（より正確には、現在のディテールのステップ）。 したがって、ヒルベルト曲線の値がそれほど大きくないデータは互いに遠くありません（ちなみに、反対は間違っています-モジェの隣接する点は値が大きく異なります）。 このプロパティのために、たとえば、





空間データに関しては、ヒルベルト曲線のプロパティはリンクの局所性を高め、DBMSキャッシュの有効性を高めることができます 。ここでは、計算値を含む列をテーブルに追加し、この列でソートすることをお勧めします。



空間検索では、ヒルベルト曲線がヒルベルトRツリーに存在します 。ここで、主なアイデア（非常に大まかに）-ページを2つの子孫に分割するときが来たら、ページ上のすべての要素を重心値でソートし、半分に分割します。



しかし、ヒルベルト曲線の別の特性に興味があります。これは自己相似のスイープ曲線です。 これにより、Bツリーに基づくインデックスで使用できます。 離散空間に番号を付ける方法について話している。

















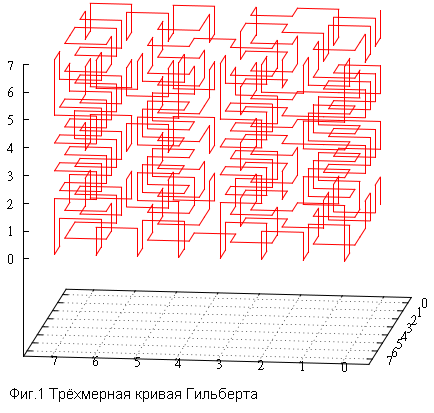
では、この直感的な感覚は、ヒルベルト曲線が空間インデックス付けに適しているということからどこで得られるのでしょうか？ はい、ギャップはありません;連続するポイント間の距離は、サンプリングステップに等しくなります。 それで何？ この事実と潜在的に高いパフォーマンスとの関係は何ですか？



最初に、ルールを策定しました。「適切な」番号付け方法により、インデックスページの全周が最小化されます。 私たちはBツリーのページについて話しているが、最終的にはデータになる。 つまり、インデックスのパフォーマンスは、読み取る必要があるページの数によって決まります。 参照サイズリクエストあたりの平均ページ数が少ないほど、（潜在的な）インデックスパフォーマンスが高くなります。



この観点から、ヒルベルト曲線は非常に有望に見えます。 しかし、この直感的な感覚をパンに塗ることはできないため、数値実験を実施します。











これは、グラフのように見える方法です。















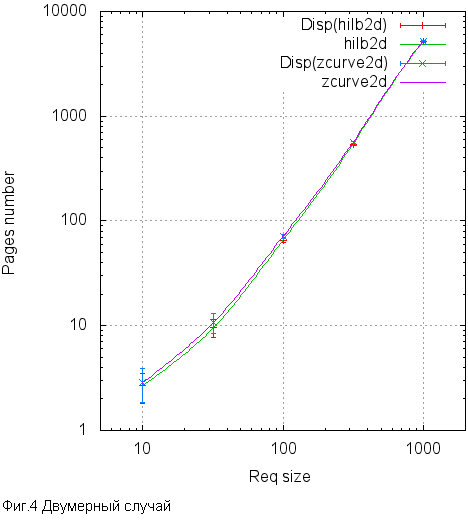
固定サイズのリクエストサイズ（2D 100X100）で、ページサイズに応じて読み取りページ数がどのように動作するかを確認するには、少なくとも好奇心から価値があります。













128、256、512のサイズに対応する、Zオーダーのよく見える「穴」。192、384、768の「穴」。それほど大きくはありません。



ご覧のとおり、差は10％に達する可能性がありますが、ほとんどどこでも統計誤差の範囲内です。 それにもかかわらず、ヒルベルト曲線はどこでもZ曲線よりも優れた動作をします。 それほどではないが、より良い。 明らかに、これらの10％は、ヒルベルト曲線に移動することによって達成できる潜在的な効果の上限推定値です。 ゲームはろうそくの価値がありますか？ 調べてみましょう。



実装。



空間検索でヒルベルト曲線を使用すると、多くの困難に直面します。 たとえば、3つの座標のキーの計算には（著者）約1000サイクルかかり、zcurveの場合の約20倍です。 おそらく、もっと効果的な方法があります。さらに、読み取りページ数を減らすことで、作業が複雑になると報われるという意見もあります。 すなわち ディスクはプロセッサよりも高価なリソースです。 したがって、主にバッファの読み取りに焦点を当て、時間にだけ注意します。



検索アルゴリズムについて。 要するに、それは2つのアイデアに基づいています-



  1. インデックスは、ページ分割されたBツリーです。 出力の最初の要素への対数アクセスが必要な場合は、バイナリ検索のような「分割統治」戦略を使用する必要があります。 すなわち 各反復でリクエストを平均してサブクエリに分割する必要があります。



    しかし、バイナリ検索とは対照的に、この場合、パーティションは破棄される要素の数を半分にするのではなく、幾何学的原理に従って発生します。



    スイープカーブの自己相似性から、原点から2のステップで伸びる正方（立方）格子を取る場合、この格子内の基本立方体には値の間隔が1つ含まれることになります。 したがって、検索クエリをこのラティスのノードに分析し、元の任意のサブクエリを連続した間隔に分割できます。 次に、これらの各間隔がツリーから減算されます。
  2. このプロセスが停止されていない場合、元の要求は1つの要素の間隔に削減されますが、これは望みではありません。 停止基準は次のとおりです。要求は、Bツリーの1ページに完全に収まるまでサブクエリに分割されます。 収まるとすぐに、ページ全体を読み、不要なものを除外するのが簡単になります。 何が合うのか調べる方法は？ サブクエリの最小ポイントと最大ポイント、およびページの現在のポイントと最後のポイントがあります。



    結局、サブクエリの処理の開始時に、サブクエリの最小ポイントをBツリーで検索し、検索が停止したシートページとその現在の位置を取得します。


これはすべて、ヒルベルト曲線とZオーダーでも同様に当てはまります。 ただし：





これにより、元のアルゴリズムを変更する必要が生じます。

まず、キーを操作するためのインターフェースが変更されました。





変更された検索アルゴリズムは次のようになります。



  1. サブクエリのキューを開始します。最初は、このキューには、 bitKey_limits_from_extentを呼び出して検出されたエクステント（および最小範囲キーと最大範囲キー）の要素が1つしかありません。
  2. キューが空ではない間：

    1. キューの先頭からアイテムを取得します
    2. bitKey_getAttrを使用して、それに関する情報を取得します
    3. baHasSmthがコックされていない場合、このサブクエリを無視します
    4. baSolidがコックされている場合、結果セットで直接値の範囲全体を減算し、次のサブクエリに進みます
    5. baReadReadyがコックされている場合、サブクエリの最小値をBツリーで検索します
    6. baReadReadyがコックされていない場合、またはこの要求に対して停止基準が機能しない場合（1ページに収まらない）

      1. サブクエリ範囲の最小値と最大値を計算します
      2. カットするキーのカテゴリを見つけます
      3. 2つのサブクエリを取得します
      4. それらをキューに入れ、最初に大きな値を持つもの、次に


エクステント[524000,0,484000 ... 525000,1000,485000]のリクエスト例について考えてみましょう。









これが、Zオーダーのリクエスト実行の様子です。

サブクエリ-生成されたすべてのサブクエリ、結果-見つかったポイント、

ルックアップ-Bツリーへのクエリ。









範囲は0x80000を超えているため、開始範囲はレイヤーの範囲全体のサイズです。 すべての最も興味深いものが中心に統合され、より詳細に検討します。









国境でのサブクエリの「クラスター」は注目に値します。 その発生のメカニズムはほぼ次のとおりです。たとえば、次のセクションは、検索範囲の範囲から幅3などの狭いストリップを切り取ります。さらに、このストリップにはドットさえありませんが、それはわかりません。 そして、サブクエリの範囲の最小値が検索範囲内にあるときのみチェックできます。 その結果、アルゴリズムはストリップをサイズ2と1のサブクエリに切り詰め、インデックスをクエリしてそこに何もないことを確認できます。 またはあります。



これは、読み取られるページの数には影響しません。Bツリーを通過するこのようなパスはすべてキャッシュに落ちますが、実行される作業量は印象的です。



さて、実際に読み取られたページ数と、それがどれくらいの時間を要したかを調べることは残っています。 次の値は、同じデータで、 以前と同じ方法で取得されました。 すなわち [0 ... 1 000 000、0 ... 0、0 ... 1 000 000]内の100 000 000のランダムポイント。



測定は2つのコアと4 GBのRAMを備えた控えめな仮想マシンで実行されたため、時間に絶対値はありませんが、読み取られたページ数は信頼できます。



ホットサーバーと仮想マシンでの2回目の実行で時間が表示されます。 読み取られたバッファーの数は、新しく生成されたサーバー上にあります。

NPoints Nreq 種類 時間（ミリ秒） 読みます ヒット数
1 100,000 zcurve

rtree

ヒルベルト 		.36

.38

.63 		1.13307

1.83092

1.16946 		3.89143

3.84164

88.9128
10 100,000 zcurve

rtree

ヒルベルト 		.38

.46

.80 		1.57692

2.73515

1.61474 		7.96261

4.35017

209.52
100 100,000 zcurve

rtree

ヒルベルト 		.48

.50 ... 7.1 *

1.4 		3.30305

6.2594

3.24432 		31.0239

4.9118

465.706
1,000 100,000 zcurve

rtree

ヒルベルト 		1.2

1.1 ... 16 *

3.8 		13.0646

24.38

11.761 		165.853

7.89025

1357.53
10,000 10,000 zcurve

rtree

ヒルベルト 		5.5

4.2 ... 135 *

14 		65.1069

150.579

59.229 		651.405

27.2181

4108.42
100,000 10,000 zcurve

rtree

ヒルベルト 		53.3

35 ... 1200 *

89 		442.628

1243.64

424.51 		2198.11

186.457

12807.4
1,000,000 1,000 zcurve

rtree

ヒルベルト 		390

300 ... 10000 *

545 		3629.49

11394

3491.37 		6792.26

3175.36

36245.5
どこで

Npoints-出力の平均ポイント数

Nreq-シリーズ内のクエリの数

タイプ -'zcurve'-内部構造を使用したハイパーキューブと数値解析を備えた固定アルゴリズム;; ' rtree '-要点のみの2D rtree。 ' hilbert 'はzcurveと同じアルゴリズムですが、ヒルベルト曲線では（*）-検索時間を比較するために、ページがキャッシュに収まるようにシリーズを10倍減らす必要がありました

時間 （ミリ秒）-平均クエリ実行時間

読み取り -要求ごとの読み取りの平均数。 最も重要な列。

共有ヒット -バッファーへのヒット数



*-値の広がりは、結果の不安定性が高いために発生します。必要なバッファがキャッシュ内に正常に存在した場合、大量のミスの場合は最初の数、2番目の数が観測されました。 実際、2番目の数値は宣言されたNreqの特性であり、最初の数値は5〜10倍小さくなります。



結論



ヒルベルト曲線の利点の「膝までの」評価が実際の状況のかなり正確な評価を与えたことは驚くにはあたらない。



出力のサイズがページサイズに匹敵するか、ページサイズより大きいクエリでは、キャッシュを超えるミス数でヒルベルト曲線の動作が改善されることがわかります。 ただし、ゲインは数パーセントです。



一方、ヒルベルト曲線の積分動作時間は、Z曲線の約2倍です。 著者が曲線を計算するための最も効率的な方法を選択しなかったと仮定します。たとえば、何かをより正確に行うことができます。 しかし、結局のところ、ヒルベルト曲線の計算はZ曲線よりも客観的に重くなります;それを操作するには、実際にかなり多くのアクションを実行する必要があります。 感じは、ページを読むことで数パーセントの利益でこの減速を取り戻すことは失敗するということです。



はい、非常に競争の激しい環境では、各ページの読み取りは数万の主要な計算よりも高価です。 しかし、ヒルベルト曲線上のキャッシュで成功したヒットの数は著しく多く、それらはシリアル化を経ており、競争環境で何か価値があります。



合計



したがって、Bツリー上に構築された自己相似スイープ曲線に基づく空間インデックスおよび/または多次元インデックスの可能性と機能に関する叙事詩は終わりました。



この間に（このようなインデックスが実現可能であるという事実に加えて）、この分野で伝統的に使用されているRツリーと比較して、





More articles:


All Articles