目次
前のパートでは、高次元の空間における低次元の基底の定義を検討し、基底空間に属さない頂点間の距離を決定する方法を示しました。 基底を置き換える場合、座標系のメトリックプロパティを保持するための要件も重要です。
基本行列
変換行列 (遷移行列)は通常、そのような行列を意味し、古い基底の要素(頂点)の座標に乗算すると、新しい基底の座標が取得されます。 これらの行列に基づいて、メトリックテンソルもある基底から別の基底に変換されます。
基底変換行列には、2つの基底の比較特性が含まれています。 これらの行列の中で、 不変行列は区別されます-値は基底の選択に依存しません。 たとえば、頂点間の距離行列は不変です。
直接遷移行列
初期ベース頂点のセットは次のように示されます (古い基準)、新しいセットとして (新しい基準)。 座標を変換するには、遷移行列を指定する必要があります-古い基底の新しい基底の頂点の座標の記述。 このような座標は、頂点の2座標または2座標のいずれかです。 二座標の遷移行列は次のように示されます 。 行列の行は、新しい基底の最上部の座標です 昔の 、それぞれ、列は新しい基準に対する古い基準の上部の2座標です。
遷移行列は正方である必要があります。したがって、頂点の座標だけでは十分ではありません-それらの数は座標成分の数よりも少ない(座標にスカラー成分が存在するため)。 したがって、法線ベクトル[0;の2座標を追加する必要があります。 1、1、... 1]。 次に、2座標の遷移行列の形状が主要なグラミアンに似たものになります。 行列を呼び出す リモート座標変換テンソル(DTP):
距離変換テンソルは不変です—値は基底に依存しません。 逆遷移(から に )与えられた行列の値は単純に転置されます(行と列が入れ替わります)。
事故は2座標であるため、ラプラシアン(LMT)を掛けると、2座標を取得できます。 。 遷移行列の双座標の構造:
この行列の最初の行は、法線の2座標です。 。
事故とは対照的に、遷移行列の2座標の値は、それらが取得される基礎(古いものと新しいもの)に依存します。 基底の選択により、LMTマトリックスが決まります。 明確にするために、基底の遷移の双座標 として示す 、そして基礎 どうやって 。 その後、次のアイデンティティが保持されます。 元の基準:
、
そして新しい:
、
ここに そして -初期基底のラプラシアンとグラミアン。 したがって そして -新しい基底のメトリックテンソル。
ある基底から別の基底に渡すとき、変換行列が与えられている場合、新しい基底の計量テンソルを決定する必要があります。
逆遷移行列
遷移行列 そして 遷移行列の行列式がゼロ以外であれば可逆です:
または
変換行列のゼロ行列式は、基底の直交性を意味します。 直交基底では、投影メトリックを表現することは不可能です。 非直交ベースを検討します。 次に、逆遷移行列は次のように直線で表されます。
マトリックス -古い基底の頂点の双座標を表します 新しいのピークに対して 。 つまり、双座標を反転すると、相互の双座標が得られます。
マトリックス ラプラス基底変換テンソル(LTP)です。 その構造は、ラプラシアン(LMT)の構造に似ています。
ここに主要なマイナーがあります 対称ラプラシアンです。 境界では、2つのベース(シンプレックス)のオルソセンターの逆投影の重心座標。 初期基底のオルソセンターは、新しいの重心座標で表されます- 、および元の座標の新しいのオルソセンター- 。
「逆投影」の意味を以下に説明します。
ラプラステンソルの隅にあるのはスカラーです 。 その値は、新しいベースと古いベースの2つのベースのスカラー積を反映しています。 その意味を明らかにするために、2つの状況を検討します。1)塩基が同じ空間に属し、2)塩基が異なる空間に属します。
1つの空間の基底のスカラー積
一般的な空間では、基底のスカラー積はオルソセンターのノルム( そして )およびオルソセンター間の距離( ):
この式は、共通の頂点(3.8)を持つペアのスカラー積の式に似ています。 したがって、関係(5.5)をオルソセンターのスカラー積の定義と見なすことができます。
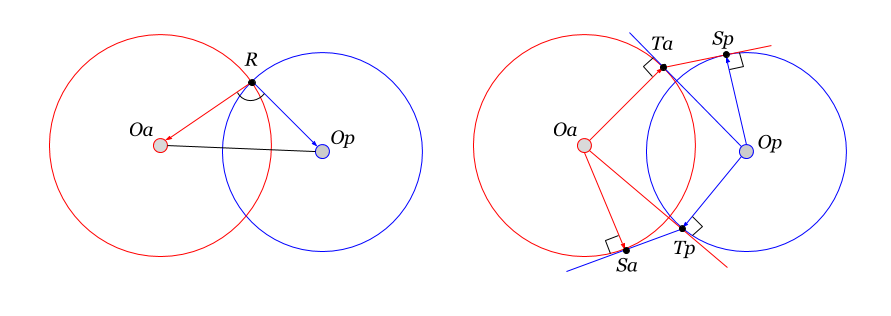
この図は、オルソセンター(円)のスカラー積の幾何学的解釈を示しています。 左-隣接ペアのスカラー積による定義 そして 。 円が交差する場合、共通の要素があります -ペアの隣接要素。
要素のスカラー積は、 相互の度合い (右の図を参照)によって決定できます。 ポイントの次数の幾何学的定義は、第2部に記載されています。 (2.9)によると、ポイントの程度 要素からの相対は、点から要素までの距離で表されます および要素の割合 :
ポイントの代わりに別の要素を使用する場合、この定義を一般化できます。 次に、2つの要素の相互度合い そして 次のスカラー量です :
この式はDarbouxの積として知られています 。 右の図は、ポイントの構成を示しています。ポイント間の距離は、要素の相互度合いに等しくなります。
その特性によれば、要素の相互の程度は、点の程度の特性を一般化します。つまり、それらの相対的な位置を決定します。 要素が互いに外側にある場合、相互の度合いは正であり、交差する場合は負です。 交差点とは、接触点がある状況を意味します (または )要素内にある (または それぞれ)(図では、要素の相互の程度は正です)。
この場合、スカラー積(5.5)は要素の相互半次(およびその逆)です。 (2.10)半次数は(-2)で割った累乗であることを思い出してください。
要素の中心が一致する場合( )、そのスカラー積は平均ノルムに等しくなります:
異なる空間の基底のスカラー積
基底が異なる空間に属する場合、それらのスカラー積の幾何学的解釈 複雑です。 まず、代数的アイデンティティを与えます。 それらは最初の部分で与えられたラプラステンソルの成分のためのそれらと同様です。
基底のスカラー積は、距離遷移行列の行列式とその主なマイナーの比を通して表現できます(5.1.1を参照)。
基点の相互基準と、それらのオルソセンターの逆投影の重心座標の関係:
-基底の頂点用 。
-基底の頂点用 。
点の逆投影が何であるかを把握しましょう。 ポイントがあるとしましょう 基礎に属する 。 次に、基底への逆投影 そのような点があるでしょう 垂線がそこから基底部に落ちたこと 出発点で彼と交差する 。
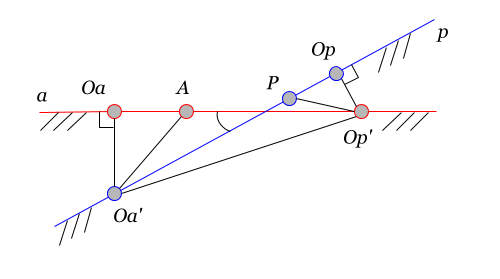
図では、点の逆投影 宇宙へ ポイントです 、およびポイントの逆投影 宇宙へ -ポイント 。 ポイント そして 基地のオルソセンター そして それに応じて。
逆投影の概念は、要素ノルムにも適用されます。 背面投影のノルムは、元の投影よりも大きくなります(直接投影とは対照的)。 表示距離 基準のオルソセンターの基準は 。 基底への逆投影 距離があります:
。
したがって、基底ノルムの逆投影 基づいて 距離があります
。
中心の逆投影間の距離を 、異なる空間の基底のスカラー積について次の式を取得します。
私たちは、それが1つの空間の底の相互ノルムと一致する形で見ることができます(5.5)が、距離の代わりに、相互基底への逆投影が使用されます。 基底が1つのスペースに属する場合、スペース間の角度はゼロになり、式(5.9)は(5.5)になります。
上記の式はすべて、グラフ空間にも適用できます。 グラフには、記述された球体(基底)はありませんが、接続性はあります。 次に、グラフのベースのスカラー積は、相互接続性を反映する必要があります。
新しい基礎の計算
ここでは、2つの状況も考慮します。1)新しいベースと古いベースが同じスペースに属し、2)異なるスペースに属します。 最初のケースは、原則として、通常の幾何学的空間を指します(基底を変更するとき、そのスペースはめったに変化しません)、2番目のケースはグラフの空間を指します。
要素(頂点)が基底空間に属しているかどうかは、与えられた空間のノルムによって判断できます。 ゼロに等しい場合、要素はスペースに属します。
単一基底空間
新しい基底のグラミアンを取得するには 新しい基底の要素の二座標を乗算する必要があります 双座標へ 。 結果の行列は、新しい基底のスカラー積の行列になります ( 前の部分の 4.4.2を参照)。 したがって、基底空間が一致する場合、古い基底に対する新しい基底の頂点のノルム行列は、新しい基底のグラミアンになります。
このグラミアンにストロークを付けて、一般的な基底空間の状態を記憶しました。 新しい基底のラプラシアン(LMT)は、グラミアン(DMT)を逆にすることで取得できます。
新しい基底の要素の座標は、古い行列と遷移行列の座標で表現できます。 二座標 :
新しい基底の要素の双座標 :
上記の式はすべて、通常の(ベクトル)座標系の座標変更式に似ています。 共通空間内で、ポイントベースを使用することは、ベクトルベースを使用することに似ています。
ベースライン変換の例
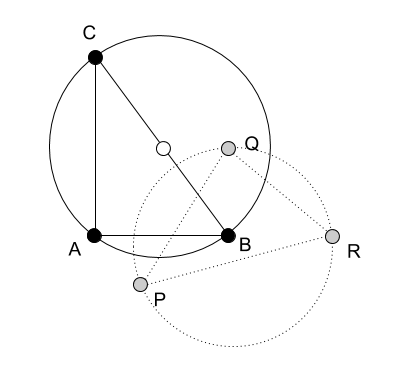
KDPVは主な基盤を示しています 3つの頂点( A、B、C )と新しい基底 頂点( P、Q、R )によって形成されます。 メインベースのDMTの値は最初の記事にあります :
\ begin {array} {c | cccc}
Gm_ {aa}&*&A&B&C \\
\ hline
*&0&1&1&1 \\
A&1&0&-4.5&-8 \\
B&1&-4.5&0&-12.5 \\
C&1&-8&-12.5&0 \\
\ end {array}
アスタリスクは、スカラーコンポーネントを示します。 ラプラシアン(LMT)の値は、グラミアン(DMT)を逆にすることで取得できます。
与えられたリモート遷移行列を考慮します。 彼女の見解:
\ begin {array} {c | cccc}
Dm_ {pa}&*&A&B&C \\
\ hline
*&0&1&1&1 \\
P&1&-1.0&-2.5&-13.0 \\
Q&1&-6.5&-2.0&-6.5 \\
R&1&-12.5&-2.0&-20.5 \\
\ end {array}
遷移行列の二座標値は、式(5.2.1)によって取得されます。
\ begin {array} {c | cccc}
Ba_p {} ^ a&*&A&B&C \\
\ hline
*&1&0&0&0 \\
P&-1.5&0.91(6)&0.(3)&-0.25 \\
Q&2.0&-0.5&1.0&0.50 \\
R&-5.0&-0。(6)&1.(6)&0.0 \\
\ end {array}
双座標のスカラー成分(最初の列の値)は軌道です。 重心成分の合計は1です。
ラプラス変換テンソル(5.3.1):
\ begin {array} {c | cccc}
Lt ^ {ap}&*&P&Q&R \\
\ hline
*&2.15&0.30&1.15&-0.45 \\
A&0.058(3)&0.11(6)&-0.0(6)&-0.05 \\
B&0.9(6)&-0.0(6)&-0.0(3)&0.10 \\
C&-0.025&-0.05&0.10&-0.05 \\
\ end {array}
ベクトル 新しい基底( PQR )の頂点に対する古い基底( ABCシンプレックス)のオルソセンターの重心座標です。 したがって、ベクトル -逆に、古い基底の頂点に対するシンプレックスPQRのオルソセンターの重心座標。
(5.10.1)を使用して、新しい基底のグラミアンを取得します。
\ begin {array} {c | cccc}
Gm '_ {pp}&*&P&Q&R \\
\ hline
*&0&1&1&1 \\
P&1&0&-6.5&-8.5 \\
Q&1&-6.5&0&-4.0 \\
R&1&-8.5&-4.0&0 \\
\ end {array}
\ begin {array} {c | cccc}
Gm_ {aa}&*&A&B&C \\
\ hline
*&0&1&1&1 \\
A&1&0&-4.5&-8 \\
B&1&-4.5&0&-12.5 \\
C&1&-8&-12.5&0 \\
\ end {array}
アスタリスクは、スカラーコンポーネントを示します。 ラプラシアン(LMT)の値は、グラミアン(DMT)を逆にすることで取得できます。
与えられたリモート遷移行列を考慮します。 彼女の見解:
\ begin {array} {c | cccc}
Dm_ {pa}&*&A&B&C \\
\ hline
*&0&1&1&1 \\
P&1&-1.0&-2.5&-13.0 \\
Q&1&-6.5&-2.0&-6.5 \\
R&1&-12.5&-2.0&-20.5 \\
\ end {array}
遷移行列の二座標値は、式(5.2.1)によって取得されます。
\ begin {array} {c | cccc}
Ba_p {} ^ a&*&A&B&C \\
\ hline
*&1&0&0&0 \\
P&-1.5&0.91(6)&0.(3)&-0.25 \\
Q&2.0&-0.5&1.0&0.50 \\
R&-5.0&-0。(6)&1.(6)&0.0 \\
\ end {array}
双座標のスカラー成分(最初の列の値)は軌道です。 重心成分の合計は1です。
ラプラス変換テンソル(5.3.1):
\ begin {array} {c | cccc}
Lt ^ {ap}&*&P&Q&R \\
\ hline
*&2.15&0.30&1.15&-0.45 \\
A&0.058(3)&0.11(6)&-0.0(6)&-0.05 \\
B&0.9(6)&-0.0(6)&-0.0(3)&0.10 \\
C&-0.025&-0.05&0.10&-0.05 \\
\ end {array}
ベクトル 新しい基底( PQR )の頂点に対する古い基底( ABCシンプレックス)のオルソセンターの重心座標です。 したがって、ベクトル -逆に、古い基底の頂点に対するシンプレックスPQRのオルソセンターの重心座標。
(5.10.1)を使用して、新しい基底のグラミアンを取得します。
\ begin {array} {c | cccc}
Gm '_ {pp}&*&P&Q&R \\
\ hline
*&0&1&1&1 \\
P&1&0&-6.5&-8.5 \\
Q&1&-6.5&0&-4.0 \\
R&1&-8.5&-4.0&0 \\
\ end {array}
異なるスペースの拠点
ベースが異なるスペースにある場合、式(5.10.1)は、新しいベースの頂点間の半距離の誤った値を与えます。 前の部分では、一般的な場合、頂点間の正しい距離を見つけるために、基本行列を標準行列に追加する必要があることが示されました (4.5):
したがって、基底を別の空間の基底に変換する場合、遷移行列とともに、新しい基底の基本行列(元の相対行列)を指定する必要があります。
基本行列を定義するには、その幾何学的な意味を思い出すと便利です( 4.6.1を参照)。 基本行列の要素は、基底空間への投影から頂点に向けられた法線のスカラー積です。 共通のスーパースペースの特定の(しかし実際には重要な)場合、基本行列の要素は、与えられた要素から基底空間までの距離の積として計算されます。
逆投影のスカラー積
グラフ空間では、基本行列の値は、古い基底と新しい基底の間の隣接行列から取得できます。 。 この行列の要素は、2つのベースの頂点間の結合の重みです。 マトリックスが既知であり、可逆である場合、逆隣接マトリックスを取得できます。
結果のマトリックス(および隣接マトリックス)は不変です。その値は基底の選択に依存しません。 行列要素の値 2つのベースの頂点間の逆投影のスカラー積を反映します。 図は説明図を示しています。
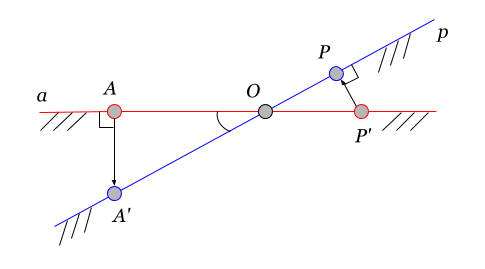
ここで、点Aは基底に属します 、および基底への点P 。 ダッシュは、隣接ベースのポイントの逆投影を示します。 その場合、行列要素の値はベクトルのスカラー積です そして :
この関係は、頂点から空間の交点の超平面までの距離(図の点O )と空間間の角度で表すことができます。 :
式(5.13.2 ')から、ベースが直交している場合、 、スカラー積の要素は無限大になります。
最終基底変換式
投影のスカラー積の行列の次元を減らすと便利です 残りの遷移行列の次元に合わせて、ゼロで囲みます。 次に、基底の基本行列 として定義される
すべてを組み合わせて、新しい基底のグラミアンの最終式を取得します :
初期基底は、与えられた変換行列に対して対称的に表現されます:
ここに そして -遷移行列(5.2.1)および(5.2.2)の2座標。 -合計距離変換マトリックス:
この行列は不変であり、2つの部分で構成されます-リモート変換テンソル 基底空間の非共平面性に関連する添加物-投影のスカラー積の行列 。
ラプラス基底テンソルは、DMTの逆数(5.15)によって取得されます。 塩基の接続を決定する問題は解決されました。
まとめると。 シリーズ全体の重い定型的な部分は完全です。 基本的な概念とアイデンティティが与えられています。 ポイントベースは、さまざまなアプリケーションに役立つ強力なツールです。 最後の記事では、最も単純な構造の基礎、つまり星の形を検討します。