はじめに
Pythonツールを使用した線形プログラミングでは、私の記事[1]で、メインの目標関数に代わる目標関数を使用した最適化問題の解決策を検討しました。 この記事で示したように、1つの一般的な最適化問題を検討するときに新しいターゲット関数を導入する手法は、メソッドの分析機能を大幅に拡張します。 したがって、一般的な最適化問題を解決するときに、いくつかの代替ターゲット関数を定式化できる例を選択して検討することは論理的です。
問題の声明
最適な食事問題の例を使用して、必要な初期条件でさまざまな代替ターゲット機能の形成を検討します。 さらに、エンドユーザーが理解できる結果を導き出し、そのような問題を解決するためのシンプルで統一されたインターフェイスを開発します。
食事のコストを最小化する目的関数と初期条件の形成
通常の生活を維持するためには、1日あたり少なくとも118 gのタンパク質、56 gの脂肪、500 gの炭水化物、28 gのミネラル塩を消費する必要があります。 これらの栄養素は、さまざまな量でさまざまな食品に含まれています。
この表には、さまざまな製品の栄養素の量(g / kg)およびこれらの製品の1 kgあたりの条件付き価格が示されています。 栄養素の最小摂取量を最小コストで含む毎日の食事を作成する必要があります 。
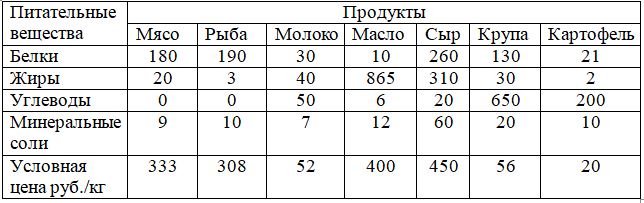
指定方法:X1-肉の数。 X2は魚の数です。 X3は牛乳の量です。 X4はオイルの量です。 X5-チーズの量。 X6-穀物の数; X7は、1人が1日に消費するジャガイモの量です。 1日あたりの総食品費Fの方程式を作成できます。
F = 333 * X1 + 308 * X2 + 52 * X3 + 400 * X4 + 450 * X5 + 56 * X6 + 25 * X7
最小のFを見つける必要があります。
人間の食事中のタンパク質の総量は、少なくとも118 gでなければなりません。
180 * X1 + 190 * X2 + 30 * X3 + 10 * X4 + 260 * X5 + 130 * X6 + 21 *X7≥118
脂肪、炭水化物、塩についても同じ不平等を作ります。 私たちが持っています:
20 * X1 + 3 * X2 + 40 * X3 + 865 * X4 + 310 * X5 + 30 * X6 + 2 *X7≥56
50 * X3 + 6 * X4 + 20 * X5 + 650 * X6 + 200 *X7≥500
9 * X1 + 10 * X2 + 7 * X3 + 12 * X4 + 60 * X5 + 20 * X6 + 10 *X7≥28
問題を解決しましょう
from cvxopt.modeling import variable, op import time start = time.time() x = variable(7, 'x') z=(333*x[0] + 308*x[1] +52* x[2] +400*x[3] +450*x[4] +56* x[5]+20*x[6]) mass1 =(- (180*x[0] + 190*x[1] +30* x[2] +10*x[3] +260*x[4] +130* x[5]+21*x[6]) <= -118) mass2 =(- (20*x[0] + 3*x[1] +40* x[2] +865*x[3] +310*x[4] +30* x[5]+2*x[6]) <= -56) mass3 =(- (50* x[2] +6*x[3] +20*x[4] +650* x[5]+200*x[6]) <= -500) mass4 =(- (9*x[0] + 10*x[1] +7* x[2] +12*x[3] +60*x[4] +20* x[5]+10*x[6]) <= -28) x_non_negative = (x >= 0) problem =op(z,[mass1,mass2,mass3,mass4 ,x_non_negative]) problem.solve(solver='glpk') problem.status print(":") print(round(1000*x.value[0],1),'- , -',round(x.value[0]*333,1),'.') print(round(1000*x.value[1],1),'- , -',round(x.value[1]*308,1),'.') print(round(1000*x.value[2],1),'- , -',round(x.value[2]*52,1),'.') print(round(1000*x.value[3],1),'- , -',round(x.value[3]*400,1),'.') print(round(1000*x.value[4],1),'- , -',round(x.value[4]*450,1),'.') print(round(1000*x.value[5],1),'- , -',round(x.value[5]*56,1),'.') print(round(1000*x.value[6],1),'- , -',round(x.value[6]*25,1),'.') print(round(problem.objective.value()[0],1),"- ") stop = time.time() print (" :",round(stop-start,3))
cvxoptモジュールを使用してプログラムを作成するいくつかの機能に注意する必要があります。 モデリング:すべての変数はリストに格納され、リストのインデックスは1ではなく0で始まります。 非厳密な不等式の形式で記述された条件下では、 上限を設定する必要があります 。したがって、下限から進むには、不等式の両側に-1を掛けます。
結果:
肉0.0グラム、コスト-0.0ルーブル。
魚の0.0グラム、コスト-0.0ルーブル。
牛乳0.0ミリリットル、コスト-0.0ルーブル。
オイル38.0グラム、コスト-15.2ルーブル。
-0.0グラムのチーズ、費用-0.0ルーブル。
穀物679.3グラム、コスト38.0ルーブル。
ジャガイモ1395.9グラム、コスト-34.9ルーブル。
81.1-1日1人の食事の費用
時間:0.09
カロリー食事を最小限にするための目的関数と初期条件の形成
明確にするために、最初の製品としてパン、肉、チーズ、バナナ、きゅうり、トマト、ブドウを考えてみましょう。たった7つの製品です。 栄養素として-タンパク質、脂肪、炭水化物。
各製品の1重量単位のカロリー含有量は次のとおりです。c1= 2060、c2 = 2430、c3 = 3600、c4 = 890、c5 = 140、c6 = 230、c7 = 650。
食品中の栄養素の含有量を次の表に示します。
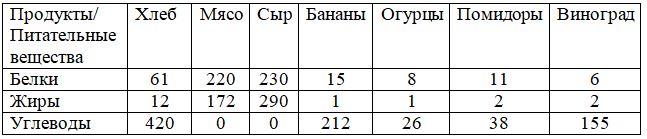
人間が毎日必要とする栄養素の最小量は次のとおりです。タンパク質ではb1 = 100、脂肪ではb2 = 70、炭水化物ではb3 = 400です。
解決される問題の一般性を低下させることなく、製品のカロリー含有量はキロカロリー/ kgで測定され、1日の栄養所要量はグラムで、製品の栄養含有量はグラム/ kgであると仮定できます。 これらの条件下では、目的関数の物理的次元と制約を考慮して、形成された問題の条件の追加検証を実行することが可能になります。
意味:x1 –パンの数。 x2は肉の量です。 x3はチーズの量です。 x4はバナナの数です。 x5はキュウリの数です。 x6はトマトの数です。 x7は、1人がキログラム単位で消費するブドウの数です。
1日あたりのF栄養の総カロリー量の方程式を作成できます。
F = 2060 * x1 + 2430 * x2 + 3600 * x3 + 890 * x4 + 140 * x5 + 230 * x6 + 650 * x7
最小のFを見つける必要があります。
人間の食事に含まれるタンパク質の総量は少なくとも100 gでなければなりません。
61 * x1 + 220 * x2 + 230 * x3 + 15 * x4 + 8 * x5 + 11 * x6 + 6 * x7≥100
脂肪と炭水化物についても同じ不平等を作ります。 私たちが持っています:
12 * x1 + 172 * x2 + 290 * x3 + 1 * x4 + 1 * x5 + 2 * x6 + 2 * x7≥70
420 * x1 + 0 * x2 + 0 * x3 + 212 * x4 + 26 * x5 + 38 * x6 + 155 * x7≥400
問題を解決しましょう
from cvxopt.modeling import variable, op import time start = time.time() x = variable(7, 'x') z=(333*x[0] + 308*x[1] +52* x[2] +400*x[3] +450*x[4] +56* x[5]+20*x[6]) mass1 =(- (180*x[0] + 190*x[1] +30* x[2] +10*x[3] +260*x[4] +130* x[5]+21*x[6]) <= -118) mass2 =(- (20*x[0] + 3*x[1] +40* x[2] +865*x[3] +310*x[4] +30* x[5]+2*x[6]) <= -56) mass3 =(- (50* x[2] +6*x[3] +20*x[4] +650* x[5]+200*x[6]) <= -500) mass4 =(- (9*x[0] + 10*x[1] +7* x[2] +12*x[3] +60*x[4] +20* x[5]+10*x[6]) <= -28) x_non_negative = (x >= 0) problem =op(z,[mass1,mass2,mass3,mass4 ,x_non_negative]) problem.solve(solver='glpk') problem.status print(":") print(round(1000*x.value[0],1),'- ') print(round(1000*x.value[1],1),'- ') print(round(1000*x.value[2],1),'- ') print(round(1000*x.value[3],1),'- ') print(round(1000*x.value[4],1),'- ') print(round(1000*x.value[5],1),'- ') print(round(1000*x.value[6],1),'- ') print(round(problem.objective.value()[0],1),"- ") stop = time.time() print (" :",round(stop-start,3))
結果:
0.0グラムのパン
211.5グラムの肉
チーズ109.4グラム
1886.8グラムのバナナ
きゅうり0.0グラム
トマト0.0グラム
0.0グラムのブドウ
1日あたり2587.1カロリー-カロリー摂取
時間:0.06
ユーザーの好みに応じた製品の選択中に、食事のカロリー量を最小化するための目的関数と初期条件の形成
たとえば、製品の条件付きセットを作成します。 製品のカロリー含有量の初期条件は、前の問題の解決策から取得されます。
問題解決
from cvxopt.modeling import variable, op import time start = time.time() x = variable(7, 'x') z=( x[0] + x[1] +x[2] +x[3] +x[4] +x[5]+x[6]) mass1 =(- (61*x[0] + 220*x[1] +230* x[2] +15*x[3] +8*x[4] +11* x[5]+6*x[6]) <= -100) mass2 =(- (12*x[0] +172*x[1] +290* x[2] +1*x[3] +1*x[4] +2* x[5]+2*x[6]) <= -70) mass3 =(- (420*x[0] +0*x[1] +0* x[2] +212*x[3] +26*x[4] +38* x[5]+155*x[6]) <= -400) mass4 =(-( 2060*x[0] + 2430*x[1] +3600* x[2] +890*x[3] +140*x[4] +230* x[5]+650*x[6]) <= -3000) x_non_negative = (x >= 0) problem =op(z,[mass1,mass2,mass3, mass4,x_non_negative]) problem.solve(solver='glpk') problem.status print(":") print(round(1000*x.value[0],1),'- ') print(round(1000*x.value[1],1),'- ') print(round(1000*x.value[2],1),'- ') print(round(1000*x.value[3],1),'- ') print(round(1000*x.value[4],1),'- ') print(round(1000*x.value[5],1),'- ') print(round(1000*x.value[6],1),'- ') print(round(problem.objective.value()[0],1),"-- \n ") stop = time.time() print (" :",round(stop-start,3))
結果:
952.4グラムのパン
0.0グラムの肉
チーズ288.4グラム
0.0グラムのバナナ
きゅうり0.0グラム
トマト0.0グラム
0.0グラムのブドウ
1.2キログラム-製品の総質量
1日1人の食事
時間:0.051
自明であるため、問題を解決した結果についてはコメントしません。 さらに、初期データは任意であり、最後のタスクではそれらは個別です。
実用的な結論またはこれがすべて必要な理由
プログラムインターフェイスは非常にシンプルで直感的であるため、追加のスキルは必要ありません。 たとえば、サイト[2]から最新バージョンのPythonをダウンロードし、サイト[3]からcvxoptライブラリをダウンロードしてインストールすれば十分です。 次に、拡張子がpyのファイルを作成し、記事にリストされているプログラムのいずれかに配置します。これには、新しいターゲット関数と制限を使用してタスク用に以前に変更しました。