物理学の実験室ワークショップを実施する過程で、私はしばしば、さらなる計算を実施するために、紙に提示されたグラフに従って関数の値を決定するタスクに直面します。 このようなグラフをコンピューターで処理すると、このプロセスの速度と精度が大幅に向上するため、グラフをデジタル化し、グラフに表示される曲線の数学モデルを構築する可能性を検討することにしました。
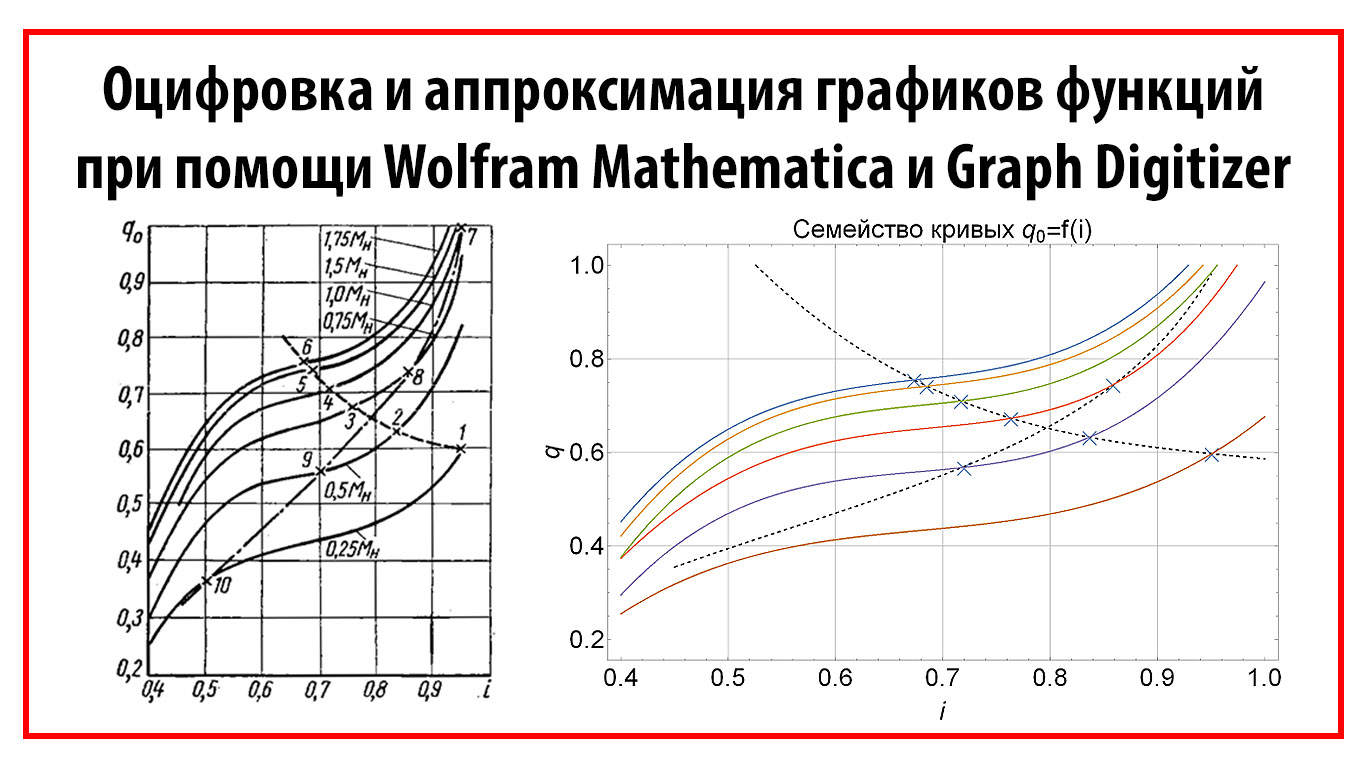
例として、電気工学に関する実験室のワークショップから、発電機の効率の電力依存性のグラフを取りました。 作業の入力時に、グラフをスキャンし、グラフの画像を処理し、座標をデジタル化し、曲線の数学モデルを構築しました。
1.画像の準備
スキャン後、最初のステップは、結果の画像をフルコントラストにし、グラフの軸の1つを揃えることです。 次に、画像をシャープにしてサイズを変更します。 サイズと解像度が大きすぎると、その後の作業段階で問題が発生します。
画像処理Adobe Photoshopプログラムをお勧めします。 カーブツールを使用して完全なコントラストを実現し、スマートシャープフィルターを使用してシャープネスを高めます。 Photoshopの間違いない利点は、アクション(アクション)を記録し、それをバッチ処理(ファイル-バッチ処理)と組み合わせて適用することにより、多数の画像を処理できることです。
プロセスを高速化するために、事前に準備されたプリセットまたは自動アルゴリズムを使用して、スキャンプログラムで処理を実行できます。

図1.1-処理前と処理後のグラフの画像
2.座標のデジタル化
座標をデジタル化するために、シェアウェアGetData Graph Digitizeバージョン2.26を使用しました。 プログラムを開始した後、処理済みのイメージ「ファイル-イメージを開く」を開きます。 開くと、標準のワークスペースが表示されます。
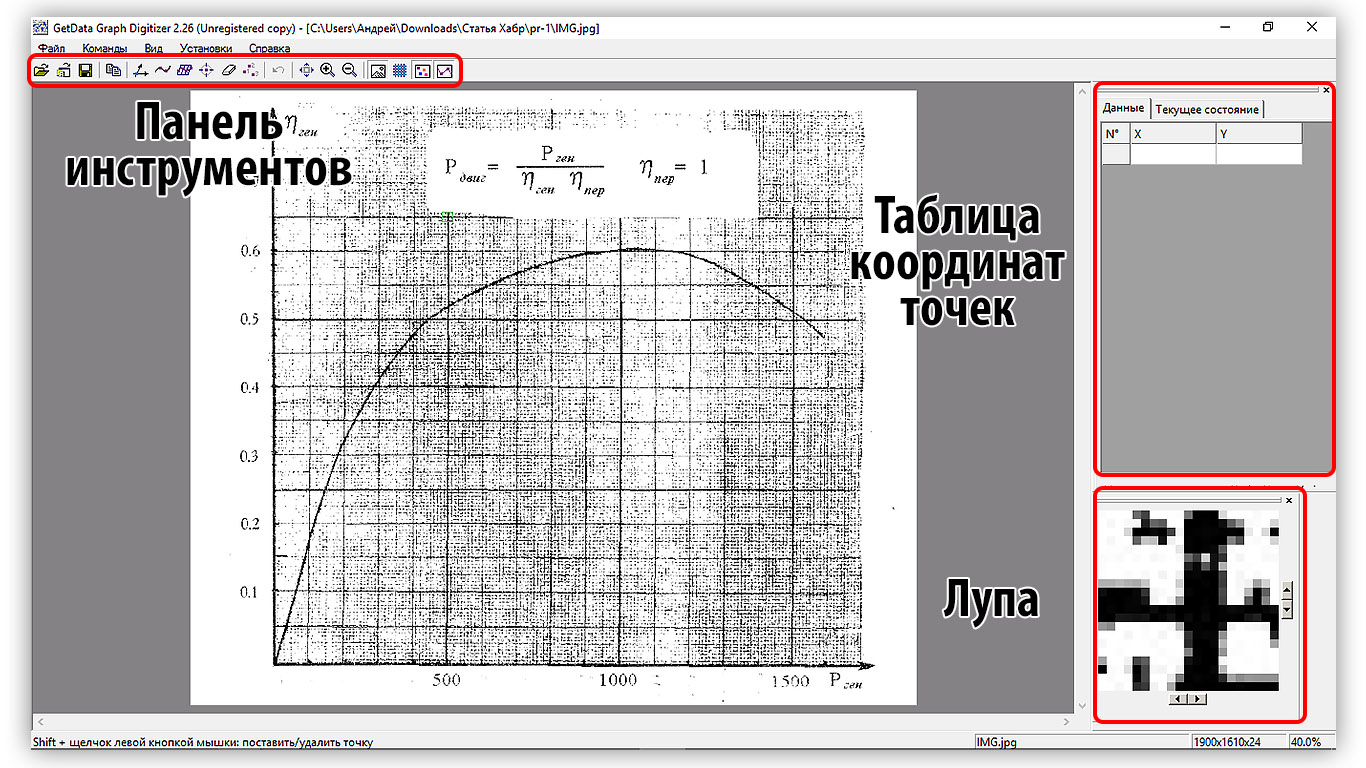
図2.1-標準グラフデジタイズインターフェイス
2.1。 座標系の設定(SK)
最初に行う必要があるのは、座標系を確立することです。 軸線をマークします。 これを行うには、「コマンド-座標系の設定」に進みます。 次に、LMBを押しながら、原点を見つけてクリックします。 表示されるウィンドウで、原点の値(Xmin)を入力します。 次に、Xmax、Ymin、Ymaxの値を同様に設定します。 ポイントの便利な設定のために、拡大鏡のウィンドウを開く必要があります "View-Magnifier"。 制御点を設定すると、軸線が表示され、[座標系パラメーター]ウィンドウが開きます。このウィンドウでは、制御点の値を再割り当てし、対数軸スケールを設定できます。
SKインストールの品質を視覚的に制御するために、指定されたステップ「表示-グリッドの表示」でグリッドを表示できます。 SCを正しくインストールする場合、グリッド線はグラフ画像の線と厳密に平行でなければなりません。 ターンをスキャンすると、グラフがベンド領域に表示されることが多く、軸の1つが湾曲していることに注意してください。 この場合、SCを正しく確立することはできません。そのため、スキャン段階では、ターンをガラスにより強く押し付ける必要があります。

図2.2-座標系とグリッドがインストールされたビュー
2.3。 数値化曲線
チャートにポイントを設定しましょう。 これを行うには、ポイント設定モードに移動します(Ctrl + P)。 このモードでは、LMBをクリックして新しいポイントを設定します。 選択したポイントの座標テーブルを表示するには、「表示-情報ウィンドウ」に進みます。 ポイントを削除するには、データポイントの消しゴム「コマンド-データポイントの消しゴム」を使用します(Ctrl + E)
私の経験では、曲線の変曲点の近くに多数のポイントを設定する必要があります;曲線の線形セクションでは、それらを少数に制限できます。
グラフ上に複数の曲線または曲線のファミリがある場合、最初のポイントを設定した後、「コマンド-行の追加」という新しい行を追加する必要があります。 その後、2番目の曲線などに点を設定することができます。
グラフ画像にグリッドがない場合は、自動曲線追跡アルゴリズム(Ctrl + T)を使用できます。 グリッドがある場合、アルゴリズムは多くのエラーを生成します。
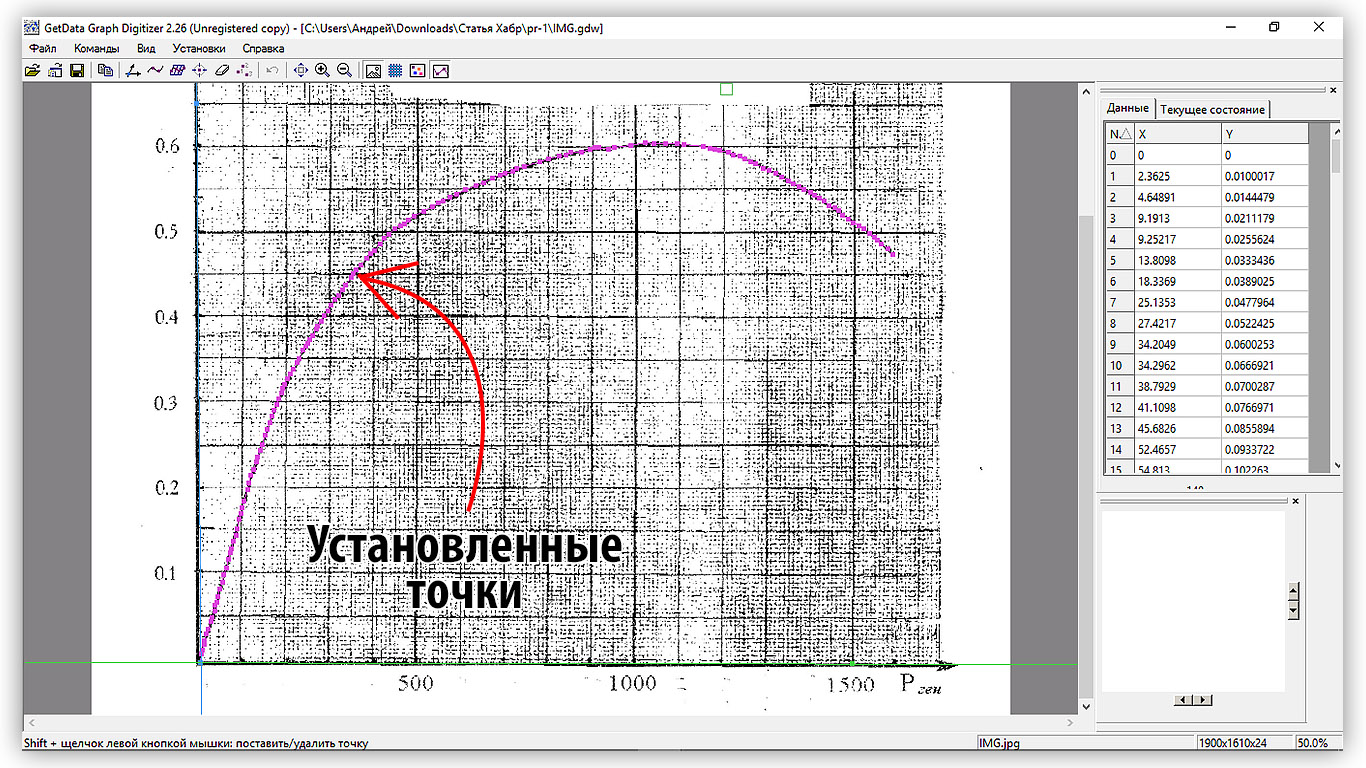
図2.3-曲線上に固定点があるビュー
2.4。 データエクスポート
取得したデータをさらに処理するには、ポイントの座標を.txtファイルまたはクリップボードにエクスポートする必要があります(カーブが1つしかない場合に便利です)。 GetData Graph Digitizeプログラムでは、「File-Data Export」コマンド(Ctrl + Alt + E)を呼び出して.txtへのエクスポートを実行します。 開いたウィンドウをクリックした後、保存パスとファイル名を設定することをお勧めします。
データファイルのエクスポート
作成者GetData Graph Digitizer 2.26.0.20、作成日2017年10月1日、21:16、
ファイル「C:\ Users \ Andrey \ Downloads \ Article Habr \ pr-1 \ IMG.jpg」に基づいて
行番号1
0.00000000000000 0.00000000000000
2.36249828804472 0.0100017499987319
4.64890967470313 0.0144478880812405
9.19129768746544 0.0211179194797685
9.25216720857449 0.0255624090127471
13.8097726016141 0.0333435627945197
18.3369432340991 0.0389024718098030
25.1353078729653 0.0477963965243503
27.4217192596237 0.0522425346068590
34.2048665182127 0.0600253369381616
34.2961707998762 0.0666920712376295
38.7929066718068 0.0700287354864236
41.1097528190197 0.0766971183354215
45.6825755923365 0.0855893945004388
52.4657228509255 0.0933721968317414
54.8130037586929 0.102262824447229
61.5961510172819 0.110045626778531
66.1841911708760 0.120049025326793
70.7417965639155 0.127830179108566
73.0282079505739 0.132276317191075
77.6010307238908 0.141168593356092
84.3689606022025 0.147840273304150
86.7010241296927 0.155619778536392
91.3042816635640 0.166734299467899
95.8466696763263 0.173404330866427
98.1635158235393 0.180072713715425
102.721121216579 0.187853867497197
111.805897242103 0.201193930294253
114.137960769594 0.208973435526496
118.710783542910 0.217865711691513
125.478713421222 0.224537391639571
132.277078060088 0.233431316354119
134.578706827024 0.238988576819872
141.361854085613 0.246771379151175
145.904242098375 0.253441410549703
152.733041497796 0.264557580030739
157.275429510558 0.271227611429267
164.058576769147 0.279010413760570
168.616182162187 0.286791567542342
173.158570174949 0.293461598940870
179.926500053261 0.300133278888928
184.468888066023 0.306803310287456
191.236817944335 0.313474990235514
193.538446711271 0.319032250701268
198.050399963478 0.323480037333306
204.818329841790 0.330151717281364
211.571042339824 0.335712274846178
218.323754837859 0.341272832410991
227.332443961997 0.349057283291824
231.844397214205 0.353505069923862
240.883521098898 0.363511765571184
247.621016216655 0.367961200752753
252.117752088585 0.371297865001547
256.629705340793 0.375745651633586
263.367200458550 0.380195086815154
272.375889582689 0.387979537695987
274.647083589070 0.391314553395251
283.625337952654 0.396876759509595
290.393267830965 0.403548439457653
299.371522194549 0.409110645571996
306.139452072861 0.415782325520054
315.132923816722 0.422455654017642
324.095960800028 0.426906737748741
333.089432543889 0.433580066246329
339.842145041924 0.439140623811142
353.317135277438 0.448039494174280
357.829088529646 0.452487280806318
364.566583647403 0.456936715987887
375.770379876536 0.462500570651760
389.230152731773 0.470288318631653
398.208407095357 0.475850524745997
407.156226698386 0.479190486093851
420.615999553624 0.486978234073743
429.609471297485 0.493651562571331
440.798050146340 0.498104294851960
454.242605621300 0.504780920448608
467.641508955428 0.508124178895523
476.574111178180 0.510353017860132
485.537148161487 0.514804101591231
498.951268875892 0.519258482421390
521.282774432772 0.524830579832913
541.388738124103 0.530401028694907
554.802858838508 0.534855409525066
565.961002926809 0.537085897039205
581.600665506764 0.541541926418894
597.225110706442 0.544886833415338
617.331074397772 0.550457282277332
641.872904439924 0.554919905855141
659.722891505151 0.558266461401115
679.828855196482 0.563836910263109
697.678842261709 0.567183465809083
708.836986350010 0.569413953323222
726.671756034959 0.571649386485952
735.619575637989 0.574989347833806
753.454345322938 0.577224780996536
789.139102073114 0.582806769705239
809.214631003891 0.586154973800744
833.741243665765 0.589506474995308
849.335254104888 0.590629137225263
860.508615573467 0.593970747122647
884.989576094510 0.593988881167477
905.065105025286 0.597337085262982
916.223249113588 0.599567572777121
925.125416575785 0.599574166975241
947.350400470724 0.597368407704052
960.734086424575 0.599600543767722
998.598732899469 0.601850813876222
1032.02751302354 0.605208909268906
1052.04217243321 0.604112623831432
1078.74867481980 0.604132406425792
1105.45517720639 0.604152189020153
1121.01875288496 0.603052606483618
1165.49915543539 0.600863332707730
1181.04751373369 0.598652627787951
1192.16000568116 0.597549748152356
1203.27249762862 0.596446868516762
1223.27193965801 0.594239460696043
1234.35399684493 0.590914336293959
1249.91757252350 0.589814753757425
1260.99962971041 0.586489629355341
1274.30722876288 0.583166153502787
1285.40450333007 0.580952151483948
1303.13275135308 0.575409727963965
1316.45556778582 0.573197374494656
1331.98870870383 0.569875547191632
1345.28109037602 0.565440948955834
1360.79901391376 0.561007999269566
1371.88107110067 0.557682874867482
1385.18867015314 0.55435939901494928
1396.27072734005 0.551034274612844
1411.80386825807 0.547712447309821
1420.66038357943 0.544385674358207
1431.74244076635 0.541060549956123
1442.82449795326 0.537735425554039
1453.87612037962 0.532188056385466
1467.19893681236 0.529975702916157
1476.05545213373 0.526648929964543
1484.88153269454 0.521099912246440
1498.17391436673 0.516665314010642
1509.24075417337 0.512229067225314
1522.54835322583 0.508905591372760
1533.63041041275 0.505580466970676
1546.90757470466 0.500034746351633
1557.97441451129 0.495598499566305
1564.60538796711 0.492270078065161
1573.44668590820 0.487832182730302
1588.94939206566 0.482288110660789
1599.98579711174 0.475629619108972
ファイル「C:\ Users \ Andrey \ Downloads \ Article Habr \ pr-1 \ IMG.jpg」に基づいて
行番号1
0.00000000000000 0.00000000000000
2.36249828804472 0.0100017499987319
4.64890967470313 0.0144478880812405
9.19129768746544 0.0211179194797685
9.25216720857449 0.0255624090127471
13.8097726016141 0.0333435627945197
18.3369432340991 0.0389024718098030
25.1353078729653 0.0477963965243503
27.4217192596237 0.0522425346068590
34.2048665182127 0.0600253369381616
34.2961707998762 0.0666920712376295
38.7929066718068 0.0700287354864236
41.1097528190197 0.0766971183354215
45.6825755923365 0.0855893945004388
52.4657228509255 0.0933721968317414
54.8130037586929 0.102262824447229
61.5961510172819 0.110045626778531
66.1841911708760 0.120049025326793
70.7417965639155 0.127830179108566
73.0282079505739 0.132276317191075
77.6010307238908 0.141168593356092
84.3689606022025 0.147840273304150
86.7010241296927 0.155619778536392
91.3042816635640 0.166734299467899
95.8466696763263 0.173404330866427
98.1635158235393 0.180072713715425
102.721121216579 0.187853867497197
111.805897242103 0.201193930294253
114.137960769594 0.208973435526496
118.710783542910 0.217865711691513
125.478713421222 0.224537391639571
132.277078060088 0.233431316354119
134.578706827024 0.238988576819872
141.361854085613 0.246771379151175
145.904242098375 0.253441410549703
152.733041497796 0.264557580030739
157.275429510558 0.271227611429267
164.058576769147 0.279010413760570
168.616182162187 0.286791567542342
173.158570174949 0.293461598940870
179.926500053261 0.300133278888928
184.468888066023 0.306803310287456
191.236817944335 0.313474990235514
193.538446711271 0.319032250701268
198.050399963478 0.323480037333306
204.818329841790 0.330151717281364
211.571042339824 0.335712274846178
218.323754837859 0.341272832410991
227.332443961997 0.349057283291824
231.844397214205 0.353505069923862
240.883521098898 0.363511765571184
247.621016216655 0.367961200752753
252.117752088585 0.371297865001547
256.629705340793 0.375745651633586
263.367200458550 0.380195086815154
272.375889582689 0.387979537695987
274.647083589070 0.391314553395251
283.625337952654 0.396876759509595
290.393267830965 0.403548439457653
299.371522194549 0.409110645571996
306.139452072861 0.415782325520054
315.132923816722 0.422455654017642
324.095960800028 0.426906737748741
333.089432543889 0.433580066246329
339.842145041924 0.439140623811142
353.317135277438 0.448039494174280
357.829088529646 0.452487280806318
364.566583647403 0.456936715987887
375.770379876536 0.462500570651760
389.230152731773 0.470288318631653
398.208407095357 0.475850524745997
407.156226698386 0.479190486093851
420.615999553624 0.486978234073743
429.609471297485 0.493651562571331
440.798050146340 0.498104294851960
454.242605621300 0.504780920448608
467.641508955428 0.508124178895523
476.574111178180 0.510353017860132
485.537148161487 0.514804101591231
498.951268875892 0.519258482421390
521.282774432772 0.524830579832913
541.388738124103 0.530401028694907
554.802858838508 0.534855409525066
565.961002926809 0.537085897039205
581.600665506764 0.541541926418894
597.225110706442 0.544886833415338
617.331074397772 0.550457282277332
641.872904439924 0.554919905855141
659.722891505151 0.558266461401115
679.828855196482 0.563836910263109
697.678842261709 0.567183465809083
708.836986350010 0.569413953323222
726.671756034959 0.571649386485952
735.619575637989 0.574989347833806
753.454345322938 0.577224780996536
789.139102073114 0.582806769705239
809.214631003891 0.586154973800744
833.741243665765 0.589506474995308
849.335254104888 0.590629137225263
860.508615573467 0.593970747122647
884.989576094510 0.593988881167477
905.065105025286 0.597337085262982
916.223249113588 0.599567572777121
925.125416575785 0.599574166975241
947.350400470724 0.597368407704052
960.734086424575 0.599600543767722
998.598732899469 0.601850813876222
1032.02751302354 0.605208909268906
1052.04217243321 0.604112623831432
1078.74867481980 0.604132406425792
1105.45517720639 0.604152189020153
1121.01875288496 0.603052606483618
1165.49915543539 0.600863332707730
1181.04751373369 0.598652627787951
1192.16000568116 0.597549748152356
1203.27249762862 0.596446868516762
1223.27193965801 0.594239460696043
1234.35399684493 0.590914336293959
1249.91757252350 0.589814753757425
1260.99962971041 0.586489629355341
1274.30722876288 0.583166153502787
1285.40450333007 0.580952151483948
1303.13275135308 0.575409727963965
1316.45556778582 0.573197374494656
1331.98870870383 0.569875547191632
1345.28109037602 0.565440948955834
1360.79901391376 0.561007999269566
1371.88107110067 0.557682874867482
1385.18867015314 0.55435939901494928
1396.27072734005 0.551034274612844
1411.80386825807 0.547712447309821
1420.66038357943 0.544385674358207
1431.74244076635 0.541060549956123
1442.82449795326 0.537735425554039
1453.87612037962 0.532188056385466
1467.19893681236 0.529975702916157
1476.05545213373 0.526648929964543
1484.88153269454 0.521099912246440
1498.17391436673 0.516665314010642
1509.24075417337 0.512229067225314
1522.54835322583 0.508905591372760
1533.63041041275 0.505580466970676
1546.90757470466 0.500034746351633
1557.97441451129 0.495598499566305
1564.60538796711 0.492270078065161
1573.44668590820 0.487832182730302
1588.94939206566 0.482288110660789
1599.98579711174 0.475629619108972
「設定-パラメータ」メニューで、データ出力の形式が設定されます。 ここで、X座標の値でポイントを並べ替えることができます。各Xの曲線に一意のYがある場合、一連の設定ポイントのランダムエラーを除外します。

図2.4-エクスポート設定
3.曲線の数学モデルの構築
最後に、取得したデータの近似を実行し、取得した数学モデルの正確性を確認します。 このために、Wolfram Mathematicaコンピューター代数システムを使用することをお勧めします。
Wolfram Mathematicaにデータをすばやくインポートするには、エクスポートされたファイルからポイントの座標をコピーして空のExcelセルに貼り付けます。 その結果、データXとYの2列がそれぞれシートに表示されます。
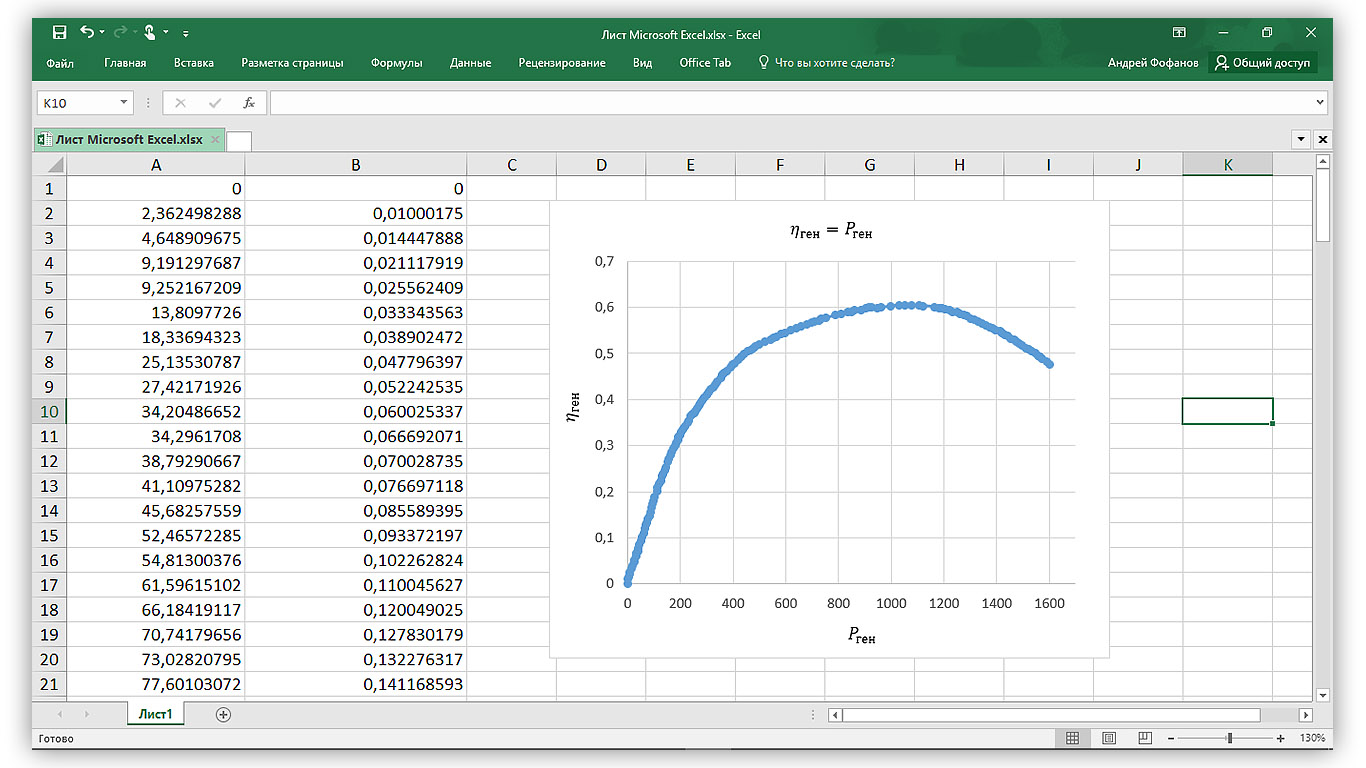
図3.1-Excelのデータ
次のステップは、新しいWolfram Mathematicaドキュメントを作成し、Excelファイルをそこにドラッグすることです。 その結果、ポイントの座標を含むリストのリストが形成されます。 変数データをそれに割り当てます。

図3.2-Wolfram Mathematicaにインポートされたデータ
ListPlot []関数を使用して、インポートされたデータを表示します。

図3.3-データ散布図形式のポイントのグラフィカル表示
5次の多項式でポイントを近似します。 これを行うには、LinearModelFit []関数を使用します。 その結果、クラスFittedModel []のオブジェクトを取得します。 フィットするように設定します。
決定係数R ^ 2を計算し、変数の変動(広がり)が方程式をどの程度説明するかを示します。 この係数が1に近いほど、方程式が説明する変動の割合が大きくなります。 これを行うには、「RSquared」をfit関数の引数として指定します。 この場合、R ^ 2 = 0.99です。これは、モデルが変数の変動の99.9%を説明することを意味します。
Yの値を計算するには、必要なXの値をfit関数の引数として指定する必要があります。

図3.4-ポイントの近似、決定係数の計算、および関数の値の計算
決定係数の計算に加えて、回帰分析を実施します。 今回は、フィット関数の引数として「ANOVATable」を指定します。 結果によると、近似多項式の各項の使用は正当化されると主張できます。 得られた方程式を明示的な形式で表示します;このために、フィット変数にNormal []関数を適用します。

図3.5-回帰分析と明示的な形式の多項式
次に、多項式をプロットし、その開始点を表示します。 標準の構文を使用して、チャートスタイルを構成し、軸にラベルを追加し、チャート名を追加します。

図3.6-最終的なグラフ
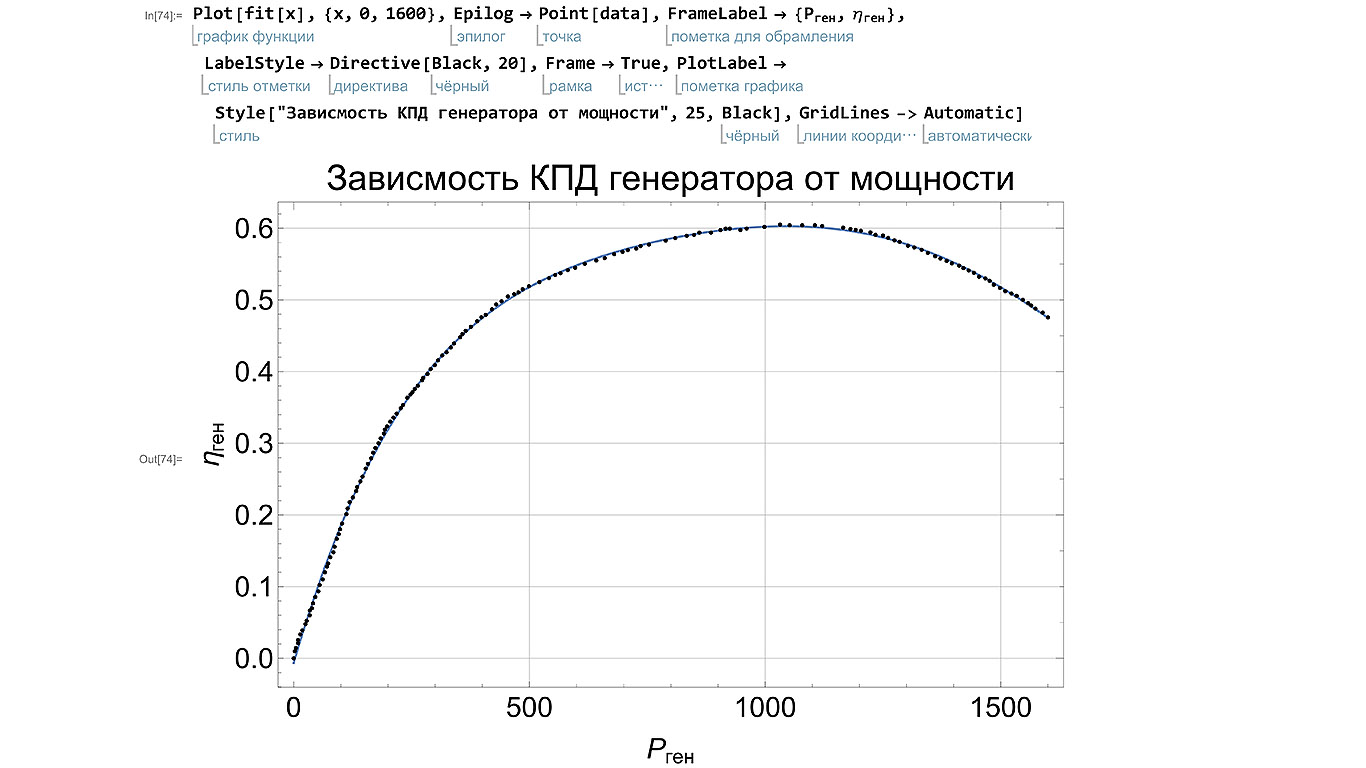
図3.7-最終グラフとソースデータの比較
Wolfram Mathematicaで数学モデルを分析する可能性は本当に大きいが、我々は上記のものに限定するつもりである。 興味のある方は、fit ["Properties"]関数を評価することでさらに学ぶことができます。
結論:
その結果、グラフをデジタル化し、曲線の数学モデルを選択するためにWolfram MathematicaとGraph Digitizerを使用する可能性を調査しました。 使用済みソフトウェアを使用すると、最小限の労力で高品質のタスクを完了できます。
PS:簡単に説明すると、仕事で同じような仕事にどれくらいの頻度で直面する必要があるか教えていただけますか? 私は質問に答えてうれしいです。