パート1.マルコフ連鎖を使用して勝つための最小移動数の計算

最近の更新の後、 2048ゲームの「You win！」画面に勝つために必要な動きの数が表示されるようになりました。



記事の最初の部分では、ゲーム2048をマルコフチェーンの形でシミュレートし、分析して、プレイヤーのスキルに関係なく、 平均で少なくとも938.8の動きが勝つために必要であることを示すことで、この質問に答えます。 これは私たちに良いベンチマークを提供します-あなたがそのような数の動きについて勝つことができるなら、あなたはうまくプレーします。



ゲームはタイル2



と4



ランダムに追加するため、勝つために必要な動きの数はランダム性に依存します。 また、分析により、勝つ前の最小移動数の分布の標準偏差は8.3移動であり、その全体的な形状は二項分布の混合によって近似されていることがわかります。



これらの結果を得るために、2048の簡易バージョンを使用します。フィールドにタイルを配置する代わりに、...バッグに入れます。 つまり、タイルを組み合わせることができるフィールドの形状によって課される幾何学的制限を無視します。 この単純化により、プレーヤーが決定を行う必要がなくなり¹ 、フィールド上のタイルの位置を追跡する必要がないため、作業が非常に容易になります。



これらの幾何学的制約を取り除くことの代価は、勝利する前に予想される動きの下限のみを計算できることです。 幾何学的制約によりこの境界に到達できない場合があります。 ただし、2048年に多くのゲームをプレイしたため（科学のため！）、実際にはこの境界に近づくことができることも示します。



2048やマルコフチェーンに慣れていない場合は、心配しないでください。必要な概念については記事全体で説明します。 コードを研究してチェーンとグラフを生成する場合に備えて、記事の執筆に基づいた（研究品質の）コードにはオープンソースがあります 。

2048マルコフ連鎖として

単純化したゲーム「2048 in a bag」をマルコフ連鎖として提示するには、連鎖の状態と遷移確率を指定する必要があります。 各状態は、特定の時点でのゲームの「キャスト」のようなものであり、遷移確率は各状態の遷移確率を設定します。



ここでは、現在各バッグにあるタイルを各状態でエンコードします。 タイルの順序は気にしないので、タイルを多くのタイルとして認識できます。 最初は、バッグにはタイルがありません。つまり、初期状態は単なる空のセットです。 以下に追加する回路の形式では、この初期状態は次のようになります。

現地準備

新しいゲームの1ダースのフィールドの例。



2048年に新しいゲームを開始すると、ゲームは2つのランダムなタイルをフィールドに配置します（上記の例を参照）。 これをマルコフ連鎖で表すには、初期状態から可能な各状態への遷移確率を指定する必要があります。



幸いなことに、 ゲームのソースコードを調べて、ゲームの仕組みを理解できます。 ゲームがフィールドにランダムタイルを配置すると、常にこのシナリオに従います。 セルをランダムに選択し、値2



（0.9の確率）または値4



（0.1の確率）で新しいタイルを追加します 。



「2048 in a bag」の場合、無料のセルの検索について心配しません。バッグの容量に制限を設けていないからです。 与えられた確率でタイル2



または4



を追加することにのみ興味があります。 これにより、初期状態から次の3つの状態になります。

• $$$\左\ {2,2 \右\}$ 両方の新しいタイルの値が2
  
  
  
  。 確率で起こる $$ 。
• $$$\左\ {4,4 \右\}$ 両方の新しいタイルの値が4
  
  
  
  。 確率で起こる $$$0.1 \倍0.1 = $ 0.0$ 、つまり、2つの4でゲームを開始する場合、あなたはかなり幸運です。
• $$$\左\ {2,4 \右\}$ 新しいタイルの値が2
  
  
  
  で4
  
  
  
  場合、確率で発生します $$$0.9 \倍0.1 = $ 0.0$ 、または最初の4
  
  
  
  、次に2
  
  
  
  確率で発生します $$$0.1 \回0.9 = $ 0.0$ 。 私たちは順序を気にしないので、両方のケースが共通の確率で同じ状態になります $$ 。

これらの後続の状態と遷移確率を次のようにマルコフ回路図に追加できます（遷移確率はエッジに書き込まれ、新しいノードとエッジは青色でマークされます）。

ゲームをプレイする

タイルの最初のペアを配置したら、ゲームを開始する準備ができました。 実際のゲームでは、これはプレイヤーが同じタイルのペアを接続するために左、右、上または下にスワイプする必要があることを意味します。 ただし、バッグを使用したゲームでは、同じタイルのすべてのペアを結合することを妨げるものはありません。



バッグとゲーム内のタイルを結合するためのルールは次のとおりです。同じ値を持つタイルのすべてのペアをバッグ内で見つけ、それらを削除します。 次に、タイルの各ペアを値が ² 倍の1つのタイルに置き換えます 。



同一のタイルのペアを組み合わせて次の状態に移行した後、ゲームは上記のプロセスを使用して1つの新しいタイル、つまり確率が0.9のタイル2



または確率が0.1のタイル4



をランダムに追加します。



たとえば、可能な後続の状態状態を見つけるには $$$\左\ {2,2 \右\}$ 、最初に2つのタイル2



を1つのタイル4



に結合してから、ゲームがタイル2



またはタイル4



追加します。 したがって、可能な後続の状態は $$$\左\ {2,4 \右\}$ そして $$$\左\ {4,4 \右\}$ それが起こったとき、私たちは以前に会った。 次に、これらの2つの遷移を含む回路 $$$\左\ {2,2 \右\}$ 、それぞれ確率が0.9と0.1の形式は次のとおりです。











後続の状態状態に対してこのプロセスを実行し続ける場合 $$$\左\ {2,4 \右\}$ 、次に、同じタイルのペアがないため、ユニオンは不可能ですが、次の状態は $$$\左\ {2,2,4 \右\}$ または $$$\左\ {2,4,4 \右\}$ 、新しいタイルの値が2



か4



かによって異なります。 更新されたスキームは次のようになります。

レイヤーとスキップ

この方法で引き続きトランジションを追加できます。 ただし、新しい状態と遷移が追加されると、スキームはより複雑になる可能性があります³ 。 次の観察を使用して、スキームを少し合理化することができます。 バッグ内のタイルの合計は、遷移ごとに2または4増加します 。 これは、同じタイルのペアを組み合わせても、バッグ内（またはフィールド上-このプロパティは実際のゲームに適用される）のタイルの値の合計が変更されないためです。つまり、ゲームはタイル2



またはタイル4



追加します。



状態の合計を「レイヤー」にグループ化すると、最初のいくつかのレイヤーは次のようになります。









スキームのノイズレベルを下げるために、後のレイヤーでは、遷移のマークを0.9（実線、何らかの方法でマークされていない場合）および0.1（破線）の確率で示しません。



状態を合計によって層にグループ化すると、別の規則性が明らかになります：各遷移（初期状態からの遷移を除く）は、次の層で確率0.9で、またはその後の層で確率0.1で発生します。 （これは、上の図の8、10、および12のレイヤーを見ると特に明らかです。）つまり、ほとんどの場合、ゲームは2



を提供し、次のレイヤーに進みますが、幸運な場合があり、ゲームは4



を提供します。は、レイヤーをスキップできることを意味します。これにより、目標に少し近づき、タイル2048に到達します。

ゲームの終わり

このプロセスは永遠に続けることができますが、 2048



タイルに到達することのみに関心があるため、この時点で停止し、 2048



タイルの状態をすべて吸収します。 吸収状態には単一の遷移があり、確率1でそれ自体につながります。つまり、吸収状態に到達すると、それから抜け出すことはできなくなります。



この場合、すべての吸収状態は「勝利状態」です-タイル2048



を得たので、ゲームに勝ちました。 「かばんを使ったゲーム」では、「失う」方法はありません。なぜなら、実際のゲームとは異なり、フィールド（またはかばん）がいっぱいになると状況に陥ることができないからです。



2048



タイルを含む最初の状態は、2066の量のレイヤー内にあります。フィールド上で単一の2048



タイルを取得することは不可能です。タイル1024



、タイル512



などを結合するには、いくつかの動きが必要です。 したがって、 2048



タイルを持つ最初の状態のタイルの合計は2048



よりも大きくなります。



この最初の勝利状態の近くのグラフは次のとおりです（ 詳細を参照 ）。 吸収状態は赤で強調表示されます：











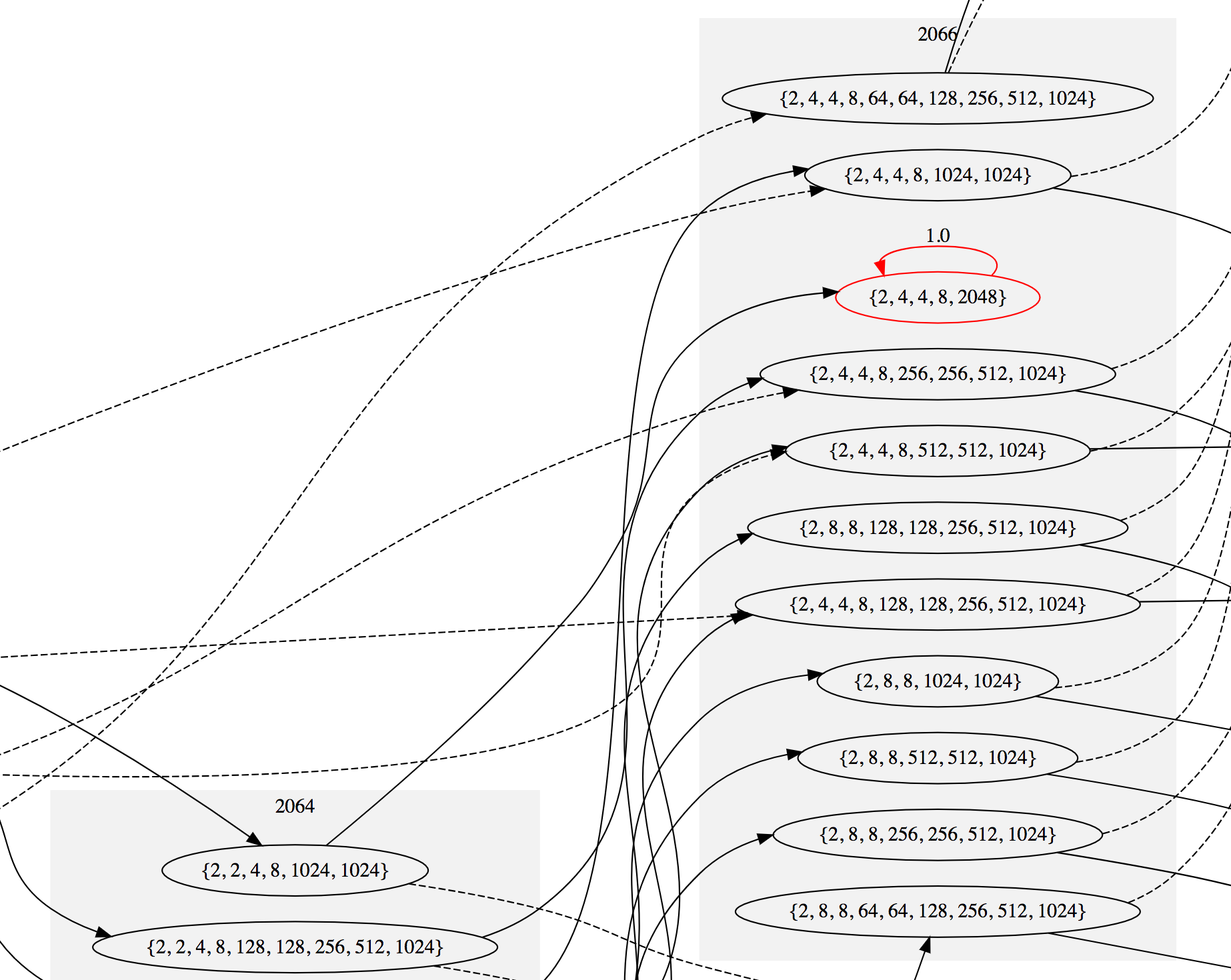
非吸収状態がなくなるまで遷移を追加し続けると、結果として3487状態が得られ、そのうち26状態が吸収されます。 これでマルコフ連鎖の定義は終わりです。 全回路図は非常に大きくなりますが、お使いのコンピューターが5メガバイトのSVGファイルを処理できる場合、全回路図がここにあります（最初を見るには少しスクロールする必要があるかもしれません）。 ズームアウトすると、次のようになります。

チェーンの選択

マルコフ連鎖の形で2048ゲーム（バッグ）のモデリングに多大な労力を費やしたので、すべての吸収状態に到達するために必要な動きの数を調べる必要があります。 これを行う最も簡単な方法は、シミュレーションを実行することです。 各シミュレーションでは、初期状態から始まり、遷移確率に比例してランダムに次の状態を選択し、この状態からプロセスを繰り返すチェーンに沿って1つのパスを生成します。 勝つための動きの数について100万のシミュレーションを完了すると、次の分布が明らかになります。











青色の縦線でマークされた平均は938.8移動に等しく、初期状態からの最初の遷移を除き、 8.3移動の標準偏差があります。 それで、ゲームに勝つ前の最小予想移動数についての質問に対する私たちの答えです！



マルコフ連鎖理論により、トリッキーな数学を使用してこれらの特性のいくつかを直接計算することもできます。 付録Aでは 、シミュレーションを使用せずに移動数の平均と標準偏差を計算する方法を示します。 次に、 付録Bでは 、回路のいくつかのプロパティを使用して、分布曲線の形状の少なくとも部分的な説明を提供します。

理論を実践でテストする

最後に、これらの結果を実際の生活でテストするために、私は2048年に何度もプレイしました（科学のためです！）そして、勝った28ゲームで、移動数と2048 ⁴タイルに達したときのフィールド上のタイルの合計を記録しました：











これらの数値をスプレッドシートに書き込んでプロットすると、次の散布図が得られました。











予想される最小移動数にプラスマイナス1標準偏差を青でマークし、赤で2066タイルの合計をマークしました。これは、2048タイルで可能な最小タイルの合計です。



フィールド上のタイルの合計は重要です。これは、タイルが大きい場合、通常、ミスを犯して別のタイルと組み合わせることができない場所から大きなタイルを運転したことを意味するためです。 次に、別の大きなタイルと組み合わせることができる場所でこのタイルを再構築（またはフィールドの構成を変更して適切な場所に移動）するために、さらに多くの移動が必要でした。



2048でうまくプレイした場合、結果がグラフの左下隅にグループ化され、それらのほとんどが青い点線の間にあると予測できます。 実際、ご覧のとおり、理想に到達することもありますが、結果はあまり安定していません。右上隅にかなりの数のポイントがあり、余分な動きとタイルがたくさんあります。



また、このグラフは、分析によって最小の予想移動数しか得られないという事実を強調しています。 運が良かったゲームがいくつかあり、927の動きと合計2076タイルの勝利を含め、938.8未満の動きで勝ちました（これは、選択の一番下の行の左から2番目の結果です）。誤って4



枚のタイルを手に入れました。また、余分な動きを必要とする重大なミスを犯さなかったためです。



原則として、わずか519の動きでゲームに勝つ可能性がある非ゼロの確率があります。 これを決定するには、チェーンを通過し、常にサイド4



への遷移を選択し、タイル2048を達成するために必要な遷移の数をカウントします。ただし、このような結果の確率は $$$0.1 ^ {521}$ 、または $$$10 ^ {-521}$ 。 私たちが観測している宇宙では、およそ $$$10 ^ {80}$ 原子なので、そのようなゲームがあなたに落ちるのを待つために息を止めてはいけません。 また、非常に不運で、常にタイル2



受け取る場合、わずか1032ムーブで勝つことができます。 そのようなゲームはより可能性が高く、その確率は $$$0.9 ^ {1034}$ ほぼ等しい $$$10 ^ {-48}$ 、したがって、おそらく、そのようなゲームは息を切らして待つ価値はありません。 タイル2



の出現確率はタイル4



の出現確率よりもはるかに高いため、平均938.8の移動は519よりも1032にはるかに近くなります。

おわりに

このパートでは、同一のタイルの結合が常に可能である場合の2048ゲームの進化をシミュレートするマルコフ連鎖を作成する方法を検討しました。 これにより、ゲームの興味深い特性を計算するためにマルコフ連鎖を吸収する理論の手法を適用することができました。特に、勝つには平均で少なくとも938.8の動きが必要であることがわかりました。



このアプローチを使用できるようにした主な単純化は、フィールド構造を無視することです。 つまり、タイルをバッグに落とし、フィールドには置かないことをお勧めします。 2番目の部分では、フィールドの構造を考慮する場合のケースを検討する予定です。 考慮する必要のある状態の数が何桁も大きくなることを学習しますが（おそらく、あなたが考えるほどではないかもしれませんが）、マルコフの意思決定プロセスの世界に入って、マルコフ連鎖の世界を離れなければならないことを理解します、これにより、プレイヤーの方程式に戻ることができます。 原則として、ゲームを完全に「解決」することができます。つまり、おそらく最適なプレイ方法を見つけることができます。

付録A：マルコフ連鎖分析

マルコフ連鎖を設定した後、数学の力を使用して、シミュレーションなしでその特性の計算を実行できます。 これらの計算の多くは、マルコフ連鎖が吸収マルコフ連鎖と呼ばれる特別な種類のマルコフ連鎖に属しているためにのみ可能です 。



吸収チェーンに関連するには、マルコフチェーンが次の基準を満たしている必要があります。

1. 少なくとも1つの吸収状態が必要です。 上で見たように、チェインには26の吸収状態があり、それぞれの勝ち状態に2048
   
   
   
   タイルがあります。
2. 任意の状態が有限数の遷移で吸収状態に到達できます。 これを決定する1つの方法は、吸収状態以外のチェーンにサイクルがないことを確認することです。吸収状態を除いて、チェーンは有向非循環グラフです。

遷移行列

吸収マルコフ連鎖があると判断したので、次のステップは、その遷移行列を標準形式で記述することです。 遷移行列は、上で定義した遷移確率を順序付けて、要素が $$$（i、j）$ 状態からの遷移の確率です $$$i$ 述べる $$$j$ 。



遷移行列へ $$$\ mathbf {P}$ 吸収回路 $$$r$ 吸収状態と $$$t$ 取り戻せない （つまり非吸収性）状態は正準型である可能性があり、4つの小さな行列に分割することが可能であるべきです $$$\ mathbf {Q}$ 、 $$$\ mathbf {R}$ 、 $$$\ mathbf {0}$ そして $$$\ mathbf {I}$ そのような：

$$

$$\ mathbf {P} = \ left（\ begin {array} {cc} \ mathbf {Q}＆\ mathbf {R} \\\ \ mathbf {0}＆\ mathbf {I} _r \ end {array} \右）$$

どこで $$$\ mathbf {Q}$ 行列です $$$t \ times t$ ある取消不能な状態から別の取消不能な状態に移行する確率を記述する $$$\ mathbf {R}$ 行列です $$$t \回r$ 非復帰状態から吸収状態への遷移の確率を記述する $$$\ mathbf {0}$ 行列を示します $$$r \ times t$ ゼロと $$$\ mathbf {I} _r$ 状態を吸収するための遷移行列です。これは単位行列です $$$r \回r$ 。



回路の遷移行列を標準形式に変換するには、状態の順序を決定する必要があります。 （1）状態が吸収されているか（吸収状態が最後であるか）に従って状態を並べ、（2）タイルの合計（昇順）で並べられ、最後に（3）字句順で依存関係を取り除きます。 これを行うと、次のマトリックスが得られます。











かなり大きい、つまりサイズ $$$3487 \回3487$ 、したがって、ズームアウトすると、ほぼ斜めに見えますが、右下隅をズームインすると、構造があることがわかります。特に、私たちが目指している標準的なビューがあります。

基本マトリックス

遷移行列の正準形を取得したら、それを使用して、チェーンの基本行列と呼ばれるものを見つけます。 これにより、テイクオーバー前に予想される遷移の数を計算できます。つまり、（最終的に！）元の質問に対する答えが見つかります。



基本マトリックス $$$\ mathbf {N}$ 比較的設定されています $$$\ mathbf {Q}$ アイデンティティ平等

$$

$$\ mathbf {N} = \ sum_ {k = 0} ^ {\ infty} \ mathbf {Q} ^ k \ mathbf {N} = \ sum_ {k = 0} ^ {\ infty} \ mathbf {Q} ^ k$$

どこで $$$\ mathbf {Q} ^ k$ 示す $$$k$ マトリックス度 $$$\ mathbf {Q}$ 。



アイテム $$$（i、j）$$$$\ mathbf {N}$ 一定の解釈があります：これは、状態に入る予想回数です $$$j$ 状態から始まるチェーンをたどる場合 $$$i$ 。 これを見るために、要素として $$$（i、j）$ 行列 $$$\mathbf{Q}$ 状態からの遷移の確率です $$$i$ 述べる $$$j$ 1つの遷移で、要素 $$$（i、j）$ 行列 $$$\mathbf{Q}^k$ 状態に入る確率です $$$j$ まさに $$$k$ 状態に入った後の遷移 $$$i$ 。 特定の状態のペアの場合 $$$i$ そして $$$j$ すべてについて述べた確率を要約します $$$k \geq 0$ 、状態に入る機会があるたびに金額が含まれます $$$j$ 状態の後 $$$i$、対応する確率で重み付けされており、希望する期待値が得られます。



幸いなことに、基本行列は、逆行列として、不快な無限の合計なしで直接計算できます。$$$\mathbf{I}_t - \mathbf{Q}$ どこで $$$\mathbf{I}_t$ 単位行列です $$$t \times t$ 。 つまり、 $$$\mathbf{N} = (\mathbf{I}_t - \mathbf{Q})^{-1}$ 。 （これの証拠は読者の宿題になります！）

勝つと予想される動きの数

基本行列を受け取った後、どの状態からの遷移の予想数を見つけることができます $$$i$ 行のすべての要素を合計することにより、吸収状態に $$$i$-言い換えれば、吸収状態に入る前の遷移の数は、途中で回復不能なすべての状態で行わなければならなかった遷移の総数に等しくなります。



ベクトルによって行列の積を計算することにより、すべての状態のこれらのシリーズの合計を一度に取得できます$$$\mathbf{N} \mathbf{1}$ どこで $$$\mathbf{1}$ 列ベクトルを示します $$$t$ 。 以来 $$$\mathbf{N} = (\mathbf{I}_t - \mathbf{Q})^{-1}$ 線形方程式を解くことでこれを行うことができます

$$

$$(\mathbf{I}_t - \mathbf{Q})\mathbf{t} = \mathbf{1}$$

のために $$$\mathbf{t}$ 。 アイテム $$$\mathbf{t}$ 初期状態に対応（空のセット $$$\left \{ \right \}$）、遷移の数です。この場合、結果の数値は939.8です。完了するには、減算するだけです$$$1$、初期状態からの移行は移動とは見なされないためです。これにより、最終的な答え-938.8の動きが得られます。



また、最小移動数の分散を次のように取得することもできます。

$$

$$2(\mathbf{N} - \mathbf{I}_t) \mathbf{t} - \mathbf{t} \circ \mathbf{t}$$

どこで $$$\circ$は、アダマールの（成分ごとの）積を示します。初期状態では、69.5の分散が得られ、8.3ステップの標準偏差が得られます。

付録B：分布曲線の形状

基本行列を使用して、マルコフ連鎖からの勝利への動きの分布の平均と分散の両方を計算できたことは注目に値します。しかし、ディストリビューションがこのような形式であることが判明した理由を知っておくといいでしょう。ここでの私のアプローチはおおよそのものです。しかし、それはシミュレーションからの経験的な結果と密接に一致し、いくつかの有用な情報を提供します。



先に行った観測に戻ることから始めます。フィールド上のタイルの合計は、遷移ごとに2または4ずつ増加します（初期状態からの最初の遷移を除く）。以下で説明するように、tileを取得するのではなく、フィールドで特定の量を取得することに関心がある場合2048



、二項分布を使用して必要な遷移数を計算するのは非常に簡単です。



ですから、次の質問はどれだけ受け取りたいかということです。上記のマルコフ連鎖の分析から、26の吸収（勝利）状態があると判断しました。また、それらは異なる「量の層」にあることもわかりました。つまり、私たちが目指している量は1つではなく、いくつかあります。各状態が吸収される確率を知る必要があります。それは吸収の確率と呼ばれます。次に、各吸収状態の吸収確率を合計の個別のレイヤーに要約して、特定の結果の合計で勝つ確率を見つけることができます。

吸収確率

幸いなことに、吸収確率は基本行列からも見つけることができます。特に、線形方程式を解くことでそれらを取得できます

$$

$$(\mathbf{I}_t - \mathbf{Q}) \mathbf{B} = \mathbf{R}$$

マトリックス用 $$$\mathbf{B}$ サイズ $$$t \times r$ その要素 $$$（i、j）$ 状態での吸収の確率です $$$j$ 状態から始まる $$$i$ 。前と同じように、初期状態から開始するときの吸収の確率に興味があります。吸収の確率のグラフを作成すると、15の吸収状態があり、その確率はグラフに表示するのに十分な大きさ（少なくとも$$$10^{-3}$ ）：











特に、ほとんどのゲームは終了または状態 $$$\left \{ 2,2,8,8,2048 \right \}$ 合計が2068年、または州別 $$$\left \{2,4,16,2048\right \}$ 、合計は2070です。層の合計ですべての吸収状態を合計すると、層の合計の完全な確率が得られます。

二項確率

目標を達成できる量があり、それぞれの目標を達成する頻度がわかったので、次の質問は次のとおりです。特定の量を得るために必要な動きはいくつですか。上記のように、二項分布に関連してこの問題を認識できます。これにより、特定の数の「試行」から特定の数の「成功」の確率を計算できます。



この場合、「試行」とは移動を意味し、「成功」とはゲームがタイルを与える移動を意味し4



ます。上記のように、これは0.1の確率で発生します。ここでの「失敗」とは、ゲームがタイルを与える動きであり、2



0.9の確率で起こります。



この成功の解釈を考えると、与えられた量を得るために$$$S$ のために $$$M$ 必要な動き $$$\frac{S}{2} - M$ からの成功 $$$M$ 動きます。 これは、各移動が少なくとも追加するために発生します $$$2$ それは一般的に与える $$$2M$ 、各成功は追加の量に追加されます $$$2$ 一般的に貢献 $$$2 \left(\frac{S}{2} - M\right) = S - 2M$ 。 これらの値を追加すると、必要な量が得られます $$$S$ 。



次に、金額を取得する共同確率 $$$S$ 移動回数 $$$M$ 二項であり、特に

$$

$$\mathrm{Pr}(M=m, S=s) = B\left(\frac{s}{2} - m; m, 0.1\right)$$

どこで $$$B(k; n, p)$ は二項分布の質量分布関数であり、正確に取得する確率を与えます $$$k$ の成功 $$$n$ 成功の確率が $$$p$ 、つまり

$$

$$B(k; n, p) = {n\choose k}p^k(1-p)^{n-k}$$

どこで $$$n \choose k$は二項係数を示します。



目標額がわかったので$$$S$、私たちが努力しているので、関心のある金額が共同分配からのものであるという事実を考慮して、動きの条件付き分布を計算できます。つまり、見つけることができます$$$\mathrm{Pr}(M | S)$ どうやって

$$

$$\mathrm{Pr}(M | S) = \frac{\mathrm{Pr}(M, S)}{\mathrm{Pr}(S)}$$

どこで $$$\mathrm{Pr}(S)$ 加算により共同分布から取得 $$$M$ あらゆる可能な量に対して $$$S$ 。 それは注目に値する $$$\mathrm{P}(S)$ゲームはタイルを与えることで金額を「スキップ」する可能性が常にあるため、可能な金額ごとに1未満です4



。



各目標量についてこれらの条件付き分布をすべて受け取ったので、それらを加算して、目標量の総吸収確率で重み付けし、総確率を取得することができます。これにより、シミュレーションの分布とかなり正確に一致します。











ここでは、シミュレートされた分布は灰色の列で示され、色付きの領域は各条件付き分布を示しています。各条件付き分布は、その合計の吸収の合計確率に従ってスケーリングされ、平均してより多くの量がより多くの動きを必要とするため、いくつかの動きによってシフトされます。



この結果の1つの解釈：最適なゲームでは、勝つための動きの数は、プレイヤーが2048タイルを収容するのに十分な大きさをどれだけ早く取得できるかに依存し、それ4



は二項分布に続くタイルの数に依存します。

---

この記事の下書きを編集してくれたHope ThomasとNate Stemenに感謝します。

注釈

1. , , . .
2. : , 2
   
   
   
   , , , 4
   
   
   
   , 8
   
   
   
   .
3. dot
   
   
   
   graphviz . dot
   
   
   
   , .
4. 「You win！」画面の外観は、このデータを収集する数か月にわたって数回変化しました。記録のために：これらすべての月の間、私は2048年にプレーしただけではありません。

パート2.組み合わせを使用した状態のカウント

前のパートで、2048ゲームに勝つには平均で少なくとも938.8の移動が必要であることがわかりました。これらの計算を実行できるようになった主な単純化は、フィールドの構造を無視したことです-本質的に、タイルをフィールドに置くのではなく、バッグに投げ入れました。この「バギング」された単純化のおかげで、3486州のみのマルコフ連鎖の形でゲームをシミュレートすることができました。



このパートでは、「バッグ」を単純化せずに状態の数を計算する最初の試みを行います。つまり、この部分では状態フィールドの完全な構成が含まれ、フィールドの各セルに存在するタイルが決定されます。したがって、タイル（およびタイルのないセル）の位置が含まれるので、このタイプの状態がはるかに多くなることを期待する必要があります。後で見るように、それはまさにそうです。



これを行うために、列挙型コンビナトリクスの（単純な）テクニックを使用して、たとえば上記で説明したように、ゲームでは発生できない書き込み可能な状態を除外します。結果は、2048に類似したすべてのゲーム、さらには（4x4だけでなく）他のフィールドでプレイされたゲームや他のタイル（2048



）小さいフィールドや小さいタイルでのこのようなゲームの状態は、2048年の完全な4x4ゲームよりもはるかに少ない状態であり、ここで使用される手法は、小さいフィールドサイズで予想される条件の数を減らすのに比較的効果的であることがわかります。ボーナスとして、4x4フィールドがタイルに到達できる最小の正方形フィールドであることもわかり2048



ます。グラフの実装またはコードを評価したい場合、



この部分のベースとなる（研究品質の）コードはオープンソースです。

ベースライン

2048ゲームの状態数を推定する最も明白な方法は次のとおりです。16個のセルがあり、各セルは空にするか、値が2の11の累乗（2から2048）のいずれかであるタイルを含むことができます。セル、つまり合計 $$$12^{16}$ 、または184兆（およそ $$$10^{17}$）この方法で記述できる値。比較のため：いくつかの推定によると、チェス盤上の位置の可能な構成の数はほぼ等しい$$$10^{45}$、最近の推定によると、ゲームでは$$$10^{170}$ 状態なので、少なくとも $$$10^{17}$-これはたくさんありますが、これはゲームの記録ではありません。



より一般的な形式では、このような2048ゲームは次のように表すことができます。$$$B$ フィールドのサイズであり、 $$$K$ -値を持つ勝利タイルの程度 $$$2^K$ 。 便宜上、 $$$C$ フィールド内のセルの数、つまり $$$C=B^2$ 。 4x4フィールドを持つ通常の2048ゲームの場合： $$$B=4$ 、 $$$C=16$ 、そして $$$K = 11$ なぜなら $$$2^{11} = 2048$ 、および可能な状態数は

$$

$$(K + 1)^C$$

次に、考えられる意味を明確にする方法を見てみましょう。



まず、タイルを取得するとゲームが終了するため$$$2^K$、このタイルがどこにあり、それ以外のフィールドに何があるかは気にしません。したがって、すべての状態をタイルと組み合わせることができます$$$2^K$「勝利」という特別な状態にあります。他の状態では、各セルは空であるか、タイルの1つを含むことができます$$$K - 1$ 。 これにより、関心のある条件の数が減ります

$$

$$K^C + 1$$

どこで $$$1$-これは「勝利」の状態です。



第二に、これらの条件のいくつかに気づくことができます$$$K^C$ゲームで発生することはありません。特に、ゲームのルールは2つの有用なプロパティを意味します。



プロパティ1：フィールドには常に少なくとも2つのタイルがあります。



プロパティ2：フィールドには常に少なくとも1つのタイル2



またはタイルがあります4



。



最初のプロパティは尊重されます。なぜなら、2つのタイルでゲームを開始し、それらを結合しても、まだ1つあり、その後、ゲームはランダムなタイルを1つ追加し、2つ存在するからです。ゲームは常に移動後にタイル2



またはタイルを追加するため、2番目のプロパティが尊重され4



ます。



したがって、正しい状態では、フィールド上に少なくとも2つのタイルが必要であり、そのうちの1つはタイル2



またはタイルでなければなりません。4



。これを考慮するために、タイル2



なしまたはタイルなしのすべての状態を減算できます4



。$$$(K-2)^C$、1つのタイル2



と残りの空のセルのみを含む状態、$$$C$、1つのタイル4



と残りの空のセルのみを含む状態、$$$C$ 。 考えられる意味を与えてくれます。

$$

$$K^C - (K-2)^C - 2C + 1$$

状態。 もちろん、いつ $$$K$ または $$$C$ 素晴らしいですね $$$K^C$、つまり、主な用語ですが、小さな値の場合、この調整はより重要です。



この式を使用して、さまざまなサイズのフィールドと最大タイルの可能な状態数を減らしましょう。

最大タイル	フィールドサイズ
	2x2	3x3	4x4
8	73	19 665	43,046.689
16	233	261 615	4,294,901,729
32	537	1 933 425	152544 843 873
64	1,033	9 815 535	2 816 814 940 129
128	1,769	38 400 465	33 080 342 678 945
256	2 793	124 140 015	278 653 866 803 169
512	4 153	347 066 865	1 819 787 258 282 209
1024	5 897	865 782 255	9718525 023 289 313
2048	8 073	1 970 527 185	44 096 709 674 720 289

2x2と3x3のフィールドを持つゲームでは、4x4のゲームよりも状態がはるかに少ないことがすぐにわかります。さらに、4x4ゲームで使用可能なタイルの数を2048“オンリー” 44兆個、または〜$$$10^{16}$ 。

レイヤーで数える

：状態のこれらの数をもう少し理解するために、我々は、前のセクションに有用である、もう一つの重要な特性を使用することができます



プロパティ3：各ターン2または4にフィールド増加のタイルの合計



このルールが観察され、2枚のタイルの労働組合ので、フィールド上のタイルの量は変更されません。その後、ゲームは2



またはを追加します4



。



プロパティ3は、ゲーム中に状態が繰り返されないことを意味します。これは、タイルの合計によって状態をレイヤーにソートできることを意味します。ゲームが合計10の層の状態にある場合、次の状態は合計12または14の層にあることがわかります。各層の状態の数も計算できることがわかります。



させる $$$S$フィールド上のタイルの量を示します。その方法の数を数えたい$$$C$ それぞれが2から2の累乗です $$$2^{K-1}$ 取得するために折り畳むことができます $$$S$ 。



幸いなことに、これは組合せ論のよく研究問題の一種である：カウント曲整数。一般に、整数の構成$$$S$ 合計する整数の順序付けられたコレクションです $$$S$ ;集合体の各整数はpartと呼ばれます。たとえば、整数$$$3$ すなわち、4つの構成があります $$$1 + 1 + 1$ 、 $$$1 + 2$ 、 $$$2 + 1$ そして $$$3$ 。たとえば、2のべき乗や一定数のパーツの存在など、パーツに制限がある場合、そのような構成はlimitedと呼ばれます。



さらに幸いなことに、Chinn and Niederhausen（2004）¹はすでにこのタイプの限られた構成のみを研究しており、再帰を開発して、各部分が2の累乗である特定の数の部分がある構成の数を計算できるようにしました。させる $$$N(s, c)$ 全体の構成（正）の数を示します $$$s$ まさに $$$c$ パーツ。各パーツは2の累乗です。 それから

$$

$$N(s, c) = \begin{cases} \sum_{i = 0}^{\lfloor \log_2 s \rfloor} N(s - 2^i, c - 1), & 2 \le c \le s \\\ 1, & c = 1 \textrm{, } s \textrm{ - 2} \\\ 0, & \textrm{ } \end{cases}$$

なぜなら、それぞれの構成のために数字 $$$s - 2^i$ で $$$c - 1$ 構成を取得できる部分 $$$s$ から $$$c$ パーツ、値を持つ1つのパーツを追加 $$$2^i$ 。



ここで、合計の境界に小さな変更を加える必要があります。2から始まる2のべき乗を使用する必要があります。 $$$2^{K-1}$ タイルがある場合 $$$2^K$その後、ゲームに勝ちます。これを行うには、$$$N_m(s, c)$ 番号構成の数を示します $$$s$ まさに $$$c$ パーツ。各パーツは2の累乗です。 $$$2^m$ 前に $$$2^{K-1}$ 。 上記のロジックにより、これは次の方程式で定義できます。

$$

$$N_m(s, c) = \begin{cases} \sum_{i = m}^{K - 1} N(s - 2^i, c - 1), & 2 \le c \le s \\\ 1, & c = 1 \textrm{, } s = 2^i \textrm{ } i \in \{ m, \ldots, K-1 \} \\\ 0, & \textrm{ } \end{cases}$$

これで、 $$$c$ パーツですが、パーツがアップするように数式が必要です $$$c$ 。 前のセクションと同じ推論を使用できます。タイル2または4のない状態を減算します。 $$$N_3(s, c)$ 。 プロパティ1によると、少なくとも2つの部分が必要なので、次のように要約し始めます。 $$$c=2$ 。 これにより、合計を持つ状態数の可能な値として与えられます $$$s$

$$

$$\sum_{c = 2}^{C} {C \choose c} \left( N_1(s, c) - N_3(s, c) \right)$$

ここに $$$C \choose c$選択肢の数を与える二項係数です$$$c$ 可能性の $$$C$タイルが配置されるセル。それらをチャートにマークしましょう。









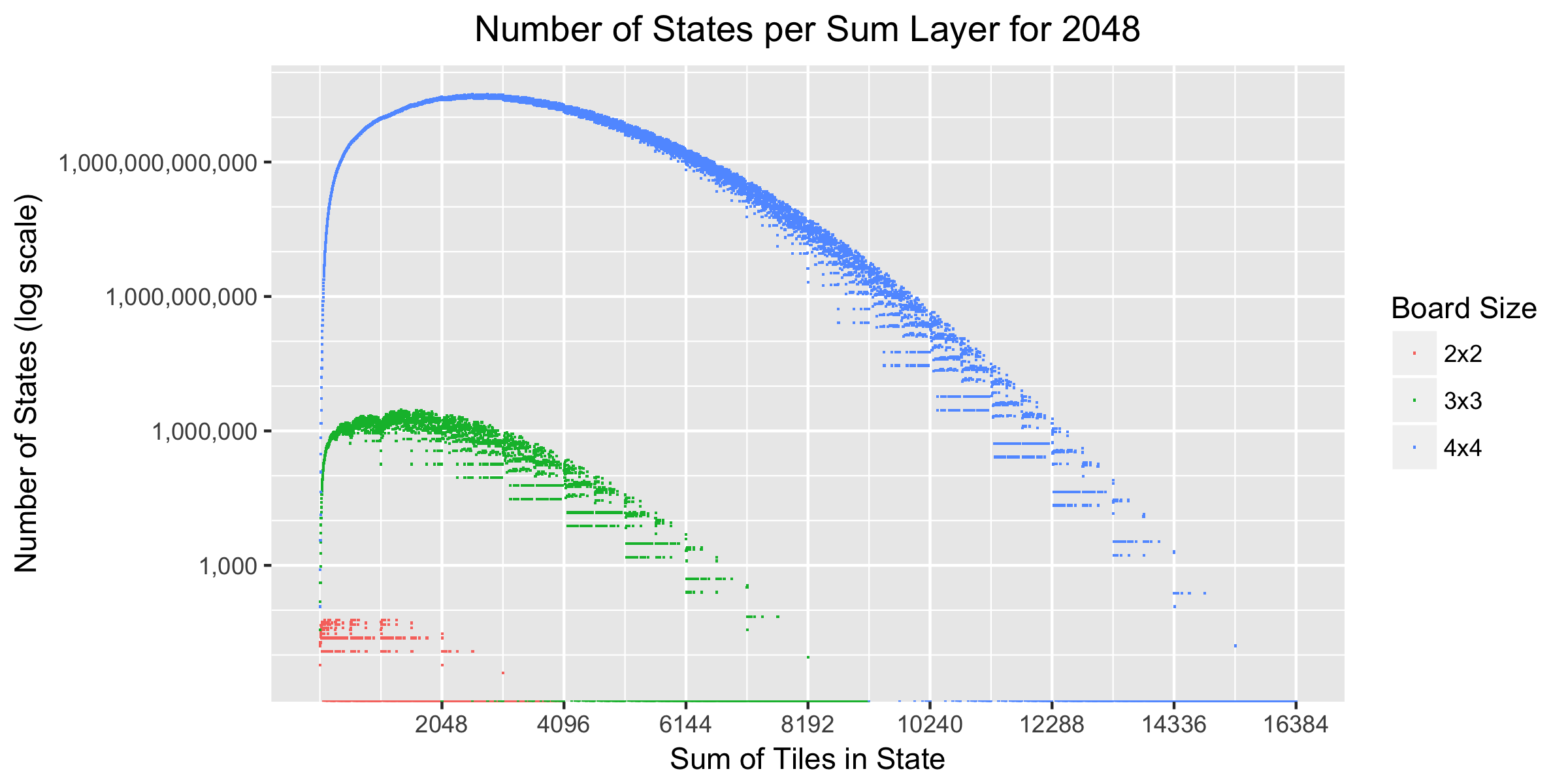
順序に関しては、2x2ゲームではレイヤーあたり60ステートを超えることはなく、3x3ゲームではレイヤーあたり最大約300万ステート、4x4ゲームでは最大約32兆（ $$$10^{13}$）レイヤーごとの状態。州の数はゲームの初期段階で急速に増加しますが、その後、フィールドがいっぱいになると速度が低下し、徐々に減少します。曲線の減少部分では、特に大量にギャップが見られます。これは、フィールドに適合するタイルが存在せず、この値で合計される場合に発生する可能性があります。



水平軸の上限は、$$$C$ それぞれの値は $$$2^{K-1}$ 、つまり、達成可能な最大量は $$$C 2^{K-1}$、または2048までの4x4ゲームの場合は16,384です。



最後に、4から4までのレイヤーのすべての可能な合計にわたって各レイヤーの状態の数を合計する場合、注目に値します$$$C 2^{K-1}$そして、特別な勝利状態に1つを追加すると、前のセクションで予想されたのと同じ数の状態を取得します。これは、推論の正しさを調べるのに役立つテストです。

レイヤーの到達可能性

プロパティ3のもう1つの有用な結果は、2つの連続するレイヤーに状態がない場合、後のレイヤーに到達できないことです。これは、ターンごとに最大4ずつ量が増加する可能性があるためです。状態のない2つの隣接するレイヤーがある場合、合計は次のレイヤーに「ジャンプ」するために1回の移動で6増加しますが、これは不可能です。したがって、上記の計算を使用して状態を含まない層の合計を見つけると、最後の到達可能な層の後に到達不能な層の状態を除外することにより、可能な値を絞り込むことができます。到達可能なレイヤーの最高の合計（到達不能なタイルなし2048



）：

フィールドサイズ	最大達成可能層量
2x2	60
3x3	2,044
4x4	9,212

この表は、合計60以下のレイヤーに32



タイル64



を表示できないため、2x2フィールドで達成できる最大タイルがtileであることも示しています。同様に、3x3フィールドの最大到達可能タイルはtile 1024



です。これは、4x4フィールドがタイル2048



²に到達できる最小の正方形フィールドであることを意味します。4x4フィールドの場合、タイルに到達する前に2048



（つまり、勝利なしに）到達できるレイヤーの最大量は9,212ですが、タイルが解決される2048



と、より多くの量を達成できます。



レイヤーの到達可能性を考えると、状態数の新しい可能な値は次のようになります。

最大タイル	方法	フィールドサイズ
		2x2	3x3	4x4
8	ベースライン	73	19 665	43,046,689
	レイヤーの到達可能性	73	19 665	43,046,689
16	ベースライン	233	261 615	4,294,901,729
	レイヤーの到達可能性	233	261 615	4,294,901,729
32	ベースライン	537	1 933 425	152 544 843 873
		529	1 933 407	152 544 843 841
64		1 033	9 815 535	2 816 814 940 129
		905	9 814 437	2 816 814 934 817
128		1 769	38 400 465	33 080 342 678 945
		905	38 369 571	33 080 342 314 753
256		2 793	124 140 015	278 653 866 803 169
		905	123 560 373	278 653 849 430 401
512		4 153	347 066 865	1 819 787 258 282 209
		905	339 166 485	1 819 786 604 950 209
1024		5 897	865 782 255	9 718 525 023 289 313
		905	786 513 819	9 718 504 608 259 073
2048		8 073	1 970 527 185	44 096 709 674 720 289
		905	1 400 665 575	44 096 167 159 459 777

これは2x2フィールドに大きな影響を与え、ゲームの状態数を8,073から905に2048に減らします。2x2フィールドで32



より多くのタイルを達成することは不可能であるため、到達可能な状態数の値はその後の最大タイルの905から増加しないことに注意してください32



。また、3x3フィールドにわずかに影響しますが、4x4には比較的小さな影響があります。ゲームの場合、合計で約5,000億の状態を2048まで取り除きます



。グラフィック形式では、このデータは次のようになります。

おわりに

2048ゲームと、より小さなボードとより小さな最大タイル上の同様のゲームの状態数の大まかな見積もりを取得しました。これまでのところ、4x4ゲームの2048までの状態数の最良の推定値は約44兆（〜$$$10^{16}$ ）



多くの理由でゲームで達成できない条件を考慮に入れることができるため、この見積もりやその他の見積もりは大幅に誇張されている可能性があります。たとえば、記事のこの部分のイラストからタイトルまでの状態：









私たちが調べたすべての制限を満たしますが、ゲームでそれを達成することはまだ不可能です：それに入るには、タイルをある方向に移動する必要があり、2つのタイル2



をフィールドの端に移動します。おそらく、これを念頭に置いて上記の計算引数を微調整する方法があるでしょう（そして、おそらく、他の制限に合わせて）。しかし、今のところ、これを行う方法がわかりません。



次の投稿では、真に達成可能な状態の数がはるかに少なく、実際にそれらをリストしていることがわかります。3x3と4x4のフィールドにはまだ多くの機能があるので、数学だけでなく情報処理理論の知識も必要です。

---

この時点まで読んだことがあるなら、Twitterで私をフォローする価値があるかもしれませんし、Overleafで採用リクエストを送ってくれるかもしれません。

注釈

1. Chinn, P. and Niederhausen, H., 2004. Compositions into powers of 2. Congressus Numerantium , 168, p.215. ()
2. , , , 2048
   
   
   
   . , , . , , , 4x4 131072
   
   
   
   ( $$$2^{17}$ ), . — , , . , - , 8192
   
   
   
   , « » 131072