🏮 ☦️ 👮 機械学習における予測の品質を向上させるための隠れたデータ依存関係の特定 👨‍🔬 🤟🏾 👨🏼‍🎓

記事の概要

問題の声明。
問題の正式な説明。
タスクの例。
非表示の線形依存関係を持つ合成データのいくつかの例。
他の隠された依存関係がデータに含まれている可能性があります。
依存関係検索を自動化します。

記号の数がしきい値を下回っています。
記号の数がしきい値を超えています。

問題の声明

多くの場合、機械学習では、データがアプリオリに収集される状況があり、その場合にのみ特定のサンプルを既知のクラスに分割する必要があります。その結果、既存の機能セットが効果的な分類に適していない場合に、状況が発生することがよくあります。少なくとも最初の近似として。

このような状況では、個々に機能が弱いメソッドの構成を構築することも、機能間の隠れた関係を明らかにすることでデータを充実させることから始めることもできます。そして、見つかった依存関係に基づいて、新しい機能のセットを構築します。その一部は、分類の品質を大幅に向上させる可能性があります。

問題の正式な説明

n個の実数で定義されたL個のオブジェクトを分類するタスクに直面しています。クラスラベルが-1と+1の場合、単純な2クラスのケースを考えます。私たちの目標は、線形分類器、つまり-1または+ 1を返す関数を構築することです。さらに、特徴記述のセットは、特定の特徴セットで測定された反対クラスのオブジェクトに対して、コンパクト性仮説が実際に機能せず、分離超平面が非常に構築されるようなものです非効率的。

つまり、オブジェクトの特定のセットに関する分類問題を効率的に解決できないかのように見えます。

したがって、数値-1または1を含む応答列と、L行とn列で構成される属性値X1 ... Xnの対応するマトリックスがあります。

私たちは、分類されたオブジェクトの新しい機能として機能し、最適な分類子を構築するのに役立つ可能性のあるこのような依存関係F（Xi、Xj）を見つけるタスクを設定しました。

タスクの例

例を使用して関数F（Xi、Xj）を見つける問題を見てみましょう。もちろん、非常に重要です。

例はレプラコーンに関連付けられます。レプラコーンは、誰かが知らない場合、私たちの近くのどこかに存在しますが、ほとんど誰も見ませんでした。そして、彼らは、人々のように、自分のコンピューター、インターネット、ソーシャルネットワークを持っています。ほとんどの場合、彼らは金を探してバッグに保管することに専念しています。しかし、正直なレプラコーンに加えて、この重要な仕事から脱却しようとしている人もいます。それらは反体制的レプラコーンと呼ばれます。そして、レプラコーンの金の量の増加率が望ましい値に達することができないのは、まさにそれらのためです！

レプラコーンの世界にも機械学習があるため、彼らは大規模なソーシャルネットワークでの行動に基づいてそれらを見つけることを学びました。しかし、問題があります！毎年多くの若いソーシャルネットワークが市場を獲得しようとしていますが、それでも分析のためにユーザーに関する十分なデータを収集することができません！そして、彼らが収集するデータは、まともなレプラコーンと反抗的なレプラコーンを区別するのに十分ではありません！そしてここでは、利用可能な機能の説明で隠れた依存関係を探す必要があるため、一見しただけでは不十分なデータに基づいて、最適な分類器を構築できます。

ただし、ソーシャルネットワークの例はおそらく複雑すぎて解析できないため、核レプラコーンプロセッサの例で同様の問題を解決してみましょう。それらは4つの主要な機能によって特徴付けられます：

a）反応器の回転速度（百万rpm）

b）計算能力（兆回の計算/秒）

c）負荷時の反応器の回転速度（百万rpm）および

d）負荷時の計算能力（兆回計算/秒）

核処理業者は、2つの主要企業（0と1（「Black Zero」と「The First」））によって生産されています。同時に、Black Zeroの価格は半額ですが、リソースも5倍低くなっています！ただし、主な状態。核処理業者のサプライヤーは、常に顧客を欺き、The Firstマシンにお金を支払う代わりに、安価で信頼性の低いBlack Zeroマシンを供給しようとしています。同時に、原子炉の運転パラメータの変動は非常に大きいため、ほとんどの測定の主な特性に応じて区別することはできません。表1は、各企業に対してランダムに選択された50台のマシンの特性を示しています。

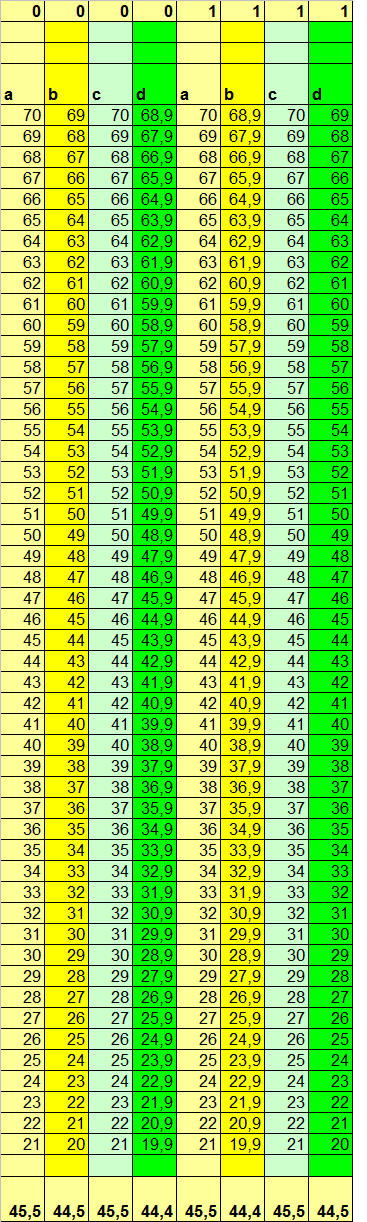
表1

比較の便宜上、クラス1とクラス0のオブジェクトは垂直方向ではなく、相互に関連する側に配置されます。上記の例では、一般的に、計算能力のパラメーターは原子炉の速度に依存し、異なるメーカーの機械では多少異なることがわかります：Black Zero機械では、通常の条件下では、類似の原子炉速度での計算数は最初の機械に比べて多くなりますが、負荷の下で。もちろん、これは、The Firstマシンが負荷なしでプラズマ節約モードに入り、パフォーマンスがわずかに低下するためです。しかし、負荷がかかると、彼らは明らかに競合他社の先を行きます。

この依存関係が見えるのは、データが特別に選択されているためです。実際には、この発明の例のように美しく分類できない数千の次元と数十（数百ではないにしても）の標識の中で、そのような目で依存関係を見るのは通常不可能です。そして、各機能のビジネス全体の特異性がまだ完全に明確でない場合、目でそのようなパターンを見つけようとすることは、少なくともパフォーマンスの低い活動です。

したがって、アルゴリズムを学習する自動化のパラダイムのフレームワーク内で移動して、最大の属性間の依存関係を見つけるプロセスからヒューマンファクターを除外したいと思います。非表示の依存関係のいくつかのオプションを見て、それらを検出するプロセスを整理する最善の方法を考えてみましょう。

非表示の線形依存関係を持つ合成データのいくつかの例

依存関係のバリアント1。Xj= K * Xi + C、K = 1

依存関係の最初のバリアントは、オブジェクトのj番目の符号はi番目の符号、および定数で表される自由項に線形に依存します。

狭い例では、比例係数は1に等しくなるため、自由項の寄与を確認する方が適切です。

クラス0ではb = a-1、d = c-1.1とし、クラス1ではその逆です（b = a-1.1、d = c-1）

この場合、もちろん、値を持つ新しい列が

（d-b）

それぞれ0および1クラスのオブジェクトの値を提供します

（c-1.1）-（a-1）= c-a-0.1

そして

（c-1）-（a-1.1）= c-a + 0.1

それに応じて。そして、これは、列Aと列Cのデータの均一性を考えると（そしてこれがタスクの条件の1つです）、オブジェクトを分離するための優れたツールを提供します。そして、少なくとも、この新しい列が最終的な分類に積極的に貢献していることを期待できます。

このような計算の結果は、発明されたデータで表2に見ることができます。

表2

同様の状況は、一見非常に引き締まっているように見えますが、実際には人生で起こります。例としては、一定の副作用を伴う一連の規制されたアクションを実行するために特定の条件を実装する必要があります。この例の核プロセッサーの場合、一定の計算能力の低下は、負荷のかかった状態で仕事をするために固定プロセスを開始する必要性に関連している可能性があります。人生では、追加の発電機の立ち上げ、資源の予備への固定配分、火力発電所の内燃機関または産業用発電機を始動するためのエネルギーなど。

ただし、実際の問題でこの特定の関数F（d、b）を選択することは確かに明らかではありません。したがって、まず、F（Xi、Xj）の異なる選択がどのような結果をもたらすかを考えてみましょう。

F(Xi, Xj) = Xi/Xj

タスクの属性の観点から言えば、ここでは、たとえば負荷時の計算能力の低下（B / D）を測定することができます。さらに、そのような劣化は定数に依存せず、完全に相対的な値であるという仮定に基づいています。

結果として何が起こるか見てみましょう。

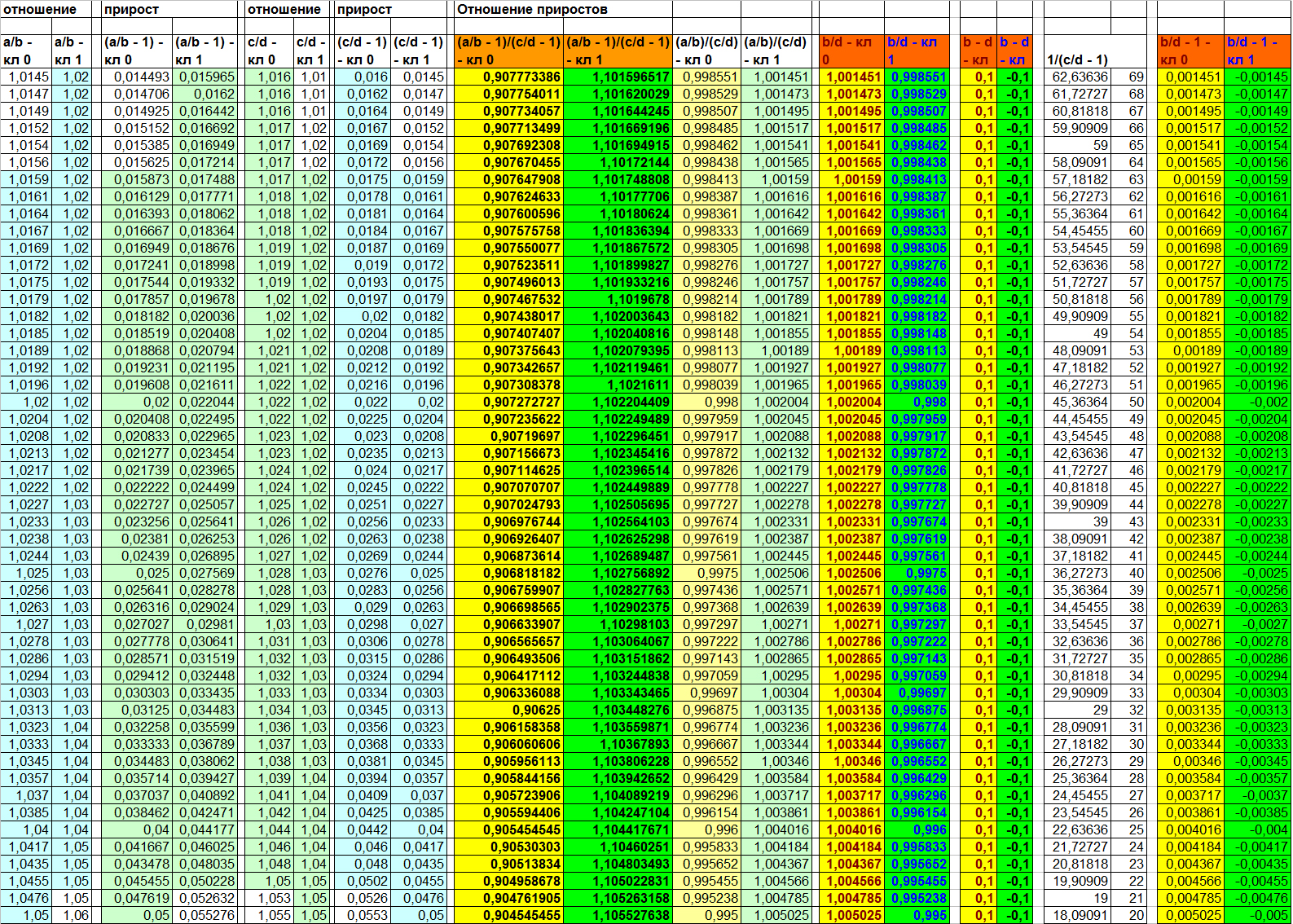
表3

表3に見られるように、関係（A / B）と（C / D）は有益ではありません。それらの反対のクラスのオブジェクトはまだ非常に混合されています。しかし、B / D比は、サンプルを線形分離可能にすることが期待されます。（B-D）の場合と同じです。ただし、少し先を見て、この属性によるこの線形分離可能性の理由は、差分関数の場合とまだ多少異なると言います。これは、次の例で明確にわかります。

それまでの間、このニュアンスを下げて、この依存関係のバリエーションで何が間違っているのか考えてみましょう。アルゴリズムの場合-ほとんどありません。しかし、両方のクラスの視覚的なサインは非常に近いように思えるかもしれません。もちろん、この例では、すべての値がユニットのさまざまな側面に美しく分散されていますが、人生ではこの明確さが存在しない場合があります。この表面的な問題を解決するには？ 1つの簡単なオプションは、分母の値に対する分子の増分を計算することです。これはどういう意味ですか？

比率（X / Y）を計算すると、「YがXの値に何回収まるか」という質問に対する答えが得られます。ただし、「Xを取得するためにYの値にいくつのY-sを追加する必要があるか」という質問を解決する方が有利な場合があります。 2番目のケースでは、成長を探しています。成長は正と負になり、単純な式（X / Y-1）で表されます。 1つのマイナスがあります-測定単位として1つのYを使用するためです。

再び表3（最も右側の2つの列）を見て、異なるクラスのオブジェクトの増加が異なる兆候であることを明確に確認できることに注目してください。したがって、異なるクラスのDからBの多方向の成長について話すことができます。そして、この場合、（B / D）機能がサンプルを線形分離可能にするという事実で実際に重要な役割を果たすのは、まさにこの場合です。結論：各関数：（B-D）および（B / D）（またはB / D-1）は、サンプルをわずかに異なる方法で線形分離可能にします。つまり、特定の属性ペアに対して生産性が高いのはそのうちの1つだけである場合があります。しかし、これについては後で詳しく説明します。次に、3番目の関数に移りましょう-最初の例の最後の関数です。

（A / B）/（C / D）-線形関係比

または

（A / B-1）/（C / D-1）-成長率

線形関係または増分関係を検討する動機は何ですか？機器の2つの異なるメーカーの例では、このような計算には次の意味があります。「負荷が接続されている場合、生産性の速度依存性はどれだけ変化するか」。

まあ、それは正当な質問です。さまざまなメーカーについて話していることを考えると、負荷の増加に伴う機器のさまざまな動作が予想されます。人生の状況では、F（Xi、Xj）とF（Xii、Xjj）の2つの関係があり、それぞれが実際には未知のパラメーターセットの関数であるという事実について話すことができます：F（M）とF '（M）。そして、この仮説が当てはまる場合、関数FおよびFのそれぞれが異なるクラスのオブジェクトに対して等しく現れる場合でも、その構成F ''（F、F '）は異なるクラスのオブジェクトに対して異なるように現れることがあると仮定できます。これらの異なるクラスの現実は、集合Mからの未知のパラメーターに対して著しく異なります。

もちろん、この例では、データを適切にコンパイルしたため、この2次関係のレッグがどこから来たかを最初に知っています。人生では、私たちはこれを知らず、そのような関係が存在するという事実のみに依存するかもしれません。したがって、彼女を見つけようとします。

表3（中央の4つの列）に戻り、これらの関数がペア（A / B）と（C / D）でどのように機能するかを見てみましょう。どちらもサンプルを線形分離可能にすることがわかります。前述のとおり（B-D）および（B / D）。

この例の唯一の重要な違いは、関数（A / B）/（C / D）の値が互いに非常に近いが、関数（A / B-1）/（Cを使用するときのオブジェクトの分割ストリップの幅/ D-1）ははるかに広いです。そのような結果を見て、次の2つの質問をすることができます。

この違いは重要ですか？
両方の機能は常に同じ分離力を示していますか？

最初の質問への答え：はい、構成にメトリック分類方法を含めるために何らかの方法を計画する場合。実際、幅の広い分割ストリップでは、コンパクトな仮説の方がうまく機能します。さらに、視覚化の品質について話すことができます。もちろん、この例では、トレーニング後のメトリックメソッドは、（A / B）/（C / D）属性に基づいてサンプルを正確に共有することに注意してください。ただし、実際には、メトリックを使用する場合の相互侵入ははるかに重要です。

この例の2番目の質問に対する答えは、おそらく十分に明白ではありません。次の例を検討するまで、宙に浮いたままにしておきましょう。

依存バリアント2. Xj = K * Xi + C、K = 1、C-両方のクラスのワンサイン

この例は前者の特殊なケースであり、自由条件はすべてのオブジェクトに対してゼロより大きい値またはゼロより小さい値を取ります。これがどのような効果をもたらすかを見てみましょう。

両方のクラスでb = a-1、ただしクラス0ではd = c-1.2、クラス1ではc-1.3とする）

この場合、もちろん、値を持つ新しい列が

（B-D）は、それぞれ0および1クラスのオブジェクトの値を提供します

（c-1）-（a-1.2）= c-a + 0.2

そして

（c-1）-（a-1.3）= c-a + 0.3

それに応じて。そして、これは、列Aと列Cのデータの均一性を考えると（そしてこれがタスクの条件の1つです）、オブジェクトを分離するための優れたツールを提供します。繰り返しになりますが、少なくとも、この新しい列が最終的な分類に積極的に貢献していることを期待できます。

このような計算の結果は、発明されたデータで表4に見ることができます。

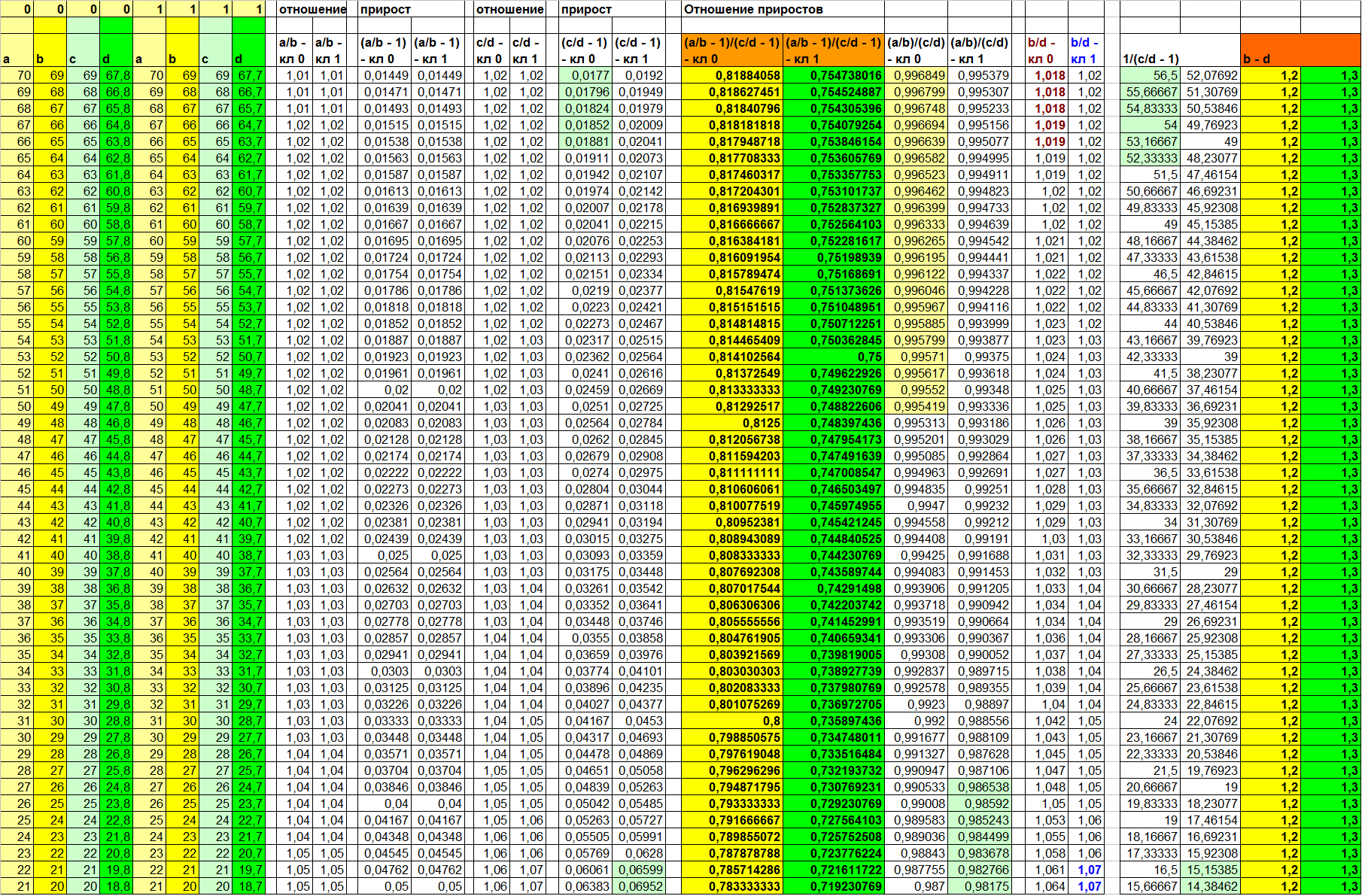
表4

左側の8列は、クラス0および1の符号a、b、c、dの実際の値です。残りの列の値は、ヘッダーの関数に従って計算されます。 2つの右側の列の値（B-D）。

それでは、例1で選択を線形分離可能にすることができた既知の関数を使用する理由を見てみましょう。

F(Xi, Xj) = Xi/Xj

表4からわかるように、この場合の有益な関係は見つかりません。また、さまざまな方法で計算した値である列の比率（B / D）でも、満足のいく結果は得られません（右側の5番目と6番目の列）。しかし、問題は何ですか？無料会員の意味を少し変更しました！その理由は、最初の例では、さまざまなクラスの無料メンバーの記号が異なるためです。そして、これがまさにサンプルを特性上で直線的に分離可能にしたものです（B / D）。

（A / B）/（C / D）-線形結合の比率または

（A / B-1）/（C / D-1）-成長率

レプラコーンコンピューターに関する先入観のある例では、この計算は理にかなっていることを思い出してください。「負荷がかかった状態での生産性の速度への依存度はどれくらいか」。

特別に調整およびソートされたデータでは、負荷がかかった状態でのパフォーマンスの低下が、The Firstマシンの方がBlack Zeroマシンよりもわずかに高いことが肉眼でわかります。（しかし、なぜそれがより高価なのでしょうか？明らかに、Black Zeroは信頼性を維持しながら、核プロセッサーを引き出せるよりも多く搾り取ろうとしています。したがって、彼らは最初のプロセッサーより5倍少ないサービスを提供します！マーケティングのために、Black Zero！）

さて、私たちの関係に戻りましょう。もう一度表4を見ると、非常に興味深いことが1つわかります。

増分比（A / B-1）/（C / D-1）はサンプルを線形分離可能にしますが、線形関係（A / B）/（C / D）の比率はかなり大きな範囲の不確実性を残します！ところで、「両方の機能は常に同じ分離能力を示していますか？」という質問に対する答えがここにあります

（表4では、これらは右側の7番目から10番目の列です。重複しない値が強調表示されています）

じゃあ 3番目の例に移りますが、今のところは次のことを覚えておいてください。

線形関係と成長関係の関係の関数は、常に同じ分割能力を示すとは限りません。
この例では、成長率関数の分離能力が線形関係関係関数の分離能力よりも高い場合、差関数も100％の分離能力を示しましたが、属性のペアの関係は最適な分類子を構築するのにあまり有益ではありませんでした。

依存関係のバリアント3. Xj = K * Xi + C、K！= 1、C = 0

別の特別なケースですが、自由項ではなく係数が未知の依存関係で役割を果たします。

両方のクラスでb = a-1とするが、クラス0ではd =（c * 0.99）、クラス1では（c * 0.98）とする

計算結果を表5に示します。流Considerに検討してください。

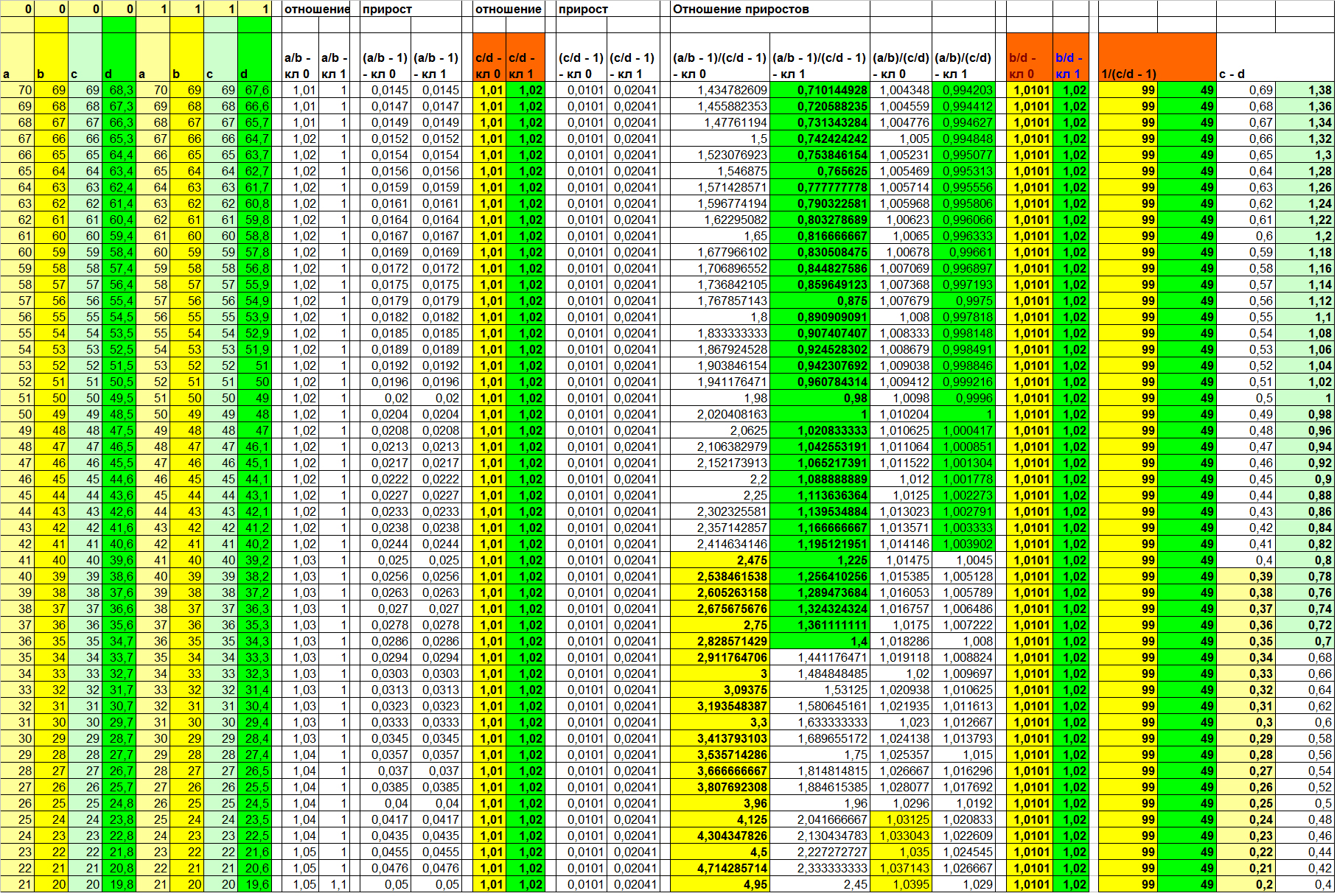
表5

この例での依存性への寄与は係数によってのみ行われるため、予想される100％の分離可能性は、比率関数F（Xi、Xj）= Xi / Xjによって与えられます。また、成長の反対（右側の3列目と4列目）も視覚化を改善します。線形関係の関係も、成長の関係とは異なる結果を示しています。また、さらに悪いことに。

しかし、前の例にあった安定した有益な差分関数（2つの右側の列）は、今回はかなり広い不確実性のゾーンを残しています。そして、それが成長率関数の不確実性のゾーンと一致することは注目に値します。自分を比較します（右側の列1、2、9、10。異なるクラスの互いに素な値が強調表示されています）。

係数と自由項の両方が寄与する場合、状況はどうなりますか？私たちが個々に検討した関係のどれも、サンプルを線形分離可能にしないことが期待されます。ただし、異なる計算列の不確実性の範囲には、サンプルオブジェクトの異なるサブセットが含まれます！もちろん、これは、異なるクラスのオブジェクトを100％分離する一連の計算されたフィーチャに分離超平面を構築する可能性が最も高いことを意味します。

表6のデータの例を見てみましょう。この関数またはその関数は、これらのデータを作成するときに設定した依存関係でどのようにそれ自身を示したかを示します。

クラス0の場合：

B = A - 1 
      

        
        
        
      

     D = 0,95*B - 0,55

クラス1の場合：

B = A - 1,1 
      

        
        
        
      

     D = 0,965*B - 0,5

表6

BとDの関数の計算値については、単純な比率、線形関係の比率、成長、および成長に対する逆数が非常に類似した結果を与えたことがわかります。この場合、前の例（表5）で思い出すように、単純な関係はサンプルを線形分離可能にしましたが、線形関係の関係は非常に広い不確実性のゾーンを残しました（これは、先の例の状況に対する線形関係の関係関数の使用の冗長性によるものです）。

また、前の例とは対照的に、成長の比率は線形関係の比率よりもサンプルを悪化させたことがわかります。そして、差分関数はゲインの比よりもさらに悪いパフォーマンスを与えました（過去のすべての例で、それらの有効性は同じだったことを思い出します）。それは多くを言います。

まず、成長率は単純な違いと同じパフォーマンスを示す必要はありません。

第二に 、異なる関数は、隠れた隠れた依存関係の真の性質に応じて、異なる幅の不確実性のゾーンを残すことができます。

第三に 、目的の隠れた依存関係の真の性質に応じて、異なる関数は異なるクラスのオブジェクトの分離の最良の結果を与えることができます。

他の隠された関係が存在する可能性があり、それらの検索をより適切に整理する方法に進む前に、依存列Dを持つ合成データの別の例を挙げますが、今回は、真の関数D（a、b、c ）表7を見て、もう一度上記の3つの結論が正しいことを確認してください。

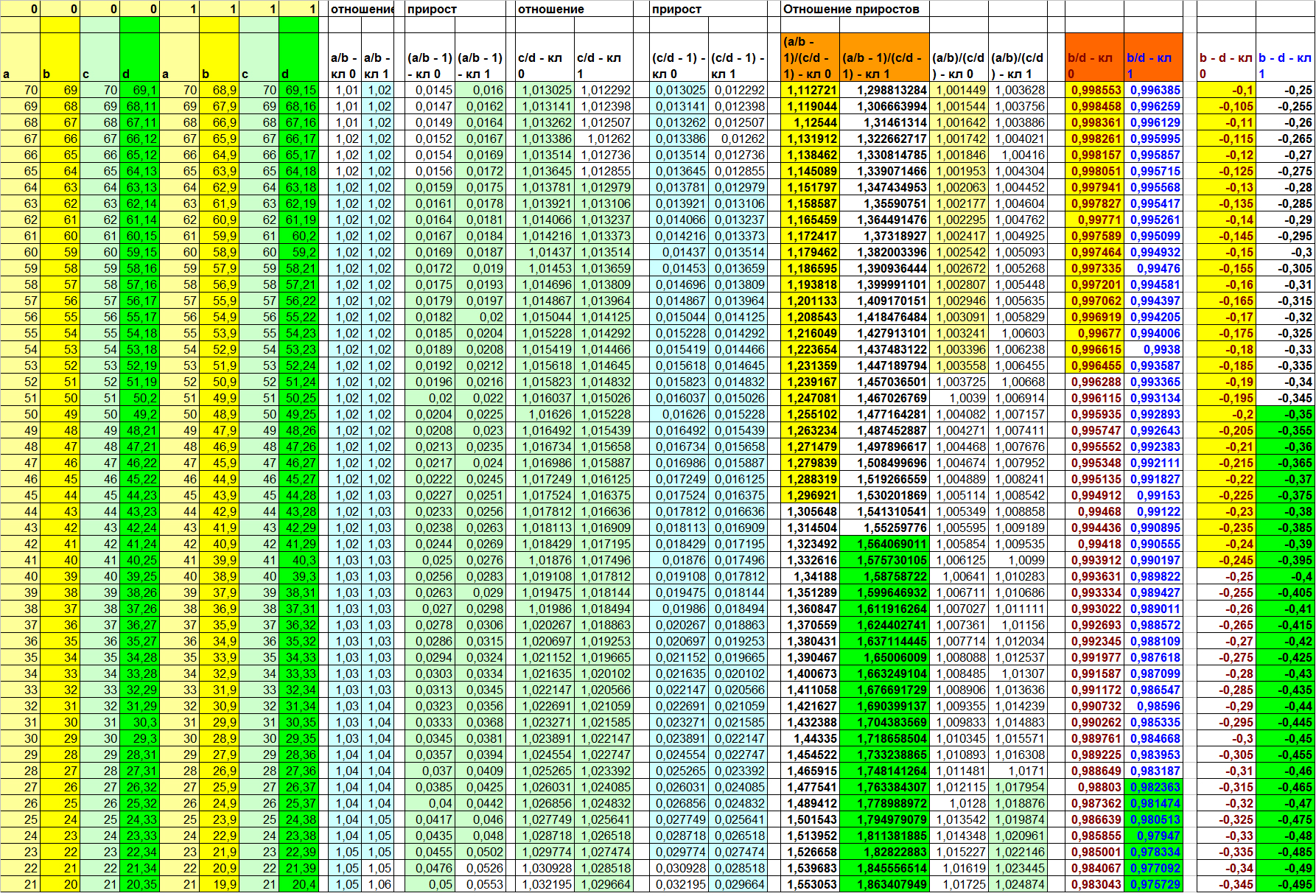
表7

データには、他にどのような依存関係が含まれている可能性がありますか？

上記の例では、フィーチャ間のかなり原始的な線形関係を使用しました。しかし、依存関係が線形関数ではなく、他のより複雑なもので表現されるようにできますか？

なぜだ。たとえば、緑色の微生物のコロニーの繁殖媒体でセンサーによって収集されたデータを想像してください。重要な製品Mの濃度と、照明lxを含む環境の多くの客観的な物理パラメーターが固定されていると仮定すると、依存性M（lx）があると仮定できます。しかし、そのような関係は線形ですか？照明が細菌の繁殖率に線形に影響し、膵臓の濃度がコロニーの数に線形に依存すると仮定すると、依存性は二次関数になるはずです。その理由は、単細胞生殖の方法です。すなわち、細胞分裂。ここでは、単細胞の分裂速度の（速度からの）二次関数的な増加が、時間tの後の数に影響することを証明する必要はないと思います。したがって、たとえば、比率（√M / lx）の計算を試みることができます。これは、露光時の緑色細菌の繁殖率の望ましい線形依存性の近似値と見なされます。そして、2種類の緑色バクテリアの照明速度が再生速度にどの程度影響するかが実際に異なる場合、この新しい機能は確かに最終分類アルゴリズムの品質に役立つ貢献をすることができます。

もちろん、依存関係は非常に異なる可能性があり、基礎は1つまたは別の記号に埋め込まれた意味にあります。ただし、サンプルオブジェクトを記述する機能のセマンティックロードから脱却し、代わりに非表示の依存関係を検索するプロセスを自動化する方法について考えてみましょう。

依存性検索の自動化

そのため、特性記述に非表示の依存関係があるかどうかを判断します。特徴のペアを選択するための複雑なアルゴリズムを探しず、特徴セットN：{X1 ... Xn}全体の接続の存在に関する仮説を単純にテストすることにしたと仮定します。記号のペアから始め、各ペアについて特定の値を計算します。このペアに、セットMから特定の関数を適用した結果：{F1（Xi、Xj）... Fm（Xi、Xj）}。さらに、問題のいくつかの詳細を考慮して、セットの機能がすでに選択されていると考えています。

セットMからm個の関数を適用するペアの数は、n×2の組み合わせの数、つまり次のようになります。

n! / (2! * (n - 2)!) = n * (n - 1) / 2 = (n² - n) / 2 = ½ n² - ½ n

漸近的な複雑さO（n²）を扱っていることがわかります。

そして、これから2つの結論が続きます：

このような網羅的な検索は、事前に計算された特定のしきい値を超えない特徴の数を持つサンプルに対してのみ許可されます。
プライマリデータに基づいて既に計算された列が（成長の比率として）関与する2次依存関係の計算は、そのようなチェックのペアを選択する厳密なアルゴリズムがある場合にのみ許可されます。そうでない場合、完全通過アルゴリズムの複雑度はO（n⁴）になります。一般的なケースでは、二次依存性は何らかの形でベースになっていますが、弱い場合もありますが、非常に有益な一次依存性です。

したがって、上記から次の2つのケースが考えられます。

符号の数はしきい値よりも少ないため、各ペアの仮説をテストする余裕があります。
符号の数がしきい値を超えているため、仮説を完全にテストするペアを選択するための戦略が必要です。

最初に最初のケースを検討します。

兆候の数がしきい値より少ない

厳密に言えば、それ自体で何らかの依存関係を識別することはそれほど重要ではなく、異なるクラスのオブジェクトに対する異なる動作を識別することが重要です。したがって、依存関係の存在を確認する瞬間を省略し、代わりに新しい列の有用性をすぐに確認できます。これを行うには、移動制御で対象の品質メトリックの平均値を測定することにより、この列に既知の高速分類子のいずれかを適用するだけで十分です。そして、関心のある品質メトリックのインジケータが設定したしきい値を超えている場合、新しい列を残すか、品質が必要なレベルに達していない場合は削除します。

もちろん、読者は次のように考えるかもしれません。元の属性に基づいて新しい列が計算され、最終的な分類アルゴリズムにすでに高い有用性がある場合はどうでしょうか。実際、この場合、既存の標識に基づいて追加の標識を作成しただけであることがわかります！純粋な多重共線性！これがまさに、派生フィーチャの分類品質メトリックのしきい値を設定していることです。数個の記号の関数を計算しているため（1つではありません！）、入力で両方の列が非常に有益であったとしても、結果は単なるノイズになります。

これは、各特性の値が特定の平均値と偏差を持つ独立した値である合成データの例によって簡単に検証できます。さらに、異なるクラスの平均には差があり、各クラスのオブジェクトの分布は正常です（たとえば、numpy.random.normalを使用）。したがって、私たちはアプリオリに互いに独立して特性値を生成するため、依存関係を見つける試みはノイズのみにつながり、派生した特性は満足のいく分類品質を与えません。

したがって、上記の例は、派生機能が有益であることが判明した場合、関係の存在を判断できるという事実に賛成しています。

派生フィーチャのしきい値は、さまざまな方法で選択できます。明らかに単純なサンプル全体に対して一度に、または各ペアに対して個別に。 2番目のケースでは、入力に送信された各列の対象となる品質メトリックのインジケーターに応じて、入力しきい値の値を変更できます。

ただし、しきい値を選択するための2番目のオプションの明らかなロジックにもかかわらず、非常に不快な落とし穴があります。要点は、親列の1つで品質メトリックをしきい値として選択することは完全に正しいとは限らないことです。その理由は、品質値がわずかに低い派生属性が実際に新しい依存関係の近似になることがあり、その結果、親とは異なるオブジェクトのセットで誤っている可能性があるためです。そしてこれは、分析のための多くの機能に含まれることで、分類の最終的な品質が根本的に向上することを意味します！

すべての派生フィーチャの共通入力しきい値の選択に関しては、私の意見では、関心のある品質メトリックの値に基づいてしきい値を選択すると非常に便利です（個別に適用する場合！）。したがって、例の精度のために精度を取得する場合、元の列[0.52、0.53、0.53、0.54、0.55、0.57、0.59、0.61、0.63]の値に対して、派生データの最適なしきい値は0の領域にある可能性があります、6（実践が示すように）。何らかの方法で、これはそれほど重要ではありません。なぜなら、パラメーターは学習可能であり、そのトレーニングはアルゴリズムの複雑さを線形的にのみ増加させるからです。何らかの方法でこのパラメータを学習する場合、初期フィーチャの精度の密度分布から開始できます（精度は、この例があるためだけです！）。

原則として、すべてがシンプルです。したがって、2番目のケースに移ります。

標識の数がしきい値を超えています

この条件は、各派生属性のユーティリティを完全に測定する余裕がないことを意味します。またはさらに：記号の各ペアに対して導関数を生成する余裕はありません。それは理解できます：私たちが千の兆候を持っていると想像してください。この場合、組み合わせの数は等しくなり

999 * 1000 / 2 = 499 500

、これにテストされた関数の数が乗算されます！

そして、サーバーが個々の属性に従って選択されたアルゴリズムによって毎秒100回分類品質を計算できる場合でも、属性を生成するアルゴリズムが選択した機能の1つだけで機能するまで、ほぼ1時間半待ちます-仕事は少なくとも奇妙です。一方、多くの自由時間を生成しますが=）

それでは、羊に戻りましょう。この問題はどのように解決できますか？

分類の有用性に基づいて初期特性の数を減らす試みは、最良のアイデアではないかもしれません。なぜなら、記事の最初の部分の合成データの例では、理想的な条件下では、それぞれの親が純粋な形式の完全に不適切な派生属性が明確に示されたためですサンプルを線形分離可能にすることができます。

それではどうする？どうやら、派生的な特徴を計算する必要がありますが、いくつかの制限があります。

まず、ソースフィーチャの数のしきい値をどれだけ超えているかに応じて、ソースサンプルオブジェクトの一部のみに対してそれらを生成して、派生フィーチャの有用性を評価できます。サブサンプルのサイズをどのようにするかという質問には入りません。数学的な統計はこの質問によく答えます。

次に、各派生属性の有用性の評価は、切り捨てられた機能によって実行される必要があります。繰り返しますが、しきい値の超過の程度に応じて、最初のしきい値の数。つまり、その前に、たとえば、導出された特徴の品質を評価するために切り捨てられた学習機能を備えたk個の最近傍の方法を使用した場合、固定パラメーターを使用して使用できます。または、結果のフィーチャセットを重み付けするために、デフォルトのパラメーターを使用してサポートベクターメソッドを実行し、特定の重みを下回る列を破棄します。または、より極端な場合（初期機能の数）には、単純なRosenbaum Q検定などの統計基準の1つを単純に適用できます。残念ながら、この種の基準を適用しても機能を選択することはできませんが、確率密度分布に交互のピークがあるか、異なる方向に単純にバイアスされた中央値があります。

たとえば、クラス1とクラス-1の結果の属性の値をそれぞれ等しくします。または（バイアスされた手段の場合）：明らかに、どちらの場合でも、Rosenbaum基準はサンプルがまったく変わらないと見なします。もちろん、この場合、Pearson基準は完全に機能します。これは、多数の独立した間隔に分割し、各間隔の値の数を個別にカウントする必要があるためです。ただし、同時に、Pearson基準の実行にはより多くの時間が必要になります。これは、最初に大まかな近似で最適化しようとしているパラメーターです。第三に、派生フィーチャの有用性を評価する品質の低下を許容するという事実により、エントリのしきい値もわずかに低くなります。

[9,9,9,9,9,8,8,8,8,8,8,8,8,7,7,7,7,6,6,5,4,3,2,2,1,1,1,1,1,0,0,0,0,0,0,0,0,0] 
      

        
        
        
      

     [9,8,8,7,7,6,6,6,6,6,6,6,6,5,5,5,5,5,5,5,5,5,5,4,4,4,4,4,4,4,3,3,3,3,3,2,2,1,0]

[1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6] VS [1,1,1,1,2,2,2,2,2,3,3,3,3,4,4,4,5,5,6]

したがって、比較的少ない血液で、私たちは印象的な数の最も情報価値のない兆候を取り除きます。しかし、残りのもの（再び、その数に応じて）には、機能の有用性のより良い評価の方法を適用できます。

要約すると、残りのより良い評価のために、最も情報価値のない兆候の最初の迅速な拒絶のための評価の質の低下について話している。

まあ、それはおそらく、完了する時間です。上記のすべてを簡単に要約すると、次の点に注意する価値があります。

結論

多くの場合、分類問題のデータの特性記述の隠れた依存関係F（Xi、Xj）を見つけることができます。これは、独立した記号として機能し、分類の品質を向上させることができます。
, .
, .
k*(n² — n) / 2, k — , n — .
.
ソースフィーチャの数が特定のしきい値を超える場合、派生フィーチャの検証は2つの段階で実行する必要があります。最も有益な派生フィーチャの迅速な拒否と、残りのフィーチャのその後のより良い分析です。仮に、記号の集合M 'から記号F（Xi、Xj）の導関数を計算することができます。これにより、主成分法を元の記号の集合Mに適用できますが、この場合のすべての隠れた依存関係を明示できるかどうかについて疑問が生じます。

まあ、それはすべてこの時間です。そして、はい、レプラコーンが親effectivelyの中で反体制派をより効果的に見つけるのを確かに助けることができます！

機械学習における予測の品質を向上させるための隠れたデータ依存関係の特定