データのジオメトリ2. 2座標および2座標の決定

最初の記事では、要素のメトリックベースを定義します。これは、スカラー積（グラミアン）またはそれらの間の接続（ラプラシアン）の既知の値を持つシンプレックスまたはグラフの頂点のセットです。 ここでは、そのような基準で要素の座標を決定する方法を検討します。

リモート座標

距離座標は、 要素とベンチマークのスカラー積の値-基底の頂点です。 それらを二座標と呼びます。



二座標成分の数は、ベース頂点の数よりも1つ多い $$$l$ および基本空間の次元よりも2単位多い $$$m = l-1$ 。 二座標の例は、距離計量テンソル（DMT）の行（または列）です。



要素のリモート座標は次のように示されます $$$dm$ 、テンソル形式で、基底を示す添字で： $$$dm_a$ 。 座標が属する要素を示す必要がある場合は、角かっこを使用します。 $$$dm（P）$ 。



完全基底には、空間の法線（メジャー）がそれぞれ2座標で含まれ、スカラー単位（要素と法線の積）と要素のスカラー積のセットと基底の頂点を選択できます。 $$$d$ ：



$$$dm = [1; d]$ 。



スカラー積のセット。 $$$d$ マイナーコンポーネントも呼び出します。



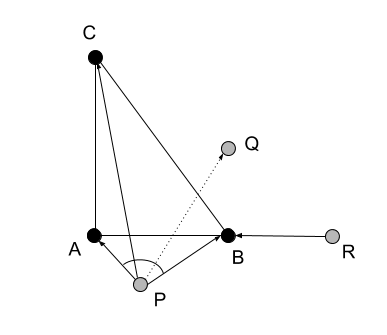
距離座標の値の例を示します。 基本三角形の隣に、三角形の頂点までの距離が既知のP 、 Q 、 Rの 3つのポイントがあるとしましょう（図を参照）。 距離を計算するには、（ XY ）平面上のポイントのデカルト座標を使用します。これは、制御と調整のために与えられます。



ポイントPからポイントA 、 B 、 Cまでの距離のタプルは次のとおりです。 $$$[2、5、26]$ 。 したがって、ポイントの二座標は次のようになります。 $$$dm（P）= [1; -1.0、-2.5、-13.0]$ 。 空間内のすべてのポイントで、2座標のスカラーコンポーネントの値は同じです（このシリーズの記事のフレームワーク内）。



点QとRの 2座標：

$$$dm（Q）= [1; -6.5、-2.0、-6.5]$

$$$dm（R）= [1; -12.5、-2.0、-20.5]$

要素とベクトル

要素の違いによりベクトルが設定されます。 ベクトルの二座標はゼロに等しいスカラー成分を持ちます-この属性によれば、ベクトルは $$$\ vec {PQ}$ アイテムと区別できます。



点とベクトルの座標の記述が異なるジオメトリは、 アフィンと呼ばれます。 このようなジオメトリでは、ベクトルを要素（ポイント）に追加して、新しい要素を取得できます。 ベクトルの場合、加算と減算の演算が定義されます（この場合、スカラー成分の値はゼロのままです）。 しかし、通常、要素を追加する操作には意味がありません。

要素間の距離

ラプラシアン（LMT）が距離座標の計量テンソルであることを示すのは簡単です。 要素Pと要素Qの間の距離の2乗（距離）を決定するには、要素の差のベクトルを見つける必要があります。 $$$\ vec {pq}$ そして、そのレートを計算します 。 ベクトルのノルムは、 双線形形式で決定されます-ベクトルの座標を左右にメトリックテンソルで乗算します。 距離座標の場合、これは次のように記述されます。



$$$q '（P、Q）= || \ vec {PQ} || = dm（P-Q）\ Lm \ dm（P-Q）\ quad（2.1）$



どこで $$$dm（P-Q）= dm（P）-dm（Q）$ -ベクトルの二座標、 $$$Lm$ -ラプラス計量テンソル。



確認します。 目的のベクトルの座標： $$$dm（P-Q）= [1; -6.5、-2.0、-6.5]-[1; -1.0、-2.5、-13.0] = [0; -5.5、0.5、6.5]$ 。 両側のこれらの座標にラプラスメトリックテンソル（LMT）を掛けると、答えが得られます。 $$$q '_ {P、Q} = 13$ 。 デカルト座標の距離から距離の計算を確認できます。 $$$q（P、Q）= 3 ^ 2 + 2 ^ 2 = 13$ 。 答えは一致し、メトリックは機能します。

要素とそのベース空間への投影

からのシンプレックス $$$l$ 頂点が定義します $$$m = l-1$ 次元空間 $$$\ mathbb {R} ^ l$ 。 ベース三角形はベース平面を定義します $$$\ mathbb {R} ^ 2$ 。 要素の二座標の距離成分の数は、空間の次元数よりも1つ多くなります。 これは、2座標により、ベーススペースを超えて属する要素を設定できることを意味します。 $$$\ mathbb {R} ^ n$ 。 この例では、要素はベース三角形の平面だけでなく、その上（下）にも配置できます。



要素の座標は、要素がベース空間のどちら側にあるかを判断することはできません（要素が外側にある場合）。 三角形の例では、三角形の平面の上下にある要素は同じ座標になります。



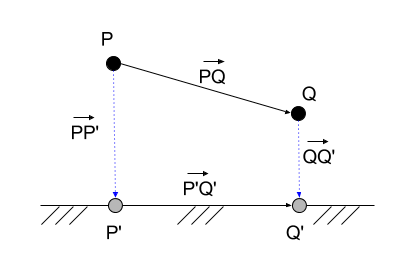
要素がベーススペースに属していない場合、要素の位置を区別する必要があります $$$P$ そしてその宇宙への投影 $$$P '$ 。 要素間の距離の式（2.1）は基本空間でのみ機能します（したがって、距離はダッシュでマークされます）。つまり、要素の投影間の距離の2乗を決定します（要素間の距離ではありません）。



$$$q '（P、Q）= q_a（P'、Q '）\ quad（2.1'）$



ここからインデックス $$$a$ 基礎は、要素間の距離が投影される空間に示されます。 デカルト（および同様の）座標では、それを超える要素の座標を指定する方法はありません。 したがって、デカルト座標系にはそのようなニュアンスはありません。

要素率と基本空間までの距離

式（2.1）の括弧を開くと、「要素の余弦定理」が得られます。 フォームでは、 通常のものと似ていますが、ここでは要素の座標があります（ベクトルではありません）。 したがって、角度や余弦はありません。 しかし、基礎に関連する要素の規範の定義を取得します。



$$$q（P '、Q'）= n（P）+ n（Q）-2 g（P、Q）\ quad（2.2）$



$$$n（P）= dm（P）\ Lm \ dm（P）\ quad（2.3）$



$$$g（P、Q）= dm（P）\ Lm \ dm（Q）\ quad（2.4）$



スカラー $$$n（P）$ 要素のノルムと呼ばれ、スカラー $$$g（P、Q）$ -要素のスカラー積 。 ここで、スカラー積は双線形形式で表されます。



要素のノルムを計算します $$$P$ 図に描かれています。 要素の二座標にメトリックテンソルLMTを2倍すると、ゼロが得られます。 $$$n（P）= 0$ 。 これはどういう意味ですか？



要素のノルムは、ベーススペースに対する相対的な位置を特徴づけます- は、要素からスペースまでの負の距離に等しい ：



$$$n（P）=-q（P、P '）\ quad（2.4.1）$ 。



ノルムの値により、要素が基底の空間に属しているかどうか、そうでない場合はどのくらい離れているかを判断できます。



空間でゼロのノルムポイントを持つ要素を呼び出すと便利です。これらはローカル要素です。 ゼロ以外のノルムを持つ要素は、基底空間に関して非局所的です。

要素のスカラー積

ベクトルのスカラー積の幾何学的な意味はよく知られています-それは方向間の角度の余弦を反映しています。



要素のスカラー積を解釈するには、式（2.2）を使用します（投影図も参照）。 （2.4.1）を考慮して、用語を再分類します。



$$$g（P、Q）=-（q（P '、Q'）+ q（P、P '）+ q（Q、Q'））/ 2 \ quad（2.5）$



2倍のスカラー積は、要素からベーススペースまでの距離と、ベーススペース内の要素の投影間の距離の合計であることがわかります。



で示す $$$g（PP '、QQ'）$ 次の距離の組み合わせ：



$$$g（PP '、QQ'）=-（q（P、Q）+ q（P '、Q'）-q（P、Q '）-q（P'、Q））/ 2 \ quad（2.5 .1）$



この式は、順序付けられたペアのスカラー積です $$$（P、P '）$ そして $$$（Q、Q '）$ 空間への要素の法線。 これで、要素と法線の積との間の距離に関して要素の積を表現できます。



$$$g（P、Q）= -q（P、Q）/ 2-g（PP '、QQ'）\ quad（2.6）$



この式により、基本空間外の要素までの距離を決定できます。



法線のスカラー積がゼロの場合 $$$g（PP '、QQ'）= 0$ （たとえば、要素の1つが基底空間に属している場合）、要素間の距離はそれらのスカラー積によって決定されます。



$$$q（P、Q）= -2 g（P、Q）\ quad（2.6.1）$



式（2.6.1）は、要素のスカラー積の意味を明らかにします-係数（-1/2）を持つ要素間の距離の2乗を反映しています。

ベーススペース外の要素間の距離

要素がベース空間外にある場合、座標に加えて要素間の正確な距離を決定するには、追加情報、つまり空間による法線のスカラー積の値が必要です。 $$$g（PP '、QQ'）$ 。 このスカラー積は、要素が同じスーパースペースに属している場合に計算できます。 この場合、要素の法線間のスカラー積は、単に長さの積です。 次に、非ローカル要素間の距離を計算するための「魔法の」式は次のようになります。



$$$q（P、Q）/（-2）= g（P、Q）+ sign（P、Q）\ sqrt {n（P）\ n（Q）} \ quad（2.7）$



スカラー値 $$$記号（P、Q）$ 要素がスペースの片側にある場合は1、異なる場合は-1。 この式は、アイデンティティ（2.6）の特別な（しかし重要な）ケースです。 適用される多くの問題では、要素の配置は常に片側です。したがって、式（2.7）を使用して、フレーム（地上のレーダー）に対する2座標がわかっている場合、オブジェクト（たとえば、空中にある）間の距離を決定できます。



たとえば、3次元空間にも側面があることを想像するのは簡単ではありませんが、数学にはそうあります。 デカルト座標では、要素が属する辺は、ベースに含まれないn番目のコンポーネントの値の符号によって決定されます。 四面体がデカルト座標x、y、zで指定され、同時に1つのコンポーネントが存在する場合（たとえば、tは時間）、平面t = 0はベース空間を2つの側面に分割すると仮定できます。 コンポーネントt> 0の要素は、ベーススペースの片側にあり、t <0がもう一方の側にあります。

双座標

距離座標に関して相互は、要素の双座標です 。 この用語は、2座標が実際には重心座標の拡張であるという事実に関連しています。 双座標の計量テンソルは距離テンソルです。



要素の双座標はテンソル形式で上付き文字で示されます $$$bm ^ a$ 。 2座標から2座標への（およびその逆の）遷移は、基底の対応するメトリックテンソルを乗算することで実行されます。



$$$bm ^ i = Lm ^ {ij} dm_j、\ quad dm_i = Gm_ {ij} bm ^ j \ quad（2.8）$



三角形の頂点に対する要素Pの双座標を計算します。 LMTと要素の二座標との乗算を実行すると、次のようになります。



$$$bm ^ i = Lm ^ {ij} dm_j = [-3/2; 11 / 12、1 / 3、-1 / 4]$



重心座標の特徴は、コンポーネントの合計が1（この例では、11/12 + 1/3-1/4 = 1）であることです。 各重心成分は、要素座標への基底頂点の寄与（重み）です。 コンポーネントの値が大きいほど、要素はベース頂点に近くなります。

要素軌道

双座標構造は次のように記述できます。 $$$bm = [w; b]$ 。

ここに $$$b$ -重心座標、および $$$w$ -要素の軌道 。 軌道は、要素と基底のオルソセンターのスカラー積を反映します $$$Z$ ：



$$$w（P）= P \ cdot Z \ quad（2.9）$



ジオメトリには、ポイントの次数という概念があります $$$m（P）$ -与えられた球に対する点の相対的な位置。 ポイントから球の中心までの距離の差として定義 $$$q（P、O）$ そして球の半径 $$$r$ ：



$$$m（P、O）= q（P、O）-r（O）\ quad（2.9.1）$







図は、脚の長さの二乗を示しています $$$| PT |$ 三角形 $$$POT$ （点から球に触れるまで）は、点Pの次数の値に等しくなります。 図の点MとNは、次数の有用な特性、つまり値がセグメントの長さの積に等しいことを示しています。 $$$| PM |$ そして $$$| MN |$ 。



要素の軌道は、オルソセンターに対する要素の次数の観点から表現できます。



$$$w（P）= -m（P、Z '）/ 2 =-（r（P）-rs）/ 2 \ quad（2.9.2）$ 。



軌道がゼロより大きい場合-要素は基底のオルソセンター（球）の内側にあり、小さい場合-外側にあります。 重心座標 $$$b$ 基本シンプレックスの空間内の要素の投影の位置を特徴付け、スカラーコンポーネントはオルソセンターに対する空間位置を定義します。



基底の頂点の軌道はゼロです（基底の要素は基底球の表面に属しているため）。 基底の頂点の双座標は、単位座標です（基底成分に単位があり、残りはゼロです-通常、 $$$e$ ） たとえば、三角形の頂点Aの 2座標は[0; 1、0、0]。



要素が基底空間に属していない場合、オルソセンターまでの距離 $$$r（P）$ 要素からその投影までの距離の合計に等しい $$$q（P、P '）$ 投影から中心までの距離 $$$r（P '）$ 。 最初は、反対の符号を持つ要素のノルムに等しくなります。 次に、その投影の軌道を介して要素の軌道を表現できます $$$w_ {P '}$ そして規範 $$$n（P）$ ：



$$$w（P）= w（P '）-n（P）/ 2 \ quad（2.9.3）$



次に、投影軌道は、要素の重心座標と基底のマイナーグラミアンの双線形形式によって決定できます。 $$$G$ ：



$$$w（P '）= -b ^ i（P）G_ {ij} b ^ j（P）/ 2 \ quad（2.9.4）$



第5部では、オルソセンターに対する要素の軌道の概念を、要素の相互軌道の定義に一般化できることを示します。 これは、ベクトルのスカラー積の概念に関連付けられています。

要素とベクトルの双座標

二座標の場合のように、要素の二座標を要素の差のベクトルの二座標から区別する必要があります（アフィンジオメトリ）。 ただし、このシステムの2種類の座標の違いの基準は異なります。 要素の重心成分の合計は1で、ベクトルの成分の合計は0（差があるため）- バランスベクトルになります。 （バランスベクトルは、会計トランザクションで使用されます）。 残りは同様です。 結果はベクトルの空間に残りますが、バイベクトルは加算および減算できます。



ベクトルの軌道（2座標のスカラー成分）は、ベクトルの基底の直交中心の投影を反映しています。 オルソセンターのノルム（球の半径の2乗）には依存しません。



オルソセンターの2座標は、ラプラスメトリックテンソルの境界を形成します。 ラプラシアンの成分の合計がゼロであることを思い出して、ラプラシアン基底の行（列）が特定のベクトルの双座標を反映していると結論付けることができます。 これらは双対基底のベクトルであり、ここでは詳細に説明しません。

距離と2座標のノルム

スカラーコンポーネントは、重心座標にメトリックを追加します。 既知の計量テンソル（DMT）が存在する場合、ベース空間に属する要素間の距離を計算できます。 すべてが標準です-座標差にメトリックテンソルを掛ける双線形形式。 この式は、メトリックテンソルを置き換えた2座標の式に似ています $$$Lm$ に $$$Gm$ と二座標 $$$dm$ 双座標へ $$$bm$ 。 要素差ベクトルの双座標を次のように示す $$$bm（Q-P）= bm（Q）-bm（P）$ 私達は得る：



投影間の距離： $$$q '（P、Q）= bm（Q-P）\ Gm \ bm（Q-P）\ quad（2.10.1）$



アイテムレート： $$$n（P）= bm（P）\ Gm \ bm（P）\ quad（2.10.2）$



スカラー積： $$$g（P、Q）= bm（P）\ Gm \ bm（Q）\ quad（2.10.3）$



要素の双座標とベーススペースに対するそれらの位置を知ることにより、式（2.6）を使用してベーススペース外の要素間の距離を計算することもできます。 そしてこれは素晴らしいです。 一般に、重心座標は要素の相対位置のみを指定すると考えられています。 軌道の形でスカラーコンポーネントを追加すると、要素自体の空間位置だけでなく、ベーススペース外の要素間の距離も決定できることがわかります。

di座標とbi座標を組み合わせる

空間に垂直-特別なベクトル

既に述べたように、基底要素の完全な（主要な）セットには、空間の法線ベクトルが含まれます。 $$$\ mathbf {z}$ 。 法線の二座標は次のとおりです。[0; 1、1、...]。 したがって、法線の双座標は相互に逆になります。[1; 0、0、...]。 法線ベクトルの2座標は、距離計量テンソルの構造に含まれます。



法線がベクトルであるという事実は、二座標のスカラー成分のゼロの値と、重心座標の合計がゼロに等しいという事実によって示されます。



法線のノルム（2座標と2座標の畳み込み）は常にゼロに等しくなります。これは、任意の空間への法線の投影が常に点になるためです。



その結果、空間に法線を要素に追加できます。 このような操作は、要素の標準を変更しますが、空間内での位置は変更しません。 要素の投影の座標を知る $$$P '$ そして規範 $$$n（P）$ 、常に要素自体の座標を決定できます $$$P$ 。 これを行うには、法線ベクトルに要素の半ノルムを乗算し、結果のベクトルを投影座標に追加します。



$$$P = P '+ n（P）/ 2 \ mathbf {z} \ quad（2.11）$

基礎パラメーターと要素の座標との関係

乗算された行列とベクトルの構造が2座標および2座標の関係式（2.8）で明らかにされた場合、座標のスカラー成分とマイナー成分の有用なアイデンティティを取得できます。 双座標の場合：



$$$Lm \ space dm = bm \ space \ Rightarrow \ space \ begin {pmatrix} rs＆s ^ j \\ s ^ i＆L ^ {ij} \ end {pmatrix} \ begin {pmatrix} 1 \\ d_j \ end {pmatrix} = \ begin {pmatrix} rs + s ^ j d_j \\ s ^ i + L ^ {ij} d_j \ end {pmatrix} = \ begin {pmatrix} w \\ b ^ i \ end {pmatrix} \クワッド（2.12）$



ここに $$$d_j、b ^ i$ -要素のマイナーな二および二座標。 このように：



$$$L ^ {ij} d_j = b ^ i-s ^ i \ quad（2.12.1）$



$$$s ^ i d_i = w-rs \ quad（2.12.2）$



式（2.12.1）は、ベクトルに対するラプラシアンの作用の結果が、要素とオルソセンターの差のベクトルとして解釈できることを示しています。

アイデンティティ（2.12.2）（派生では（2.9）および（2.10）も使用されます）は、2座標のマイナーコンポーネントを知って、その程度とオルソセンターまでの距離を取得する方法を示します。



二座標の構造に移りましょう：

$$$Gm \ space bm = dm \ space \ Rightarrow \ space \ begin {pmatrix} 0＆1_j \\ 1_i＆G_ {ij} \ end {pmatrix} \ begin {pmatrix} w \\ b ^ i \ end {pmatrix} = \ begin {pmatrix} 1_j b ^ j \\ w 1_i + G_ {ij} b ^ j \ end {pmatrix} = \ begin {pmatrix} 1 \\ d_i \ end {pmatrix} \ quad（2.13）$



から：

$$$1_j b ^ j = 1 \ quad（2.13.1）$



$$$d_i = w 1_i + G_ {ij} b ^ j \ quad（2.13.2）$



最初の恒等式は、重心成分の合計が1であることを示しています。彼らはそれを既に知っています（しかし、ここでは理由を見ることができます-距離行列の境界として単位ベクトルを使用しているため）

2番目は、距離座標における軌道の役割を示しています。 リモートベクトル $$$d_i$ 基底の頂点の距離ベクトルの加重和で構成されます $$$G_ {ij} b ^ j$ およびベース空間への法線ベクトル。その値は要素の軌道によって決定されます。

ノルムはさまざまなタイプの座標の畳み込みです

両方のタイプ（bi-およびdi-）の座標のスカラー積を使用して、式のメトリックテンソルを取り除くことができます。



投影間の距離： $$q ′（P 、Q ）= b m i（Q - P ）d m i（Q - P ） （2.14.1 ）要素ノルム：$q'(P,Q) = bm^i(Q-P) \ dm_i(Q-P) \quad(2.14.1)$



$$n （P ）= d m i（P ）b m i（P ） （2.14.2 ）スカラー積：$n(P)=dm_i(P) \ bm^i(P) \quad(2.14.2)$



$$$g(P,Q)=dm_i(P) \ bm^i(Q) = dm_i(Q) bm^i(P) \quad(2.14.3)$

すべてをまとめる

主な定義を簡単にリストします。



$$d m i-要素の二座標、要素のスカラー積のセット、および基底のベンチマーク、$dm_i$

$$b m i-要素の双座標、要素のベンチマークに応じた要素の線形展開の係数、座標のタイプの変更（ディックから双方向へ、およびその逆）（「インデックスジャグリング」）は、対応するメトリックテンソルを乗算して実行されます。$bm^i$







$$b m i = d m j L m i j、d m i = b m j G m i j 要素のスカラー積：$bm^i=dm_j Lm^{ij}, \ dm_i=bm^j Gm_{ij}$







$$$g = dm_i Lm^{ij} dm_j = bm^i Gm_{ij} bm^j = bm^i dm_i$



$$→ P Q =Q-Pはベクトル、要素の差、差分ベクトルのノルムは要素の基底空間への投影間の距離です。$\vec{PQ} = Q - P$







$$q （P ′、Q ′）= n （→ P Q）= b m i（Q - P ）d m i（Q - P ）（2.17.3 ） ___がで次の記事、私たちは、順序対の内積を考えます。$q(P',Q') = n(\vec{PQ}) = bm^i(Q-P) dm_i(Q-P) \quad(2.17.3)$