データジオメトリ1.シンプレックスとグラフ

星空は思い出します-ドットは基本的な抽象化であり、周囲の空間の基礎です。

はじめに

これは、（ベクトルではなく）要素に基づいたスペースのベースのプロパティの説明に関するシリーズの最初の記事です。 基底は座標系を定義します-基底に対する要素の位置を特徴付ける一連の数字の形での空間の要素の記述。



空間がメト​​リックである場合、基底は、座標によって空間の要素間の距離を決定できるメトリックテンソルを定義します 。



基底メトリックは、スカラー積の値、または基底の要素間の関係の値のいずれかを使用して指定できます。 したがって、基底は、通常の幾何空間とグラフの二重空間の両方で定義できます 。 幾何空間では、 シンプレックスの頂点が基本要素になります。 グラフには、グラフのノードがあります。

シリーズの概要と内容

最初の記事では、シンプレックスとグラフの相反性を示します。 相互計量テンソルを定義します—基底のグラミアンとラプラシアン。 それらをグラフとシンプレックスのパラメーターに接続します。 空間の法線の役割を示します 。



2番目の方法では、ポイントベースに基づいて座標系を定義します。 2種類の相互座標、つまり2座標と2座標がオブジェクトを特徴づけます。 完全に、座標を使用すると、ベース空間外の要素間の距離を決定できます。



3番目の記事では 、有用な概念-ベクトルのノルムの一般化である順序ペアのスカラー積-空間の要素間の距離の2乗を扱います。



次に、グラフの空間に目を向けます。 ディリクレ問題を解決します。 基本行列の概念が、サブグラフの空間外の要素間の距離の決定にどのように関連付けられるかを示します。



第5部では、基底が変化したときの座標の変換を検討します。 ポイントベースの変換は、たとえば、センサーのローカリゼーション（座標の決定）の問題で使用されます。



最後に、 結論として、最も単純な構造の基礎であるグラフ星を検討します。 これを使用して、 素数の積に分解される正の整数の空間を記述します。



行こう！

リモートマトリックス

n個の要素で構成されるセットがあるとします。 要素は、空間内の幾何学的なポイント、グラフノード、文字、単語、ドキュメント、人物などです。ほとんどすべてのオブジェクトです。 セットの要素の近接度がわかっているとします。 空間内のポイントの場合、近接度はそれらの間の距離の2乗です 。 物理学では、2つのイベント間の近接性の尺度は間隔と呼ばれます 。



距離の2乗の代わりに「クアドランス」という用語が使用されることもありますが、めったに使用されないため、より調和のとれた用語「距離」を使用することが多くなります。 要素間の二乗距離 $$$A$ そして $$$B$ 次のように表示されます。 $$$q（A、B）\ equiv q_ {AB}$ 。 セットの要素間の距離について話している場合、スカラーは行列になります。 $$$Q_ {ab}$ 、小文字のインデックスは複数を示します。 セットの特定の要素から残りまでの距離のタプルは、スカラー距離のセットで構成されます。



$$$q_ {Pa} = [q_ {PA}、q_ {PB}、...] \ quad（1.1）$



それらの間に既知の距離を持つ独立点のセットは、 シンプレックスを定義します。 2次元空間では、シンプレックスは3つの頂点（三角形）、3次元空間では4（四面体）などで定義されます。シンプレックスの次元は、その頂点の数より1少なくなります。 シンプレックスのボリュームがゼロでない場合、頂点は独立しています。



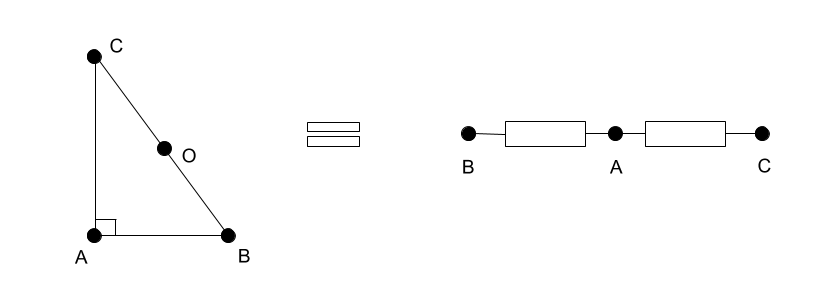
シンプレックスの頂点間の距離は距離行列を定義します $$$Q$ 。 この図は、脚3、4、および斜辺5を持つ直角三角形（2次元シンプレックス）を示しています。その距離行列の形式は次のとおりです。



$$$\ begin {array} {c | c c c} Q＆A＆B＆C \\ \ hline A＆0＆9＆16 \\ B＆9＆0＆25 \\ C＆16＆25＆0 \\ \ end {array}$



電気抵抗回路の場合、距離はネットワークノード間の実効抵抗に等しくなります。 また、電気回路網はグラフであるため、グラフ理論の距離行列は抵抗距離行列と呼ばれます。 したがって、 距離の概念は普遍的です-それは、馴染みのある幾何空間とグラフ空間の両方に使用できます。 また、各非縮退シンプレックスが特定のグラフに対応し、その逆も同様であることを意味します。

マトリックスフレーミング

シンプレックス（またはグラフ）の頂点で、空間の基礎を定義できます。 ただし、 メトリックを指定するには、メトリックテンソルを定義する必要があります。 距離行列は、行列式がシンプレックスのボリューム（この例では、三角形の領域）に関連していないという理由だけで、メトリックテンソルの役割には適していません。



しかし、19世紀に遡って、 A。Cayley（Cayley）は 、距離行列を単位のタプルで境界付けると、結果の行列の行列式がシンプレックスの体積の2乗に比例することを発見しました。 距離行列行列は、Cayley-Menger行列と呼ばれます。



境界操作を定義する $$$エッジ$ 対称行列 $$$M$ モーターカーデ $$$\ mathbf {v}$ およびスカラー $$$c$ ：



$$$エッジ（M、\ mathbf {v}、c）= \ begin {pmatrix} c＆v_j \\ v_i＆M \\ \ end {pmatrix} \ quad（1.2）$



行列 $$$A =エッジ（B、..）$ 行列の境界です $$$B$ それから $$$B$ 部分行列です $$$A$ メイン（角）マイナーと呼ばれます $$$A$ 。

リモートメトリックテンソル（DMT）-基底のグラミアン

数学者（JCGower）は、要素間の距離ではなく、負の半距離で操作する方が便利であることに気付きました $$$-q_ {AB} / 2$ 。

これは、要素間の二乗距離（距離）の公式の開示からわかるように、負の半距離が要素のスカラー積を反映しているためです。



$$$q（A、B）=（A-B）^ 2 = A ^ 2-2 A \ cdot B + B ^ 2$



ここから距離行列の関係を取得します $$$Q$ およびスカラー積行列 $$$G$ ：



$$$G =（\ mathbf {n} \ \ mathbf {1} + \ mathbf {1} \ \ mathbf {n}-Q）/ 2 \ quad（1.3）$



ここに $$$\ mathbf {n} = diag（G）$ -要素のノルム、スカラー積の行列の対角線。 テンソル形式：



$$$G_ {ij} =（n_i 1_j + 1_i n_j-Q_ {ij}）/ 2$



逆数式も同様に重要です-グラミアンに基づいた距離行列を取得できます：



$$$Q_ {ij} = diag（G）_i 1_j + 1_i diag（G）_j-2 G_ {ij} \ quad（1.3.1）$



空間の通常の要素のセットに異常を追加します。 つまり、 空間の法線ベクトル $$$\ mathbf {z}$ 。 通常の空間は、要素の空間に対する直交補数です。 法線と通常の空間の要素のスカラー積は1に等しく、それ自体はゼロです。



$$$\ mathbf {z} \ cdot A = 1、\ quad \ mathbf {z} \ cdot \ mathbf {z} = 0 \ quad（1.4）$



法線は空間のすべてのベクトルに直交しているため、 アナイアレーターとも呼ばれます。 空間の法線を含む要素のセットは、法線がないセットと区別するために、 メジャー （完全）と呼ばれます。 そもそもノーマルがセットに入れられます。



これで、計量テンソルを決定する準備ができました。 リモートメトリックテンソル $$$Gm$ は、主要なセットの要素間のスカラー積のセットです。



$$$Gm =エッジ（G、\ mathbf {1}、0）= \ begin {pmatrix} 0＆1_j \\ 1_i＆G_ {ij} \\ \ end {pmatrix} \ quad（1.5）$



スカラー積（ベクトル）の行列は、 グラム行列と呼ばれます。 要素のスカラー積にも同じ形式を使用します-グラミアン。 したがって、距離計量テンソルは主要な基底のグラミアンです。



3つの頂点のシンプレックス（直角三角形）の場合、距離計量テンソルは次の形式になります。



$$$\ begin {array} {c | cccc} Gm＆*＆A＆B＆C \\ \ hline *＆0＆1＆1＆1 \\ A＆1＆0＆-4.5＆-8 \\ B＆1＆-4.5＆0＆-12.5 \\ C＆1＆-8＆-12.5＆0 \\ \ end {array}$



同じ次元の空間を記述する場合、距離テンソルの次元は通常のベクトルテンソルの次元より2倍大きいことに注意してください。 つまり、このテンソルにはより多くの情報が含まれています。



グラミアンには、下付き文字を使用します。



$$$Gm_ {ij} \ equim Gm$

DMTの幾何学的特性

計量テンソルの行列式 $$$Gm$ シンプレックスのボリュームに関連付けられています $$$vol$ 。 正確な式：



$$$（m！\ vol）^ 2 = -det（Gm）\ quad（1.6）$



どこで $$$m = l-1$ からのシンプレックスによって定義される空間の次元 $$$l$ ピーク。



三角形の面積を計算します。 私たちは持っています $$$m = 2、det（Gm（A、B、C））=-144$ 。 それから $$$2 \ vol = \ sqrt {144} = 12$ どこから $$$vol = 6$ 。 もちろん、この面積は、単に足の長さを掛けることで取得できます $$$vol = 3 \ cdot 4/2$ 。



DMTに含まれる別の有用な特性は、基底の直交中心のノルム値です。 幾何学の観点では、このノルムは、シンプレックスの頂点の周りの記述された球の半径の平方に等しくなります。 つまり、直交中心は次のように解釈できます。 $$$m$ 次元の球。 直交中心は、基底の重要な特性を設定します。 $$$Z$ 。 オルソセンターは標準の空間の要素です $$$rs$ 。 このノルムは、角度のマイナーおよびメジャーグラミアン基底の行列式の比率として見つけることができます。



$$$rs = n（Z）= det（G）/ det（Gm）\ quad（1.7）$



三角形では、基底ノルムは次のようになります。 $$$rs = -900 / -144 = 6.25$ 。

ラプラス計量テンソル（LMT）-ラプラシアン基底

計量テンソルの場合、常に逆数が存在します。これは逆数とも呼ばれます。 計量テンソルの逆は、 ラプラス計量テンソルと呼ばれます $$$Lm$ -LMT。 テンソル関係：



$$$Lm \ cdot Gm = I \ quad（1.8）$ どこで $$$I$ 単位行列です。



なぜ逆距離計量テンソルがラプラスになったのですか？ メインコーナーマイナー（サブマトリックス）はラプラシアンであるため $$$L$ 。 グラフ内のノードと接続を記述する同じマトリックスは、キルヒホッフマトリックスとも呼ばれます。 式（1.8）は、シンプレックスとグラフのプロパティに関連していると言えます。 各ラプラシアンはグラミアンに対応し、逆もまた同様です。 このような相反性により、シンプレックスの幾何学的特性とグラフパラメーターを比較できます 。



ラプラス計量テンソルは上付き文字で示されます： $$$Lm \ equiv Lm ^ {ij}$ 。

LMT構造

ラプラス計量テンソルは、主要なラプラシアンであり、通常の（マイナーな）ラプラシアンの境界です。 境界は、基底のオルソセンターのパラメーターを反映しています（1.7）：



$$$Lm =エッジ（L、\ mathbf {s}、rs）= \ begin {pmatrix} rs＆s ^ j \\ s ^ i＆L ^ {ij} \\ \ end {pmatrix} \ quad（1.9）$



スカラー $$$rs$ オルソセンターのノルム（グラフ、逆幾何学的接続）、 $$$s ^ i = b（Z）$ -オルソセンターの重心座標 。 重心座標は、ベース（参照）（シンプレックスまたはグラフの頂点）に対する要素の重量座標です。 重みの合計は1に等しく、重心成分を正規化するための条件です。

マイナーアイデンティティ

ブロック行列の積の規則に従ってメトリックテンソル（1.8）の乗算を開く、



$$$\ begin {pmatrix} 0＆1_j \\ 1_i＆G_ {ij} \ end {pmatrix} \ cdot \ begin {pmatrix} rs＆s ^ k \\ s ^ j＆L ^ {jk} \ end {pmatrix} = \ begin {pmatrix} 1_j s ^ j＆1_j L ^ {jk} \\ 1_i rs + G_ {ij} s ^ j＆1_i s ^ k + G_ {ij} L ^ {jk} \ end {pmatrix} = \ begin {pmatrix} 1＆0 ^ k \\ 0_i＆I_ {i} ^ {k} \ end {pmatrix} \ quad（1.10）$



4つの基本的なIDを取得します。

オルソセンターの重心座標の成分の合計は1です。



$$$1_j s ^ j = 1 \ quad（1.10.1）$



ラプラシアンの行（および列）の値の合計は0です。これは、ラプラシアンの行がいくつかのベクトルの重心座標であることを意味します。



$$$1_j L ^ {jk} = 0 ^ k \ quad（1.10.2）$ ：



直交中心からのベース頂点（シンプレックスまたはグラフ）の等距離のプロパティ：



$$$G_ {ij} s ^ j = -1_i rs$



最後に、マイナーグラミアンとラプラシアンの関係：



$$$G_ {ij} L ^ {jk} = I_ {i} ^ {k}-1_i s ^ k \ quad（1.10.4）$



行列を表示 $$$I_ {i} ^ {k}-1_i s ^ k$ どこで $$$s$ - 変換行列と呼ばれる特定の重心ベクトル。 たとえば、特定のデータセットの発信元を転送するために使用できます。 $$$X$ 重心座標で定義されたポイントへ $$$s$ 。 これらのマトリックスはプロジェクターです。

ラプラシアン幾何学

シンプレックスの幾何学的パラメーターをラプラシアンの特性と比較してみましょう。

シンプレックスボリュームとラプラシアンポテンシャル

マトリックスツリーの定理は、グラフのスパニングツリーの数をマイナーラプラシアンの行列式に接続します。 以前の記事では、この値はラプラシアンのスカラーポテンシャルと呼ばれていました $$$u$ ：



$$$u（L）= det '（L）=-det（Lm）=-det（Gm）^ {-1} =（m！\ vol）^ {-2} \ quad（1.12）$



ここで $$$det '（L）$ 擬似行列式、つまりラプラシアンのマイナーからの行列式が示されます（ラプラシアン自体は縮退行列であるため）。 $$$m = l-1$ -空間の次元、基底の要素の数より1つ少ない。



グラフのスパニングツリーの数が少ないほど（構造が単純になるほど）、対応するシンプレックスのボリュームが大きくなることがわかります。

ラプラシアン要素

ラプラシアンは、シンプレックスの特性とグラフのノードのパラメーターの両方として考えることができます。 グラフの観点では、ラプラシアンの値はノード間の接続の大きさ（反対符号）であり、対角線上のノードの結合の合計です。



この例のラプラシアンの種類：



$$$L（A、B、C）= {1 \ over 144} \ begin {pmatrix} 25＆-16＆-9 \\ -16＆16＆0 \\ -9＆0＆9 \\ \ end {pmatrix}$



ここでは、ノードAとBの間の導電率（結合重量）は16/144、ノードAとCの間は9/144であり、ノードBとCの間に接続はありません。



次に、ラプラシアンの要素の幾何学的な意味を見つけます。 シンプレックスの各頂点は、対応する反対面に関連付けることができます。 反対とは、指定されたノードに触れないシンプレックスの面を意味します。 明らかに、一般的な場合、そのような顔は多次元です。 三角形では、これは上部の反対側（セグメント）です。 四面体には三角形があります。 与えられた頂点から反対側に垂線を下げると、シンプレックスの頂点の高さが得られます。 頂点の高さの積 $$$h_i$ 反対側の領域に $$$f_i$ シンプレックスの体積を与える $$$vol$ その空間の次元の倍 $$$m$ ：



$$$h_i f_i = m \ vol \ quad（1.13）$



シンプレックスのラプラシアンの要素は、頂点の高さで表現できます。 ラプラシアンの対角要素は、高さに反比例します。



$$$L ^ {ii} = 1 / h_i ^ 2 \クワッド（1.14.1）$



頂点の高さは、基底の残りの頂点の部分空間までの距離です。 つまり、何

シンプレックスの頂点の高さよりも大きい-シンプレックスはコンパクトではありません。 グラフに関しては、頂点の導電率（接続性）が大きいほど、グラフはコンパクトになります。



非対角要素は、シンプレックスの面間の角度の余弦に比例します $$$cos（i、j）$ ：



$$$L ^ {ij} = -cos（i、j）/（h_i h_j）\ quad（1.14.2）$



シンプレックスの面間の直角は、グラフ内の対応するノード間の通信がないことに相当します。



関係（1.12）、（1.13）、および（1.14.1）から、ラプラシアンの痕跡の比の幾何学的意味を得ることができます。 $$$tr（L）$ そのスカラーポテンシャル $$$tr（L）$ 。 この値は、シンプレックスの面の面積の平方の合計に関連付けられています。



$$$tr（L）/ u（L）=（m-1）！^ 2 \ sum {f_i ^ 2} \ quad（1.13.1）$



ここに $$$m-1$ -顔の寸法。

オルソセンターとグラフの接続性

オルソセンター基底のノルムの逆数 $$$rs$ 、幾何学的観点から見ると曲率に等しい。 そして、グラフの空間で、この規範はそのつながりを特徴づけます。 この接続を幾何学的と呼び、 $$$k$ ：



$$$k = 1 / rs \ quad（1.15）$



幾何学的接続の次元は、ノード間の接続の大きさの次元と一致します。 したがって、電気ネットワークの場合、ノード間の導電率がジーメンスで測定される場合、幾何学的接続性はジーメンスになります。





基底のオルソセンターのノルムがグラフの連結性を特徴付ける場合、その重心座標は連結性への寄与として解釈できます。コンポーネントの値は、ノードがグラフにどれだけ接続されているかを示します。グラフの他の部分とのつながりが少ないほど、オルソセンターのこのコンポーネントの値は大きくなります。ジョイントノードには、原則として、接続されたコンポーネントの負の値があります。したがって、オルソセンターの重心座標$$→ s接続ベクトルを呼び出すと便利です。$\vec{s}$

グラフのパラメーター値の例

ウィキペディアで人気のあるグラフのパラメーターを計算します。







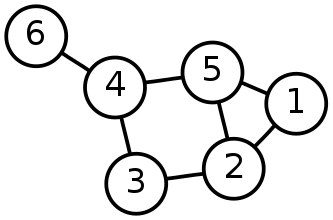
このグラフは、5次元空間の6頂点シンプレックスに相当します。数字の付いた円は、グラフの番号付きノードです。ノード間の接続の強さ（of骨の重量の値）が単位として採用されます。



このグラフの幾何学的接続性は1.663です。これはノードごとの平均接続性です。 6ノードのグラフの最大（7.2）および最小（0.8）接続と比較できます。対称性指数は0.773です。



ノードの連結ベクトル（オルソセンターの重心座標）：[0.364、0.045、0.273、-0.227、0.045、0.500]。ノードの接続が多いほど、その接続の値は低くなり、逆も同様です。4番目のノードの負の接続性に注意してください。これはグラフの唯一のノードであり、削除するとグラフは2つの無関係なコンポーネントに分割されます。負の接続性を持つコンポーネントがグラフの重要なノードである可能性があります。

___

まとめると。主要要素の空間、グラミアン、およびラプラシアンの要素上の相互計量テンソルが定義されています。シンプレックスとグラフの接続が表示されます。次の資料は、ベースの要素の座標を指定する方法を示しています。