ランダムRPGダメージ分布

Dungeons＆Dragonsなどのロールプレイングゲームでは、 ダメージロールを使用して攻撃 ダメージを計算します。 これは、サイコロの転がりに基づいたプロセスのゲームでは論理的です。 多くのコンピューターRPGでは、損傷およびその他の属性（強度、マジックポイント、器用さなど）は、同様のシステムを使用して計算されます。



通常、 random()



呼び出しコードが最初に記述され、次に結果が調整され、ゲームに必要な動作に調整されます。 この記事では、3つのトピックについて説明します。

1. 簡単な調整-平均と分散
2. 非対称性の追加-結果を破棄するか、クリティカルヒットを追加します
3. 乱数を設定する完全な自由、キューブの無限の可能性

基本

この記事では、 0



からrange-1



ランダムな整数を返すrandom( N )



関数があることを前提としています。 Pythonでは、 random.randrange( N )



使用できます。 Javascriptでは、 Math.floor( N * Math.random())



使用できます。 C標準ライブラリにはrand() % N



がありますが、うまく機能しないため、別の乱数ジェネレーターを使用してください。 C ++では、 uniform_int_distribution(0, N -1)



を乱数ジェネレーターオブジェクトに接続できます 。 Javaでは、 new Random()



を使用して乱数ジェネレーターオブジェクトを作成し、そのオブジェクトに対して.nextInt( N )



を呼び出すことができます。 多くの言語の標準ライブラリには、優れた乱数ジェネレーターがありませんが、CやC ++のPCGなど、多くのサードパーティライブラリがあります。



1つのダイから始めましょう。 このヒストグラムは、1つの12面ボーンのロールの結果を示しています： 1+random(12)



。 random(12)



は0から11の数値を返し、1から12の数値が必要なので、1を追加します。損傷はX軸にあり、対応する損傷を受ける頻度はY軸にあります。 1つのボーンの場合、2または12のダメージロールは7のロールと同じくらい可能性があります。







複数のサイコロを振るには、サイコロを使用したゲームで使用されるエントリを使用すると便利です。Nd Sは、 SのサイコロをN回振る必要があることを意味します。 1つの12面のボーンのロールは、両面1d12として書き込まれます。 3d4は、4面ダイスを3回振る必要があることを意味します。 コードでは、これは3 + random(4) + random(4) + random(4)



と書くことができます。



2つの6面ダイス（2d6）を振って、結果をまとめましょう。

 damage = 0 for each 0 ≤ i < 2: damage += 1+random(6)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果は、2（両方の骨に1つ落ちた）から12（両方の骨に6つ落ちた）までの範囲になります。 7になる確率は12よりも高くなります。







骨の数を増やしてもサイズを小さくするとどうなりますか？















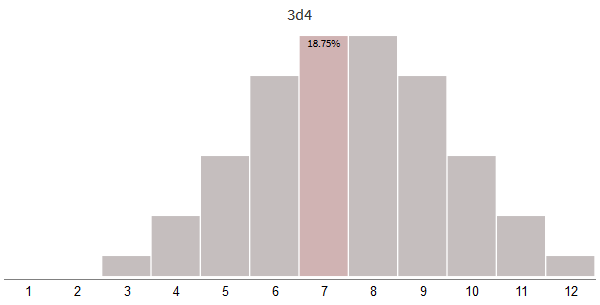
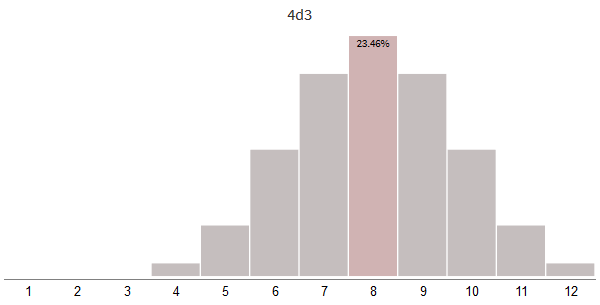
最も重要な効果は、分布が広くなるのではなく、 狭くなることです。 2番目の効果があります-ピークは右にシフトします。 まず、オフセットの使用について調べてみましょう。

一定のオフセット

Dungeons＆Dragonsの武器の一部はボーナスダメージを与えます。 2d6 + 1を記録して、ダメージに対して+1のボーナスを示すことができます。 一部のゲームでは、鎧や盾がダメージを軽減します。 2d6-3と書くことができます。これは、3ポイントのダメージを取り除くことを意味します（この例では、最小ダメージは0であると仮定します）。



ダメージを負（ダメージを減らすため）または正（ダメージボーナスのため）にシフトしてみましょう：



















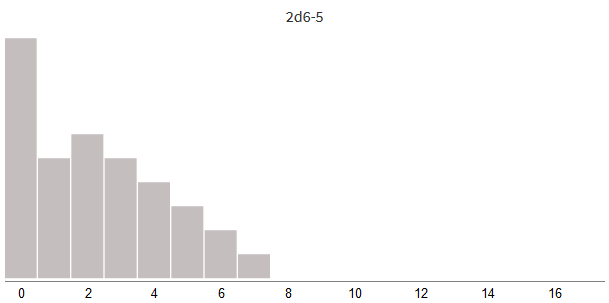
ダメージボーナスを追加するか、ブロックされたダメージを差し引くことにより、単に分布全体を左右にシフトします。

分布の分散

2d6から6d2に渡すと、分布は狭くなり、右にシフトします。 前のセクションで見たように、変位は単純なシフトです。 分布の分散を見てみましょう。



N個の連続したスローrandom( S+1 )



に対して関数を定義し、 0からN * Sの数値を返します。

 function rollDice(N, S): #  N ,       0  S value = 0 for 0 ≤ i < N: value += random(S+1) return value
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

複数のボーンを使用して0から24までの乱数を生成すると、次の結果の分布が得られます。



















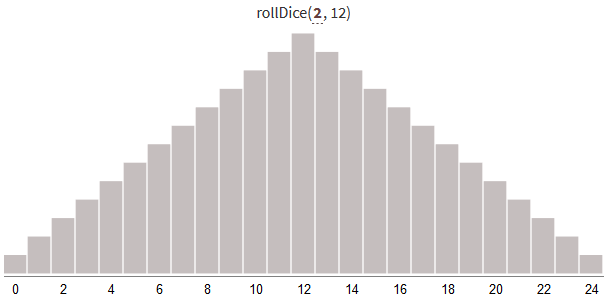
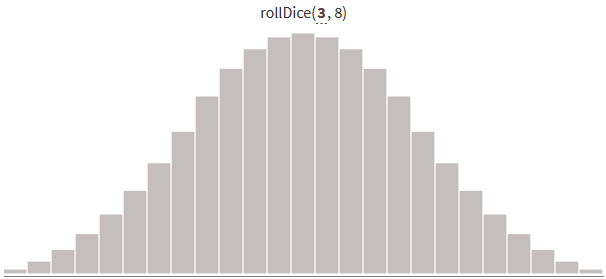
スロー回数を増やし、 0〜N * Sの一定範囲を維持すると、分布は狭くなります （分散が少なくなります）。 より多くの結果は、範囲の中央付近になります。



注： S辺の数が増え（下の画像を参照）、結果をSで割ると、分布は正規に近づきます 。 正規分布からランダムに選択する簡単な方法は、Box-Muller変換です。

非対称性

rollDice( N , S )



の分布rollDice( N , S )



対称です。 平均を下回る値は、平均を上回る値と同じ可能性があります。 これはあなたのゲームに適していますか？ そうでない場合は、非対称を作成するためのさまざまな手法があります。

ショットクリッピングまたはスロー

平均よりも多い値を、平均よりも少ない値よりも頻繁にしたいとします。 このようなスキームは、損傷に使用されることはほとんどありませんが、強度、知性などの属性に適用できます。 それを実装する方法の1つは、いくつかのスローを行い、最良の結果を選択することです。



ロールダイスrollDice(2,20)



2回試し、最大の結果を選択してみましょう。

 roll1 = rollDice(2, 20) roll2 = rollDice(2, 20) damage = max(roll1, roll2)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

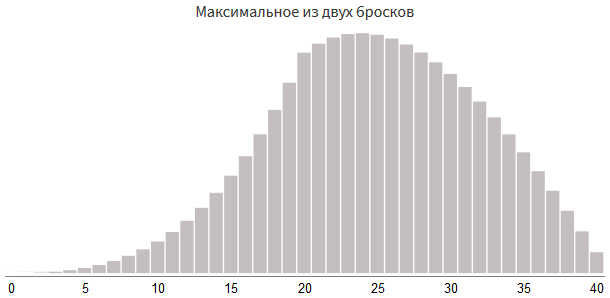
rollDice(2, 12)



とrollDice(2, 12)



rollDice(2, 12)



の最大値を選択すると、 rollDice(2, 12)



の数値が得られますrollDice(1, 12)



数値を取得する別の方法は、 rollDice(1, 12)



3回使用し、3つのうち最適な2つを選択することです結果。 2つのrollDice(2, 12)



いずれかを選択する場合よりも、形状はさらに非対称になります。

 roll1 = rollDice(1, 12) roll2 = rollDice(1, 12) roll3 = rollDice(1, 12) damage = roll1 + roll2 + roll3 #   : damage = damage - min(roll1, roll2, roll3)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

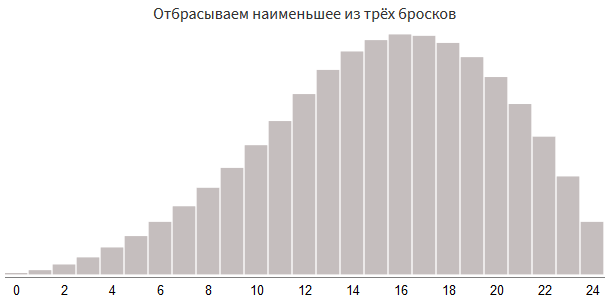
別の方法は、最小の結果をスローすることです。 一般に、これは以前のアプローチと似ていますが、実装がわずかに異なります。

 roll1 = rollDice(1, 8) roll2 = rollDice(1, 8) roll3 = rollDice(1, 8) damage = roll1 + roll2 + roll3 #      : damage = damage - min(roll1, roll2, roll3) + rollDice(1, 8)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これらのアプローチはいずれも逆非対称に使用でき、値の頻度を平均よりも低くします。 また、分布が高い値のランダムバーストを作成すると仮定することもできます。 この分布は損傷のために使用されることが多く、属性にはめったに使用されません。 ここで、 max()



をmin()



ます。

 roll1 = rollDice(2, 12) roll2 = rollDice(2, 12) damage = min(roll1, roll2)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

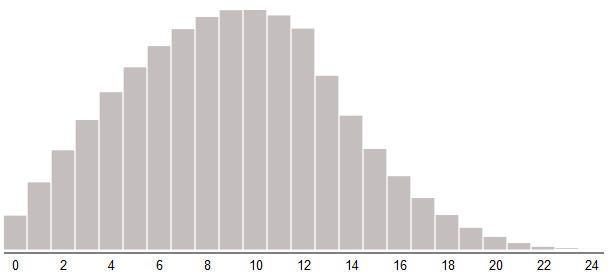
2回の投球のうち最大のものを捨てます

クリティカルヒット

高ダメージのランダムバーストを作成する別の方法は、それらをより直接実装することです。 一部のゲームでは、特定のボーナスが「クリティカルヒット」をもたらします。 最も単純なボーナスは追加のダメージです。 以下のコードでは、5％のケースで重大な損傷が追加されています。

 damage = rollDice(3, 4) if random(100) < 5: damage += rollDice(3, 4)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

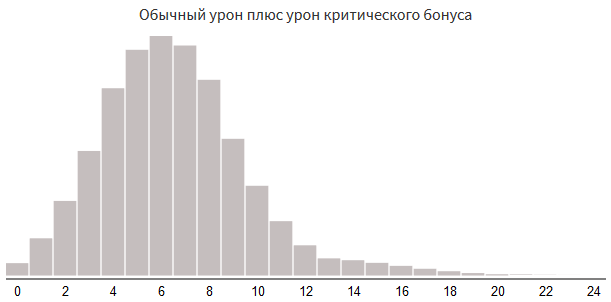
クリティカルヒット率5％





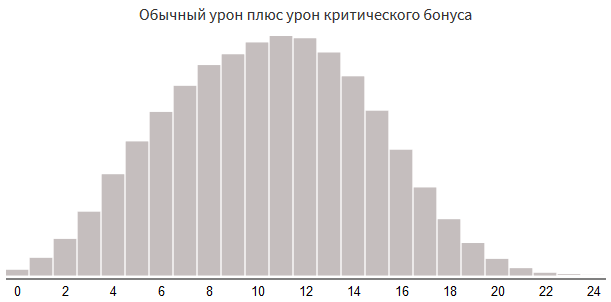
クリティカルヒット率60％



非対称性を追加する他のアプローチでは、追加の攻撃が使用されます。クリティカルヒットでは、追加のクリティカルヒットがトリガーされる可能性があります。 クリティカルヒットが発生すると、2回目の攻撃がトリガーされ、防御を突破します。 クリティカルヒット中、敵は攻撃中にミスします。 しかし、この記事では、複数の攻撃における被害の分布については考慮しません。

独自のディストリビューションを作成してみましょう

ランダム性（損傷、属性など）を使用する場合、ゲームプロセスに必要な分布特性の説明から始める必要があります。

• 間隔：最小値と最大値（ある場合）はどうなりますか？ スケーリングとオフセットを使用して、この間隔の分布に合わせます。
• 分散：値を平均に近づける頻度はどれくらいですか？ 分散を大きくするにはスローを少なくし、分散を小さくするには大きな数を使用します。
• 非対称性：多かれ少なかれ平均値が必要ですか？ 最小、最大、またはクリティカルボーナスを使用して、分布に非対称性を追加します。

以下に、いくつかのオプションの例をいくつか示します。

 value = 0 + rollDice(3, 8) # Min  : value = min(value, 0 + rollDice(3, 8)) # Max  : value = max(value, 0 + rollDice(3, 8)) #  : if random(100) < 15: value += 0 + rollDice(7, 4)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 value = 0 + rollDice(3, 8) # Min  : value = min(value, 0 + rollDice(3, 8))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

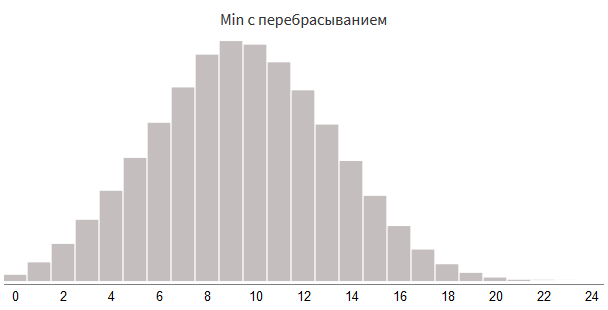
 value = 0 + rollDice(3, 8) # Max  : value = max(value, 0 + rollDice(3, 8)) #  : if random(100) < 15: value += 0 + rollDice(7, 4)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

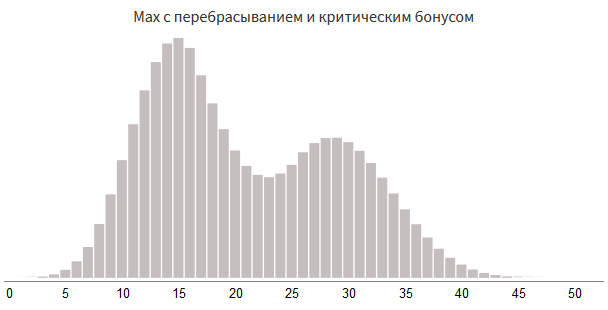
乱数を構造化する方法は他にもたくさんありますが、これらの例がシステムの柔軟性を理解してくれることを願っています。 また、 このダメージロール計算機を見る価値があります 。 ただし、ダイスロールの組み合わせでは不十分な場合があります。

フリーフォーム

入力アルゴリズムから始め、対応する出力分布を調べました。 必要な結果を見つけるために、多くの入力アルゴリズムをソートする必要がありました。 適切なアルゴリズムを取得するためのより直接的な方法はありますか？ はい！



反対に 、ヒストグラムとして表示される必要な出力から始めましょう 。 簡単な例でこれを試してみましょう。



次の割合で3、4、5、6から選択する必要があるとします。







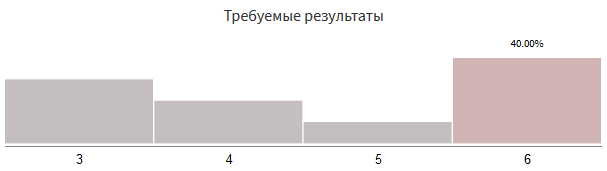
これは、ボーンを投げることで取得できるものには対応していません。



これらの結果のコードを書く方法は？

 x = random(30+20+10+40) if x < 30: value = 3 else if x < 30+20: value = 4 else if x < 30+20+10: value = 5 else: value = 6
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次のステップに進む前に、このコードを調べて、どのように機能するかを確認してください。 さまざまな確率表に使用できるように、コードをより一般的にしましょう。 最初のステップは、テーブルを作成することです：

 damage_table = [ #  (, ) (30, 3), (20, 4), (10, 5), (40, 6), ];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この手書きのコードでは、各if



構造はx



を確率の合計と比較します。 手動で定義された合計を使用してif



構造を個別に記述する代わりに、すべてのテーブルエントリを循環できます。

 cumulative_weight = 0 for (weight, result) in table: cumulative_weight += weight if x < cumulative_weight: value = result break
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に一般化するのは、テーブルエントリの合計です。 合計を計算し、それを使用してランダムなxを選択しましょう。

 sum_of_weights = 0 for (weight, value) in table: sum_of_weights += weight x = random(sum_of_weights)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すべてを組み合わせて、テーブル内の結果を検索する関数とランダムな結果を選択する関数を作成できます（これらを損傷テーブルクラスのメソッドに変換できます）。

 function lookup_value(table, x): # ,  0 ≤ x < sum_of_weights cumulative_weight = 0 for (weight, value) in table: cumulative_weight += weight if x < cumulative_weight: return value function roll(table): sum_of_weights = 0 for (weight, value) in table: sum_of_weights += weight x = random(sum_of_weights) return lookup_value(damage_table, x)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

テーブルから数値を生成するコードは非常に簡単です。 私のタスクでは十分に高速でしたが、プロファイラーがそれが遅すぎると報告した場合、バイナリ/補間検索、ルックアップテーブル、またはエイリアスメソッドを使用して線形検索を高速化してみてください。 逆変換法も参照してください。

独自の分布を描く

この方法は、 任意のフォームを使用できるという点で便利です。

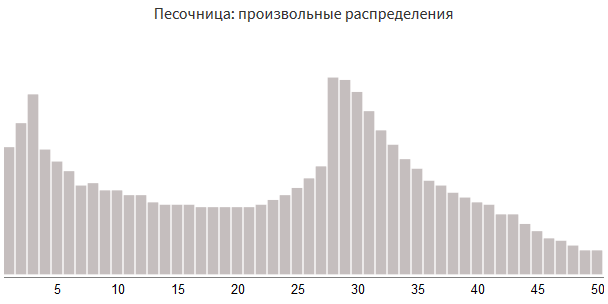
 damage_table = [(53,1), (63,2), (75,3), (52,4), (47,5), (43,6), (37,7), (38,8), (35,9), (35,10), (33,11), (33,12), (30,13), (29,14), (29,15), (29,16), (28,17), (28,18), (28,19), (28,20), (28,21), (29,22), (31,23), (33,24), (36,25), (40,26), (45,27), (82,28), (81,29), (76,30), (68,31), (60,32), (54,33), (48,34), (44,35), (39,36), (37,37), (34,38), (32,39), (30,40), (29,41), (25,42), (25,43), (21,44), (18,45), (15,46), (14,47), (12,48), (10,49), (10,50)]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアプローチでは、サイコロのロールによって作成された分布に限らず、あらゆるゲームプレイに一致する分布を選択できます。

おわりに

ランダムなダメージスローとランダムな属性は簡単に実装されます。 あなたは、ゲームデザイナーとして、最終的なディストリビューションが持つプロパティを選択する必要があります。 サイコロを使用する場合：

• スローの数を使用して分散を制御します。 少量は高分散に対応し、逆も同様です。
• スケールを制御するには、ボーンの オフセットとサイズを使用します。 乱数をXからYの範囲にする場合は、 N回のスローごとに、0から（YX）/ Nの乱数を取得する必要があります。その後、 Xが追加されます。 正のオフセットは、ダメージボーナスまたは属性ボーナスに使用できます。 負のオフセットは、損傷を防ぐために使用できます。
• より頻繁に値が平均より大きいか小さい場合は、 asymmetryを使用します。 属性のスローは、多くの場合、スローに対して平均値よりも高い値を必要とします;それらは、最大値、3つのうちの最高値、または最小値をスローすることで取得できます。 ダメージロールは通常、平均値よりも低い値を必要としますが、最小またはクリティカルボーナスを選択することで取得できます。 敵とのランダムな遭遇の複雑さのために、平均以下の値もしばしば使用されます。

ゲーム内での分布の違いを考えてください。 攻撃ボーナス、ダメージブロック、クリティカルヒットを使用して、単純なパラメーターで分布を変えることができます。 これらのパラメーターは、ゲーム内のアイテムに関連付けることができます。 元の記事のサンドボックスを使用して、これらのパラメーターが分布に与える影響を観察します。 プレイヤーのレベルが上がったときの配布の仕組みを考えてください。 AnyDiceを使用して分布を計算する際の時間の経過に伴う分散の増減に関する情報については、 このページを参照してください （これについては素晴らしいブログです ）。



サイコロのあるボードゲームプレーヤーとは異なり、乱数の合計に基づく分布に限定されません。 「独自のディストリビューションを作成してみましょう」セクションで記述されたコードを使用すると、任意のディストリビューションを使用できます 。 ヒストグラムを描画し、データをテーブルに保存し、この分布に基づいて乱数を描画できる視覚的なツールを作成できます。 JSONまたはXML形式のテーブルを変更できます。 Excelでテーブルを編集して、CSVにエクスポートすることもできます。 パラメーターなしの割り当てにより柔軟性が向上し、コードの代わりにデータテーブルを使用すると、コードを再コンパイルせずに高速の反復が可能になります。



単純なコードに基づいて興味深い確率分布を実装する方法は多数あります。 まず、必要なプロパティを決定してから、それらのコードを選択します。