コンピューターゲームのジオメトリ

みなさんこんにちは！ むかしむかし、私は簡単なフラッシュのおもちゃを作りました。 例：おもちゃ-壁に触れず、移動するオブジェクトを避けずに、マウスカーソルを迷路内で移動します。 これらのオブジェクトの一部は、事前に設定されたパスに沿って移動し、カーソルを追跡し、他の移動オブジェクトでカーソルを撃ちます。



今私はアンドロイドのプログラミングに興味を持ち、同じおもちゃを作りました。 そして、彼はそのとき出会ったのと同じ幾何学的問題に直面しました。







タスク1：壁を描きます。 タスク2がすぐに発生します：ポイントが壁に触れるかどうかを判断します（ゲームを失うか、続行します）。



これを行うために、壁を長方形と多角形の形状に分割しました。



長方形を使用すると、すべてが簡単です。描画するだけです：

canvas.drawRect(x1, y1, x2, y2, paint);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ポイントがその中にあるかどうかを確認します。

 public boolean isTouched(float x, float y){ return (x>x1)&&(x<x2)&&(y>y1)&&(y<y2); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ポリゴンの状況はそれほど単純ではありません。それを描くのはもう少し難しいです。

 Path path = new Path(); paint.setStyle(Paint.Style.FILL); path.moveTo(x1, y1); path.lineTo(x2, y2); path.lineTo(x3, y3); ..... path.lineTo(x1, y1); //  path.close(); canvas.drawPath(path, paint);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、ポイントとのタッチを確認することはさらに困難です。 私は学校の幾何学コースを思い出そうとし、それをグーグルで調べてこの解決策を見つけました：



多角形は凸型でなければなりません。







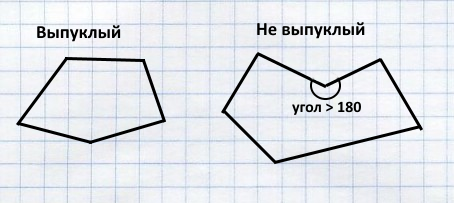
そして、時計回りに記述する必要があります。







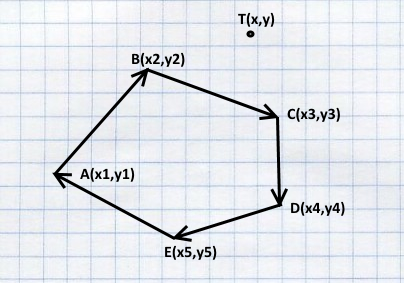
さらに、各エッジには初期および最終座標があります。つまり、実際にはベクトルです。 また、ポイントがその右か左かを判断できます。



これには簡単な式があります。

 private boolean isLeftHandSituated(float dotX, float dotY, float x1, float y1, float x2, float y2){ float d = (dotX - x1) * (y2 - y1) - (dotY - y1) * (x2 - x1); return d>0; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ポイントが内側か外側かを判断するために、すべてのエッジを巡回し、少なくとも1つのエッジがポイント（この場合はエッジBC）にある場合、多面体は時計回りに記述されているため、外側にあります。



タスク3：黄色の絵文字。 ポイントが特定の距離で彼に近づくと、彼はポイントを追いかけます。 この特定の距離は、ピタゴラスの定理を使用して計算できます。

 float dx = dotX - smileX; float dy = dotY - smileY; double distance = Math.sqrt((dx * dx + dy * dy));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ドットを追いかけてスマイリー。 これはどういう意味ですか？ これは、特定の時間間隔（次のフレーム）ごとに、座標が特定の距離だけポイントに近づくことを意味します。 このフレームあたりの距離は基本的に速度です。 可変速度に名前を付けました。







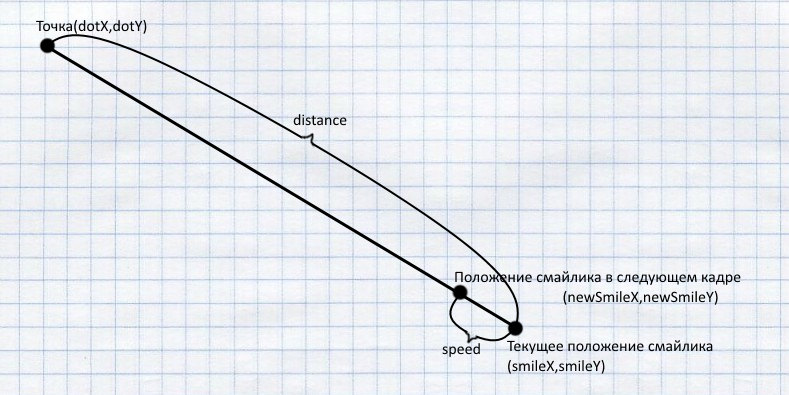
次のフレームの絵文字の座標は、次のように計算できます。

 private float speed=5; double rate = speed / distance; newSmileX = smileX + (float) (dx * rate); newSmileY = smileY + (float) (dy * rate);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

タスク4：大砲は常にポイントに向けられます。 回転する角度を計算する方法は？ とても簡単です。 これにはatan2メソッドがあります。

 float dx = dotX - cannonX; float dy = dotY - cannonY; double theta = Math.atan2(dx, dy); //    angle = Math.toDegrees(theta); //   .
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結論：この記事はかなり簡潔で短いものであることが判明しましたが、多くの初心者のゲーム開発者にとって役立つことを願っています。 トレーニングと開発の皆さんに幸運を！