「マインスイーパ」の不快な状況
この地位では、私の周りに多くの地雷が存在することを知っていますが、それらがどこにあるかを判断することはできません。 いくつかの地雷は2つの場所(ピンクまたはブルー)のいずれかにあり、地雷のグループは2つの組み合わせ(ライト/ダークグリーン)のいずれかにあります。 さらに、左上隅に「5」と「6」という困難な状況がまだありますが、それは決して強調しませんでした。

ブルー/ピンク-相互に排他的なペア、ライト/ダークグリーン-相互に排他的なグループ
掃海艇:論理または確率
マインスイーパは2つの方法でプレイできます:論理的ゲームまたは確率的ゲームとして。
技術的には、確率は論理を意味します。 鉱山が特定の場所にあることを論理的に証明できる場合、確率は100%です。 彼女がこの場所にいないことを証明できる場合、確率は0%です。 つまり、ある意味では、確率だけが重要です。 ただし、プレーヤーは論理的な演usesを使用して、このような絶対的な状況を認識します。 時々、特に難易度の低いレベルでは、レベルを渡すだけで十分であり、確率の計算は必要ありません。
しかし、世界の論理全体があなたを救うことができない状況があります。 簡単な例は、下部中央に表示される「T」の状況です。 追加の隣接する鉱山によって少し複雑になります。 (最も単純な場合、「2」は「1」に、「5」は「3」に置き換えられるため、状況は対称的です。)
これらのセルの1つに残っている1つの地雷の推定位置に関する詳細情報を取得する方法はありません 。 チャンスは50 x 50です-コインを投げることができます。 このようなものを入手したら、すぐに選択して、後回しにすることは避けてください。 推測が間違っている場合、少なくともフィールドの残りの部分を解決する時間を節約できます。 (しかし、個人的には完全を目指して努力しているので、そのようなケースは後回しにします。推測しないことで自分を責めないでください。勝ち負けがコイン投げに依存する場合-これは悪いゲーム設計です。)
ゲーム終了時の戦術
エンドゲームでは、非常に単純な戦術を使用できます-残りの地雷の数を数えます。 フィールドの右下を除くすべてを決定したとします。 データに対応する鉱山の構成は2つしかありません。

右下隅の可能な鉱山構成
そのような位置があり、カウンターが2つの地雷しか残っていないことを示す場合、答えは準備ができています:これは構成Bであるはずです
カウンターに3つの地雷が残っていると表示されている場合、これは必ずしも構成Aではありません。 これは、残りの鉱山が3x3セルの右下グループの1つにあるスキームBです。
実際、オッズは構成Bに有利です。
局所確率
「ローカル」でのみ確率を調べると、マークされた相互に排他的なグループの各セルには、50〜50の確率で地雷になることがわかります。 「ローカル」と言えば、2つの未知のセルの隣に「1」がある場合、それらのそれぞれの隠れた地雷の確率は50%です。
下部中央で発生したのはこの状況です。未知のペアに隣接する各隣接セルには1つの鉱山が含まれています。つまり、各隣接データフラグメントは50%の確率を想定しています。 左上隅の同様の状況:
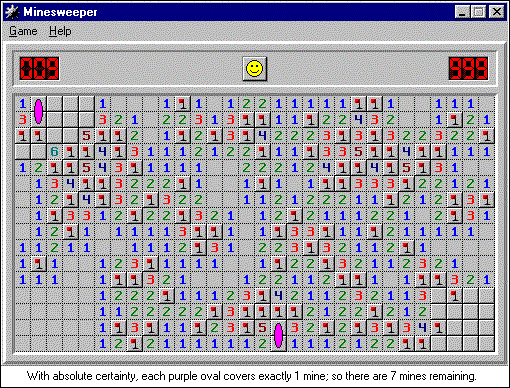
絶対精度では、ピンクの楕円のそれぞれに1つの鉱山があります。つまり、残り7分です。
右下の状況も多少似ています。「境界」の各数字の隣には、1つの鉱山と2つのセルがあります。
セルの隣に1つの隠れた地雷があり、3つの閉じたセルがある場合、各セルに地雷が存在する確率は33%です。 4つの閉じたセルのそれぞれに25%の確率があります。 2つの隠れた地雷と3つの閉じたセルがある場合、各セルの確率は66%です。
以下は、フィールド全体の「ローカル確率」状況です。
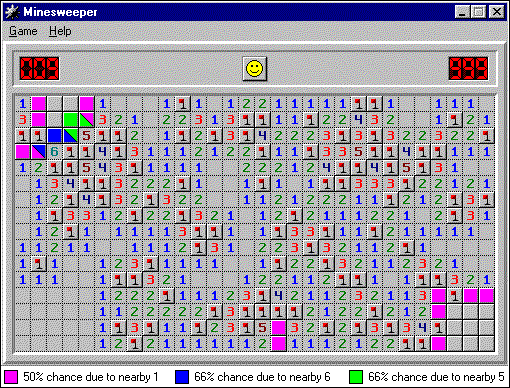
ご覧のとおり、左上の領域のいくつかのセルにはいくつかの確率があります。 「2」と「6」の隣の閉じたセルと「3」と「5」の隣の閉じたセル。 (それらのおかげで「5」と「6」の隣のセルはまだ66%の確率を持っているので、目に見える矛盾はありません。)
ローカル紛争解決
おそらく、競合するローカル確率の存在が何を意味するのか疑問に思うでしょう。 直感は、勝つ可能性が最も高いことを示唆する場合があります。 たとえば、「6」と「2」の間のセルには実際に66%が必要です。 これは、確率50%の左端のセルでは、実際には33%に等しいことを意味します。 または、何らかの方法で優先順位を組み合わせることもできます。おそらく、確率は5/6または平均値になります。
しかし、これは実際には真実ではありません。 確率の導出元のデータは互いに独立しているわけではないため、簡単な数学的計算は正しくありません。 中央で約50%ダウンしているとローカルで推測される理由は、それが他の何ものからも本当に独立しているからです。 すでに利用可能なデータに従ってフィールドをランダムに再作成すると、モデルのちょうど半分で、鉱山は2つのセルのいずれかになります。 (確率は、確率を計算するためのルールが特定の状況に適用可能であるかを判断できない人々を混乱させることがあります。現在の状況では、これらはすべて同等に考えられます)
つまり、左上隅の状況で正しい測定を行うには、既に収集されたデータを満たす可能性のあるすべての地雷構成を検討し、それらの何パーセントが目的の位置に地雷が含まれているかを計算する必要があります。
直接カウントには時間がかかります。 幸いなことに、他の方法があります。
カウント構成
確率を計算する抽象的な方法は、すべての可能な地雷構成をバイパスし、収集されたデータを満たさない構成を破棄し、各可能な位置の統計を計算することです。
より実用的なアプローチは、破棄できないオプションのみを考慮することです。 これを行うには、ロジックを適用し、利用可能なデータに対応する可能性のあるすべての状況を生成する必要があります。 右下隅にはすでに2つのオプションを示しましたが、左上隅の確率は次のとおりです。
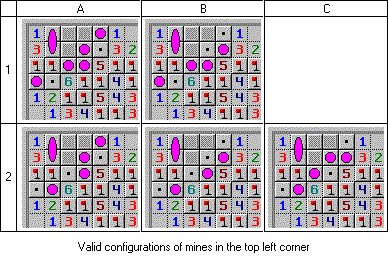
左上隅の可能な構成
(前述のように、2つのセルの高さを持つ楕円形は、鉱山がどのセルにも等しく存在する可能性があることを示しています。これら2つのケースを個別にリストできます。つまり、10の構成が判明しますが、私たちには役に立ちませんテーブルの構造:2行(「1」と「2」として番号が付けられています)は、4行目の地雷の位置が異なります。3列は、2行目の地雷の位置によって特徴付けられます。)
今、叫ぶ誘惑があります:「ええ、ここには5つのケースがあります。それで、鉱山の可能な位置のそれぞれについてケースの数を計算できます。」 たとえば、地雷は4番目の行(左下「1」の隣)にあり、2つの上部ケースでは左側に、3つの下部ケースでは右側にあります。 したがって、「6」の次に右側にある確率は60%であると判断できます。 (これは、競合するローカル確率が50%と66%のポジションです。)
ただし、微妙な点が1つあります。地雷の数は場合によって異なります。A1では 6分、 B2では4、その他の場合は5です。
見つからない鉱山のカウント
この微妙さの詳細な研究のために、右下のより単純な状況に戻りましょう。

右下隅の可能な構成
すでにフィールドの残りの部分を開いており、残り3つの鉱山があることを知っているとします。
ちょうど3つの鉱山がある構成Aが最も可能性が高いことを示唆するのは魅力的です。 しかし、これは真実ではありません。
もう1つの誘惑は、鉱山の数とセルの数を覚えて、「下の3x3領域が空になる可能性はどれくらいか」と言うことです。 これも事実ではありません。 これが間違いである理由を説明するのは非常に困難です。おそらく、 モンティホールのパラドックスと比較することができます。 ただし、実際にはこの状況でのチャンスは地雷の総数とフィールドのサイズに依存しないと言えば十分です。
正しい答えは次のとおりです。3つの地雷の可能な構成はどれくらいあるのでしょうか。 図から、2つの構成AとBがあることがわかります。 しかし、 Bには 2つの鉱山しかありません。 3番目の鉱山は、まだデータを収集していない3x3下部のセルのいずれかに配置できます。 つまり、 Bには合計9つの構成オプションがありますが、私はそれらをすべて描写しませんでした。
したがって、可能な構成は10個のみです。 10の構成のそれぞれも同様に可能性があります。 (前述したように、これは確率を理解するために重要です。コンピューターがこれらのオプションのいずれかを生成する可能性は小さいですが、コンピューターは(わかっている限り) すべての構成に平等な機会を与えたため、等しく小さいです。 10個の「ワシ」が一列に並んでおり、 2個の「ワシ」、1個の「尾」、1個の「ワシ」、3個の「尾」、1個の「ワシ」、1個の「尾」、1個の「ワシ」のシーケンス。 「ワシ」と「5つの尾」、ただし「ワシ」と「 「マインスイーパでは、コイントスシーケンスに類似した地雷構成を扱っています 。)
10個の構成( Bが 9個、 Aが 1個)のそれぞれが等しく発生する可能性があるため、この場合の構成Bの確率は90%です!
この段階で4つの鉱山がある場合、構成Aには9つのオプションがあります。 構成Bには、左下隅の2つの地雷の配置ごとに1つのオプションがあります。 これはC (9.2) 、つまり9!/((9-2)!* 2!)または9 * 8 / 2、36に等しいです。この場合、構成Bの確率は75%だけです。
5つの鉱山では、構成Aには36のオプションがあり、構成Bには 9 * 8 * 7/6 = 84のオプションがあります。 つまり、 Bのオッズは66%強です。
6分の場合、 Bは60%の確率になります。 7つの地雷がある場合、 Bは50%しかありません。 8つの地雷がある場合、 BはAよりも少なくなります。 この場合、構成の残りの位置に非常に多くの地雷があるため、少なくなります。 11分が残っている最悪のシナリオを考えてみましょう。 (この可能性は非常に小さいですが、そのような状況が発生した場合、これらの確率が適用されます。)構成Bでは、すべての閉じたセルに、1つを除くすべての構成Aに地雷があります。 つまり、 Aには9つのオプションがあり、Bには1つのオプションしかありません。
最終決定
既存のフィールドでは、残り9分です。 そのうちの1つは中央下部にあり、その位置は完全に独立しているため、無視できます。 つまり、この場合を除き、フィールド全体を検討します。8分しか見つかりませんでした。 (混乱を避けるため、左上隅の楕円を明示的にカウントし続けます。これは左上隅の画像であるためです。)
そのうちの1つ(A1 + A)を除き、左上の構成と右下の構成の任意の組み合わせが形成される場合があり、これには9分かかります。 したがって、これらの可能な構成のそれぞれをリストし、残りの地雷と独立セルをカウントする必要があります。
実際、クローズドセルの数は独立しています。右下隅に9個、左上隅に3個、つまり12個しかありません。
| 左上 | 右下 | 鉱山の数 | 残り最小 | クローズドオプション |
|---|---|---|---|---|
| A1 | B | 8 | 0 | 1 |
| B1 | A | 8 | 0 | 1 |
| B1 | B | 7 | 1 | 12 |
| A2 | A | 8 | 0 | 1 |
| A2 | B | 7 | 1 | 12 |
| B2 | A | 7 | 1 | 12 |
| B2 | B | 6 | 2 | 66 |
| C2 | A | 8 | 0 | 1 |
| C2 | B | 7 | 1 | 12 |
したがって、合計118の可能な組み合わせがあります。 これに基づいて、左上および右下の各構成の組み合わせの数を個別に計算できます。
| 構成 | オプション | 割合 |
|---|---|---|
| A1 | 1 | 1 |
| B1 | 13 | 11 |
| A2 | 13 | 11 |
| B2 | 78 | 66 |
| C2 | 13 | 11 |
| A | 15 | 13 |
| B | 103 | 87 |
次に、フィールド上の各セルを調べて、出現する確率の数を合計し、118で割ってその確率を計算しました(実際、上記の割合を合計するだけです)。さらに、平均して、閉じたセルのそれぞれに地雷があります118のオプションのうち15(つまり、少なくとも1つのクローズドセルに地雷がある可能性が非常に高い)。 [これは、残りの地雷の数にクローズドオプションを掛けることで計算できます。これにより、クローズドセルの地雷の平均数が得られます。]

地雷の確率
(これは利用可能なすべての情報を表示するわけではありません。たとえば、87%の2つの濃い緑色のセルの確率は関連していることを知っています。 Aも接続されています。残りの青の13パーセントのセルは接続されていません。そのうちの1つに地雷がある場合、残りのセルに地雷がある可能性は低くなります。
ゲームをプレイする
おそらく、マインスイーパをプレイするとき、これらすべての計算に目を通す必要はないでしょう。
私も。
しかし、 実際にはすべての可能な構成を左上隅と右下隅にリストしました。 1つの構成( B2-B )で、1分が他のすべての構成よりも使用されていないことに気付き、「最小分はより多くのクローズオプションを意味します」というタイムテスト済みのルールを適用しました(クローズセルの数が数の2地雷が見つかりません)。 これは、鉱山の数が少ない構成の可能性がはるかに高いことを意味します。
左上隅に多くの構成があったため、セルのオッズを決定することは非常に困難です。 したがって、右下隅の構成Bの方がはるかに可能性が高いことがわかり、誤って適切なセルの1つを選択しました。 (右下隅を終了し、残りの地雷の数に関する詳細情報を入手して、左上隅を完了することができることを望んでいました。その後、選択のためにコインを中央下にドロップする必要があります。もちろん、選択する必要がありました有用な情報を取得する可能性を最大化するセルですが、これらの推測により、右下隅からさらにデータを収集できるようになります。)構成Bの可能性が高いため、構成Aに鉱山があるセルを選択しました。

9回のうち8回、私は正しいでしょう。