Kerasパート6の自動エンコーダー：VAE + GAN

内容

• パート1： はじめに
  
  
• パート2： 多様体学習と潜在変数
  
  
• パート3： 可変可変エンコーダー（ VAE ）
  
  
• パート4： 条件付きVAE
  
  
• パート5： GAN （Generative Adversarial Networks）とテンソルフロー
  
  
• パート6：VAE + GAN
  
  

前の部分では、 CVAE自動エンコーダーを作成し、そのデコーダーは特定のラベルの番号を生成できます。また、特定の画像のスタイルで他のラベルの番号の画像を作成しようとしました。 それはかなりうまくいったが、数字はぼやけて生成された。



最後の部分では、 GANがどのように機能するかを調べて、数字のかなり鮮明な画像を取得しましたが、スタイルをエンコードおよび転送する機能はなくなりました。



このパートでは、 変分オートエンコーダー （ VAE ）と生成競合ネットワーク （ GAN ）を組み合わせることにより、両方のアプローチのベストを取ります 。



後で説明するアプローチは、記事[学習した類似性メトリックを使用したピクセルを超える自動エンコード、Larsen et al、2016]に基づいています。







[1]からの図

復元された画像がぼやけている理由をさらに詳しく調べます。

VAEに関する部分では、画像生成のプロセスが考慮されました 潜在変数から 。

隠し変数の次元 オブジェクトの次元よりも大幅に低い （ VAEの観点では、これらの次元は2と784でした）、また、ある程度のランダム性が常に存在します。 多次元分布が対応する場合があります それは 。 この分布は次のように表すことができます。









どこで 特定の平均的な最も可能性の高いオブジェクト 、そして -ある種の複雑な性質のノイズ。



自動エンコーダーをトレーニングするとき、サンプルからの入力を比較します および自動エンコーダー出力 いくつかのエラー機能を使用する 、









どこで -エンコーダーとデコーダー。



頼む ノイズを定義します 本当のノイズをもたらす 。

最小化 ノイズに適応する自動エンコーダーを教えています それを削除します。つまり、所定のメトリックで平均値を見つけます（2番目の部分では、単純な人工的な例でこれを明確に示しました）。



ノイズが 私たちは機能によって定義します 実際のノイズに対応していません それから 本物から非常に偏っている （例：回帰で実際のノイズがラプラシアンであり、二乗の差が最小化される場合、予測値は外れ値に向かってシフトします）。



写真に戻ります：前の部分の損失を定義するピクセルごとのメトリックと、人間が使用するメトリックがどのように関連しているかを見てみましょう。 [2]の例と図：











上の写真では：

（a）-フィギュアの元の画像、

（b）-（a）から切り取って得たもの、

（c）-半ピクセル右にシフトした数字（a）。



ピクセルごとのメトリックに関して、（a）は（c）よりも（b）にはるかに近い。 人間の知覚の観点からは（b）は数字でさえありませんが、（a）と（b）の違いはほとんど知覚できません。



したがって、ピクセルごとのメトリックを備えた自動エンコーダーは画像をぼかすため、 ：

• 数字の位置は写真の中で少し歩きますが、
  
  
• 数字はわずかに異なって描画されます（ピクセルごとに大きく異なります）。
  
  

人間の知覚の測定基準では、図がすでにぼやけているという事実により、元の図とは非常に異なります。 したがって、人のメトリックを知っているか、そのメトリックに近い場合、それを最適化すると、数字は不明瞭にならず、写真（b）からではなく、完全な数字の重要性が劇的に増加します。



人間により近いメトリックを手動で考え出すことができます。 しかし、 GANアプローチを使用すると、ニューラルネットワーク自体をトレーニングして、適切なメトリックを探すことができます。



最後の部分で書かれたGAN'yについて。

VAEとGANの接続

GANジェネレーターは、 VAEのデコーダーと同様の機能を実行します。前の分布の両方のサンプル に翻訳します 。 ただし、それらには異なる役割があります。デコーダは、学習中に何らかの比較メトリックに依存して、エンコーダによってエンコードされたオブジェクトを復元します。 識別器だけがどの分布を区別できなかった場合、ジェネレーターは何とも比較できないランダムなオブジェクトを生成します または 彼は属します。



アイデア：3番目のネットワークをVAEにディスクリミネーターを追加し、それに入力と復元されたオブジェクトとオリジナルを供給し、 ディスクリミネーターをトレーニングしてどちらがどれかを判断します。





[1]からの図



もちろん、 VAEと同じ比較メトリックを使用することはできません。その理由は、その中で調査すると、デコーダーが元のイメージと簡単に区別できるイメージを生成するためです。 メトリックをまったく使用しないでください-再作成したいので オリジナルのようなもので、 純粋なガンのように。



しかし、これについて考えてみましょう。実際のオブジェクトと生成されたオブジェクトを区別することを学習する弁別器は、一方と他方のいくつかの特徴的な特徴を分離します。 オブジェクトのこれらの機能は、ディスクリミネーターのレイヤーにエンコードされ、それらの組み合わせに基づいて、オブジェクトが実際に存在する可能性が既に与えられます。 たとえば、画像がぼやけている場合、識別器の一部のニューロンは、鮮明な場合よりも多く活性化されます。 さらに、レイヤーが深くなるほど、入力オブジェクトの特性がより詳細にエンコードされます。



各識別レイヤーはオブジェクトの記述コードであり、同時に識別オブジェクトが生成されたオブジェクトを実際のオブジェクトと区別できるようにする特性をエンコードするため、いくつかの単純なメトリック（ピクセルごとなど）を、レイヤーのいずれかのニューロンの活性化に関するメトリックに置き換えることができます：









どこで -有効化 識別器の層 -エンコーダーとデコーダー。



さらに、新しいメトリックが 良くなります。



以下は、著者によって提案された結果のVAE + GANネットワークの図です[1] 。







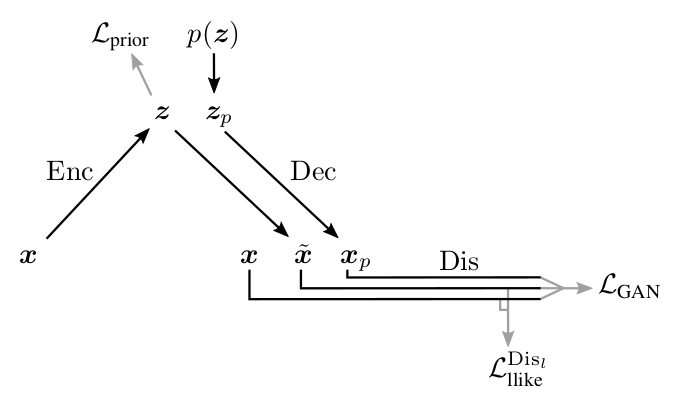
[1]からの図



ここに：

• -入力オブジェクト 、
  
  
• -サンプリング済み から 、
  
  
• -デコーダーによって生成されたオブジェクト 、
  
  
• -復元されたオブジェクト 、
  
  
• -エンコーダーが変換する原因となる損失 必要なものに （ VAEに関するパート3と同じように）、
  
  
• -アクティベーション間のメトリック 弁別層 本当の そして復元された 、
  
  
• -実際のオブジェクト/生成されたオブジェクトのラベルの実際の分布と、予測された弁別器の確率分布の間の相互エントロピー。
  
  

GANと同様に、ネットワークの3つの部分すべてを同時にトレーニングすることはできません。 弁別器は個別にトレーニングする必要があります。特に、弁別器が削減しようとする必要はありません。 、これは0のアクティベーションの差を崩壊させるためです。したがって、すべてのネットワークのトレーニングは関連する損失のみに制限する必要があります。



著者によって提案されたスキーム：









上で、どのネットワークがどのネットワークを学習しているかを確認できます。 おそらくデコーダに特に注意が払われます：一方では、識別器のl番目の層のメトリックで入力と出力の間の距離を短くしようとします（ ）、他方では、差別者をだまそうとしています ） この記事では、著者は、係数を変更することにより、 、ネットワークにとってより重要なものに影響を与えることができます：コンテンツ（ ）またはスタイル（ ） しかし、この効果を観察したとは言えません。

コード

このコードは、以前の部分の純粋なVAEとGANについての内容をほぼ繰り返しています。



繰り返しますが、すぐに条件付きモデルを作成します 。

from IPython.display import clear_output
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns

from keras.layers import Dropout, BatchNormalization, Reshape, Flatten, RepeatVector
from keras.layers import Lambda, Dense, Input, Conv2D, MaxPool2D, UpSampling2D, concatenate
from keras.layers.advanced_activations import LeakyReLU
from keras.layers import Activation
from keras.models import Model, load_model


#    keras
from keras import backend as K
import tensorflow as tf
sess = tf.Session()
K.set_session(sess)


#  
from keras.datasets import mnist
from keras.utils import to_categorical
(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test  = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test  = np.reshape(x_test,  (len(x_test),  28, 28, 1))

y_train_cat = to_categorical(y_train).astype(np.float32)
y_test_cat  = to_categorical(y_test).astype(np.float32)


#  
batch_size = 64
batch_shape = (batch_size, 28, 28, 1)
latent_dim = 8
num_classes = 10
dropout_rate = 0.3
gamma = 1 #  


#     
def gen_batch(x, y):
    n_batches = x.shape[0] // batch_size
    while(True):
        idxs = np.random.permutation(y.shape[0])
        x = x[idxs]
        y = y[idxs]
        for i in range(n_batches):
            yield x[batch_size*i: batch_size*(i+1)], y[batch_size*i: batch_size*(i+1)]

train_batches_it = gen_batch(x_train, y_train_cat)
test_batches_it  = gen_batch(x_test,  y_test_cat)


#  
x_ = tf.placeholder(tf.float32, shape=(None, 28, 28, 1),  name='image')
y_ = tf.placeholder(tf.float32, shape=(None, 10),         name='labels')
z_ = tf.placeholder(tf.float32, shape=(None, latent_dim), name='z')

img = Input(tensor=x_)
lbl = Input(tensor=y_)
z   = Input(tensor=z_)

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

GAN .

def add_units_to_conv2d(conv2, units):
    dim1 = int(conv2.shape[1])
    dim2 = int(conv2.shape[2])
    dimc = int(units.shape[1])
    repeat_n = dim1*dim2
    units_repeat = RepeatVector(repeat_n)(lbl)
    units_repeat = Reshape((dim1, dim2, dimc))(units_repeat)
    return concatenate([conv2, units_repeat])


#   ,  -        (,  - ,  P  P_g   )
def apply_bn_relu_and_dropout(x, bn=False, relu=True, dropout=True):
    if bn:
        x = BatchNormalization(momentum=0.99, scale=False)(x)
    if relu:
        x = LeakyReLU()(x)
    if dropout:
        x = Dropout(dropout_rate)(x)
    return x


with tf.variable_scope('encoder'):
    x = Conv2D(32, kernel_size=(3, 3), strides=(2, 2), padding='same')(img)
    x = apply_bn_relu_and_dropout(x)
    x = MaxPool2D((2, 2), padding='same')(x)

    x = Conv2D(64, kernel_size=(3, 3), padding='same')(x)
    x = apply_bn_relu_and_dropout(x)

    x = Flatten()(x)
    x = concatenate([x, lbl])
    
    h = Dense(64)(x)
    h = apply_bn_relu_and_dropout(h)

    z_mean    = Dense(latent_dim)(h)
    z_log_var = Dense(latent_dim)(h)

    def sampling(args):
        z_mean, z_log_var = args
        epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0., stddev=1.0)
        return z_mean + K.exp(K.clip(z_log_var/2, -2, 2)) * epsilon
    l = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
encoder = Model([img, lbl], [z_mean, z_log_var, l], name='Encoder')


with tf.variable_scope('decoder'):
    x = concatenate([z, lbl])
    x = Dense(7*7*128)(x)
    x = apply_bn_relu_and_dropout(x)
    x = Reshape((7, 7, 128))(x)
    x = UpSampling2D(size=(2, 2))(x)

    x = Conv2D(64, kernel_size=(5, 5), padding='same')(x)
    x = apply_bn_relu_and_dropout(x)

    x = Conv2D(32, kernel_size=(3, 3), padding='same')(x)
    x = UpSampling2D(size=(2, 2))(x)
    x = apply_bn_relu_and_dropout(x)
    
    decoded = Conv2D(1, kernel_size=(5, 5), activation='sigmoid', padding='same')(x)
decoder = Model([z, lbl], decoded, name='Decoder')


with tf.variable_scope('discrim'):
    x = Conv2D(128, kernel_size=(7, 7), strides=(2, 2), padding='same')(img)
    x = MaxPool2D((2, 2), padding='same')(x)
    x = apply_bn_relu_and_dropout(x)
    x = add_units_to_conv2d(x, lbl)

    x = Conv2D(64, kernel_size=(3, 3), padding='same')(x)
    x = MaxPool2D((2, 2), padding='same')(x)
    x = apply_bn_relu_and_dropout(x)

    # l-     
    l = Conv2D(16, kernel_size=(3, 3), padding='same')(x)
    x = apply_bn_relu_and_dropout(x)

    h = Flatten()(x)
    d = Dense(1, activation='sigmoid')(h)
discrim = Model([img, lbl], [d, l], name='Discriminator')

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

z_mean, z_log_var, encoded_img = encoder([img, lbl])

decoded_img = decoder([encoded_img, lbl])
decoded_z   = decoder([z,           lbl])

discr_img,     discr_l_img     = discrim([img,         lbl])
discr_dec_img, discr_l_dec_img = discrim([decoded_img, lbl])
discr_dec_z,   discr_l_dec_z   = discrim([decoded_z,   lbl])

cvae_model = Model([img, lbl], decoder([encoded_img, lbl]), name='cvae')
cvae =  cvae_model([img, lbl])

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:



, , MSE, -.

#  
L_prior = -0.5*tf.reduce_sum(1. + tf.clip_by_value(z_log_var, -2, 2) - tf.square(z_mean) - tf.exp(tf.clip_by_value(z_log_var, -2, 2)))/28/28

log_dis_img     = tf.log(discr_img + 1e-10)
log_dis_dec_z   = tf.log(1. - discr_dec_z + 1e-10)
log_dis_dec_img = tf.log(1. - discr_dec_img + 1e-10)

L_GAN = -1/4*tf.reduce_sum(log_dis_img + 2*log_dis_dec_z + log_dis_dec_img)/28/28

# L_dis_llike = tf.reduce_sum(tf.square(discr_l_img - discr_l_dec_img))/28/28
L_dis_llike = tf.reduce_sum(tf.nn.sigmoid_cross_entropy_with_logits(labels=tf.sigmoid(discr_l_img),
                                                                    logits=discr_l_dec_img))/28/28


#  , , 
L_enc = L_dis_llike + L_prior 
L_dec = gamma * L_dis_llike - L_GAN
L_dis = L_GAN


#   
optimizer_enc = tf.train.RMSPropOptimizer(0.001)
optimizer_dec = tf.train.RMSPropOptimizer(0.0003)
optimizer_dis = tf.train.RMSPropOptimizer(0.001)

encoder_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, "encoder")
decoder_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, "decoder")
discrim_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, "discrim")

step_enc = optimizer_enc.minimize(L_enc, var_list=encoder_vars)
step_dec = optimizer_dec.minimize(L_dec, var_list=decoder_vars)
step_dis = optimizer_dis.minimize(L_dis, var_list=discrim_vars)


def step(image, label, zp):
    l_prior, dec_image, l_dis_llike, l_gan, _, _ = sess.run([L_prior, decoded_z, L_dis_llike, L_GAN, step_enc, step_dec],
                                                            feed_dict={z:zp, img:image, lbl:label, K.learning_phase():1})
    return l_prior, dec_image, l_dis_llike, l_gan

def step_d(image, label, zp):
    l_gan, _ = sess.run([L_GAN, step_dis], feed_dict={z:zp, img:image, lbl:label, K.learning_phase():1})
    return l_gan


      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:





:

sess.run(tf.global_variables_initializer())

nb_step = 3 #     

batches_per_period = 3
for i in range(48000):
    print('.', end='')

    #   
    for j in range(nb_step):
        b0, b1 = next(train_batches_it)
        zp = np.random.randn(batch_size, latent_dim)
        l_g = step_d(b0, b1, zp)
        if l_g < 1.0:
            break
        
    #     
    for j in range(nb_step):
        l_p, zx, l_d, l_g = step(b0, b1, zp)
        if l_g > 0.4:
            break
        b0, b1 = next(train_batches_it)
        zp = np.random.randn(batch_size, latent_dim)

    #   
    if not i % batches_per_period:
        period = i // batches_per_period
        if period in save_periods:
            on_n_period(period)
        print(i, l_p, l_d, l_g)

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:





, :

CVAE

, .



CVAE, — 2





CVAE+GAN, — 2





CVAE+GAN, — 8





:

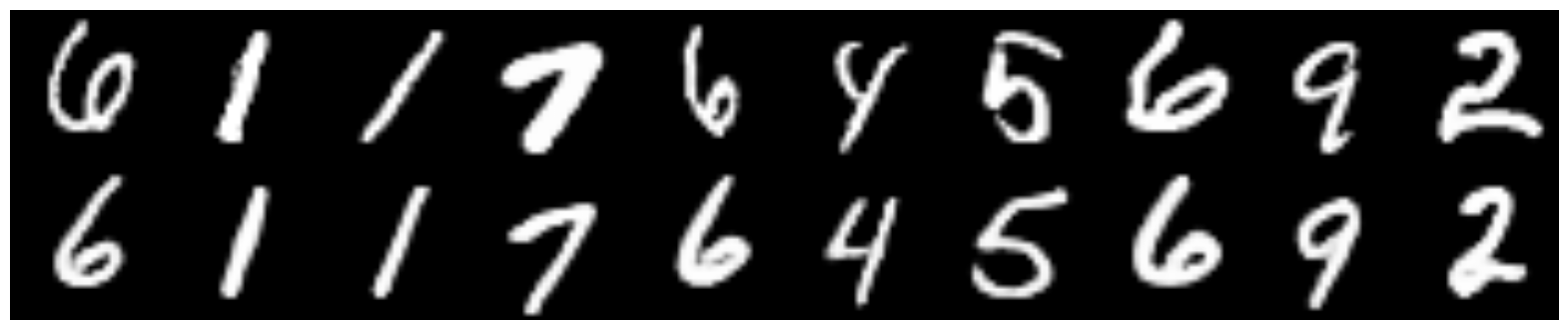
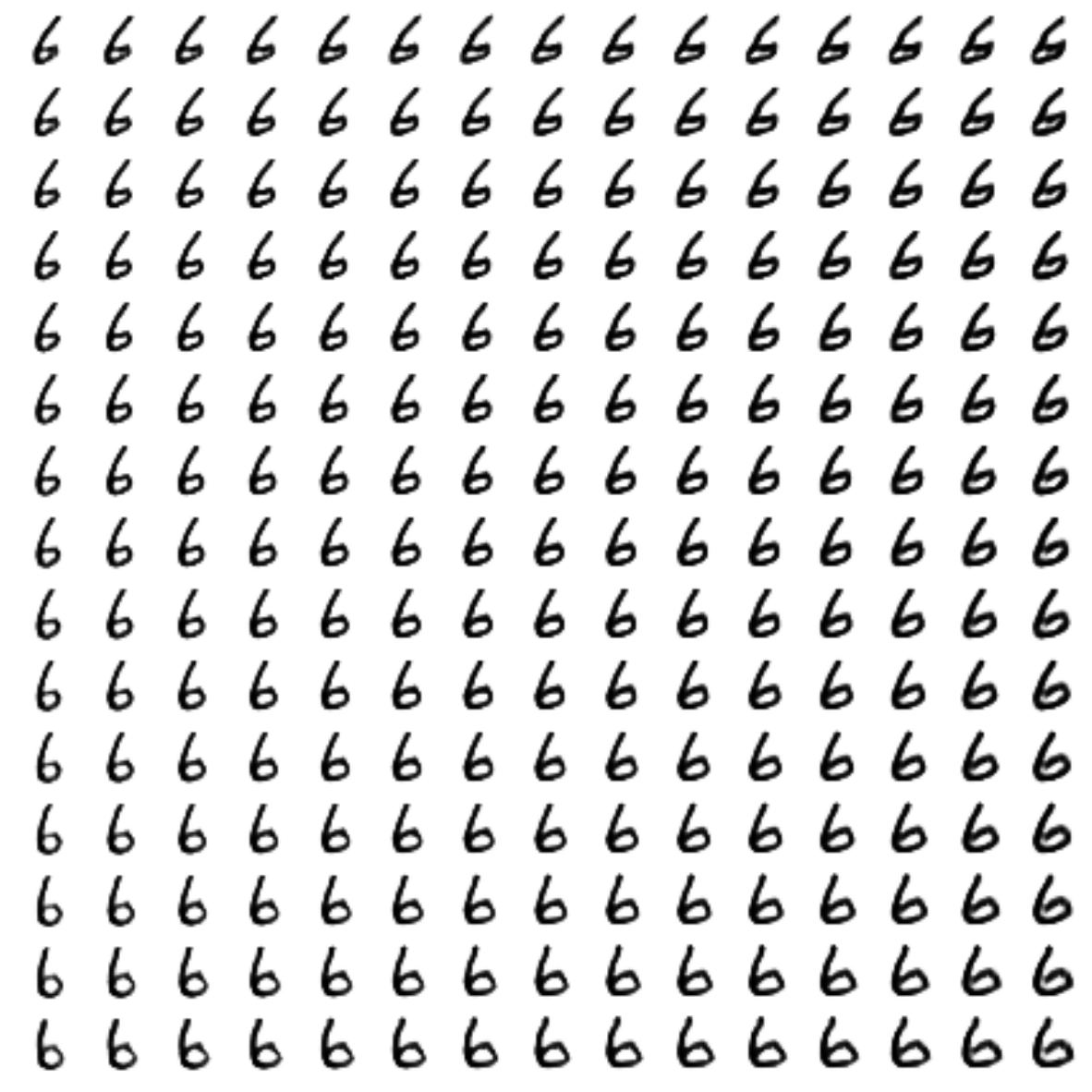
«7», ( ).



CVAE:





:

, . , , VAE, GAN, , conditional , .

keras’ tensorflow.



, !

:

[1] Autoencoding beyond pixels using a learned similarity metric, Larsen et al, 2016, https://arxiv.org/abs/1512.09300



VAE:

[2] Tutorial on Variational Autoencoders, Carl Doersch, 2016, https://arxiv.org/abs/1606.05908



keras tensorflow:

[3] https://blog.keras.io/keras-as-a-simplified-interface-to-tensorflow-tutorial.html