
実践によって確認された理論以上に、研究に役立つツールはありません。
なぜ測定の情報理論が必要なのですか?
前の出版物[1]では、統計的サンプルのデータに応じてランダム変数の分布の法則の選択を検討し、測定誤差の分析への情報アプローチのみに言及しました。 したがって、この緊急のトピックの議論を続けます。
測定結果の分析に対する情報アプローチの利点は、ランダム誤差の分布の法則について、不確実性のエントロピー間隔のサイズを見つけることができることです。 これにより、信頼値の任意の選択による「誤解」が排除されます。
さらに、サンプルの確率的特性と情報特性を組み合わせることにより、ランダムエラーの分布の性質をより正確に判断できます。 これは、さまざまな分布法則とその重ね合わせのエントロピー係数や矛盾などのパラメーターの数値の広範なデータベースによって説明されます。
情報分析および確率分析の本質について
ここでのキーワードは、不確実性という言葉です。 測定はプロセスと見なされ、その結果、測定量に関する情報の初期の不確実性-xが減少します。 H(X) - 不確実性の定量的測定は、エントロピーです 。 より多くの場合、ランダム変数x1、x2 ... xnの離散値に遭遇します。これは、コンピューターテクノロジーが広く使用されているためです。 そのような数量については、多くを説明する1つの式のみを記述します。
ここで、p_i-は、確率変数xが値x_iをとった確率です。 0≤p_i≤1であり、同時にlgp_i<0であるため、H(x)≥0を取得するには、式の合計の前にマイナス記号が付きます。
エントロピーは情報の単位で測定されます。 上記の式の情報の単位は、対数の底に依存します。 このDITの対数のため。 自然対数- ニット。 明白な理由のために、最も一般的に\エントロピーはビット単位で測定されるS内の二進対数を用います。
測定の過程で、xの知識が増加するにつれて、xの初期不確実性は減少します。 ただし、測定後、測定誤差∆に関連する残留不確実性H(∆)が残ります。
残留エントロピーH(∆)は、上記の式で決定できます。xの代わりに誤差∆を代入し、中間計算を省略して、分布則の誤差∆のエントロピー値を取得します。
測定結果から誤差のエントロピー値を取得する方法
これを行うには、まず、ランダムエラーの離散値のシーケンスを間隔に分割し、次に各間隔に該当するこれらの値の頻度をカウントする必要があります。 間隔内で、これらのエラー値が発生する確率は、この間隔に入る頻度と測定された測定の数の比率に等しい定数であると想定されます。
つまり、matplotlibライブラリのhist()チャート関数が実行する手順の一部を再現する必要があります。 結果の図をhist()を使用して取得した図と比較して、次の簡単な手順でこれを示しましょう。
データ処理方法を比較するためのプログラム
import matplotlib.pyplot as plt import numpy as np from scipy.stats import uniform def diagram(a): a.sort()# n=len(a)# m= int(10+np.sqrt(n))# d=(max(a)-min(a))/m# x=[];y=[] for i in np.arange(0,m,1): x.append(min(a)+d*i)# k=0 for j in a: if min(a)+d*i <=j<min(a)+d*(i+1): k=k+1 y.append(k)# plt.title(" ") plt.bar(x,y, d) plt.grid(True) plt.show() plt.title(" hist()") plt.hist(a,m) plt.grid(True) plt.show() a=uniform.rvs(size=500) # diagram(a)
結果の図を比較します。
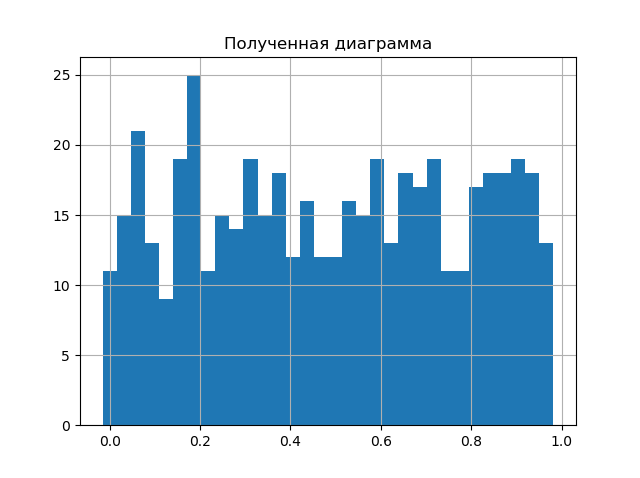
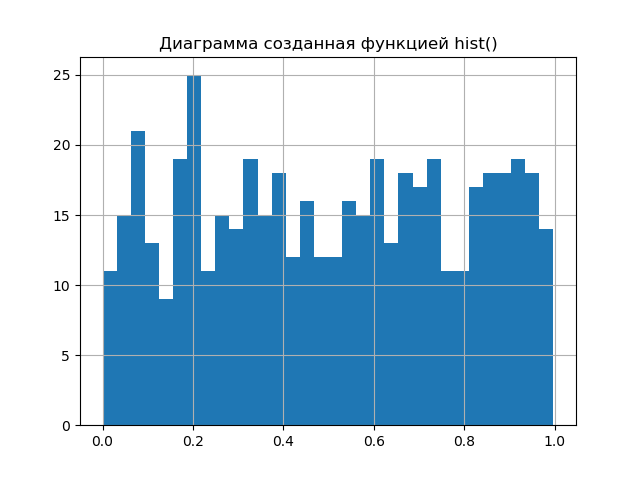
ダイアグラムはほぼ同じであり、hist()関数よりも1大きいため、ブレーク間隔の数は分析結果を改善するだけです。 したがって、エントロピー誤差値を取得する第2段階に進むことができます;このために、[2]で与えられ、関係(2)から得られた関係を使用します。
上記のリストでは、xのリストには間隔の境界の値が含まれ、yのリストにはこれらの間隔のエラーの値の頻度が含まれています。 Pythonリスト文字列の(3)を書き換えます。
h = 0.5 * d * n * 10 **(-sum([w * np.log10(w)for w in y if w!= 0])/ n)
私たちの問題の解決を完了するために、我々はエントロピー係数Kとkontrekstsessa のpsiの2つの以上の値を必要とする、[2]にそれらを取るが、我々は、Pythonのために書くことができます。
k = h / np.std(a)
mu4 =合計([(w-np.mean(a))** 4 for w in a])/ n
上記の4行をリストに追加することは残りますが、最終結果を分析するには、もう1つの重要な問題を考慮する必要があります。
エントロピー係数と反過剰を使用して、誤差の分布の法則を分類するにはどうすればよいですか
確率理論によると、分布則の形式は、相対的な4次モーメントまたは反インシデントによって特徴付けられます。 情報理論では、分布則の形式はエントロピー係数の値によって決まります。 上記を考えると、psi、k平面上に、与えられた分布則に対応する点を配置します。 しかし、最初に、エラー分布の5つの最も重要な法則の値psi、k、および図を取得します。
数値psi、kを取得してプロットするプログラム
import matplotlib.pyplot as plt import numpy as np from scipy.stats import logistic,norm,uniform,erlang,pareto,cauchy def diagram(a,nr): a.sort() n=len(a) m= int(10+np.sqrt(n)) d=(max(a)-min(a))/m x=[];y=[] for i in np.arange(0,m,1): x.append(min(a)+d*i) k=0 for j in a: if min(a)+d*i <=j<min(a)+d*(i+1): k=k+1 y.append(k) h=0.5*d*n*10**(-sum([w*np.log10(w) for w in y if w!=0])/n) k=h/np.std (a) mu4=sum ([(w-np.mean (a))**4 for w in a])/n psi=(np.std(a))**2/np.sqrt(mu4) plt.title("%s : k=%s; psi=%s; h=%s."%(nr,str(round(k,3)),str(round(psi,3)),str(round(h,3)))) plt.bar(x,y, d) plt.grid(True) plt.show() nr=" " a=uniform.rvs( size=1000) diagram(a,nr) nr=" " a=logistic.rvs( size=1000) diagram(a,nr) nr=" " a=norm.rvs( size=1000) diagram(a,nr) nr=" " a = erlang.rvs(4,size=1000) diagram(a,nr) nr=" " a = pareto.rvs(4,size=1000) diagram(a,nr) nr=" " a = cauchy.rvs(size=1000) diagram(a,nr)
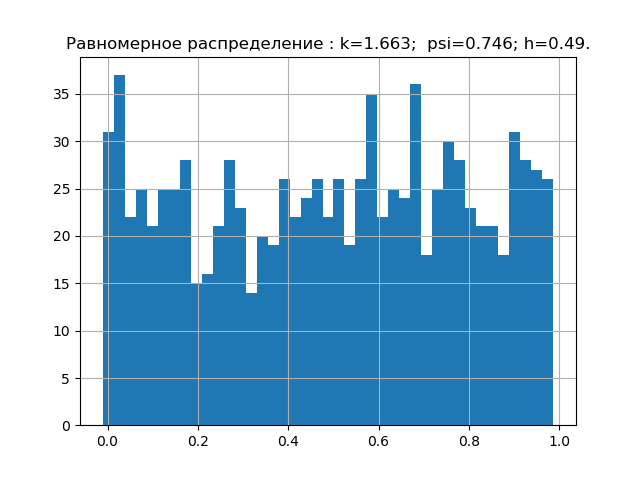
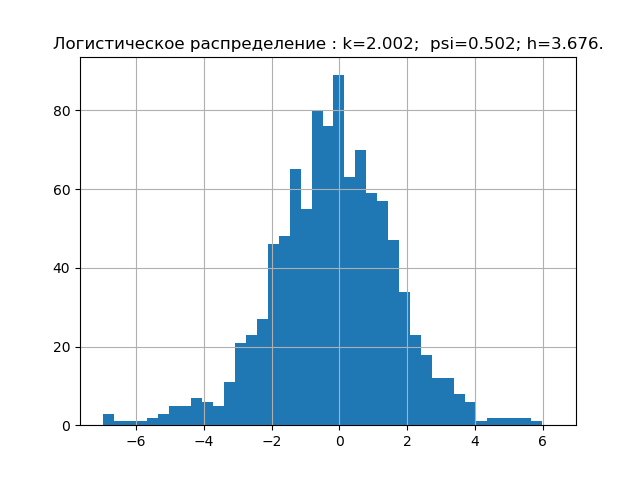
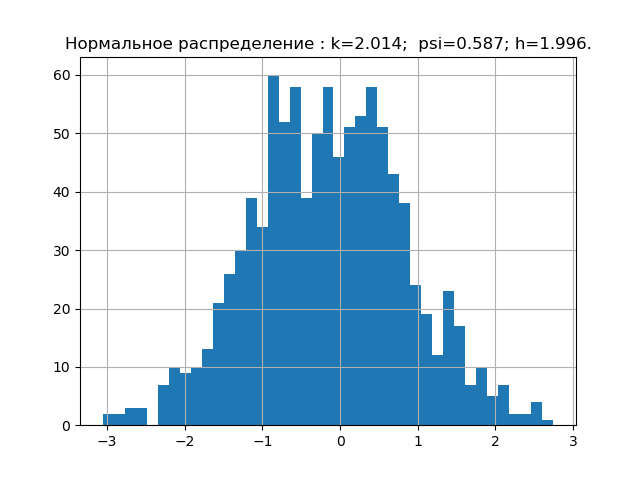
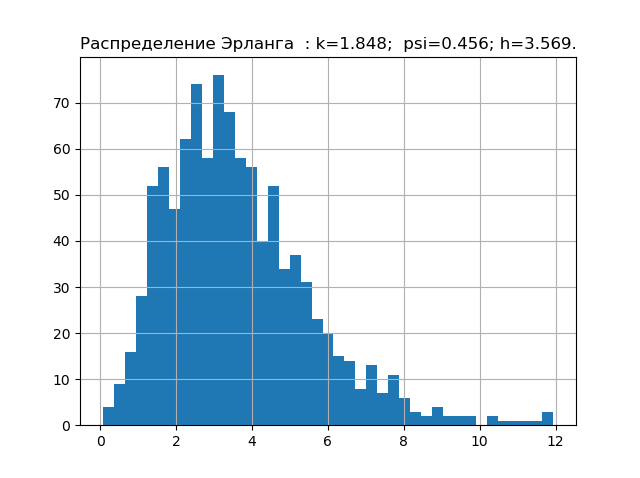
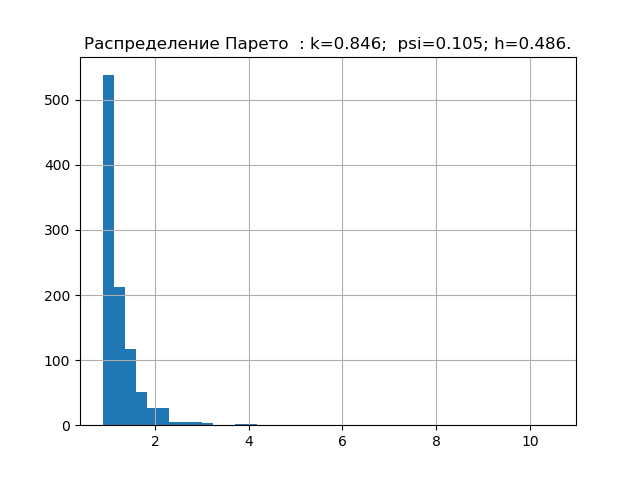
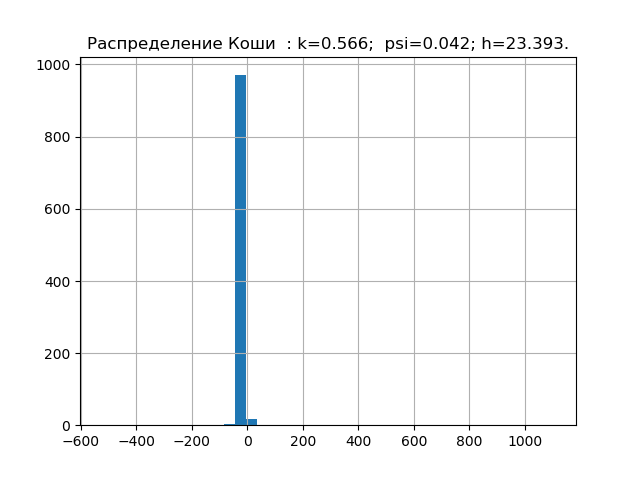
すでに収集した誤差の分布の法則のエントロピー特性の最小ベース。 次に、例えば、未知の分布則を持つサンプルの理論を確認します。
a = [0.203、0.154、0.172、0.192、0.233、0.181、0.219、0.153、0.168、0.132、0.204、0.165、0.197、0.205、0.143、0.201、0.168、0.147、0.208、0.195、0.153、0.193、0.178、0.162 、0.157、0.228、0.219、0.125、0.101、0.211、0.183、0.147、0.145、0.181、0.184、0.139、0.198、0.185、0.202、0.238、0.167、0.204、0.195、0.172、0.196、0.178、0.213、0.175、0.194 、0.178、0.135、0.178、0.118、0.186、0.191]
誰かが興味を持っている場合は、いずれかを選択して確認できます。 このサンプルでは、次の図とパラメーターを示します。
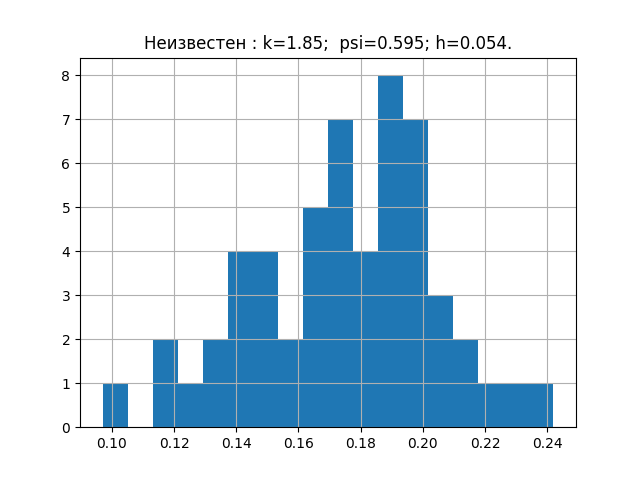
ここで、受信したパラメーターをチャートに転送します。
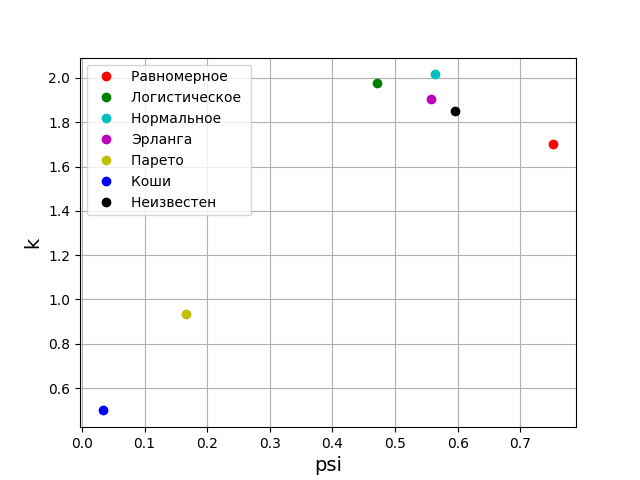
グラフから、調査中のサンプルの分布則がアーラン分布則に最も近いことがわかります。
おわりに
この出版物で議論されている測定の情報理論の要素のPythonでの実装があなたにとって興味のないものになることを願っています。
ご清聴ありがとうございました!