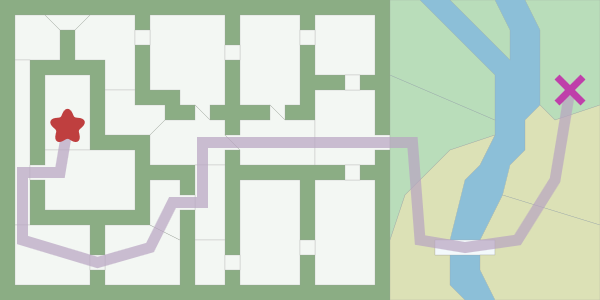
このパスを検索するには、マップがグラフの場合に適用できるグラフ検索アルゴリズムを使用できます。 *は、多くの場合、グラフ検索アルゴリズムとして使用されます。 幅優先検索は、グラフ検索アルゴリズムの中で最も単純なものなので、それから始めて、徐々にA *に進みましょう。
地図表示
アルゴリズムを学習するときに最初に必要なことは、 データを理解することです。 入り口で何が出されますか? 私たちは何を逃げ出しますか?
入力 :A *を含むグラフ検索アルゴリズムは、入力としてグラフを受け取ります。 グラフは、ポイント(「ノード」)とそれらの間の接続(「エッジ」)のセットです。 A *に渡したグラフは次のとおりです。

*は他には何も見えません。 彼はカウントだけを見ています。 彼は何かが部屋の中にあるのか外にあるのか、それがドアなのか部屋なのか、面積の大きさを知りません。 彼はカウントだけを見ています! 彼は一番上のカードとこれとの違いを理解していません。
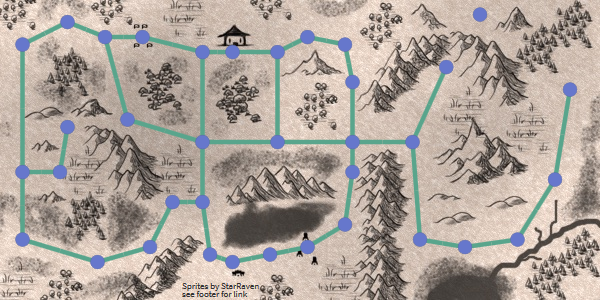
出力 :*定義されたパスは、ノードとエッジで構成されます。 bs骨は抽象的な数学的概念です。 *は、あるポイントから別のポイントに移動する必要があることを示していますが、その方法は示していません。 彼は部屋やドアについて何も知らないことを覚えておいてください、彼はカウントだけを見ます。 A *によって返されるグラフのエッジを自分で決定する必要があります-タイルからタイルへ移動、直線移動、ドアを開け、曲線状のパスに沿って移動します。
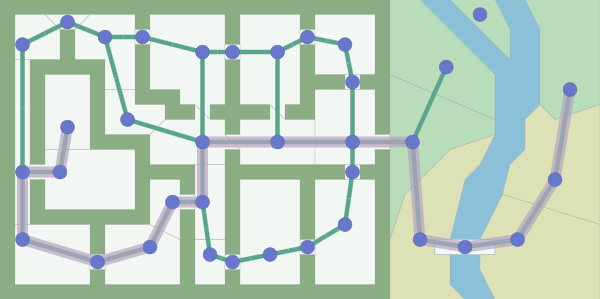
トレードオフ:各ゲームカードには、パス検索グラフをA *アルゴリズムに渡すさまざまな方法があります。 上の図のマップは、ドアをノードに変えます。
しかし、ドアをリブに変えるとどうなりますか?

そして、グリッドを使用してパスを見つけるとどうなりますか?
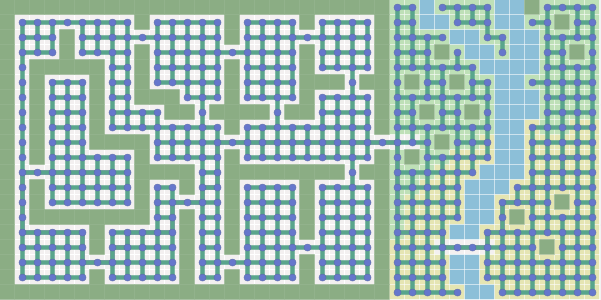
パス検索グラフは、ゲームマップで使用されているものと同じである必要はありません。 グリッドベースのマップでは、メッシュなしでパス検索グラフを使用できます。逆も同様です。 *は、グラフノードの最小数でより高速に実行されます。 多くの場合、グリッドは操作が簡単ですが、多くのノードを生成します。 この記事では、グラフ設計ではなく、A *アルゴリズム自体について説明します。 グラフの詳細については、 他のページをご覧ください 。 さらに説明するために、 概念を視覚化する方が簡単なので 、将来グリッドを使用します 。
アルゴリズム
グラフを扱う多くのアルゴリズムがあります。 私は以下を検討します:

幅優先検索は、すべての方向で均一に実行されます。 これは、通常のパスの検索だけでなく、マップの手順生成、フローパスの検索、距離マップ、および他のタイプのマップ分析にも非常に便利なアルゴリズムです。

ダイクストラのアルゴリズム (均一コスト検索とも呼ばれます)を使用すると、パスの調査に優先順位を付けることができます。 すべての可能なパスを均等に探索するのではなく、低コストのパスを好みます。 アルゴリズムが道路に沿って移動するようにコストを削減し、コストを増加させて、森林や敵を回避することができます。 移動コストが異なる場合、幅を検索する代わりに使用します。

*は、単一のエンドポイント用に最適化されたダイクストラのアルゴリズムの修正です。 ダイクストラのアルゴリズムはすべてのポイントへのパスを見つけることができ、A *は1つのポイントへのパスを見つけます。 彼は、ゴールに近づく道を優先します。
最も単純な-幅優先検索から始め、関数を追加して、徐々にそれをA *に変えていきます。
広い検索
これらすべてのアルゴリズムの重要な考え方は、 境界と呼ばれる拡大するリングの状態を追跡することです。 グリッドでは、このプロセスはフラッドフィルと呼ばれることもありますが、グリッドを持たないカードにも同じ手法が適用されます。 境界線拡張アニメーションを見る:
これを実装する方法は? 境界線が空になるまで、これらの手順を繰り返します。
- 境界線からポイントを選択して削除します 。
- 再度処理する必要がないことを知るために、ポイントを訪問済みとしてマークします。
- 国境を拡大し、その隣人を見ます。 まだ見たことのない隣人をすべて国境に追加します。
これを詳しく見てみましょう。 タイルには、訪問した順に番号が付けられます。
このアルゴリズムは、Pythonコードのわずか10行で説明されています。
frontier = Queue() frontier.put(start ) visited = {} visited[start] = True while not frontier.empty(): current = frontier.get() for next in graph.neighbors(current): if next not in visited: frontier.put(next) visited[next] = True
このサイクルには、A *を含むこの記事のグラフの検索アルゴリズムの本質が含まれています。 しかし、最短経路をどのようにして見つけるのでしょうか? サイクルは実際にパスを作成するのではなく、マップ上のすべてのポイントを訪問する方法を指示するだけです。 これは、幅優先検索が単なるパス検索以外にも使用できるためです。 この記事では、タワーディフェンスゲームでの使用方法を示しますが、距離マップ、手続き型マップの生成などにも使用できます。 ただし、ここではパスを見つけるために使用したいので、ループを変更して、訪問したすべてのポイントの元の場所を追跡し、
visited
を
came_from
変更し
came_from
。
frontier = Queue() frontier.put(start ) came_from = {} came_from[start] = None while not frontier.empty(): current = frontier.get() for next in graph.neighbors(current): if next not in came_from: frontier.put(next) came_from[next] = current
ここで、各ポイントのcame_fromは、来た場所を示します。 これは、おとぎ話のパン粉のようなものです。 これでパス全体を再作成できます。 矢印が開始位置への戻り経路をどのように示しているかを確認してください。
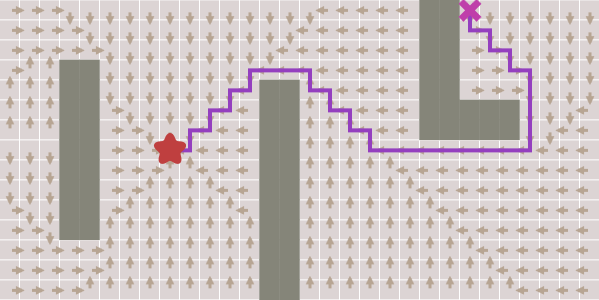
パスを再作成するコードは簡単です。 ターゲットから先頭に戻る矢印に従ってください。 パスはエッジのシーケンスですが 、ノードのみを保存する方が簡単な場合があります。
current = goal path = [current] while current != start: current = came_from[current] path.append(current) path.append(start) # optional path.reverse() # optional
これは、最も単純なパス検索アルゴリズムです。 上記のようにグリッドだけでなく、グラフ構造でも機能します。 ダンジョンでは、グラフ内のポイントが部屋になり、エッジがそれらの間のドアになることがあります。 プラットフォーマーでは、グラフのノードは場所になり、エッジは可能なアクションになります。左に移動、右に移動、ジャンプ、下にジャンプします。 一般的に、グラフは状態と状態を変更するアクションとして認識することができます。 ここで地図の提示についてもっと書きました 。 この記事の残りの部分では、引き続きメッシュを使用した例を使用し、幅の検索のバリエーションを使用できる理由について説明します。
早期退出
1つのポイントから他のすべてのポイントへのパスを見つけました。 多くの場合、すべてのパスが必要なわけではなく、2つのポイント間のパスが必要なだけです。 目標を見つけたらすぐに、国境の拡大をやめることができます。 ターゲットを見つけた後、境界がどのように拡大するのを止めるかを見てください。
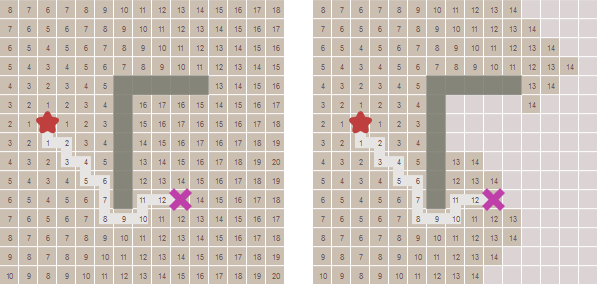
コードはかなり簡単です:
frontier = Queue() frontier.put(start ) came_from = {} came_from[start] = None while not frontier.empty(): current = frontier.get() if current == goal: break for next in graph.neighbors(current): if next not in came_from: frontier.put(next) came_from[next] = current
引越費用
これまでのところ、同じ値で対策を講じてきました。 場合によっては、さまざまなタイプの移動のパスを見つけるのにさまざまなコストがかかります。 たとえば、文明では、平野または砂漠の移動には1移動ポイント、森林の移動には5移動ポイントがかかる場合があります。 記事の冒頭の地図では、水を通過することは草に沿って移動するよりも10倍の費用がかかります。 別の例は、グリッド内の斜めの動きです。これは、軸に沿った動きよりもコストがかかります。 このコストを考慮するには、パス検索が必要です。 最初からのステップ数を最初からの距離と比較してみましょう。

これを行うには、 ダイクストラのアルゴリズム (均一コスト検索とも呼ばれます)が必要です。 幅優先検索とはどう違いますか? 移動コストを追跡する必要があるため、新しい変数
cost_so_far
を追加して、開始点からの移動の総コストを監視します。 ポイントを評価するとき、移動のコストを考慮する必要があります。 キューを優先キューに変えましょう。 あまり明らかではありませんが、1つのポイントが異なるコストで複数回アクセスされる可能性があるため、ロジックをわずかに変更する必要があります。 一度もポイントにアクセスしたことがないときに境界にポイントを追加する代わりに、ポイントへの新しいパスが以前の最良のパスよりも優れている場合にポイントを追加します。
frontier = PriorityQueue() frontier.put(start, 0) came_from = {} cost_so_far = {} came_from[start] = None cost_so_far[start] = 0 while not frontier.empty(): current = frontier.get() if current == goal: break for next in graph.neighbors(current): new_cost = cost_so_far[current] + graph.cost(current, next) if next not in cost_so_far or new_cost < cost_so_far[next]: cost_so_far[next] = new_cost priority = new_cost frontier.put(next, priority) came_from[next] = current
通常のキューの代わりに優先キューを使用すると、境界線の拡大方法が変わります。 等高線を使用すると、これを確認できます。 ビデオを見て、境界線が森林を通ってよりゆっくりと拡大する様子を見てください。最短経路は、中央の森林ではなく、中央の森林の周囲で検索されます。
1とは異なる移動コストにより、グリッドだけでなく、より興味深いグラフを探索できます。 記事の冒頭の地図では、移動コストは部屋間の距離に基づいています。 移動コストは、敵または味方の近接度に基づいてエリアを回避または優先するためにも使用できます。 興味深い実装の詳細:通常の優先度キューは挿入および削除操作をサポートしますが、Dijkstraのアルゴリズムの一部のバージョンは、優先度キューに既にある要素の優先度を変更する3番目の操作も使用します。 この操作は使用せず、アルゴリズムの実装ページで説明します 。
発見的検索
幅優先探索とダイクストラのアルゴリズムでは、境界線はすべての方向に拡大します。 すべてのポイントまたは多くのポイントへの道を探している場合、これは論理的な選択です。 ただし、通常、検索は1つのポイントに対してのみ実行されます。 境界線を他の方向よりも目標に向かって拡大させましょう。 最初に、目標にどれだけ近いかを示すヒューリスティック関数を定義します。
def heuristic(a, b): # Manhattan distance on a square grid return abs(ax - bx) + abs(ay - by)
ダイクストラのアルゴリズムでは、 最初からの距離を使用して優先度キューを並べました。 優先順位の最初の最適一致の貪欲な検索では、代わりにターゲットまでの推定距離を使用します。 ターゲットに最も近いポイントが最初に検査されます。 コードは幅優先検索の優先順位を持つキューを使用しますが、ダイクストラのアルゴリズムの
cost_so_far
は適用しません。
frontier = PriorityQueue() frontier.put(start, 0) came_from = {} came_from[start] = None while not frontier.empty(): current = frontier.get() if current == goal: break for next in graph.neighbors(current): if next not in came_from: priority = heuristic(goal, next) frontier.put(next, priority) came_from[next] = current
仕組みを見てみましょう。
わあ! すごいですね しかし、より複雑なマップではどうなりますか?
これらのパスは最短ではありません。 そのため、このアルゴリズムは障害物があまり多くない場合に高速に動作しますが、パスは最適ではありません。 これは修正できますか? もちろん。
アルゴリズムA *
ダイクストラのアルゴリズムは最短経路を見つけるのに適していますが、彼はすべての方向、見込みのない方向を探索することに時間を費やしています。 貪欲検索は有望な方向を探索しますが、最短経路を見つけられない場合があります。 A *アルゴリズムは、開始からの真の距離とターゲットまでの推定距離の両方を使用します。
コードはダイクストラのアルゴリズムに非常に似ています:
frontier = PriorityQueue() frontier.put(start, 0) came_from = {} cost_so_far = {} came_from[start] = None cost_so_far[start] = 0 while not frontier.empty(): current = frontier.get() if current == goal: break for next in graph.neighbors(current): new_cost = cost_so_far[current] + graph.cost(current, next) if next not in cost_so_far or new_cost < cost_so_far[next]: cost_so_far[next] = new_cost priority = new_cost + heuristic(goal, next) frontier.put(next, priority) came_from[next] = current
アルゴリズムの比較 :ダイクストラのアルゴリズムは、開始点からの距離を計算します。 最初の最適一致の貪欲な検索では、ターゲットポイントまでの距離が推定されます。 *は、これら2つの距離の合計を使用します。
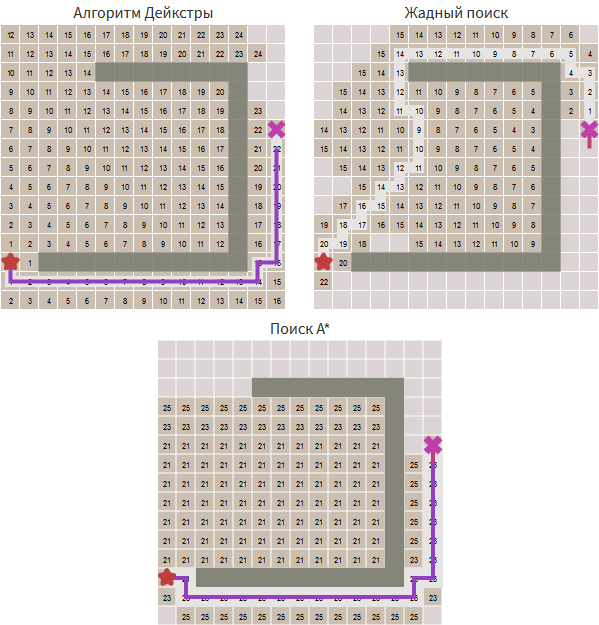
元の記事の壁のさまざまな場所に穴を開けてみてください 。 貪欲な検索は正しい答えを見つけ、A *もそれを見つけ、同じエリアを探索します。 最初のベストの貪欲な検索が間違った答え(長いパス)を見つけると、A *はダイクストラのアルゴリズムのように正しいものを見つけますが、ダイクストラのアルゴリズムよりも調査しません。
*は、2つのアルゴリズムから最適なものを取ります。 ヒューリスティックは距離を再評価しないため、A * は適切な答えを見つけるためにヒューリスティックを使用しません 。 彼は、ダイクストラアルゴリズムのような最適なパスを見つけます。 *は、ヒューリスティックを使用してノードの順序を変更し、ターゲットノードをより早く見つける可能性を高めます。
そして...それだけです! これはアルゴリズムA *です。
追加の読書
実装する準備はできていますか? 既製のライブラリを使用してみてください。 自分で実装したい場合は、Python、C ++、C#でグラフ、キュー、パス検索アルゴリズムを段階的に実装するための手順があります。
ゲームマップ上のパスを見つけるには、どのアルゴリズムを使用する必要がありますか?
- すべてのポイントからまたはすべてのポイントへのパスを見つける必要がある場合は、幅優先探索またはダイクストラのアルゴリズムを使用します。 トラフィックのコストが同じ場合、幅優先検索を使用します。 移動のコストが変化する場合は、ダイクストラのアルゴリズムを使用してください。
- 1つのポイントへの道を見つける必要がある場合は、欲張りな検索を使用して、最初のベストまたはA *を探します。 ほとんどの場合、A *を優先する必要があります。 貪欲な検索を使用したい場合は、 「無効な」ヒューリスティックで A *を使用することを検討してください。
最善の方法はどうですか? 幅優先探索とダイクストラのアルゴリズムは、グラフ内の最短経路を見つけることが保証されています。 貪欲な検索は必ずしもそれを見つけるとは限りません。 ヒューリスティックが真の距離より大きくならない場合、*は最短パスを見つけることが保証されます。 ヒューリスティックが小さくなると、A *はダイクストラのアルゴリズムになります。 ヒューリスティックが大きくなると、A *は最適な最初の一致を求める貪欲な検索に変わります。
パフォーマンスはどうですか? グラフ内の不要なポイントを削除することをお勧めします。 グリッドを使用する場合は、これをお読みください 。 グラフのサイズを小さくすると、すべてのグラフ検索アルゴリズムが役立ちます。 その後、可能な限り単純なアルゴリズムを使用します。 シンプルキューはより高速に実行されます。 貪欲な検索は通常、ダイクストラのアルゴリズムよりも高速ですが、最適なパスを提供しません。 ほとんどのパス検索タスクでは、最良の選択はA *です。
地図上以外での使用はどうですか? 記事でマップを使用したのは、マップのアルゴリズムの操作を説明する方が簡単だと思うからです。 ただし、これらのグラフ検索アルゴリズムは、ゲームカードだけでなく、どのグラフでも使用でき、アルゴリズムコードを2次元グリッドに依存しない形式で表示することを試みました。 マップ上の移動のコストは、グラフのエッジの任意の重みに変わります。 ヒューリスティックを任意のカードに転送するのはそれほど簡単ではないため、グラフのタイプごとにヒューリスティックを作成する必要があります。 フラットマップの場合、距離が適切な選択であるため、ここでは距離を使用しました。
ここでパスを見つけることについてもっと書いた。 グラフ検索は必要なものの一部にすぎないことに注意してください。 A *だけでは、関節の動き、障害物の移動、地図の変更、危険な領域の評価、フォーメーション、旋回半径、オブジェクトサイズ、アニメーション、パスのスムージングなどを処理しません。