準備ができた例
この例は、OpenGlobusエンジンに基づいています。この場合は、純粋なJavascript WebGLのラッパーとして使用されます。
(申し訳ありませんが、まだ動作しません)
-2Dケースの例
-3Dケースの例 (キーW、S、A、D、Q、Eおよびカーソルを使用して移動)
エントリー
地図作成ライブラリを作成する過程で、太さの異なる線を描画できるツールが必要でした。 もちろん、WebGLには線描画メカニズムがありますが、残念ながら線の太さを設定することはできません。 したがって、ポリゴンを使用して線を描画する必要があります。三角形を使用することをお勧めします。 インターネットでは、回線を「三角測量」する方法、これでどのような困難が生じるか、およびそれらを解決する方法に関するいくつかの優れた記事を見つけることができます。 残念ながら、コードをコピーしてシェーダーで使用できる記事は見つかりませんでした。
鉛筆と紙を使ってアルゴリズムの描画に何時間も費やした後、完全に洗練されたglslシェーダーのデバッグに何時間も費やした後、私は最終的にはるかに高速に達成できる結果に至りました。 以下で説明するWebGLで折れ線をレンダリングするアプローチがあなたの人生の時間を節約することを願っています。そうでなければ、このタスクに費やされるでしょう!
二次元空間での線画
2次元および3次元空間での線描画シェーダーの私のエンジンでは、ほぼ同じコードが使用されます。 唯一の違いは、3次元の場合、線の3次元座標のスクリーンへの投影が追加され、同じアルゴリズムが追加されることです。
線に太さを与える一般的な方法があります-各線セグメントを長方形として表すため。 太線の最も単純な表現は次のようになります(図1) 。
(図1)
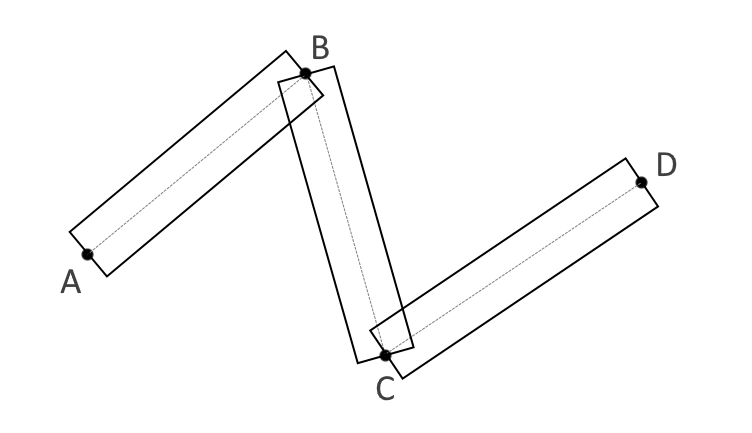
節点で目に見えるセグメンテーションを取り除くために、隣接セグメントの両方のセクションの厚さを保持するために、隣接セグメントの隣接ポイントを結合する必要があります。 これを行うには、線の片側の面の交差点を見つけます(図2) 。
(図2)
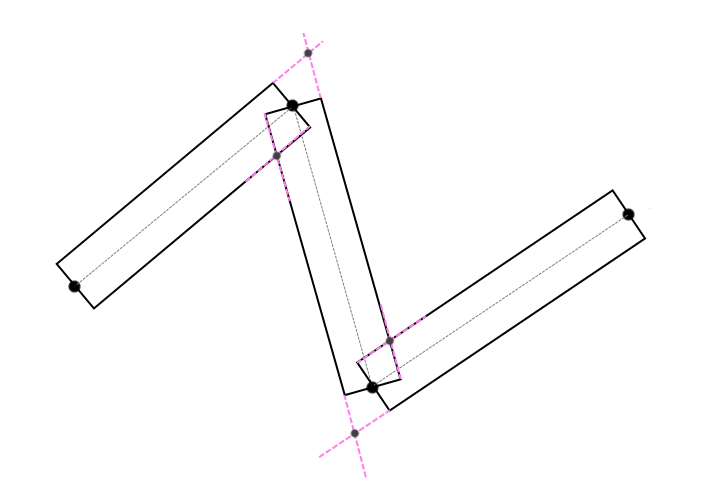
ただし、隣接するセグメント間の角度は非常に鋭いため、交差点はこれらの線の接続点から遠くなる可能性があります(図3) 。
(図3)
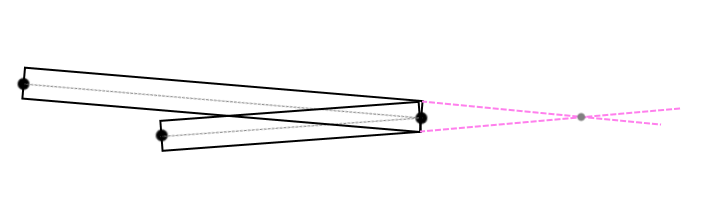
この場合、この角度は何らかの方法で処理する必要があります(図4) :
(図4)
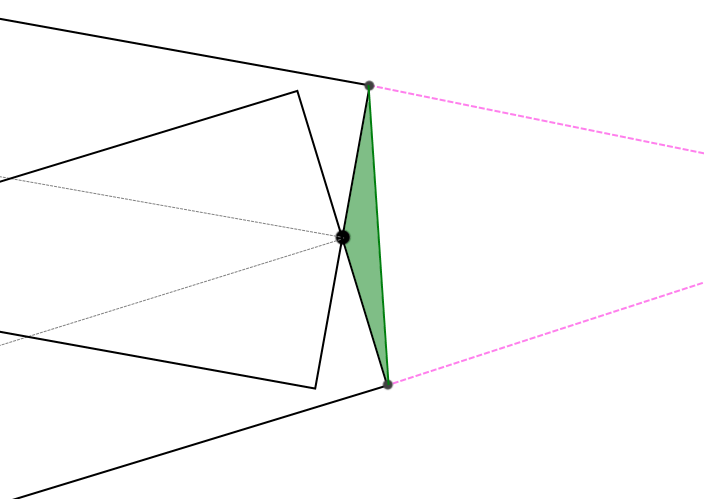
そのような領域に対応する三角形を塗りつぶすことにしました。 GL_LINE_STRINGシーケンスは私の助けになりました。正しい順序であれば、角度が鋭すぎる場合(頂点シェーダーでしきい値がチェックされます)、きちんとトリミングされたコーナーの効果を作成するか(図5) 、または片側の面を交差させる規則に従って隣接するセグメントの隣接座標を結合します(図。 。2)前と同じ。
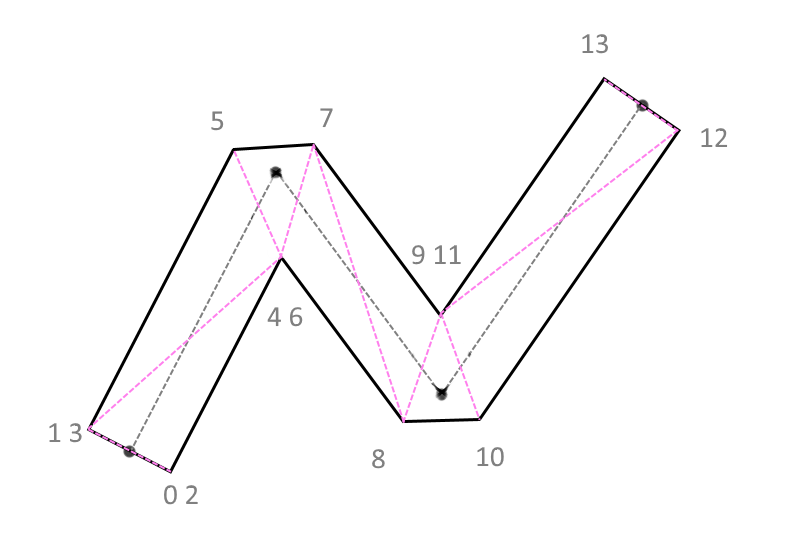
(図5)
頂点の近くの数字は、グラフィックスパイプラインでポリゴンを描画する頂点のインデックスです。 角度が鈍角の場合、この場合、トリミング用の三角形は無限に細い線にマージされ、見えなくなります(図6) 。
 (図6)
(図6)
このように自分自身へのシーケンスを想像します(図7) :

(図7)
それが完全な秘密です。 次に、これがどのようにレンダリングされるかを見てみましょう。 頂点バッファー、インデックスバッファー、順序バッファーを作成して、セグメントの現在の頂点からどの方向に太くするか、またセグメントのどの部分が現在頂点シェーダーによって処理されているかを初期または最終的に示す必要があります。 現在の点の座標に加えて、顔の交点を見つけるために、そこから前と次の座標を知る必要もあります(図8) 。
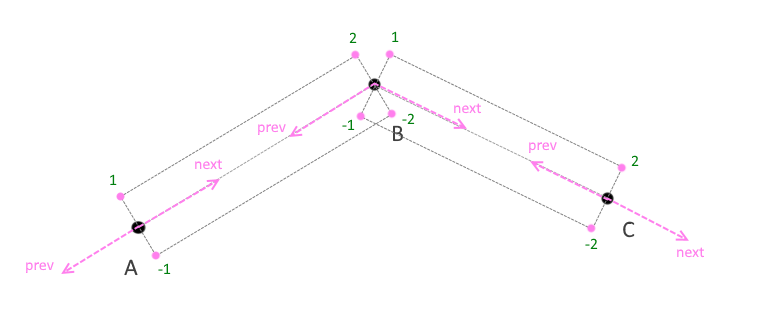
(図8)
したがって、シェーダーの各座標について、実際には座標自体、前の座標と次の座標、ポイントの順序、つまり ポイントがセグメントの開始点または終了点(-1、1が開始点、-2、2がセグメントの終了点)であるか、どのように配置するか:現在の座標の上または下、および太さと色。
なぜなら WebGLでは、さまざまな属性に1つのバッファーを使用できます。このバッファーの要素が座標である場合、 vertexAttribPointerが呼び出されると、各属性はバッファー要素のサイズと現在の属性要素に相対的なオフセットでバイト単位で割り当てられます。 これは、紙にシーケンスを描いた場合にはっきりと見られます(図9) 。
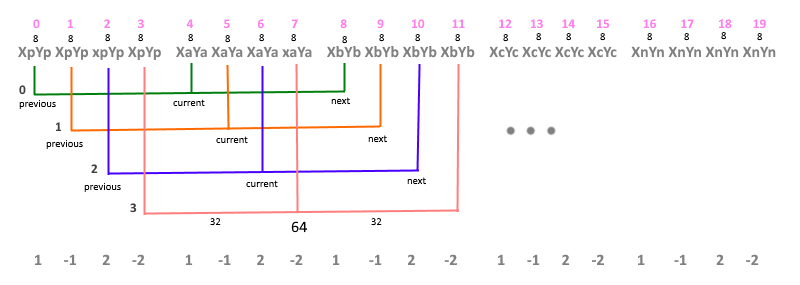
(写真9)
一番上の行は、頂点配列のインデックスです。 8-要素サイズ( 座標タイプvec2) 、つまり 2x4バイト。 Xi、Yi-ポイントA、B、Cの座標値。 Xp = Xa-Xb、Yp = Ya-Yb、Xn = Xc-Xb、Yn = Xc-Xbすなわち 境界点での方向を示すピーク。 色付きの円弧は、頂点シェーダーの各インデックスの座標バンドル(前、現在、次)を示します。 現在はリンクの現在の座標、 前はリンクの前の座標、 次はリンクの次の座標です。 値32バイトは、前の(前の)座標値に対する現在の(現在の)を識別するためのバッファー内のオフセットです。64バイトは、次の(次の)値を識別するためのバッファー内のオフセットです。 なぜなら 次の座標のインデックスは前の(前の)値で始まり、それに対する配列のオフセットはゼロです。 最後の行は、セグメント内の各座標の順序1と-1を示しています。これは、セグメントの始まりであり、それぞれ2と-2-セグメントの終わりです。
コードでは、次のようになります。
var vb = this._verticesBuffer; gl.bindBuffer(gl.ARRAY_BUFFER, vb); gl.vertexAttribPointer(sha.prev._pName, vb.itemSize, gl.FLOAT, false, 8, 0); gl.vertexAttribPointer(sha.current._pName, vb.itemSize, gl.FLOAT, false, 8, 32); gl.vertexAttribPointer(sha.next._pName, vb.itemSize, gl.FLOAT, false, 8, 64); gl.bindBuffer(gl.ARRAY_BUFFER, this._ordersBuffer); gl.vertexAttribPointer(sha.order._pName, this._ordersBuffer.itemSize, gl.FLOAT, false, 4, 0);
これは、頂点と順序の配列を作成する関数です。pathArrは 、配列を埋めてバッファを初期化する座標配列の配列です。outVerticesは座標の配列、 outOrdersは順序の配列、 outIndexesはインデックスの配列です。
Polyline2d.createLineData = function (pathArr, outVertices, outOrders, outIndexes) { var index = 0; outIndexes.push(0, 0); for ( var j = 0; j < pathArr.length; j++ ) { path = pathArr[j]; var startIndex = index; var last = [path[0][0] + path[0][0] - path[1][0], path[0][1] + path[0][1] - path[1][1]]; outVertices.push(last[0], last[1], last[0], last[1], last[0], last[1], last[0], last[1]); outOrders.push(1, -1, 2, -2); // 4 for ( var i = 0; i < path.length; i++ ) { var cur = path[i]; outVertices.push(cur[0], cur[1], cur[0], cur[1], cur[0], cur[1], cur[0], cur[1]); outOrders.push(1, -1, 2, -2); outIndexes.push(index++, index++, index++, index++); } var first = [path[path.length - 1][0] + path[path.length - 1][0] - path[path.length - 2][0], path[path.length - 1][1] + path[path.length - 1][1] - path[path.length - 2][1]]; outVertices.push(first[0], first[1], first[0], first[1], first[0], first[1], first[0], first[1]); outOrders.push(1, -1, 2, -2); outIndexes.push(index - 1, index - 1, index - 1, index - 1); if ( j < pathArr.length - 1 ) { index += 8; outIndexes.push(index, index); } } };
例:
var path = [[[-100, -50], [1, 2], [200, 15]]]; var vertices = [], orders = [], indexes = []; Polyline2d.createLineData(path, vertices, orders, indexes);
取得するもの:
頂点:[-201、-102、-201、-102、-201、-102、-201、-102、-100、-50、-100、-50、-100、-50、-100、-50 、1、2、1、2、1、2、1、2、200、15、200、15、200、15、200、15、399、28、399、28、399、28、399、28]
次数:[1、-1、2、-2、1、-1、2、-2、1、-1、2、-2、1、-1、2、-2、1、-1、2、 -2]
インデックス:[0、0、0、1、2、3、4、5、6、7、8、9、10、11、11、11、11、11]
頂点シェーダー:
attribute vec2 prev; // attribute vec2 current; // attribute vec2 next; // attribute float order; // uniform float thickness; // uniform vec2 viewport; // // vec2 proj(vec2 coordinates){ return coordinates / viewport; } void main() { vec2 _next = next; vec2 _prev = prev; // , if( prev == current ) { if( next == current ){ _next = current + vec2(1.0, 0.0); _prev = current - next; } else { _prev = current + normalize(current - next); } } if( next == current ) { _next = current + normalize(current - _prev); } vec2 sNext = _next, sCurrent = current, sPrev = _prev; // , vec2 dirNext = normalize(sNext - sCurrent); vec2 dirPrev = normalize(sPrev - sCurrent); float dotNP = dot(dirNext, dirPrev); // vec2 normalNext = normalize(vec2(-dirNext.y, dirNext.x)); vec2 normalPrev = normalize(vec2(dirPrev.y, -dirPrev.x)); float d = thickness * 0.5 * sign(order); vec2 m; //m - , if( dotNP >= 0.99991 ) { m = sCurrent - normalPrev * d; } else { vec2 dir = normalPrev + normalNext; // (. 2) m = sCurrent + dir * d / (dirNext.x * dir.y - dirNext.y * dir.x); // if( dotNP > 0.5 && dot(dirNext + dirPrev, m - sCurrent) < 0.0 ) { float occw = order * sign(dirNext.x * dirPrev.y - dirNext.y * dirPrev.x); // LINE_STRING if( occw == -1.0 ) { m = sCurrent + normalPrev * d; } else if ( occw == 1.0 ) { m = sCurrent + normalNext * d; } else if ( occw == -2.0 ) { m = sCurrent + normalNext * d; } else if ( occw == 2.0 ) { m = sCurrent + normalPrev * d; } // "" , } else if ( distance(sCurrent, m) > min(distance(sCurrent, sNext), distance(sCurrent, sPrev)) ) { m = sCurrent + normalNext * d; } } m = proj(m); gl_Position = vec4(mx, my, 0.0, 1.0); }
結論にいくつかの言葉
このアプローチは、トラック、軌道 、 ベクターデータを描画するために実装されています 。
結論として、アルゴリズムを使用して行の品質を向上させる方法についていくつかのアイデアを追加します。 たとえば、各頂点のカラー属性に色を渡すと、線はマルチカラーになります。 また、各頂点に幅を送信すると、ラインの幅がポイントからポイントに変更され、観測ポイントからの距離に関連するポイントの頂点シェーダーで計算すると( 3次元の場合) 、ラインの一部が配置されたときに効果を得ることができます遠くにある線の部分より視覚的に大きい観測点に近い。 また、太い線の各エッジに2つのパスを追加してアンチエイリアスを実装することもできます。この場合、中央部分に対してわずかな透明度で細い線(エッジの周りのフレーム)が描画されます。