ネットワークからの写真は、品質がより良いことを望みますが、数字を視覚化する際の経験の本質を正確に反映しています。 根を見ることは、世代の知恵の基盤です。
ちょっとした歴史
学校に戻って、物理学の授業で、私はオシロスコープを覗きました。画面には、互いに変化し、さまざまな数字が現れました：最初の単純なもの-直線、放物線、円、楕円 このレースの歌姫の作者は、フランスの物理学者であり、パリ科学アカデミー（1879）のメンバーであるジュール・アントワーヌ・リサジューでした[1]。 図形自体は、互いに垂直な2つの方向に2つの調和振動を同時に実行する点によって描かれた閉じた軌道です[2]。 現代から遠く離れた時代において、ジュールの主なメリットは、確かに経験によって蓄積された数学と物理学の知識に加えて、即興の手段によるこれらの数字の単純な機械的視覚化だったと思います。 ジュールのようにできるだけシンプルかつ視覚的に構築して、線形測定の現代の課題に関連した彼のアイデアを実現したかったのです。 しかし、Pythonで結果をグラフィカルに視覚化した数学的モデリングによってこれを行うには。 しかし、最初に、図の構成の古典的なバージョン[3]を検討してください。
リサジューの数字はどうあるべきか
これを行うには、図を記述する方程式系を使用します。
一般的な場合のx（t）、y（t）、相互に垂直な平面に沿った時間依存の調和振動、周波数b、a、および初期位相d。 計算で数値を分析するには、周波数差のモジュラス| b-a | = 1.円形周波数b / aと初期位相dの比を考慮します。 線A = B d = 0、円について
、および放物線 
。 条件を満たした主要な周波数関係をネストされたリストに入力しますm = [[0]、[2.2]、[2.1]、[1,2]、[3,2]、[3,4]、[5 、4]、[5,6]、[9,8]]。
各図を別々のチャートにプロットするためのコード
#!/usr/bin/env python #coding=utf8 import numpy as np from numpy import sin,pi import matplotlib.pyplot as plt m=[[0],[2,2],[2,1],[1,2],[3,2],[3,4],[5,4],[5,6],[9,8]]# for i in m: if i[0]==0: a=1 x=[sin(a*t) for t in np.arange(0.,2*pi,0.01)] y=[sin(a*t) for t in np.arange(0.,2*pi,0.01)] plt.plot(x, y, 'r')# plt.grid(True) plt.show() else: a=i[0] b=i[1] d=0.5*pi x=[sin(a*t+d) for t in np.arange(0.,2*pi,0.01)] y=[sin(b*t) for t in np.arange(0.,2*pi,0.01)] plt.plot(x, y, 'r') # a/b # plt.grid (True) plt.show()
私は結果を出しません、個々の数字は印象的ではありません。 「レース」のコラージュが欲しい。
m = [3,4]、[5,4]、[5,6]、[9,8]]の4つの図の1つのフォームグラフにプロットするためのプログラムコード
#!/usr/bin/env python #coding=utf8 import numpy as np from numpy import sin,pi import matplotlib.pyplot as plt m=[[3,4],[5,4],[5,6],[9,8]] # plt.figure(1) for i in m: a=i[0] b=i[1] d=0.5*pi x=[sin(a*t+d) for t in np.arange(0.,2*pi,0.01)] y=[sin(b*t) for t in np.arange(0.,2*pi,0.01)] if m.index(i)==0: plt.subplot(221) plt.plot(x, y, 'k') # a/b plt.grid(True) elif m.index(i)==1: plt.subplot(222) plt.plot(x, y, 'g') plt.grid(True) elif m.index(i)==2: plt.subplot(223) plt.plot(x, y, 'b') plt.grid(True) else: plt.subplot(224) plt.plot(x, y, 'r') plt.grid(True ) plt.show()
そして、ここで彼らは「レース」です。
それらの孤立の定義によってリサージュの数字に帰せられないもの
なぜ必要なのか| b-a | = 1、“ for the flags！”たとえば、m = [[1,3]、[1,5]、[1,7]、[1,9]]を試してみましょう
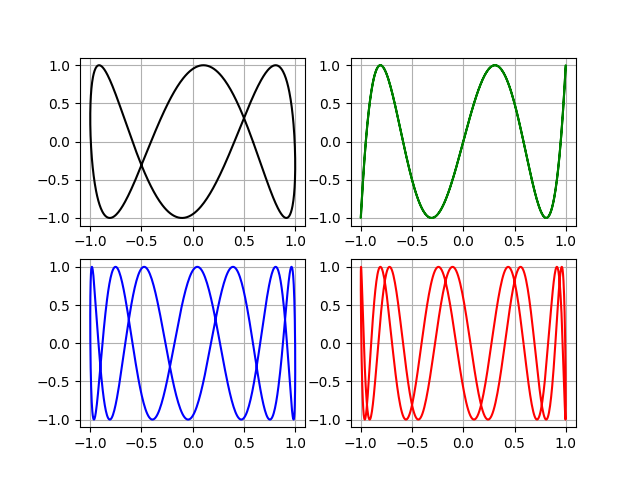
2番目のグラフでは、m = 0.2の場合、開いた軌道が取得されますが、これは定義上、Lbssazhuの図ではありません。
機械的アナログを探して
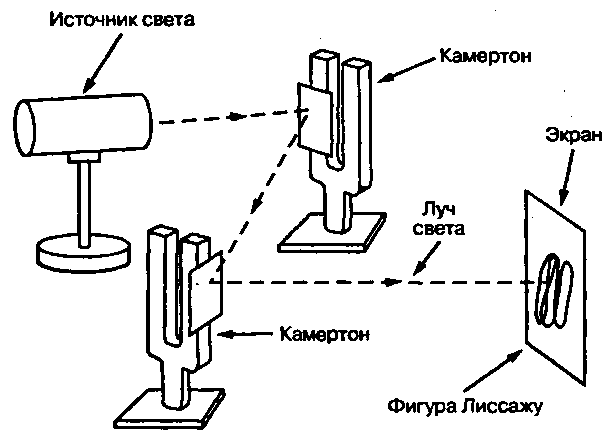
測定技術の図の類似点を探してみましょう。これは、楕円管の形の共振器を備えた振動レベルゲージです[4]。
自励システム5,6,7を使用した楕円断面の弾性的に固定されたチューブは、1つの平面で自励振動を行い、システム8、9、10の助けを借りて、最初の平面に垂直な別の平面で自励振動します。 チューブは、互いに近い周波数の異なる2つの相互に垂直な平面で振動します。 チューブの質量は、チューブを満たす液体のレベルに依存します。 質量が変化すると、チューブの振動周波数も変化します。これは、レベルゲージの出力信号です。 周波数は、周波数がマイクロプロセッサ11によって処理されるときに補償される乗法および加法追加誤差に関する追加情報を運びます。
適切なモデリングの条件
多かれ少なかれ、リサージュの数値を前述のレベルゲージの動作に正しくリンクするには、次の状況を考慮する必要があります。 まず、一方の端に固定された楕円管は、分布パラメーターを備えた振動システムであり、その振動の分析を非常に複雑にします。 第二に、管の振動周波数の比は任意に変えることができません;それは断面の楕円と振動励起システムの許容ギャップに依存します。 周波数比については、単純な比を取得できます。
変数が属するもの、a、b、a0、b0は図から明らかであり、さらに、発振器の周期周波数の式は学校の物理学コースで知られています。 「Pythonでの実装では、最後の関係で、チューブの内側セクションの壁の厚さと楕円インデックスを導入し、4つの変数の代わりに3つを取得します。
決定するプログラムコード。 周波数比の許容される変化
#!/usr/bin/env python #coding=utf8 import numpy as np from numpy import sqrt import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' d=0.5 a=9 x=[w for w in np.linspace(0.8,0.95,15)] y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)] plt.plot(x, y, 'r', label=' . -- %s' %str(d)) d=0.7 y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)] plt.plot(x, y, 'b',label=' .-- %s' %str(d)) d=1.0 y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)] plt.plot(x, y, 'g', label=' .-- %s' %str(d)) plt.ylabel(' ') plt.xlabel(' ') plt.title(' ') plt.legend(loc='best') plt.grid(True) plt.show()
プログラムの結果、スケジュールを取得します。
グラフは、9 mmの小さな内部軸用に作成されています。 0.8〜0.95の範囲のセクションの小さい半軸と大きい半軸の建設的に許容される比率の場合。 これは、周波数比に影響を与える主な要因であり、1.18から1.04まで変化します。 壁の厚さはわずかに影響します。 これでさまざまな関係が得られ、さらなるモデリングに使用できます。
チューブの垂直軸の波形
カンチレバーチューブの分散された機械的パラメータについては、固有周波数とインピーダンスの等価性を使用して、剛性と減衰の集中質量に減らすことができます。 さらに、カンチレバーチューブの曲げ振動の形態を決定するために、分布パラメータの式を取得できます。 フォームの方程式-ビーム関数の形式は次のとおりです。
どこで
-方程式の根：
カンチレバーのロッド、ビーム、またはチューブの振動の形式と周波数に関する多数の出版物にもかかわらず、式（4）はどこにも与えられておらず、座標のない数字のみが与えられていることに注意すべきです。 したがって、端部の条件とビーム関数を使用して式（4）を推定し、根（5）とノードの位置を確認しました。 ただし、これは簡単に忘れられる些細な方程式です。
式1.1の根を数値的に決定し、チューブ軸の3つの形式の曲げ振動を構築するためのプログラムコード
1.1-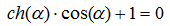 
#!/usr/bin/env python #coding=utf8 from scipy.optimize import * import numpy as np from numpy import pi,cos,cosh,sin,sinh import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' d=[] for i in range(0,4): x=brentq(lambda x:cosh(x)*cos(x)+1,0+pi*i,pi+pi*i) p=round(x,3) if p not in d: d.append(p) x=[w for w in np.linspace(0,1,100)] k=d[0] z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x) )for x in np.linspace(0,1,100)] plt.plot(z, x, 'g', label=' - %s' %str(k)) k=d[1] z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x)) for x in np.linspace(0,1,100)] plt.plot(z, x, 'b', label=' - %s' %str(k)) k=d[2] z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x)) for x in np.linspace(0,1,100)] plt.plot(z, x, 'r', label=' - %s' %str(k)) plt.title(' ') plt.xlabel(' OX ') plt.ylabel(' OZ ') plt.legend(loc='best') plt.grid(True) plt.show()
プログラムの結果として、チューブの垂直位置を考慮に入れたグラフが作成されます。
グラフでは、軸線の座標がチューブの長さに縮小され、振幅が正規化されます。 取り付け位置に対するチューブの振動ノードの位置は、振動の理論に正確に対応しています。
チューブはどの経路で終わりますか
最後の障害は、いくつかのパラメーターが同時に変化する場合、振動の微分方程式の意味のある数値解を得ることの難しさです。 ここで、Python [5,6]の振動リンクに関する私の記事の2つが助けになりました。そこでは、微分方程式の正確なシンボリックな解を得るためのテクニックが与えられています。
周波数aとbが異なるOX平面とOY平面の管振動について、2つの条件付き独立方程式を書きます。これらの関係は、以前に確立された範囲から選択されます。 残りのパラメーターは正しい関係で選択されますが、結果をより適切に示すために任意に選択されます。
ここでは、次の表記法を紹介します（インデックスなしで単純化するため）。
─力の振幅の減少、 
─減衰係数、 
─システムの振動の固有振動数、m─集中質量は両方の方程式で同じであり、 
─振幅が異なるために減衰係数が異なるため、振動励起システムのギャップが異なるため、 
─チューブセクションの楕円率による異なる剛性。
システム（6）の各微分方程式を解くためのプログラムコード。その後に追加して、チューブの端の軌跡を取得します。
import numpy as np from sympy import * from IPython.display import * import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' def solution(w,v,i,n1,n2,B,f,N): t=Symbol('t') var('t C1 C2') u = Function("u")(t) de = Eq(u.diff(t, t) +2*B*u.diff(t) +w**2* u, f*sin(w*t+v)) des = dsolve(de,u) eq1=des.rhs.subs(t,0) eq2=des.rhs.diff(t).subs(t,0) seq=solve([eq1,eq2],C1,C2) rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])]) g= lambdify(t, rez, "numpy") t= np.linspace(n1,n2,N) plt.figure(1) if i==1: plt.subplot(221) plt.plot(t,g(t),color='b', linewidth=3,label='x=%s*sin(%s*t+%s)' %(str(f),str(w),str(v))) plt.legend(loc='best') plt.grid(True) else: plt.subplot(222) plt.plot(t,g(t),color='g', linewidth=3,label='y=%s*sin(%s*t+%s)' %(str(f),str(w),str(v))) plt.legend(loc='best') plt.plot(t,g(t),color='r', linewidth=3) plt.grid(True) return g(t) N=1000# B=0.2# f=1# n1=0# n2=20# w1=5.0# w2=10.0# v1=0# v2=0# g1=solution(w1,v1,1,n1,n2,B,f,N) g2=solution(w2,v2,2,n1,n2,B,f,N) plt.subplot(223) plt.plot(g1,g2,color='b', linewidth=3,label='w1/w2=%s'%str(w1/w2)) plt.legend(loc='best') plt.grid(True) plt.subplot(224) x=[w for w in np.linspace(0,1,100)] k=1.875 z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x) )for x in np.linspace(0,1,100)] plt.plot(z, x, 'g',label=' -%s'%str(k)) plt.legend(loc='best') plt.grid(True) plt.show()
このプログラムを使用すると、モデルのすべてのパラメーターを変更できます。たとえば、次の場合です。
N = 1000、B = 0.2、f = 1、n1 = 0、n2 = 20、w1 = 5.0、w2 = 10.0、v1 = 0、v2 = 0
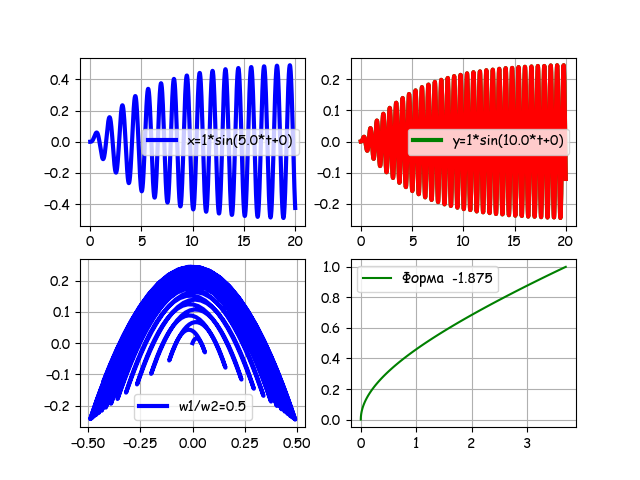
周波数比が0.5の場合、過渡は形状を乗算します。 時間n15 = 0、n2 = 20の「ゲート」を入力します。
「ゲート」を削除し、初期フェーズv2 = -pi / 2を入力すると、次のようになります。
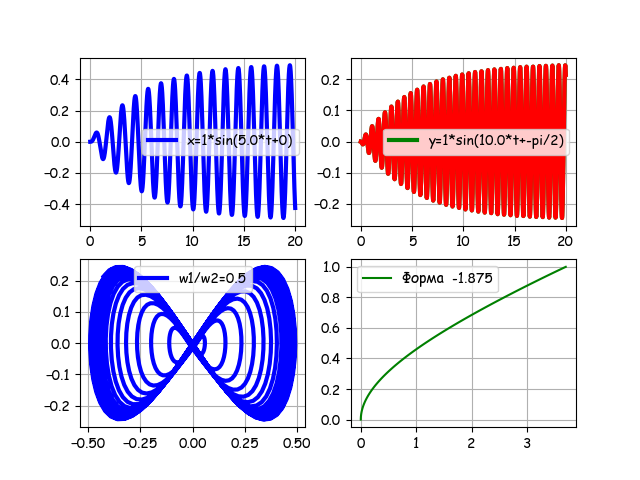
前述の観点から、グラフィックスについての解説は必要ありません。
陰謀のために
この記事で読者を見つけた場合、または読者が過去の影を恐れずに見つけた場合、その中の充填液のレベルが変化したときのチューブの複雑な空間振動の3次元アニメーショングラフィックスを公開します。
結論の代わりに
ジュール・アントワーヌ・リサジューの発明は彼の旅を時間的に続けますが、すでにPythonにいます。 提示された解釈が、もちろん完璧とはほど遠いものであり、私たちが独創的な数学者リサジューの作品と知り合いを続けられることを願っています。