この記事では、数学的形態学を使用した画像フィルタリングへの注目に値するアプローチの1つを検討したいと思います。 数学的形態について多くの記事が書かれており、そのうちの1つがハブに投稿されています。 このトピックに不慣れな読者のために、上記のリンクの資料を最初に読むことをお勧めします。
画像フィルタリングに関する記事で、メディアンフィルターを使用したフィルタリングの方法について説明しました。 このフィルターは非常に優れていることが判明しましたが、いくつかの制限と不便さがあります。
3x3の実装でもかさばる:
- ウィンドウ関数の形成が必要です
- ウィンドウを拡大するのは非常に難しい
- 他のウィンドウ機能と直列に接続した場合、大きな遅延。
これらの不便さはすべて、デジタル画像処理システムへの適用性を損なうものではありませんが、別のアプローチがあります。
数学的形態を使用して画像をフィルタリングすることは、長い間よく知られているトピックであり、読者に紹介するのに少し近づいたいだけです。
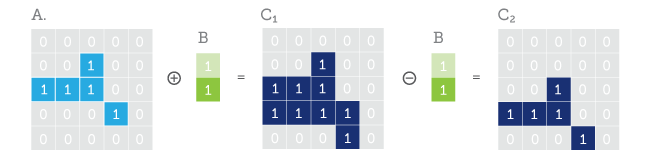
上記の記事からすでに見たように、基本的な形態学的操作、 縮小(侵食)および拡大(膨張)から 、 開閉操作を構築できます。
オープン操作は、 侵食->拡張の順次実行です。 このような組み合わせは、単一ピクセルとその小さなクラスターが縮小によって取り消せないほど消費されるという事実につながり、また大きなオブジェクトが両側でかじられます)。 大きなオブジェクト内に小さな穴がある場合、それらは大きくなります。 その後の拡張操作により、かじったオブジェクトが元のサイズに復元されますが、狭くなることで小さな破片が消費されることはなくなります。
クローズ操作は、 膨張→収縮の順次実行です。 この操作は、最初にオブジェクト内の穴を埋めて少し厚くし、次に元の厚さに減らしますが、穴はもうありません。
開閉操作の連続実行は非常に優れたフィルターであり、中央値より悪くはありませんが、逆にオブジェクトの漏れを少なくします。 前提条件は、基本操作の同じウィンドウサイズです。
ただし、基本的な収縮操作または膨張操作はそれぞれ同じウィンドウ関数であり、3x3ウィンドウを実装するには少なくとも2つのFIFOが必要であり、関数に応じて論理ANDまたはOR操作が必要です。
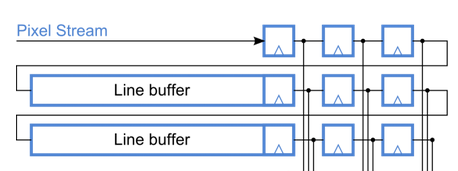
より深いフィルタリングには、5x5および7x7ウィンドウがよく使用されます。これは、FIFOエレメントのメモリ量と合計遅延時間の増加を伴います。
アルテラのFPGAにこのような操作を実装するには、FIFOメガファンクションと内蔵2ポートメモリを使用できますが、そのようなFIFOは1ビット幅であり、2値化された画像にはこれ以上必要ありません。M4Kなどのメモリブロック全体が必要です。また、あまり経済的ではありません。
低複雑度法
代替ソリューションを探している間、私はいわゆる低複雑度の方法でネットワークを偶然見つけました。 このメソッドの本質は、ウィンドウ関数の行列の分解です。 元の行列は2つに分解されます。
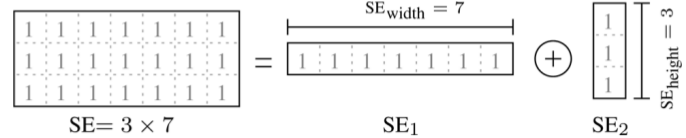
そして、それはこの画像に従って動作します:
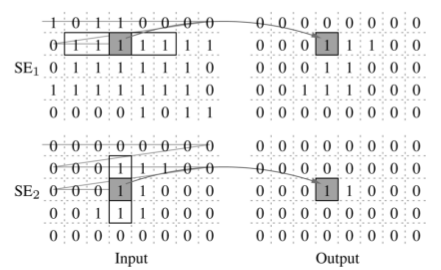
残念なことに、私は数学が苦手で、大学でマトリックス分解のトピックを経験しましたが、それは過ぎ去りました。 したがって、数学的な観点からそれがどのように機能するのか、なぜそうなのかを伝えるために、そうでない場合は明らかにしません。
上記の記事では、低複雑度法を使用した収縮操作と膨張操作の実装の機能図を示しました。 このスキームは2つのブロックで構成され、各ブロックは構造要素SE1およびSE2を表します。

この図から、浸食/膨張操作の選択は、入力データを反転することによって実行されることが明らかです。 これらの操作は対称的です。
Stage-1ブロックの出力は、入力ピクセルの値とffトリガーの累積量に依存します。 この量が構造要素SE1のウィンドウの幅と等しくなるとすぐに、ブロックの出力は「1」になり、そうでない場合は「0」になります。 ブロックの入力の「0」は、トリガーffの累積量をゼロにリセットします。 明らかに、このブロックは構造要素SE1の下の連続するユニットの数をカウントします。
Stage-1ユニットの出力は、 Stage-2ユニットの入力に送られ、同じ原理で動作します。 Stage-1ブロックとの違いは、入力イメージの列数の深さを持つRow_memメモリの使用であり、合計はこのメモリの列ごとに個別に保存されます。 列の合計が構造要素SE2の高さと等しい場合のみ、ブロック「1」の出力。 Stage-2の出力は、実行された収縮または膨張操作に応じて反転できます。
したがって、 Stage-1ブロックでは、回路は水平要素SE1の下のすべての「1」を監視し、結果をStage2ブロックに転送します。Stage -2ブロックは、 SE1の出力を考慮して、垂直要素SE2の下のすべての「1」を監視します。
また、このスキームでは、画像の境界で構造要素SEの動作を保証する信号が提供されます。

画像の境界は、通常、主要なポイントの名前で示されます:北、南、西、東。 構造要素SEが画像の境界にある場合、構造要素のサイズの半分に対応する必要な数のユニットまたはゼロの挿入( パディング )が提供されます。
この方法の大きな利点は、メモリの節約です。 Stage-1およびStage-2ブロックに必要なメモリの量は、次と等しいワードサイズ( WL )によって決まります。
Log2(SE1_width)およびLog2(SE2_height) Stage-2ブロックでは、トリガーは使用されませんが、 Row_memメモリのボリュームはImage_width x Log2(SE2_height)です。
明らかに、対数の計算結果は、最も近いビット深度値SE1_widthおよびSE2_heightに丸める必要があります。 ウィンドウが3x5の場合、丸められた値はLog2(SE1_width)= 2ビット 、 Log2(SE2_height)= 3ビットです。
低複雑度方式と通常のウィンドウ方式では、3x3ウィンドウのメモリ使用量に違いがないことに気付くのは難しくありません。 最初のケースでは、メモリの量は320列x 2ビットであり、2番目のケースでは、サイズが320要素の2つの1ビットFIFO要素です。 ウィンドウサイズが5x5または7x7に変更された場合、FIFOの数はウィンドウの行数に比例して増加しますが、メソッドの複雑さが低いため、ワードサイズは1ビットだけ増加し、Row_memメモリは320x2ではなく320x3になります。
したがって、最大ウィンドウサイズを事前設定して、たとえば、このサイズのメガファンクションaltsyncramを使用できます。 これは、FIFOを使用してウィンドウ関数を形成するよりもはるかに経済的です。
Verilog収縮/膨張モジュールコード:
低複雑度の侵食/膨張
module low_complexity #(parameter BW = 3'd3, parameter BH = 3'd3, parameter WIDTH = 9'd320, parameter HEIGH = 9'd240, parameter START_X = 9'd320, parameter START_Y = 9'h0 ) ( input wire clk, input wire er_dil, input wire [0:0] data_in, input wire input_valid, input wire [10:0] x_in, y_in, output wire output_valid, output wire [0:0] data_out ); localparam END_X = (WIDTH + START_X) - 1; localparam END_Y = HEIGH - 1; wire e_bound, s_bound, n_bound, w_bound; assign n_bound = (y_in == START_Y && x_in == START_X) ? 1'b1 : 1'b0; assign s_bound = (y_in == END_Y && x_in == END_X) ? 1'b1 : 1'b0; assign w_bound = (x_in == START_X) ? 1'b1 : 1'b0; assign e_bound = (x_in == END_X) ? 1'b1 : 1'b0; // stage 1 wire mux1_out, mux2_out; wire [2:0] mux3_out; wire [2:0] mux4_out; reg [2:0] ff = 0; reg [2:0] ff_d = 0; wire [2:0] sum1; wire [2:0] mux5_out; wire cmp1_out; wire [8:0] mem_addr = input_valid ? x_in[8:0] - START_X : 9'd0; assign mux1_out = er_dil ? ~data_in : data_in; assign mux2_out = (e_bound | s_bound) ? 1'b1 : mux1_out; assign mux3_out = mux2_out ? sum1 : 3'h0; assign mux4_out = cmp1_out ? mux5_out : mux3_out; always @(posedge clk) ff_d = mux4_out; always @* ff = ff_d; assign mux5_out = w_bound ? BH - 1'b1 : ff; assign sum1 = mux5_out + 1'b1; assign cmp1_out = (mux3_out == BW) ? 1'b1 : 1'b0; // stage2 2 wire [2:0] sum2; wire [2:0] mux6_out, mux7_out; wire cmp2_out; wire [2:0] mux8_out; wire [2:0] mem_out; alt_ram320x3 row_mem ( .clock(clk), .data(mux7_out), .rdaddress(mem_addr), .wraddress(mem_addr), .wren(1'b1), .q(mem_out) ); assign mux6_out = cmp1_out ? sum2 : 3'h0; assign mux7_out = cmp2_out ? mux8_out : mux6_out; assign mux8_out = n_bound ? BW : mem_out; assign sum2 = mux8_out + 1'b1; assign cmp2_out = (mux6_out == BH) ? 1'b1 : 1'b0; assign data_out = er_dil ? ~cmp2_out : cmp2_out; assign output_valid = input_valid; endmodule
開閉操作:
開閉
wire [0:0] er1_out, dil1_out, er2_out, dil2_out; wire dil_input = line_data_out; // OPENING // EROSION 3x3 low_complexity #( .BW(3'h3), .BH(3'h3), .WIDTH(9'd320), .HEIGH(9'd240), .START_X(9'd320), .START_Y(9'h0) ) er_1 ( .clk(clk), .er_dil(1'b0), .data_in(dil_input), .input_valid(line_rd_rq), .x_in(x_in), .y_in(y_in), .output_valid(), .data_out(er1_out) ); // DILATION 3x3 low_complexity #( .BW(3'h3), .BH(3'h3), .WIDTH(9'd320), .HEIGH(9'd240), .START_X(9'd320), .START_Y(9'h0) ) dil_1 ( .clk(clk), .er_dil(1'b1), .data_in(er1_out), .input_valid(line_rd_rq), .x_in(x_in), .y_in(y_in), .output_valid(), .data_out(dil1_out) ); // CLOSING // DILATION 3x3 low_complexity #( .BW(3'h3), .BH(3'h3), .WIDTH(9'd320), .HEIGH(9'd240), .START_X(9'd320), .START_Y(9'h0) ) dil_2 ( .clk(clk), .er_dil(1'b1), .data_in(dil1_out), .input_valid(line_rd_rq), .x_in(x_in), .y_in(y_in), .output_valid(), .data_out(dil2_out) ); // EROSION 3x3 low_complexity #( .BW(3'h3), .BH(3'h3), .WIDTH(9'd320), .HEIGH(9'd240), .START_X(9'd320), .START_Y(9'h0) ) er_2 ( .clk(clk), .er_dil(1'b0), .data_in(dil2_out), .input_valid(line_rd_rq), .x_in(x_in), .y_in(y_in), .output_valid(), .data_out(er2_out) );
結果
このビデオは、同じサイズのウィンドウを持つメディアンフィルターと比較して、3x3ウィンドウを持つ低複雑度法を使用した画像フィルタリングの効果を示しています。
緑色のマーカー-中央値フィルター
黄色のマーカー-形態
フィルター処理されていないゴミは緑のマーカーでビデオに表示され、検出器はそれをフレームに入れ、黄色のマーカーでビデオではゴミが消えて大きなオブジェクトのみがフレームに入ります。
この実験から、数学的モルフォロジーに基づくフィルターは中央値よりも若干優れていると結論付けることができます。
結論
低複雑度の侵食/膨張法に基づいて、ウィンドウ関数を形成するよりも、メモリ消費の観点から、モルフォロジー画像処理の基本要素をはるかに効率的に構築できます。
数学的形態学を使用して画像をフィルタリングした結果は、メディアンフィルターでフィルタリングした結果よりも悪くはなく、メディアンフィルターの優れた代替手段です。
関連資料
→ 低複雑度法
→ 形態学的画像処理
→ 数学的形態