 こんにちは同僚。 Moustache and Claws社での典型的なオンライン実験を考えてみましょう。 彼女は、角の丸い長方形の赤いボタンがあるWebサイトを持っています。 ユーザーがこのボタンをクリックすると、世界のどこかで子猫がうれしくなります。 会社の目標は、ゴロゴロを最大限にすることです。 ボタンの形状と、それがインプレッションからクリック音への変換にどのように影響するかを熱心に調査するマーケティング部門もあります。 同社の予算のほぼすべてを独自の研究に費やしたため、マーケティング部門は4つの派warに分かれました。 各グループには、ボタンがどのように見えるかについての独創的なアイデアがあります。 一般に、ボタンの形状に反対する人はいませんが、赤色はすべてのマーケティング担当者を困らせ、最終的に、4つの代替オプションが提案されました。 実際、どのようなオプションであるかはそれほど重要ではありません。 マーケティングはA / B / nテストの実施を申し出ていますが、私たちは同意しません。したがって、これらの疑わしい研究にお金が投資されています。 できるだけ多くの子猫を幸せにし、交通量を節約してみましょう。 テストに許可されるトラフィックを最適化するために、ベイジアンの多腕バンディットのギャングを使用します。 進む。
こんにちは同僚。 Moustache and Claws社での典型的なオンライン実験を考えてみましょう。 彼女は、角の丸い長方形の赤いボタンがあるWebサイトを持っています。 ユーザーがこのボタンをクリックすると、世界のどこかで子猫がうれしくなります。 会社の目標は、ゴロゴロを最大限にすることです。 ボタンの形状と、それがインプレッションからクリック音への変換にどのように影響するかを熱心に調査するマーケティング部門もあります。 同社の予算のほぼすべてを独自の研究に費やしたため、マーケティング部門は4つの派warに分かれました。 各グループには、ボタンがどのように見えるかについての独創的なアイデアがあります。 一般に、ボタンの形状に反対する人はいませんが、赤色はすべてのマーケティング担当者を困らせ、最終的に、4つの代替オプションが提案されました。 実際、どのようなオプションであるかはそれほど重要ではありません。 マーケティングはA / B / nテストの実施を申し出ていますが、私たちは同意しません。したがって、これらの疑わしい研究にお金が投資されています。 できるだけ多くの子猫を幸せにし、交通量を節約してみましょう。 テストに許可されるトラフィックを最適化するために、ベイジアンの多腕バンディットのギャングを使用します。 進む。
A / B / nテスト
クリックはランダム変数であると仮定します 値をとる または 確率で そして それに応じて。 この数量には、パラメーターを持つベルヌーイ分布があります :
ベルヌーイ分布の平均値は 、分散は 。
最初に、通常のA / B / n検定を使用して問題を解決してみましょう。ここで、nは2つの仮説ではなく、いくつかの仮説が検定されることを意味します。 私たちの場合、これらは5つの仮説です。 ただし、最初に古いソリューションを新しいソリューションに対してテストする状況を検討してから、5つのケースすべてに一般化しています。 バイナリの場合、2つの仮説があります。
- 帰無仮説 古いボタンをクリックする確率に違いがないという事実にあります または新しい ;
- 対立仮説 古いボタンをクリックする確率が 新品より少ない ;
- 確率 そして コントロールグループと実験/テストグループ(処理)でのクリックとインプレッションの比率をそれぞれ推定します。
コンバージョンの真価を知ることはできません 現在のボタンのバリエーション(赤)についてですが、評価することができます。 このために、連携する2つのメカニズムがあります。 まず、これは大きな数の法則であり、ランダム変数の分布が何であれ、十分な数のサンプルと平均をサンプリングすると、この推定値は平均分布値の真の値に近くなります(ここではインデックスを省略します) 明確にするために):
第二に、これは中心極限定理であり、次のことを述べています:独立した同一分布のランダム変数の無限級数があると仮定します 、真の期待を込めて および分散 。 最終的な金額は それから
または同等に、十分に大きいサンプルの場合、平均値の推定値は、 および分散 :
どうやらそれを取り、2つのテストを実行します。トラフィックを2つの部分に分け、数日待ってから、最初のメカニズムでクリックの平均値を比較します。 2番目のメカニズムでは、 t検定を使用して、サンプルの平均値の差の統計的有意性を評価できます(平均推定値には正規分布があるため)。 サンプルサイズを増やすだけでなく 、平均スコアの分散を減らして、信頼性を高めます。 しかし、1つの重要な質問が残っています。各ボタンのバリエーションにどれだけのトラフィック(ユーザー)を乗せるか? 統計によれば、差がゼロでない場合、値が等しくないという意味ではありません。 たぶん運が悪くて、最初の ユーザーはある色をひどく嫌っていたので、別の色を待つ必要があります。 そして、違いがある場合にそれが重要であることを確認するために、ボタンの各バリエーションに使用するユーザーの数が問題になります。 これを行うには、マーケティング部門と再度会っていくつかの質問をする必要があります。おそらく、第1種と第2種のエラーとは何かを説明する必要があります。 一般的に、これはテスト全体で最も困難な場合があります。 それでは、これらのミスの種類を思い出し、バリエーションごとのトラフィック量を推定するためにマーケティング部門が尋ねるべき質問を決定しましょう。 最終的には、どのボタンの色を残すかを最終的に決定するのはマーケティングです。
| 真の仮説 | |||
| テスト回答 | 受け入れた | 誤って受け入れられた
(II種のエラー) | |
| 間違って拒否されました
(第一種のエラー) | 拒否されました | ||
さらにいくつかの概念を紹介します。 第一種のエラーの確率を 、つまり 帰無仮説が実際に真であるという条件で、対立仮説を採用する確率。 この値は統計的有意性と呼ばれます。 また、第2種のエラーの確率を導入する必要があります 。 価値 統計的検出力と呼ばれます。
統計的有意性と検出力の意味を説明するために、以下の画像を検討してください。 制御グループ内のランダム変数の平均分布が 、テスト中 。 いくつかの重要なしきい値を選択します 拒否されました(垂直の緑色の線)。 次に、値がしきい値の右側にあるが、コントロールグループの分布からのものである場合、誤ってテストグループの分布に起因するものとします。 それは第一種の間違いであり、価値 領域は赤で網掛けされています。 したがって、青色で網掛けされた領域の面積は 。 価値 実際、統計的検出力と呼ばれる、対立仮説に実際に帰属する対立仮説に対応する値の数を示しています。 上記を説明します。
# mu_c = 0.1 mu_t = 0.6 # s_c = 0.25 s_t = 0.3 # : , # c = 1.3*(mu_c + mu_t)/2
support = np.linspace( stats.norm.ppf(0.0001, loc=mu_c, scale=s_c), stats.norm.ppf(1 - 0.0005, loc=mu_t, scale=s_t), 1000) y1 = stats.norm.pdf(support, loc=mu_c, scale=s_c) y2 = stats.norm.pdf(support, loc=mu_t, scale=s_t) fig, ax = plt.subplots() ax.plot(support, y1, color='r', label='y1: control') ax.plot(support, y2, color='b', label='y2: treatment') ax.set_ylim(0, 1.1*np.max([ stats.norm.pdf(mu_c, loc=mu_c, scale=s_c), stats.norm.pdf(mu_t, loc=mu_t, scale=s_t) ])) ax.axvline(c, color='g', label='c: critical value') ax.axvline(mu_c, color='r', alpha=0.3, linestyle='--', label='mu_c') ax.axvline(mu_t, color='b', alpha=0.3, linestyle='--', label='mu_t') ax.fill_between(support[support <= c], y2[support <= c], color='b', alpha=0.2, label='b: power') ax.fill_between(support[support >= c], y1[support >= c], color='r', alpha=0.2, label='a: significance') ax.legend(loc='upper right', prop={'size': 20}) ax.set_title('A/B test setup for sample size estimation', fontsize=20) ax.set_xlabel('Values') ax.set_ylabel('Propabilities') plt.show()

このしきい値を文字で示します 。 ランダム変数に正規分布がある場合、次の等式が当てはまります。
どこで 分位関数です。
この場合、次の2つの方程式のシステムを書くことができます。 そして したがって:
このシステムを決定した 、特定の統計的有意性と検出力を得るために各実験に誘導する必要がある十分な量のトラフィックの推定値を取得します。
たとえば、実際のコンバージョン値 、そして新しい それから 各バリエーションで2,269,319人のユーザーを誘導する必要があります。 コンバージョンが超えた場合、新しいバリエーションが受け入れられます 。 これをチェックしてください。
def get_size(theta_c, theta_t, alpha, beta): # t_alpha = stats.norm.ppf(1 - alpha, loc=0, scale=1) t_beta = stats.norm.ppf(beta, loc=0, scale=1) # n n = t_alpha*np.sqrt(theta_t*(1 - theta_t)) n -= t_beta*np.sqrt(theta_c*(1 - theta_c)) n /= theta_c - theta_t return int(np.ceil(n*n)) n_max = get_size(0.001, 0.0011, 0.01, 0.01) print n_max # , H_0 print 0.001 + stats.norm.ppf(1 - 0.01, loc=0, scale=1)*np.sqrt(0.001*(1 - 0.001)/n_max) >>>2269319 >>>0.00104881009215
したがって、有効なサンプルサイズを計算するには、マーケティング部門または別のビジネス部門に行って、次のことを確認する必要があります。
- コンバージョン値は何ですか 新しいバリエーションでは、ビジネスがコンバージョンのある古いバージョンのボタンから切り替えることを決定することがわかります 新しいものに。 新しいものが古いものよりも大きい場合、それを導入する十分な理由がすでにあると仮定するのは自然ですが、少なくともテストのためにオーバーヘッドを忘れないでください。差が小さいほど、テストに費やす必要があるトラフィックが多くなり、これが利益の損失であるためです(同時にテストが失敗するリスク);
- 許容できる有意水準は何ですか そして力 必要です(おそらく、ビジネスにこれが何を意味するのかを説明する方法がまだあります)。
受け取ったこと しきい値を簡単に計算できます 。 これは、収集する場合 各変動の観測値、および実験グループではクリック推定値 閾値以上 それから拒否します 対立仮説を受け入れます 新しいバリエーションの方が優れていることを紹介します。 この場合、次のようになります 第一種のオッズ、すなわち 誤って古いボタンを新しいボタンに置き換えることにしました。 そして 可能性としては、新しいバリエーションが優れている場合、正しいことを実行して実装しました。 しかし、最も悲しいことは、実験後にトラフィックを2つのバリエーションに分けて運転した場合、 、古いボタンを放棄する理由はないと考えています。 正確には理由はなく、新しいボタンの方が悪いことを証明しませんでした。 そのようなこと。
正直なところ、前の段落で描かれた結論はあまり説得力がなく、一般的にあなただけでなく混乱させる可能性があるように思えます。 マーケティング部門が新しいボタンの形状に関する独自の研究に数百万ルーブルを費やし、「それが良いと信じる理由はない」と言ったと想像してください。 ちなみに、理由は次のとおりです。サンプルサイズに関して方程式がどのように解かれるか、およびサンプルサイズの増加に伴って平均値の推定値の分布がどのように変化するかを説明しましょう。 アニメーションでは、サンプルサイズが増加するにつれて、平均推定値の分布範囲がどのように減少するかを観察できます。 推定値の分散が減少します。これは、この評価に自信をもって識別されます。 実際、以下の画像は少し不正です。分布が減少すると、高さも増加します。 面積は一定のままでなければなりません。
フレームをgifに接続するには、 Imagemagick変換ツールを使用します
np.random.seed(1342) p_c = 0.3 p_t = 0.4 alpha = 0.05 beta = 0.2 n_max = get_size(p_c, p_t, alpha, beta) c = p_c + stats.norm.ppf(1 - alpha, loc=0, scale=1)*np.sqrt(p_c*(1 - p_c)/n_max) print n_max, c def plot_sample_size_frames(do_dorm, width, height): left_x = c - width right_x = c + width n_list = range(5, n_max, 1) + [n_max] for f in glob.glob("./../images/sample_size_gif/*_%s.*" % ('normed' if do_dorm else 'real')): os.remove(f) for n in tqdm_notebook(n_list): s_c = np.sqrt(p_c*(1 - p_c)/n) s_t = np.sqrt(p_t*(1 - p_t)/n) c_c = p_c + stats.norm.ppf(1 - alpha, loc=0, scale=1)*s_c c_t = p_t + stats.norm.ppf(beta, loc=0, scale=1)*s_t support = np.linspace(left_x, right_x, 1000) y_c = stats.norm.pdf(support, loc=p_c, scale=s_c) y_t = stats.norm.pdf(support, loc=p_t, scale=s_t) if do_dorm: y_c /= max(y_c.max(), y_t.max()) y_t /= max(y_c.max(), y_t.max()) fig, ax = plt.subplots() ax.plot(support, y_c, color='r', label='y control') ax.plot(support, y_t, color='b', label='y treatment') ax.set_ylim(0, height) ax.set_xlim(left_x, right_x) ax.axvline(c, color='g', label='c') ax.axvline(c_c, color='m', label='c_c') ax.axvline(c_t, color='c', label='c_p') ax.axvline(p_c, color='r', alpha=0.3, linestyle='--', label='p_c') ax.axvline(p_t, color='b', alpha=0.3, linestyle='--', label='p_t') ax.fill_between(support[support <= c_t], y_t[support <= c_t], color='b', alpha=0.2, label='b: power') ax.fill_between(support[support >= c_c], y_c[support >= c_c], color='r', alpha=0.2, label='a: significance') ax.legend(loc='upper right', prop={'size': 20}) ax.set_title('Sample size: %i' % n, fontsize=20) fig.savefig('./../images/sample_size_gif/%i_%s.png' % (n, 'normed' if do_dorm else 'real'), dpi=80) plt.close(fig) plot_sample_size_frames(do_dorm=True, width=0.5, height=1.1) plot_sample_size_frames(do_dorm = False, width=1, height=2.5) !convert -delay 5 $(for i in $(seq 5 1 142); do echo ./../images/sample_size_gif/${i}_normed.png; done) -loop 0 ./../images/sample_size_gif/sample_size_normed.gif for f in glob.glob("./../images/sample_size_gif/*_normed.png"): os.remove(f) !convert -delay 5 $(for i in $(seq 5 1 142); do echo ./../images/sample_size_gif/${i}_real.png; done) -loop 0 ./../images/sample_size_gif/sample_size_real.gif for f in glob.glob("./../images/sample_size_gif/*_real.png"): os.remove(f)
不正行為のアニメーション:
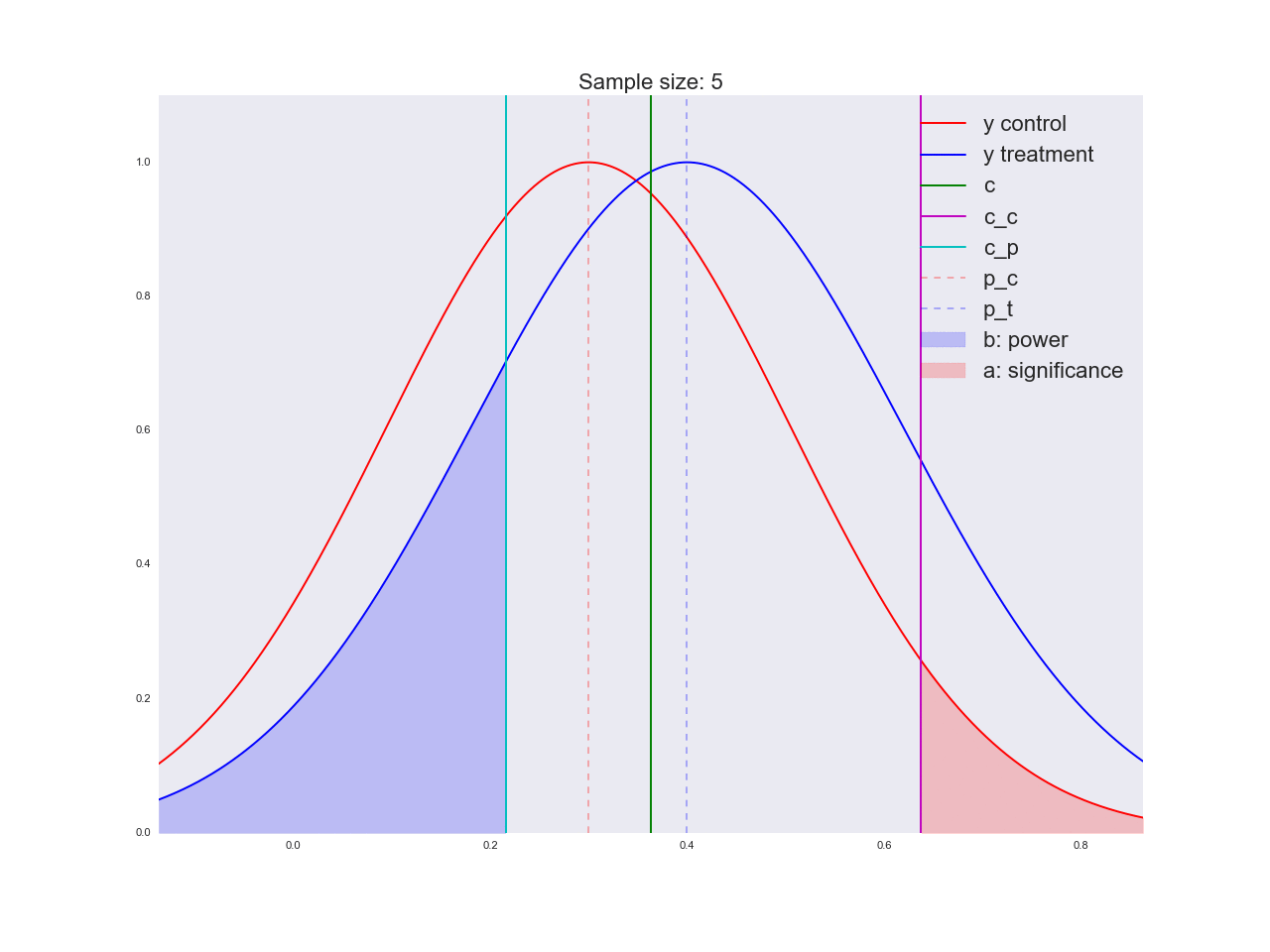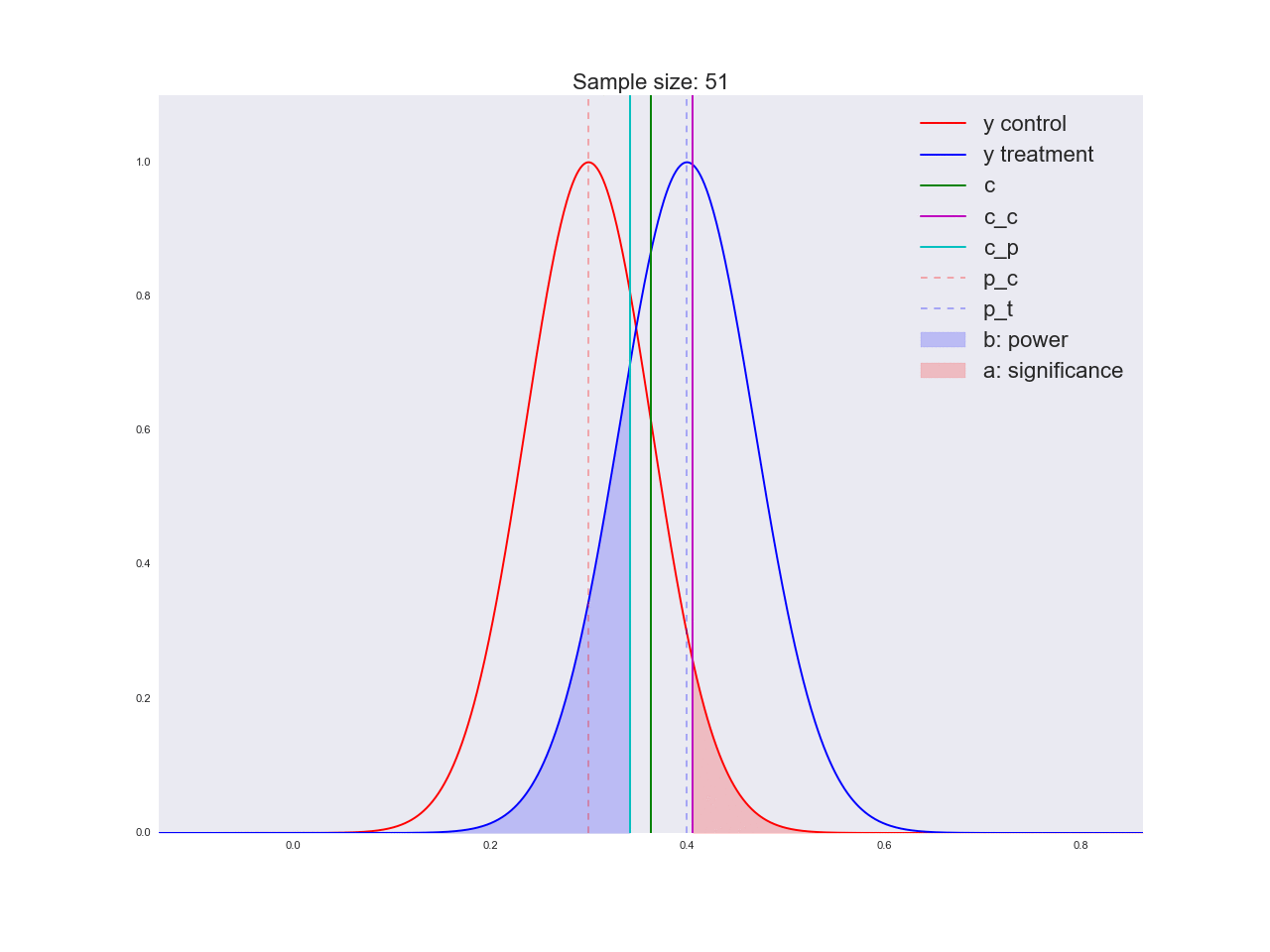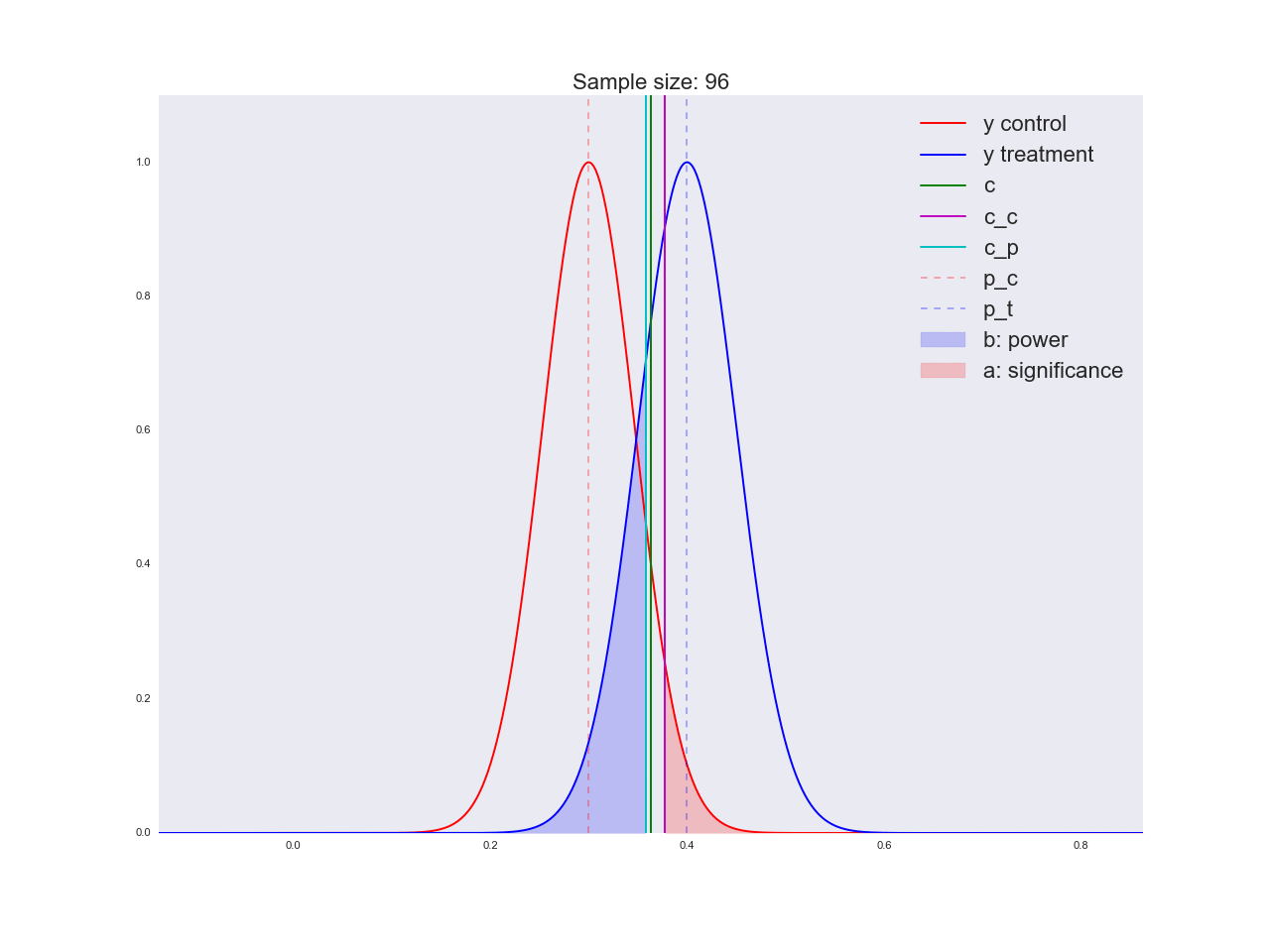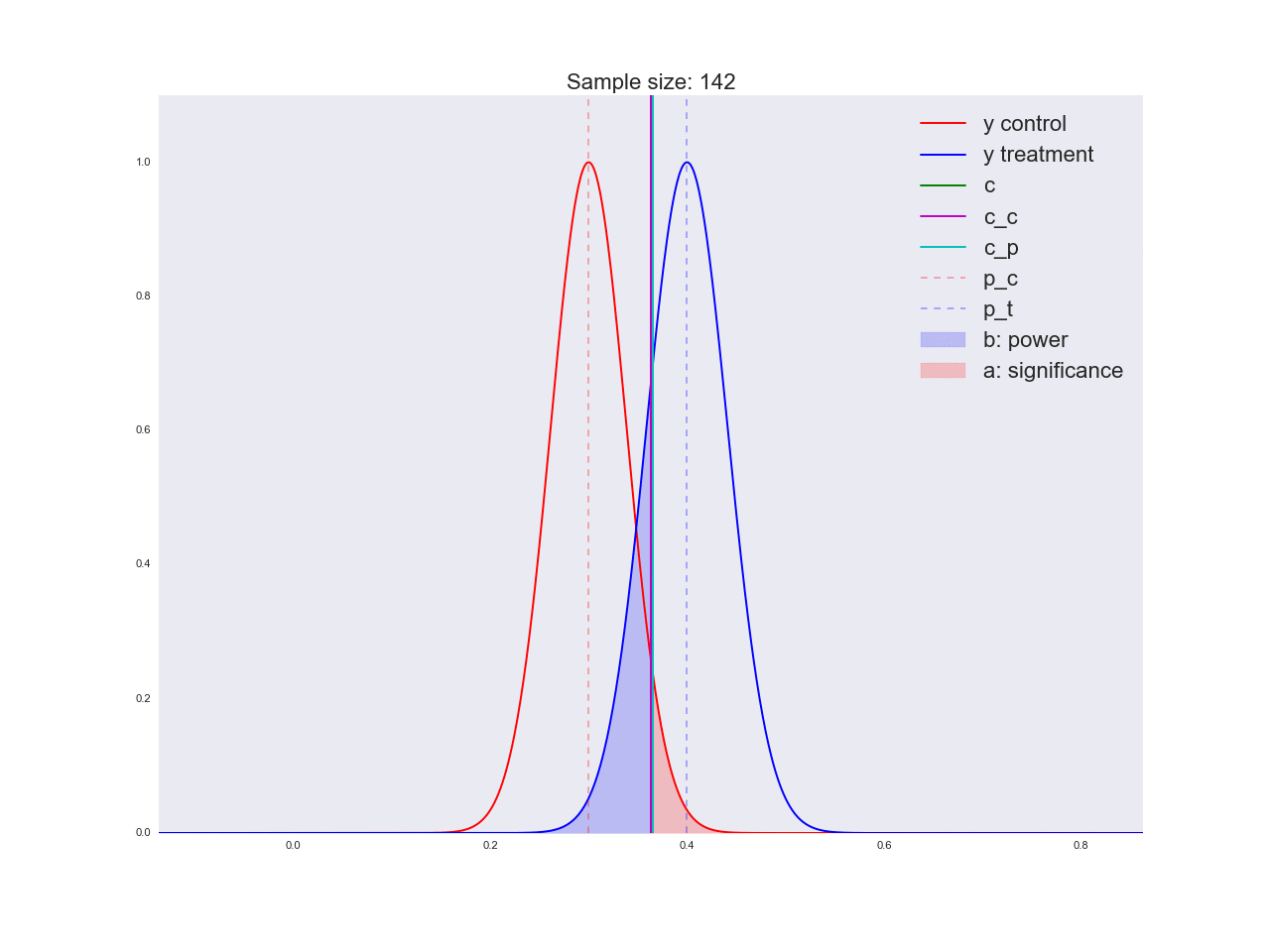
実際のアニメーション:
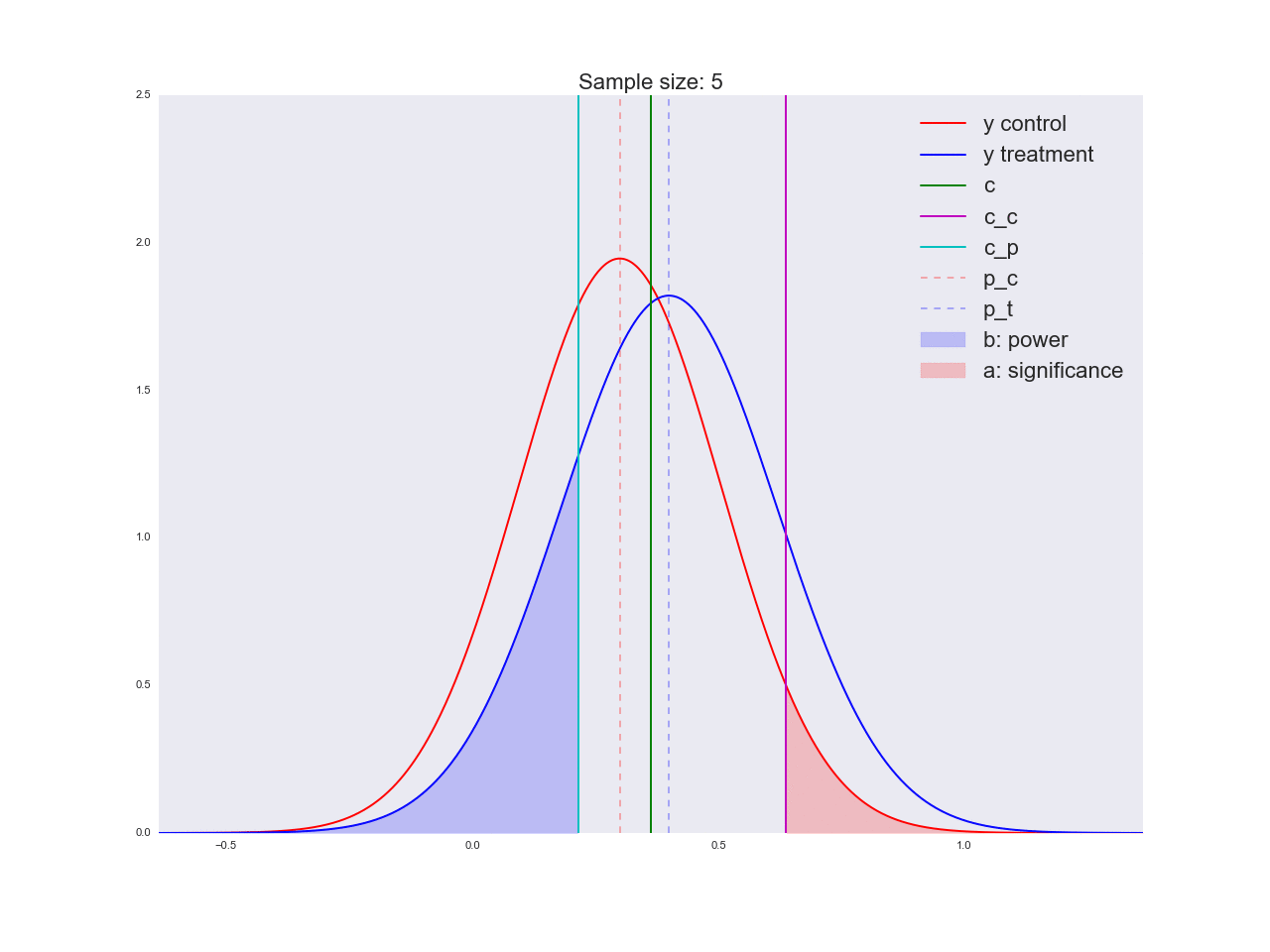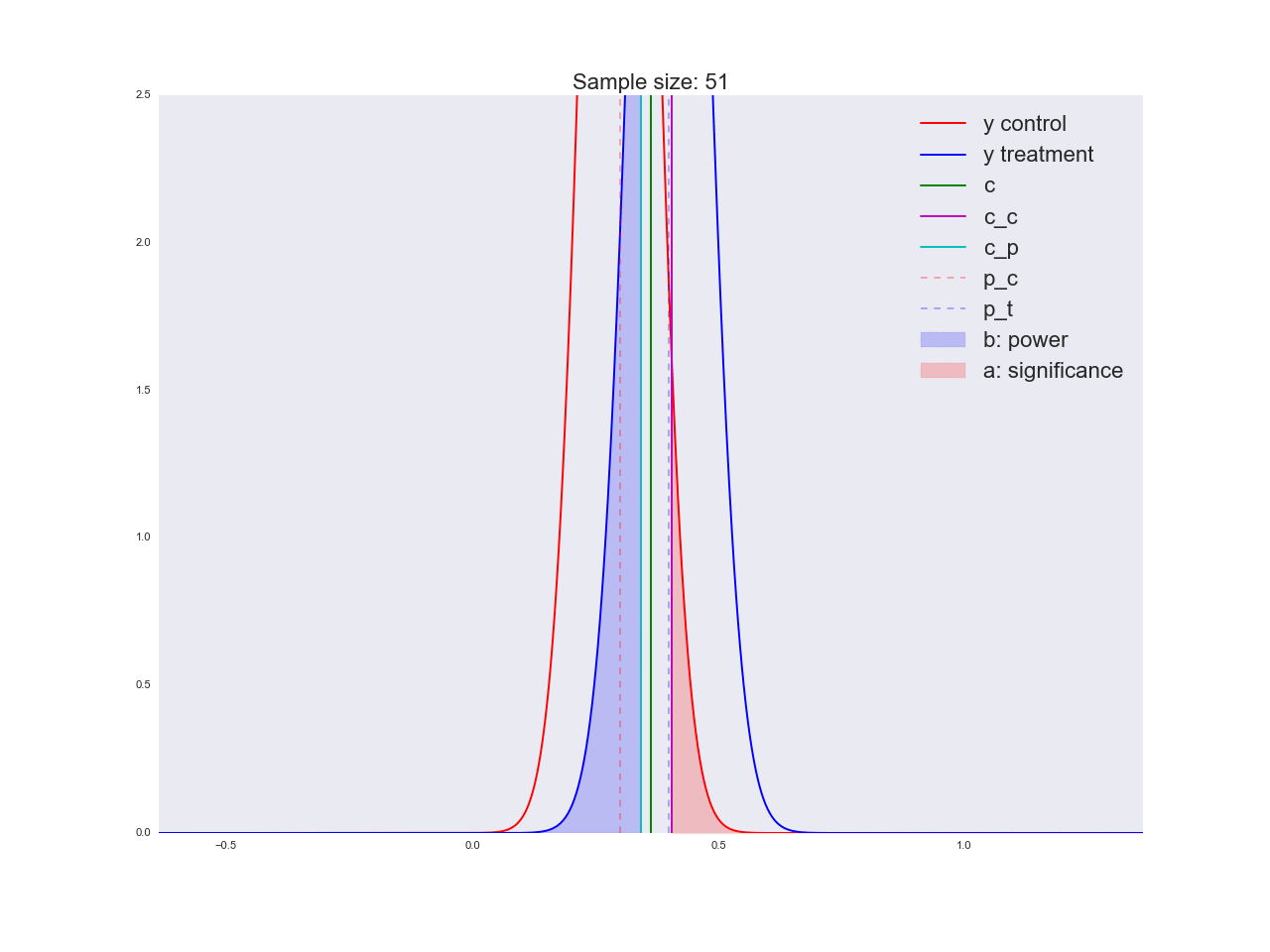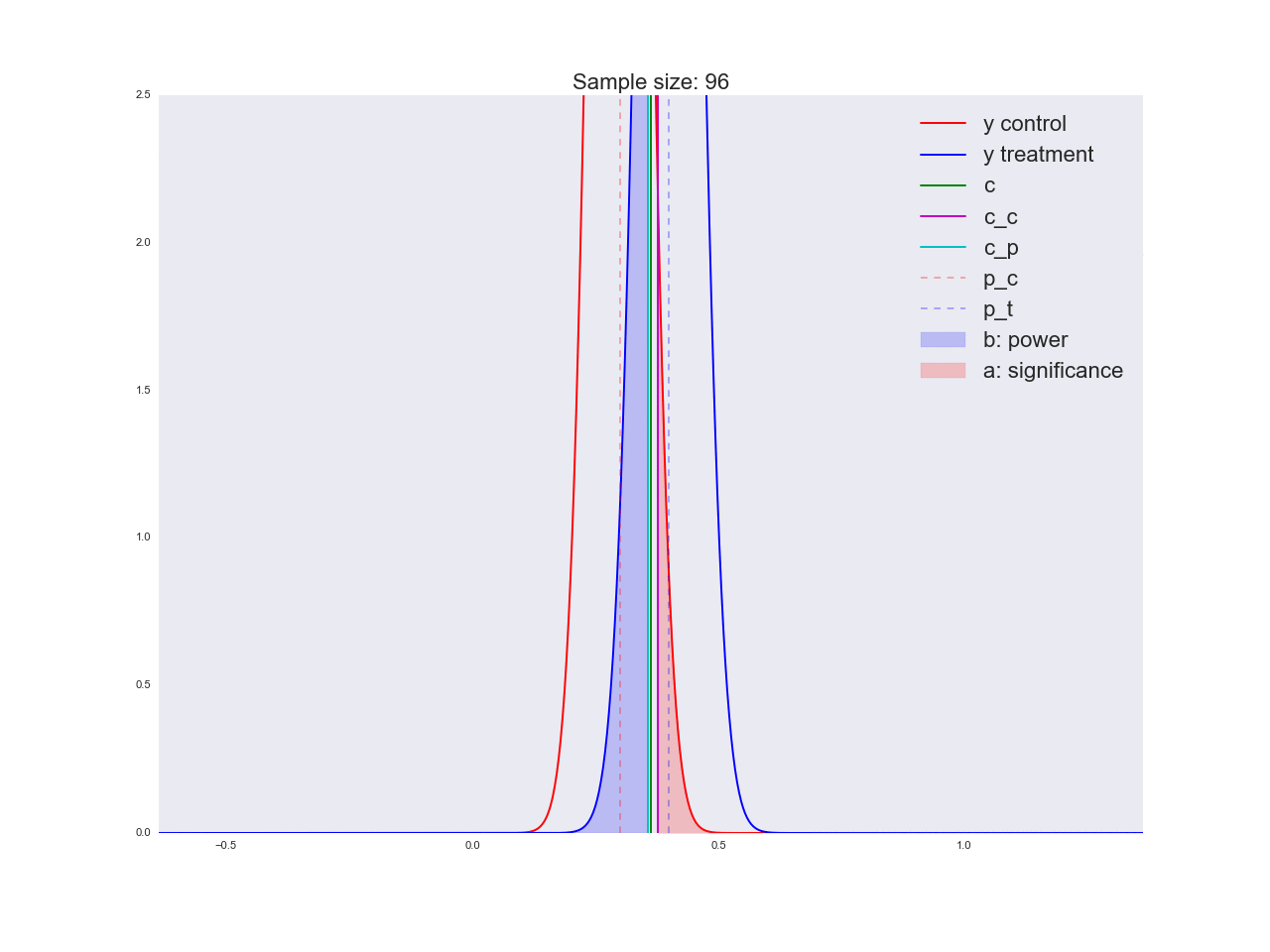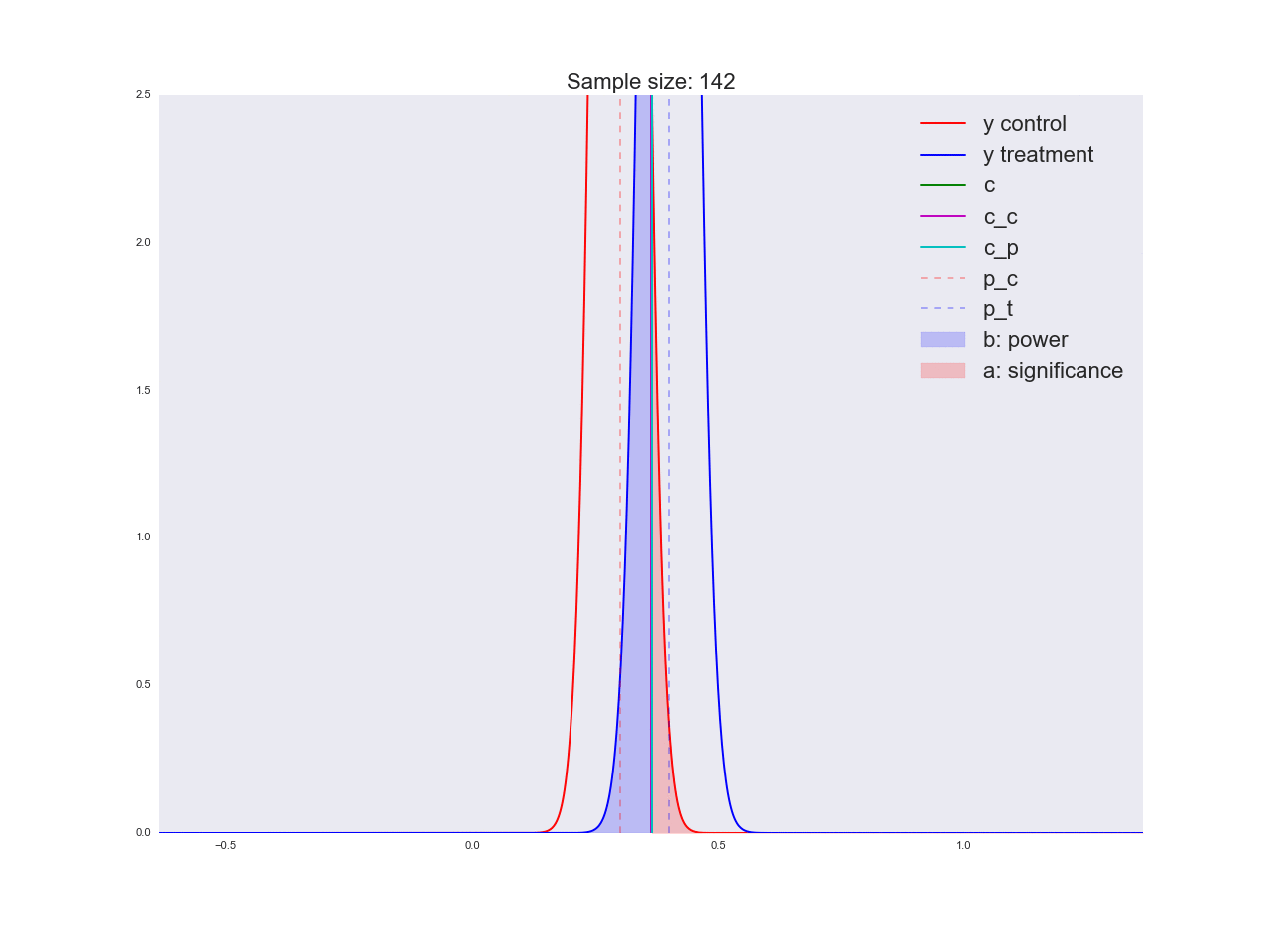
A / B / nテストに関するセクションの最後で、nについて話しましょう。 冒頭で、現在の変動に加えて、4つの対立仮説があると述べました。 上記の実験のデザインは、n個のバリエーションに簡単にスケーリングできます。この場合、5個しかありません。トラフィックを5つの部分に分割し、少なくとも1つがクリティカルしきい値を超える偏差を調べることを除いて、何も変わりません 。 しかし、私たちは皆、最良の選択肢はただ一つの選択肢であることを確実に知っています。 (どこ -バリエーションの数)を明らかに悪いバリエーションに変更しますが、どれが悪いかはまだわかりません。 そして、悪いバリエーションを狙った各ユーザーは、良いバリエーションを狙ったユーザーよりも利益が少なくなります。 次のセクションでは、オンラインテストで非常に効果的な代替実験計画法を検討します。
さて、A / B / n検定の実施の難しさを最終的に解決するために、多重仮説検定の結果の有意性の可能な修正の1つを検討します。 たとえば、 、そして実験には5つのテストがあります。
すべてのテストが重要ではない場合でも、とにかく 意味のある結果を誤って取得する可能性。 意外とそうですか? それを理解してみましょう。 私たちが持っているとしましょう 1つの実験でテストします。 それぞれに独自のp値があります。 (誤って拒否する確率 、これは私たちの ) で有意水準を下げるとどうなりますか 回:
次に、少なくとも1つの結果が重要である確率が初期値になります 。 チェック:
このトリックは、Bonferonni Hill Amendmentと呼ばれます。 したがって、仮説が多いほど、必要な有意水準が低くなり、各テストでより多くのユーザーをキャッチする必要があります。 前の例に戻ると、 2,269,319人のユーザーが必要でしたが、修正により、各バリエーションに2,525,873人のユーザーが必要でした 。 そして、これ、一分間、ほとんど 実験全体のトラフィックが増加します。 すべての可能な修正を掘り下げると、統計に関する小さな本を入手できます。 そのようなこと。

2012年には、洗練されたツールと簡単な統計情報を使用して、死んだサケであっても関連する脳活動を検出できるという事実により、 多くの著者が神経生物学でシュノベル賞を受賞しました。 どうして? すべては、著者がMRI装置をテストしなければならなかったという事実から始まりました。 通常、油で満たされたボールが取られ、スキャンされます。 しかし、著者はそれがなんとなく平凡で楽しいものではないと判断しました。 そのうちの1人は、市場でアトランティックサーモンの死体全体を購入しました。 彼らは魚をMRI装置に入れ、日常生活の人々の画像を見せ始めました。
仕事は、一般に、死んだサケの脳に人と一緒に画像を見せることで活動が起こらないことを示すことでした。 MRIデバイスは、ボクセルのある原子単位である膨大なデータの配列を返します。基本的には、スキャンされたオブジェクトが分割される小さなデータの立方体です。 脳全体の活動を研究するために、各ボクセルに関する仮説の複数のテストを実施する必要があります(テストと同様ですが、より多くのテストのみ)。 そして、もしあなたがボンフェロニ補正を行わなければ、サケでは刺激と脳反応の間には相関があることが判明しました。 死んだサケは刺激に反応します。 しかし、修正を行うと、死んだサーモンは死んだままになります。
多くの人がシュノベル賞は楽しいと思っていますが、科学に本当に貢献したのはこの作品でした。 著者は神経生物学に関する記事を2010年まで分析しましたが、著者の約40%が多重仮説検定で補正を使用していないことが判明しました。 サーモンに関する記事の公開後、修正を使用しない神経科学の記事の数は10%に減少しました。
ベイジアン多腕バンディット
盗賊はA / Bテストの普遍的な代替品ではありませんが、特定の領域では優れた代替品であることに注意してください。 A / Bテストは1世紀以上前に登場し、医学、農業、経済学などのさまざまな分野で仮説をテストするために常に使用されてきました。これらすべての分野には、いくつかの共通要因があります。
- 1つの実験のコストは大きいです(恐ろしい病気の新しい治療法を想像してください:それを生産することに加えて、薬かプラセボかを知らずにピルを服用することに同意する人々を見つける必要もあります);
- 間違いは非常に高価です(繰り返しますが、医学からの事実:10年の研究の後に、製薬会社が市場で機能しない製品を発売した場合、この農場会社とそれを信頼する人々はおそらく終了します)。
A / Bテストは、古典的な実験に最適です。 これにより、テストのサンプルサイズを見積もることができ、事前に予算を見積もることもできます。 また、必要なエラーレベルを設定することもできます。たとえば、医師は非常に小さな そして 一方、他の人は権力についてそれほど心配していないが、重要性について心配している。 たとえば、新しいハンバーガーレシピをテストする場合、古いものよりも本当に悪い場合は新しいものを提出したくありません。 しかし、他の方法でミスをした場合、つまり 新しいレシピは優れていますが、受け入れませんでした。簡単に生き残ることができます。 今日まで、私たちは何とかこれと一緒に暮らし、壊れませんでした。 問題は、実験に費やす準備ができている予算だけにかかっています。それが私たちに無限であれば、もちろん、両方のしきい値をゼロにして数百万の実験を追い出すのが簡単です。
しかし、オンライン実験の世界では、すべてが古典的な実験ほど重要ではありません。 エラー価格はゼロに近く、実験価格もゼロに近いです。 はい、これはA / Bテストを使用する可能性を排除しません。 しかし、仮説をテストして答えを出すだけでなく、おそらくどちらが優れているかだけでなく、どのバリエーションが優れているかの見積もりを動的に変更し、最終的にこのまたはそのバリエーションに送信するトラフィックの量を決定するより良いオプションがあります与えられた時間に。

一般に、これは機械学習で共存しなければならない多くの妥協の1つです。この場合は、他のオプションと最良の悪用の比較です(探索と悪用のトレードオフ)。 2つ以上の仮説(ボタンのバリエーション)をテストするプロセスでは、意図的に誤ったオプションに大量のトラフィックを送信したくありません(A / Bテストの場合、各バリエーションに等しいシェアを送信します)。 しかし、同時に、他のバリエーションをフォローしたいと思います。最初に運が悪かった場合、またはモードがボタンの色に変わった場合、これを感じて状況を修正できました。 ベイジアンの盗賊が私たちを助けます。 ここにあります。

説明されているデザインは、カジノに来たときの状況に非常に似ており、目の前には「ワンアームバンディット」などのスロットマシンがたくさんあります。 お金と時間に限りがあり、できるだけ費用をかけずに、すぐに最適なマシンを見つけたいと考えています。 この問題の声明は、多腕バンディット問題と呼ばれます。 このタスクには多くのアプローチがあり、単純なものから 可能性がある場合の貪欲な戦略 現在の瞬間にあなたに最大の利益をもたらしたペンを引き出し、確率で ランダムな手を引く(スロットマシンのレバーを意味する)。 最適でないハンドでプレーするときの損失の分析に基づいた、より複雑な方法があります。 しかし、 トンプソンサンプリングとベイズの定理に基づく別の方法を検討します。 この方法はそれほど新しいものではありませんが(1933)、オンライン実験の時代にのみ普及しました。 Yahooは、この方法を使用して2010年代初頭にニュースフィードをパーソナライズした最初の企業の1つでした。 その後、Microsoftは盗賊を使ってBing検索結果のCTRバナーを最適化し始めました。 原則として、現代のオンライン調査に関する記事の大部分は彼らによって書かれています。 ところで、問題のステートメントは強化トレーニングに非常に似ていますが、1つの例外があります:盗賊の問題のステートメントでは、エージェントは環境を変更できず、一般的な強化トレーニングでは、エージェントが環境に影響を与える可能性があります。
ギャングスターのタスクを正式化します。 時間までに 一連の報酬を観察します 。 実行されたアクションを示します どうやって (バンディットインデックス、ボタンの色)。 また、それぞれ ギャングの報酬の何らかの分布から独立して生成された どこで パラメータのベクトルです。 クリック分析の場合、報酬はバイナリであるという事実によってタスクが単純化されます 、およびパラメーターベクトルは、各バリエーションのベルヌーイ分布パラメーターです。
その後、盗賊の予想報酬 なります 。 分布パラメーターがわかっていれば、予想される報酬を簡単に計算し、常に最大の報酬を持つオプションを選択するだけです。 しかし、残念ながら、分布の真のパラメーターは不明です。 また、クリックの場合 、および予想される報酬 。 この場合、ベルヌーイ分布パラメーターにアプリオリ分布を導入し、各アクションの後、報酬を観察して、バンディットの「信仰」を更新できます ベイズの定理を使用します。 ベータ配布は 、次の3つの理由から理想的です。
- ベータ分布は、ベルヌーイ分布のアプリオリ共役です 。 事後分布もベータ分布の形をしていますが、パラメーターは異なります。
- で ベータ分布は均一分布の形を取ります。 完全に不確実な状況で使用するのが自然なもの(たとえば、テストの最初); 盗賊の収益性に関する我々の期待がより確実になるほど、分布はより面白くなる(左は収益性のある盗賊ではなく、右は収益性がある)。
- モデルの解釈は簡単です 成功したトライアルの数、および -失敗した試行の数。 平均値は 。
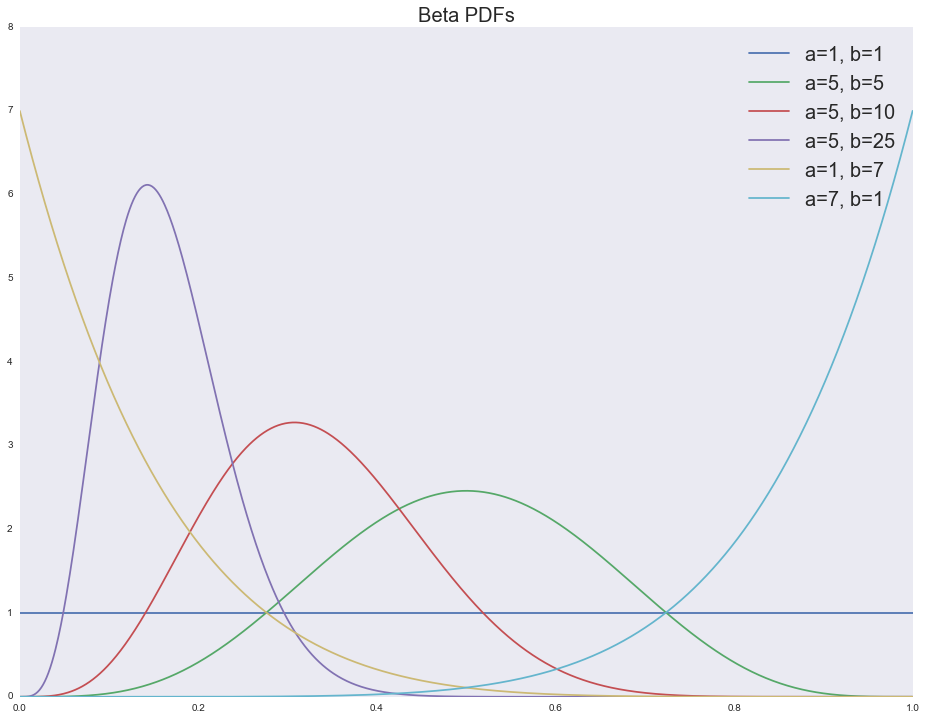
さまざまなベータ分布パラメーターの密度関数を見てみましょう。
support = np.linspace(0, 1, 1000) fig, ax = plt.subplots() for a, b in [(1, 1), (5, 5), (5, 10), (5, 25), (1, 7), (7, 1)]: ax.plot(support, stats.beta.pdf(support, a, b), label='a=%i, b=%i' % (a, b)) ax.legend(loc='upper right', prop={'size': 20}) ax.set_title('Beta PDFs', fontsize=20)
, , . -. , :
, : ( ) ( ) , . , , , :
- - ;
-
- ;
- ;
- - ( , );
- ( batch mode, , ):
-
-
, . Beta-Bernoulli , .. で , , . , :
- , , ; , , , ;
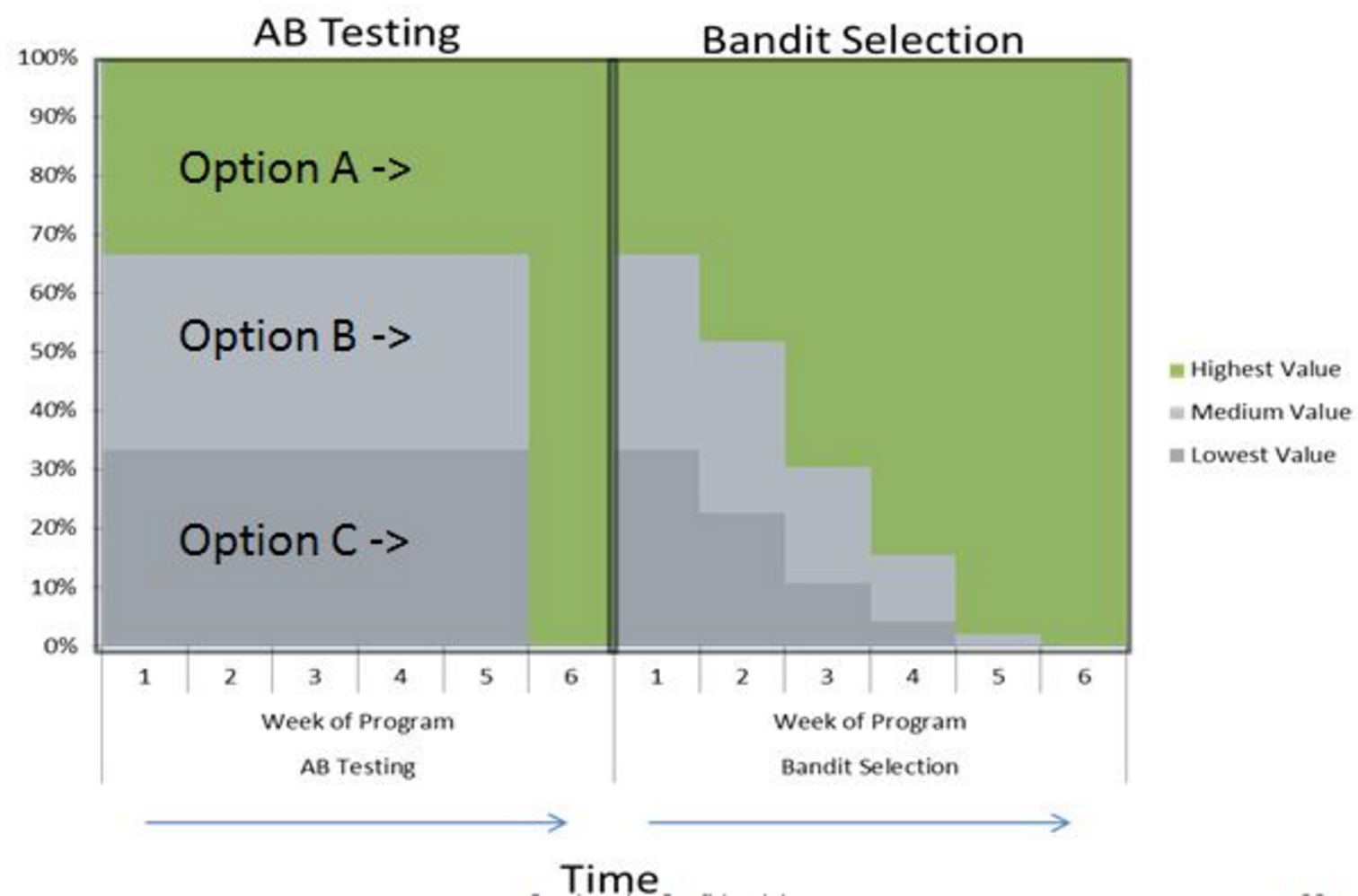
- ( -), , ;
- , , , , , CTR, .
実験
. , , . , A/B/n-, .
# n_variations = 5 # n_switches = 5 # n_period_len n_period_len = 2000 # # , , , n_period_len p_true_periods = np.array([ [1, 2, 3, 4, 5], [2, 3, 4, 5, 1], [3, 4, 5, 2, 1], [4, 5, 3, 2, 1], [5, 4, 3, 2, 1]], dtype=np.float32).T**3 p_true_periods /= p_true_periods.sum(axis=0) # ax = sns.heatmap(p_true_periods) ax.set(xlabel='Periods', ylabel='Variations', title='Probabilities of variations') plt.show()

: , . , n_period_len
.
( ). , — ( ). , ( / — ); , . ( ), , , , . : , ( ) . . , ( , .. — ). .
x_support = np.linspace(0, 1, 1000) alpha = dict([(i, [1]) for i in range(n_variations)]) beta = dict([(i, [1]) for i in range(n_variations)]) cmap = plt.get_cmap('jet') colors = [cmap(i) for i in np.linspace(0, 1, n_variations)] actionspp = [] for ix_period in range(p_true_periods.shape[1]): p_true = p_true_periods[:, ix_period] is_converged = False actions = [] for ix_step in range(n_period_len): theta = dict([(i, np.random.beta(alpha[i][-1], beta[i][-1])) for i in range(n_variations)]) k, theta_k = sorted(theta.items(), key=lambda t: t[1], reverse=True)[0] actions.append(k) x_k = np.random.binomial(1, p_true[k], size=1)[0] alpha[k].append(alpha[k][-1] + x_k) beta[k].append(beta[k][-1] + 1 - x_k) expected_reward = dict([(i, alpha[i][-1]/float(alpha[i][-1] + beta[i][-1])) for i in range(n_variations)]) estimated_winner = sorted(expected_reward.items(), key=lambda t: t[1], reverse=True)[0][0] print 'Winner is %i' % i actions_loc = pd.Series(actions).value_counts() print actions_loc actionspp.append(actions_loc.to_dict()) for i in range(n_variations): plt.axvline(x=p_true[i], color=colors[i], linestyle='--', alpha=0.3, label='true value of %i' % i) plt.plot(x_support, stats.beta.pdf(x_support, alpha[i][-1], beta[i][-1]), label='distribution of %i' % i, color=colors[i]) plt.legend(prop={'size': 20}) plt.title('Period %i; winner: true is %i, estimated is %i' % (ix_period, p_true.argmax(), estimated_winner), fontsize=20) plt.show() actionspp = dict(enumerate(actionspp))
:
Winner is 4 4 1953 3 19 2 12 1 8 0 8 dtype: int64
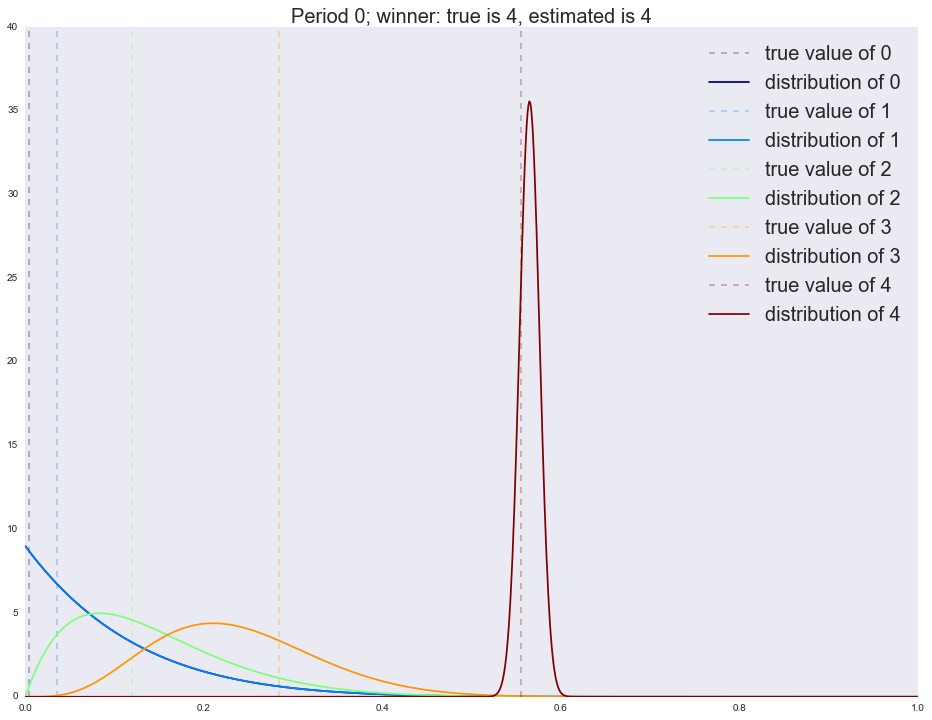
:
Winner is 4 3 1397 4 593 1 6 2 3 0 1 dtype: int64
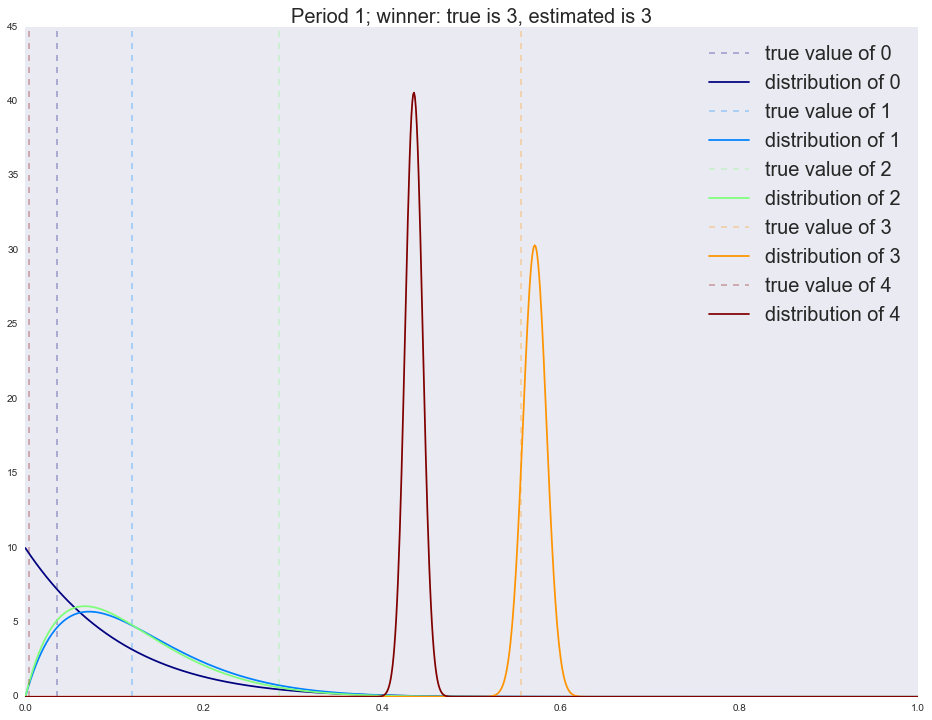
:
Winner is 4 2 1064 3 675 4 255 1 3 0 3 dtype: int64
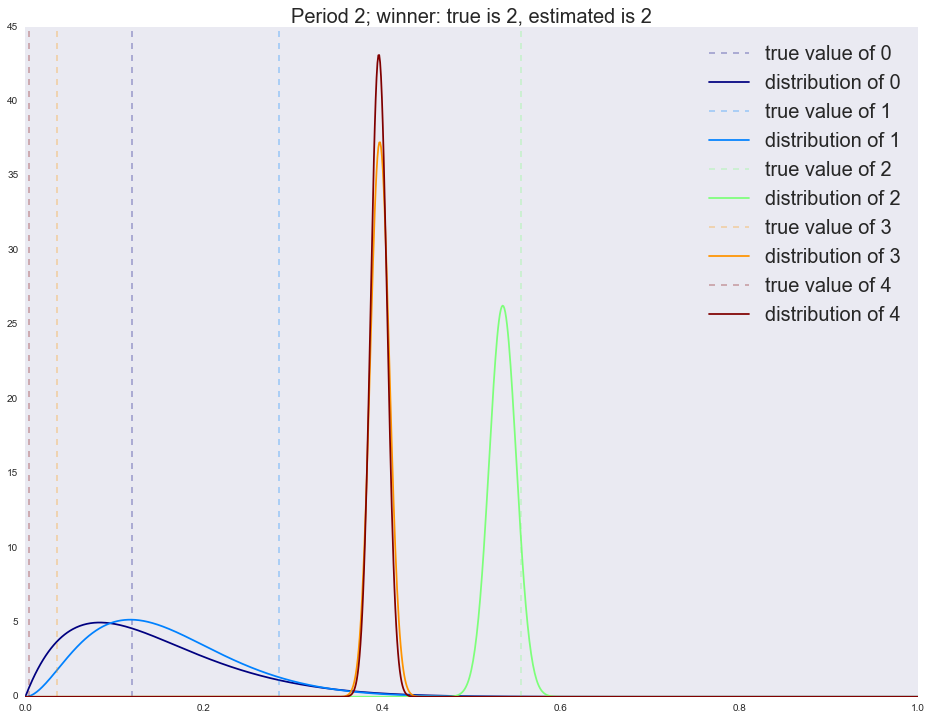
:
Winner is 4 1 983 2 695 4 144 3 134 0 44 dtype: int64
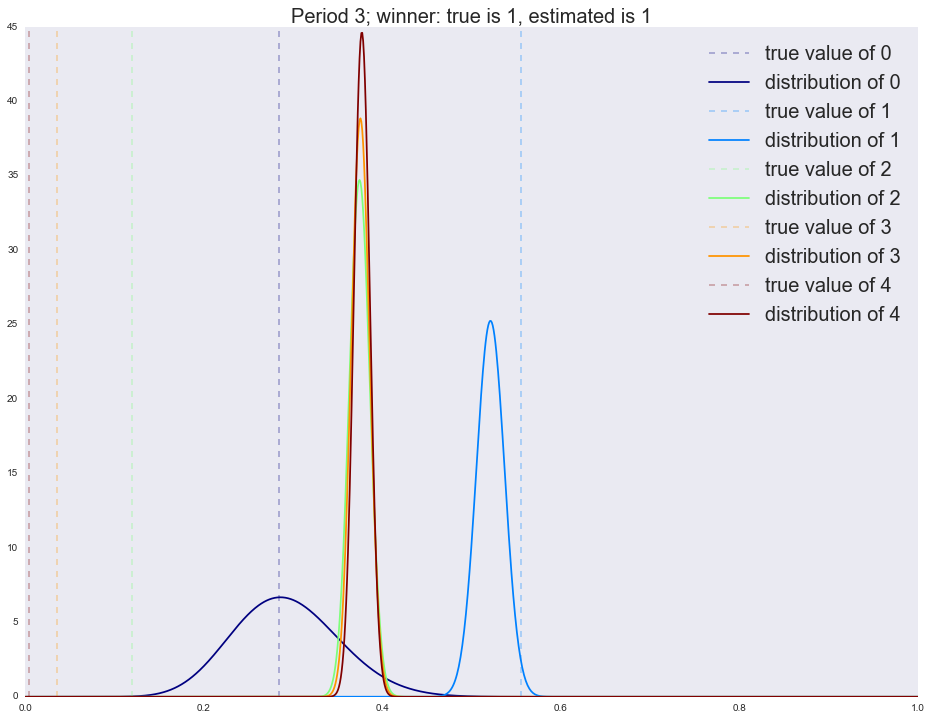
:
Winner is 4 1 1109 0 888 4 2 2 1 dtype: int64

, .
df = [] for pid in actionspp.keys(): for vid in actionspp[pid].keys(): df.append({ 'Period': pid, 'Variation': vid, 'Probapility': actionspp[pid][vid]/1000.0 }) df = pd.DataFrame(df) ax = sns.barplot(x="Period", y="Probapility", hue="Variation", data=df) ax.set(title="Ratio of traffic used for variations per period") plt.show()
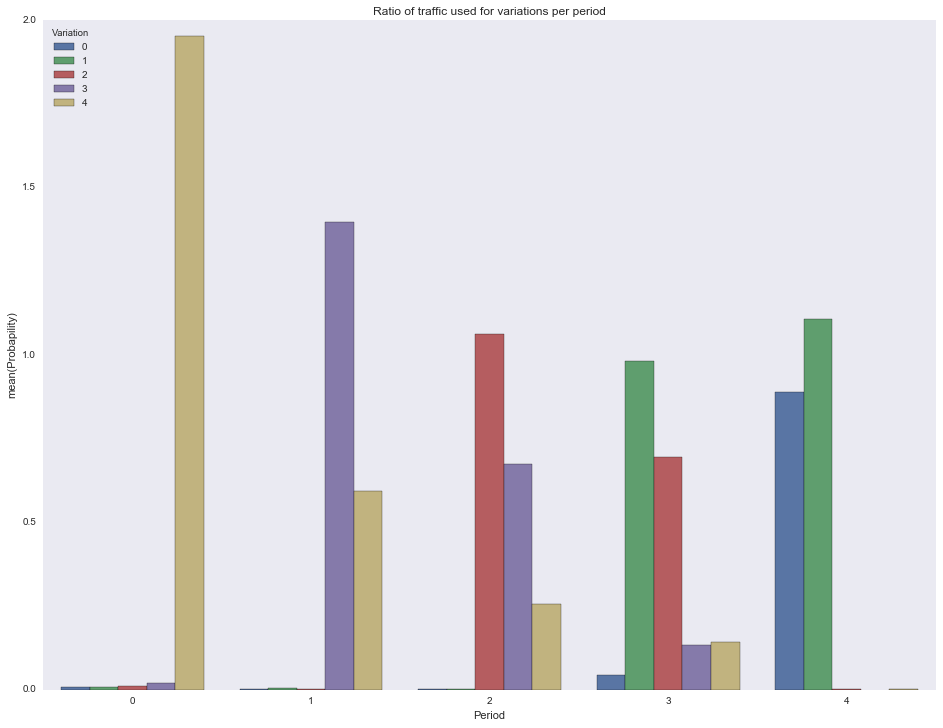
.
n_period_len = 3000 alpha = dict([(i, [1]) for i in range(n_variations)]) beta = dict([(i, [1]) for i in range(n_variations)]) decay = 0.99 plot_step = 25 for f in glob.glob("./../images/mab_gif/*.png"): os.remove(f) img_ix = 0 height = 10 # 15 for ix_period in range(p_true_periods.shape[1]): p_true = p_true_periods[:, ix_period] is_converged = False actions = [] for ix_step in tqdm_notebook(range(n_period_len)): if ix_step % plot_step == 0: expected_reward = dict([(i, alpha[i][-1]/float(alpha[i][-1] + beta[i][-1])) for i in range(n_variations)]) estimated_winner = sorted(expected_reward.items(), key=lambda t: t[1], reverse=True)[0][0] fig, ax = plt.subplots() ax.set_ylim(0, height) ax.set_xlim(0, 1) for i in range(n_variations): ax.axvline(x=p_true[i], color=colors[i], linestyle='--', alpha=0.3, label='true value of %i' % i) ax.plot(x_support, stats.beta.pdf(x_support, alpha[i][-1], beta[i][-1]), label='distribution of %i' % i, color=colors[i]) ax.legend(prop={'size': 20}) ax.set_title('Period %i, step %i; winner: true is %i, estimated is %i' % (ix_period, ix_step, p_true.argmax(), estimated_winner), fontsize=20) fig.savefig('./../images/mab_gif/%i.png' % img_ix, dpi=80) img_ix += 1 plt.close(fig) theta = dict([(i, np.random.beta(alpha[i][-1], beta[i][-1])) for i in range(n_variations)]) k, theta_k = sorted(theta.items(), key=lambda t: t[1], reverse=True)[0] actions.append(k) x_k = np.random.binomial(1, p_true[k], size=1)[0] alpha[k].append(alpha[k][-1] + x_k) beta[k].append(beta[k][-1] + 1 - x_k) if decay > 0: for i in range(n_variations): if i == k: continue alpha[i].append(max(1, alpha[i][-1]*decay)) beta[i].append(max(1, beta[i][-1]*decay)) print img_ix for f in glob.glob("./../images/mab_gif/mab.gif"): os.remove(f) !convert -delay 5 $(for i in $(seq 1 1 600); do echo ./../images/mab_gif/$i.png; done) -loop 0 ./../images/mab_gif/mab.gif for f in glob.glob("./../images/mab_gif/*.png"): os.remove(f)
おわりに
, -:
- ;
- , , , ;
- , , , .

: , ? .
bauchgefuehl , arseny_info yorko .