
あるサイト、あるフォーラムでは、SciFiというあだ名の良い仲間が彼の話でチームを困惑させました。
彼は、Texas Instruments [FSK変調およびMSP430マイクロコントローラーによる復調]の外国企業の技術マニュアルで、必要なデジタルフィルターを見つけました。 しかし、外国人は非常にunningであることが判明し、ソースコードで次のように言及しました:
************************************************** * Running this filter takes 113 cycles ************************************************** ;***************************************************** ; New simpler filter at following specification ; Freq_Stop: 2.5KHz, Attenuation_Stop: 40dB ; Freq_Pass: 1.4KHz, Attenuation_Pass: 1dB ; Order of filter = 5 ;***************************************************** filters: bis #INTERRUPT_TOGGLE,global_status mov #WDF_PARMS,mem_ptr .word 4f16h .word 0000h .word 498fh .word 0000h .word 4f17h .word 0008h .word 8607h .word 4708h .word 1108h .word 4806h .word 1108h .word 1108h .word 1108h .word 1108h .word 1108h . . .
悪魔は暗号化されました! しかし、優れた仲間のSciFiも見逃しませんでした。 彼は彼らのトリックを打ち負かし、暗号をC言語に翻訳しました。
signed short filter(signed short x) { static signed short fltmem[5]; signed short r6, r7, r9; r7 = fltmem[4] - fltmem[0]; fltmem[0] = x; r6 = (r7 >> 1) - (r7 >> 6) - fltmem[4]; fltmem[4] = fltmem[3]; fltmem[3] = r6; r6 -= r7; r7 = fltmem[2] - x; r9 = (r7 >> 3) - (r7 >> 6) + fltmem[2]; r7 -= r9; fltmem[2] = fltmem[1]; fltmem[1] = r7; return (r6 - r9)>>1; }
判明したように、悪魔は2回暗号化されました。 このコードはコンパイラを使用して明示的に取得されるため、相対アドレス指定を使用できるのはコンパイラのみです。 しかし、コード自体は関心と尊敬に値します。 ご覧のとおり、乗算演算は含まれておらず、最も単純なプロセッサーでも効果的に実行できます。 優れた仲間のSciFiと他のすべての人は、「これはどのようなフィルターですか?」という質問がありました。
このようなコードでフィルターの構造図を復元することは、可能であれば非常に面倒です。 したがって、私たちは反対に行きます。 振幅周波数特性(AFC)によってフィルターのタイプとパラメーターについて結論を導きます。 入手方法 はい、2バイトを送信する方法。
このフィルターは、無限のインパルス応答を持つフィルターであることにすぐに注意してください。 これはソースコードで推測され、フィルターの状態は配列static signed short fltmem [5]に格納されます。
フィルターのインパルス応答、つまり単一インパルスに対するフィルターの応答のサンプルを60個取得します。 しかし、整数演算の条件では、最終結果を最高の精度で取得するために、フィルターの値を1ではなく10,000のフィルターの入力に渡します。より正確には、オーバーフローを引き起こさない最大数を指定する必要があります。
インパルス応答のテストコード:
printf("%d\r\n", filter(10000)); for(int i=1;i<100;i++) { printf("%d\r\n", filter(0)); }
コピー&ペーストを使用した結果は、数学パッケージMathCadで処理されます。
インパルス応答をプロットします。 0〜20サンプルの間隔では、次のようになります。

また、20〜60サンプルの間隔では、次のようになります。
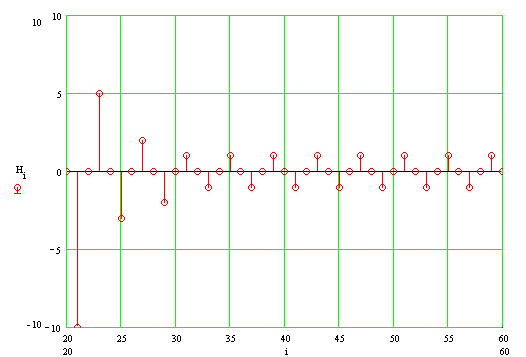
インパルス応答の分析は、フィルターに欠点がないわけではないことを示しています。 インパルス応答には、振幅が1つの離散的な非減衰振動が含まれます。 無限の特性を持つフィルターの合成理論[Goldenberg L. M. et al。Digital signal processing。 M。:Radio and communication、1985]このような発振は、通常、整数の丸め誤差によって生じるリミットサイクルと呼ばれます。
検討中のフィルターの複素伝達係数は、インパルス応答のフーリエ変換として定義できます。 離散インパルス応答の場合にのみ、時間軸上の積分をすべての非ゼロサンプルの加算に置き換えることができます。 この場合、ケースの複素透過係数は次の式で決定されます。
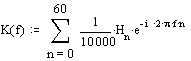
ここで、Hはインパルス応答のサンプルの配列です。
fは、サンプリングレートに正規化された周波数です。
複素伝達係数のモジュール、振幅周波数特性を対数スケール(LAC)でプロットします。 以下、プロットするときは、サンプリング周波数に対して正規化された周波数が使用されます。
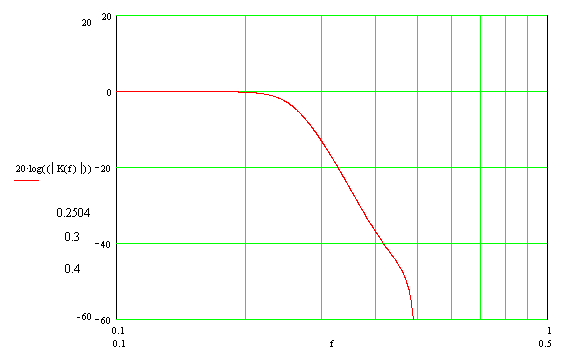
数学パッケージの組み込みツールを使用して、周波数応答のキーポイントを決定します。
- -3dB-0.25のレベルでのフィルターカットオフ周波数
- 0.3--13.266dBの周波数での透過係数
- 0.4--37.013dBの周波数での透過係数
したがって、通過帯域外の特性の勾配は次のとおりです。
 Db /ディケード
Db /ディケード
完全を期すために、位相周波数特性(PFC)を示します。

周波数0.48での位相シフトは(180 + 180 + 87)= 447度です。 アークタンジェントの曖昧さを忘れると、グラフ上の位相の不連続性が混乱を招く可能性があります。
また、図を完成させるために、グループ遅延時間(GWP)を指定します。

これで、深く考えて、 「このフィルターとは」という質問に答えることができます。
フィルター次数。 対数振幅周波数特性の分析から、このフィルターは10次リンクであり、通過帯域外の特性の勾配は約20 * 10 = 200 dB /ディケードであると仮定できます。 しかし、位相特性の分析は、位相シフトが90 * 5 = 450度になる傾向があることを示しています。 ここでは、経験の浅い「フィルターの推測」が、このリンクの必然的な位相の性質についての考えを思いがけず引き起こします。 しかし、「アナログ」周波数がタンジェントを介して「デジタル」にマッピングされることを忘れないでください。したがって、アナログ世界の法則(20dB /ディケードなど)はサンプリング周波数よりもはるかに低い周波数でのみ機能します。 私たちの場合、サンプリング周波数の半分に近い領域でLACHを検討しますが、アナログの世界の法則は機能しません。
したがって、位相特性のタイプにより、このリンクは5次リンクであると結論付けることができます。
フィルターのタイプ。 LACHの形式(LACHの通過帯域では、可能な限り平坦)とGVZグラフの形式(カットオフ周波数付近の極値)を考慮すると、このリンクはバターワースフィルターであると想定できます。 仮定を確認するために、双線形変換法[ Wikipedia ]によって合成されたカットオフ周波数0.25の理想的なバターワースデジタルフィルターのLACH、PFC、およびGVZを構築します。
グラフでは、赤い実線は調査中のフィルターに対応する値を示し、青い点線は双線形変換法によって合成された理想的なバターワースデジタルフィルターを示します。



グラフからわかるように、調査したフィルターのパラメーターと、バイリニア変換法によって合成された理想的なバターワースデジタルフィルターのパラメーターがほぼ完全に一致しています。
おわりに
この論文では、注目に値する5次のバターワースデジタルフィルターの実装を検討しました。 フィルターのこの実装は、制限サイクルという形での欠点にもかかわらず、大きな尊敬に値します。 テキサス・インスツルメンツのエンジニアは、乗算と除算の操作を使用することなく、かなり洗練された5次フィルターアルゴリズムを整数で実装することができました。
あなたの謙虚な使用人は、この論文で使用されるデジタルフィルターコード分析方法が読者にとって興味深く有用であることを心から望んでいます。