RandLibライブラリを使用すると、50を超える有名な分布、連続、離散、2次元、周期的、さらには1つの特異な分布を扱うことができます 。 何らかの配布が必要な場合は、その名前を入力し、接尾辞Randを追加します。 に興味がありますか?
ランダムジェネレーター
標準C ++テンプレートライブラリを使用して正規分布から100万のランダム変数を生成する場合、次のように記述します。
std::random_device rd; std::mt19937 gen(rd()); std::normal_distribution<> X(0, 1); std::vector<double> data(1e6); for (double &var : data) var = X(gen);
あまり直感的ではない6行。 RandLibでは、その数を半分にすることができます。
NormalRand X(0, 1); std::vector<double> data(1e6); X.Sample(data);
1つのランダムな標準正規分布数量のみが必要な場合、これは1行で実行できます。
double var = NormalRand::StandardVariate();
ご覧のとおり、RandLibは2つのことからユーザーを救います:ベースジェネレーター(0から特定のRAND_MAXまでの整数を返す関数)の選択と、ランダムシーケンスの開始位置の選択(srand()関数)。 多くのユーザーはこの選択を必要としない可能性が高いため、これは便利な名前で行われます。 ほとんどの場合、ランダム値はベースジェネレーターから直接生成されるのではなく、このベースジェネレーターに既に依存している0から1に均等に分布するランダム値Uを通じて生成されます。 Uの生成方法を変更するには、次のディレクティブを使用する必要があります。
#define UNIDBLRAND // #define JLKISS64RAND // 64- #define UNICLOSEDRAND // U 0 1 #define UNIHALFCLOSEDRAND // U 0, 1
デフォルトでは、Uは0も1も返しません。
発生率
次の表は、1つのランダム変数をマイクロ秒単位で生成する時間の比較を示しています。
システム仕様
Ubuntu 16.04 LTS
プロセッサー:Intel Core i7-4710MQ CPU @ 2.50GHz×8
OSタイプ:64ビット
プロセッサー:Intel Core i7-4710MQ CPU @ 2.50GHz×8
OSタイプ:64ビット
| 配布 | STL | ランドリブ |
|---|---|---|
|
| 0.017μs | 0.006μs |
|
| 0.075μs | 0.018μs |
|
| 0.109μs | 0.016μs |
|
| 0.122μs | 0.024μs |
|
| 0.158μs | 0.101μs |
|
| 0.108μs | 0.019μs |
その他の比較
| ガンマ分布: | ||
|---|---|---|
|
| 0.207μs | 0.09μs |
|
| 0.161μs | 0.016μs |
|
| 0.159μs | 0.032μs |
|
| 0.159μs | 0.03μs |
|
| 0.159μs | 0.082μs |
| 学生の分布: | ||
|
| 0.248μs | 0.107μs |
|
| 0.262μs | 0.024μs |
|
| 0.33μs | 0.107μs |
|
| 0.236μs | 0.039μs |
|
| 0.233μs | 0.108μs |
| フィッシャー分布: | ||
|
| 0.361μs | 0.099μs |
|
| 0.319μs | 0.013μs |
|
| 0.314μs | 0.027μs |
|
| 0.331μs | 0.169μs |
|
| 0.333μs | 0.177μs |
| 二項分布: | ||
|
| 0.655μs | 0.033μs |
|
| 0.444μs | 0.093μs |
|
| 0.873μs | 0.197μs |
| ポアソン分布: | ||
|
| 0.048μs | 0.015μs |
|
| 0.446μs | 0.105μs |
| 負の二項分布: | ||
|
| 0.297μs | 0.019μs |
|
| 0.587μs | 0.257μs |
|
| 1.017μs | 0.108μs |
ご覧のとおり、RandLibはSTLの1.5倍の速さで、2、10の場合もありますが、決して遅くはありません。 RandLibで実装されたアルゴリズムの例は、 こことここで見ることができます 。
分布関数、モーメント、およびその他のプロパティ
ジェネレーターに加えて、RandLibはこれらの分布の確率関数を計算する機能を提供します。 たとえば、パラメーターaのポアソン分布を持つ確率変数が値kをとる確率を見つけるには、関数Pを呼び出す必要があります。
int a = 5, k = 1; PoissonRand X(a); XP(k); // 0.0336897
そのため、離散分布の値を取る確率を返す関数を指定するのは大文字のPでした。 連続分布の場合、この確率はほぼすべてゼロであるため、代わりに文字fで示される密度を考慮します。 連続分布と離散分布の両方の分布関数を計算するには、関数Fを呼び出す必要があります。
double x = 0; NormalRand X(0, 1); Xf(x); // 0.398942 XF(x); // 0
関数1-F(x)を計算する必要がある場合があります。F(x)は非常に小さな値を取ります。 この場合、精度を失わないために、関数S(x)を呼び出す必要があります。
値のセット全体の確率を計算する必要がある場合は、関数を呼び出す必要があります。
//x y - std::vector X.CumulativeDistributionFunction(x, y); // y = F(x) X.SurvivalFunction(x, y); // y = S(x) X.ProbabilityDensityFunction(x, y) // y = f(x) - X.ProbabilityMassFunction(x, y) // y = P(x) -
分位数は、p = F(x)となるxを返すpの関数です。 対応する実装は、1次元分布に対応する各有限RandLibクラスにもあります。
X.Quantile(p); // x = F^(-1)(p) X.Quantile1m(p); // x = S^(-1)(p) X.QuantileFunction(x, y) // y = F^(-1)(x) X.QuantileFunction1m(x, y) // y = S^(-1)(x)
関数f(x)またはP(k)の代わりに、対応する対数を取得する必要がある場合があります。 この場合、次の機能を使用するのが最適です。
X.logf(k); // x = log(f(k)) X.logP(k); // x = log(P(k)) X.LogProbabilityDensityFunction(x, y) // y = logf(x) - X.LogProbabilityMassFunction(x, y) // y = logP(x) -
RandLibは、特性関数を計算する機能も提供します。
X.CF(t); // \phi(t) X.CharacteristicFunction(x, y) // y = \phi(x)
さらに、最初の4つのポイントまたは期待値、分散、非対称係数、尖度を簡単に取得できます。 さらに、中央値(F ^(-1)(0.5))およびモード(fまたはPが最大値をとるポイント)。
LogNormalRand X(1, 1); std::cout << " Mean = " << X.Mean() << " and Variance = " << X.Variance() << "\n Median = " << X.Median() << " and Mode = " << X.Mode() << "\n Skewness = " << X.Skewness() << " and Excess kurtosis = " << X.ExcessKurtosis();
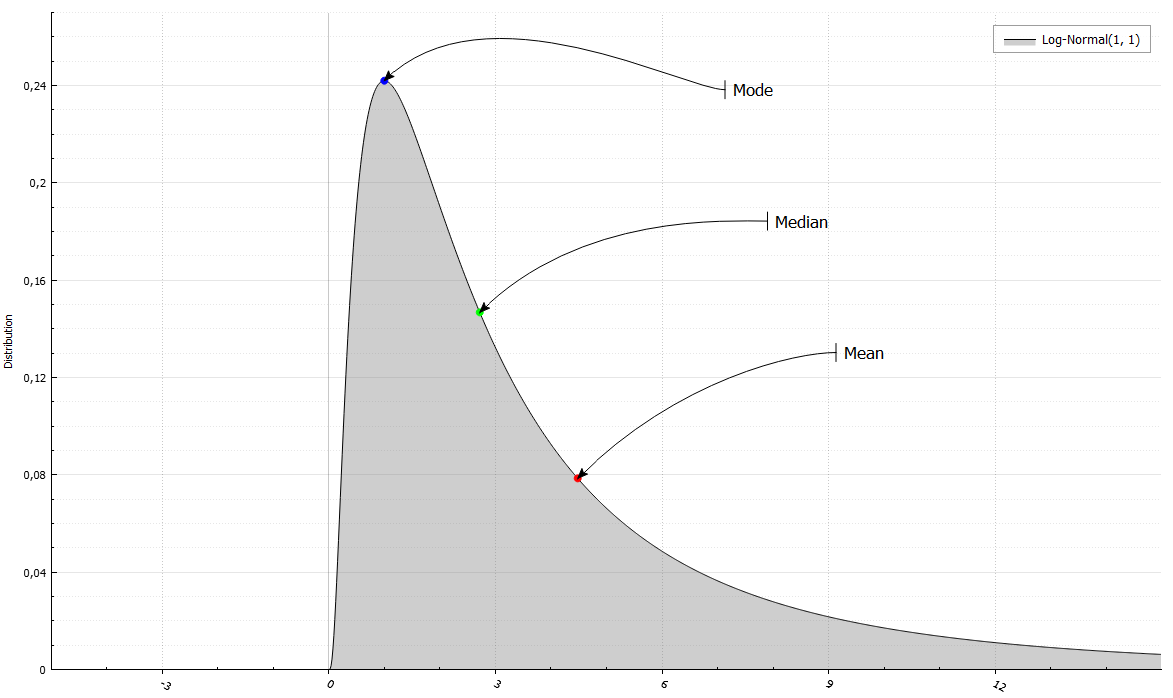
Mean = 4.48169 and Variance = 34.5126 Median = 2.71828 and Mode = 1 Skewness = 6.18488 and Excess Kurtosis = 110.936
パラメータ推定と統計的検定
確率論から統計まで。 一部の(まだすべてではない)クラスには、推定値に対応するパラメーターを設定するFit関数があります。 正規分布の例を考えてみましょう。
using std::cout; NormalRand X(0, 1); std::vector<double> data(10); X.Sample(data); cout << "True distribution: " << X.Name() << "\n"; cout << "Sample: "; for (double var : data) cout << var << " ";
標準正規分布から10個の要素を生成しました。 出力は次のようになります。
True distribution: Normal(0, 1) Sample: -0.328154 0.709122 -0.607214 1.11472 -1.23726 -0.123584 0.59374 -1.20573 -0.397376 -1.63173
この場合のFit関数は、最尤推定に対応するパラメーターを設定します。
X.Fit(data); cout << "Maximum-likelihood estimator: " << X.Name(); // Normal(-0.3113, 0.7425)
既知のように、正規分布の分散の最尤は、偏った推定値を与えます。 したがって、Fit関数には追加の不偏パラメータ(デフォルトではfalse)があり、これを使用して推定値のバイアス/非バイアスを調整できます。
X.Fit(data, true); cout << "UMVU estimator: " << X.Name(); // Normal(-0.3113, 0.825)
ベイジアンイデオロギーのファンのために、ベイジアン評価もあります。 RandLib構造により、アプリオリ分布と事後分布での操作が非常に便利になります。
NormalInverseGammaRand prior(0, 1, 1, 1); NormalInverseGammaRand posterior = X.FitBayes(data, prior); cout << "Bayesian estimator: " << X.Name(); // Normal(-0.2830, 0.9513) cout << "(Posterior distribution: " << posterior.Name() << ")"; // Normal-Inverse-Gamma(-0.2830, 11, 6, 4.756)
テスト
分布関数のようなジェネレーターが正しい値を返すことをどのように知っていますか? 回答:互いに比較してください。 連続分布の場合、対応する分布のこのサンプルのメンバーシップについてコルモゴロフ-スミルノフ検定を実行する関数が実装されます。 KolmogorovSmirnovTest関数は、序数統計と入力として\ alphaレベルを受け入れ、選択が分布と一致する場合にtrueを返します。 離散分布は、PearsonChiSquaredTest関数に対応しています。
おわりに
この記事は、特にhabrasocietyの一部のために書かれており、これに興味があり、感謝することができます。 理解して、突っついて、健康を使いましょう。 主な利点:
- 無料
- オープンソース
- 作業速度
- 使いやすさ(私の主観的な意見)
- 依存関係なし(はい、何も必要ありません)
リリースへのリンク。