PyMC3-MSMSなど

こんにちは、Habrahabr!
この投稿では、PyMC3について既に言及しています。 ここで、MCMCサンプリングの基本について読むことができます。 ここでは、変分推論( ADVI )、これがすべて必要な理由について説明し、PyMC3ギャラリーのかなり簡単な例でこれがどのように役立つかを示します。 そのような例の1つは、分類問題のベイジアンニューラルネットワークですが、これは最後です。 誰も気にしない-ようこそ!
はじめに
主要部分に移る前に、ベイジアン分析の用語を更新する必要があると考えます。 この確率論のサブセクションの主題は、事後分布の導出です。 タスクは次のとおりです。
アナリストは、観測不可能な(潜在的な)モデルパラメーターについて何かを学びたい z そして彼は彼らが何であるかについていくつかの考えを持っています p(z) 。 さらに、彼は自分のデータがどれだけうまく判断できるか D パラメーターを使用してモデルに適合 z 。 これは信頼性によって表されます。 p(D|z) -指定されたパラメーターでデータを観測する確率。
\大p(z|D)= fracp(z、D)p(D)= fracp(D|z)p(z)p(D)
どこで
p(z) -先験的な分布、期待される結果に関する仮定。
問題の解決に近づくと、非常に多くの場合、調査されている現象のアイデアがあります。
- たとえば、物理学の分野を取り上げます。 相互作用の法則とメカニズムがありますが、それらについては良い考えがあります(たとえば、表面と物質の摩擦係数などの量を除いて)。 過去の経験と蓄積された知識に基づいて、それがどうあるべきかをおおまかに仮定します。 少なくともゼロよりも大きいという事実。 評価したい未知のパラメータを使用して物理モデルを構築することにより、実験を構築できます。
- 重要な注意:観測データにアプリオリ分布を調整したい場合があります。 たとえば、求めているデータを推定したとしましょう z どこかに 3 事後表示を開始します。 待ってください。しかし、たとえば定理を証明するとき、その結果を使ってそれを証明しませんか? また、ここで、アプリオリ分布は研究対象のデータセットに基づくべきではありません。
- p(D|z) -可能性、容疑者の妥当性の評価 z 。 これは、選択された仮説の対象となるデータを観測する確率で表されます z 。
- 実験結果があり、パラメーターの各セットについて、「モデルが世界をどの程度うまく記述しているか」を評価できます。 この考え方は、MLE評価の古典的な統計で使用されます。
- p(z|D) -事後分布、取得したい結論。
- 実際、これらは、実験中に開発したモデルの未知のパラメーター(摩擦係数)に関するアイデアです。 これは、古い知識と新しい知識の間の妥協と見なすことができます。 p(z) そして p(D|z) それに応じて。
- p(D) -証拠、一般的にそのようなデータを取得する確率はロシア語にひどく翻訳されています。
ベイズの結論
一見、特別なものはありません:密度公式があります p(D|z) 、 p(z) 、目的の密度は次のとおりです。
largep(z|D)= fracp(D|z)p(z)p(D)= fracp(D|z)p(z) intp(D|z)p(z)dz
2つの密度を乗算しても問題はありません。 以下の積分を計算するには?..うーん、まあ、あなたは大学の分析のコースを思い出すことができます...一般的に、我々は式のすべてを置き換えて、あなたは完了です。 この知識があれば、安全に単純な分布の単純なモデルを探索できます。 しかし、ほぼ実例に近い場合、そのような知識でさえ保存されず、分析的に積分を取ることはできません。
なんでこんなこと?
まあ、分布を推測することはできないので p(z|D) 、なぜ分布密度が最大であるかなど、単純なポイント推定値に限定しないのはなぜですか? まあ、または最後の手段として、これを行って最大値を探すことさえしないでください p(D|z) 、それでもデータを説明するモデルを構築したいと考えています。 最初のアプローチはMAP (最大事後)評価と呼ばれます zmap=argmaxzp(z|D) 2番目はML (最尤法)です zml=argmaxzp(D|z) 。 2番目の方法は、工科大学のほぼすべての学生が確率論のコースを受講したことです。
ML評価には多くの欠点があります。 それらの中で最も直感的なのは、この基準の観点からは複雑なモデルでさえ魅力的に見えるかもしれないということです。 確かに、確率が大きいほど良いですが、パラメーターが増えると、モデルは単純にデータを繰り返すことができます。 この事実は誤解を招くものであり、モデルが適切である理由を正当化せざるを得ません。 ベイジアン推論の観点から、MAPのようなML推定を想像できます。 p(z)=均一[− infty、 infty] 。 はい、積分は行われませんが、ポイント推定値があり、これは私たちを傷つけません、密度を考慮します p(z) 定数。
証明
largep(z|D)= fracp(z、D)p(D)= fracp(D|z)p(z)p(D)\右矢印max
large logp(z|D)= log fracp(z、D)p(D)= log fracp(D|z)p(z)p(D)\右矢印max
large sim logp(D|z)p(z)− logp(D)\右矢印max
large sim logp(D|z)+ logp(z)\右矢印max
large sim logp(D|z)\右矢印max
このような事前分布は、 不適切な事前分布と呼ばれ、具体的には情報価値のない(情報価値のない)ものです。
言い換えれば、私たちは何をすべきかわからない z 実際に。 利用可能なすべての情報を使用する機能は失われます。 例:
- 理論からのいくつかの問題について、それは確実に知られています z 厳密にゼロより大きい。 これは変換によって修正できますが、設定を「ゼロ未満」に変更すると、MLはこれを考慮できなくなります。
- 線形回帰の場合、多数の回帰変数が存在する場合、それらすべてが重要であるとは考えられていません。 次にベクトルで z (係数)多くのゼロ成分があります。
標準的なアプローチは、その実装の単純さと研究された漸近特性のために優れていますが、MAPは多くの状況でより意味があります。
from theano import theano, tensor as tt import pymc3 as pm import pandas as pd from sklearn import datasets import numpy as np from numpy import random import pylab as plt import seaborn as sns import warnings import scipy.stats as stats warnings.filterwarnings('ignore') %matplotlib inline plt.mpl.style.use('ggplot')
コインの例
新しい観測を取得したときに事後分布がどうなるかを見てみましょう。 これは、最も一般的な意味での自信の変化に非常に似ています。 最初は何も知りませんが、例を得ると、観測できない要因の考え方が変わります。 明確な表現のために、事後分布の正直な結論を使用します。
事前に 均一[0、1] (に等しい Beta[ alpha=1、 beta=1] )「ワシ」を得る確率 r ワシの観察 t と尾 f 合計 N 観測、確率の事後分布を取得します Beta[ alpha=t+1、 beta=f+1] 。
largep(r|T=t、F=f)= fracp(T=t、F=f|r)p(r) intp(T=t、F=f|r)p(r)dr
large= fracCkNrt(1−r)f int10CkNrt(1−r)fdf= fracrt(1−r)fB(t+1、f+1)
large=Beta(r| alpha=t+1、 beta=f+1)
説明のために、いくつかの補助機能と合成データが必要です。
# def posterior(t, f): """ t : f : """ return stats.beta(a=t+1, b=f+1) # def plot_pdf(dist, ax, c): space = np.linspace(0, 1) pdf = dist.pdf(space) ax.plot(space, pdf, c=c, alpha=.5) return ax
# true_p = .3 # "" random.seed(42) # trials = np.random.uniform(size=100) < true_p # , 1 # [t, f] observed = np.array(list(zip(np.cumsum(trials), np.arange(1, trials.size+1) - np.cumsum(trials)))) observed[:6]
array([[0, 1], [0, 2], [0, 3], [0, 4], [1, 4], [2, 4]])
fig, ax = plt.subplots(figsize=(15, 5)) cmap = plt.get_cmap('cool') plot_pdf(posterior(0, 0), ax, cmap(0)) for (t, f), c in zip(observed, np.linspace(0, 1, num=observed.shape[0])): plot_pdf(posterior(t, f), ax, cmap(c)) plt.title(' ') plt.show()

例が多いほど、事後分布が狭くなり、これは新しい知識に対する信頼の現れです。 さらに興味深いのは、少数の観測による分布の振る舞いです。不確実性を適切に反映しています。 これは、古典的な統計の方法を使用してMLE推定値を探す場合には起こりません。 少数の観測でワシの確率は0になりますが、もちろんそうではありません。
やる気
PyMC3では、式を直接導出せずに事後分布を導出できます。 これにより、ほぼすべての適切なモデルでベイジアン確率的推論が可能になります。 さらに、その助けにより、パラメータの代わりに分布、したがって予測も分布である確率的ニューラルネットワークを構築することが可能です。

PyMC3の使用開始
PyMC3ライブラリは Theanoの上に記述されているため、使用できます。 Theanoはテンソル代数のライブラリであり、深層学習に広く使用されています。 シンボリック操作と微分をサポートしているため、 backpropを使用してニューラルネットワークをトレーニングできるだけでなく、変分ベイズの導出も可能です。
PyMC3での作業の大部分は、 Theanoでの作業に似ています。以前の投稿の 1つで、 PyMC3についてよく書かれています。
ライブラリの基本部分はモデル( pm.Model
)であり、その場で事後密度(より正確には、非正規化部分)を構成できます。 これが素晴らしいインターフェイスで動作するために、コンテキストマネージャで少し魔法が適用されます。 PyMC3の潜在変数はwith model: ...
内のコンテキスト内で宣言されますwith model: ...
潜在変数自体は、 Theano
の意味での変数です;それらについては、 Theano
通常のテンソルに当てはまるすべてが当てはまります。 これは、より複雑なモデルを実験して構築することを恐れないように覚えておくと便利です。
モデルの複雑さを増すとMCMCメソッドが結果を低下させるか、少なくとも法外に遅くなる可能性があることを実例で示すために、モデルを順次構築します。
pm.sample
ヘルパー関数を使用してpm.sample
をpm.sample
できます。これはデフォルトの設定で問題なく機能しますが、デモ用に変更されています。 デフォルトでは、MCMCメソッド用に適切なパラメーターが事前に選択されていますが、これは現在では必要ありません。
# import pymc3 as pm with pm.Model() as simple_model: # # norm = pm.Normal('norm', 0, 1) # MCMC NUTS step = pm.NUTS() trace = pm.sample(1000, step=step) # :
WARNING (theano.tensor.blas): We did not found a dynamic library into the library_dir of the library we use for blas. If you use ATLAS, make sure to compile it with dynamics library. 100%|██████████| 1000/1000 [00:00<00:00, 1368.27it/s]
トレースプロット
結果を視覚化するための優れたユーティリティがあります。 たとえば、 TracePlot 。 これはマルコフ連鎖の歴史のグラフです。 分析することにより、アルゴリズムがどの程度うまく機能したか、追加の構成が必要かどうかを理解できます。 視覚的な品質基準は次のとおりです。
- 定常性。 サンプルは値の周りにノイズを生成するはずです。
- それらには顕著な自己相関はありません。 これは予想されることもありますが(下記を参照)、それを持たないほうが良い
- ストーリー全体が同じ繰り返しのポイントから立つことはできません。 一部の変数が一定のままである場合、おそらくモデル自体のコードに何か問題がありました。
pm.traceplot(trace);

モデルを少し複雑にしましょう
with pm.Model() as simple_model: norm = pm.Normal('norm', 0, 1) # laplace = pm.Laplace('lap', mu=norm, b=3) step = pm.NUTS() trace = pm.sample(1000, step=step)
100%|██████████| 1000/1000 [00:36<00:00, 27.10it/s]
正規分布のマルコフ連鎖の乱流が顕著になりました。
pm.traceplot(trace);
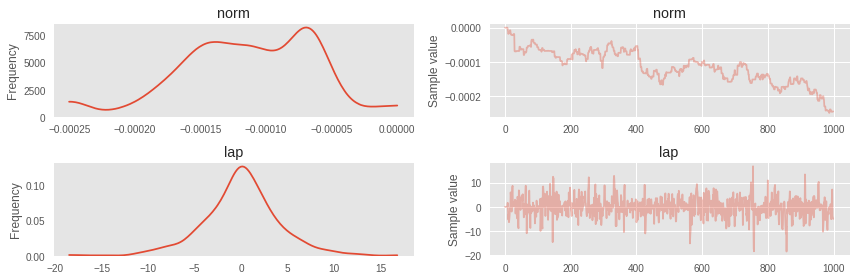
これは、独立した正規分布の最初の変数を使用する必要がありましたが、モデルが自明ではなくなったときに発生します。 そのような場合、まずADVIを不明瞭にして、そこからの共分散行列と平均を使用してNUTSを初期化できます。 しかし、まず、ADVIについて詳しく説明します。
ADVI
ADVIは自動微分変分推論 ( 記事リンク )の略です。 これはおそらく、おおよそのベイジアン出力に最も簡単で最も一般的に使用されるアルゴリズムの1つです。 潜在空間の次元が大きくなると、MCMCメソッドの構成が非常に難しくなる(デフォルトのパラメーターは適切ではない)か、反復に膨大な時間がかかります。 デフォルトのパラメーターが機能しない可能性があるという事実は、上記で確信しました。 そして、少なくとも、ターゲットとなるディストリビューションを、私たちが協力できるディストリビューションに近づける必要が生じます。
理論
この方法の本質は、事後分布を近似することです p(z|D) その他の配布 q(z) 、密度とサンプルをカウントできます。 古典的な設定では、そのような分布は対角共分散行列を持つ多次元正規分布です mathcalN( bar0、diag( bar sigma2)) 。 これが主な欠点です。潜在変数が独立しているという仮定が立てられますが、もちろんこれは必ずしもそうではありません。 それにもかかわらず、そのような強い前提があっても、良い結果を達成することができます。 さらに、このような単純化によってコンピューティングリソースがどのように節約されるかを確認します。
問題の声明
観察してみましょう mathcalD 、パラメータ付きのパラメトリックモデル z in mathcalRn およびその尤度関数 p(D|z) 。 さらに、ベイジアンアプローチでは、モデルパラメーターのアプリオリ分布が必要です。 p(z) 。 ベイズ規則に従って、パラメーターの事後分布を導き出します。
\大p(z|D)= fracp(D|z)p(z) intp(D|z)p(z)dz
通常、正規化定数なしで部品を計算することは難しくありません。
\大p(z|D) proptop(D|z)p(z)
分布のパラメトリックファミリを定義します q theta inQ 誰と一緒に働きますか。
メトリック。 分布空間でのメトリックの標準的な選択は、Kullback-Leibler距離です
\大きいKL(q||p)= mathbbEq(z)[logq(z)−logp(z|D)]
分布が一致する場合、期待値はゼロです。それ以外の場合、期待値はゼロより大きくなります。 したがって、ベイジアン推論問題は最適化問題に還元されます
largeq theta∗= undersetq theta inQargminKL(q theta||p)
問題解決
この問題は、確率的勾配降下法によって解決されます。 これを行うには、に関する微分を取ります \シータ 。
large mathbbEq theta(z)[logq theta(z)−logp(z|D)]
large= mathbbEq theta(z)[logq theta(z)]− mathbbEq theta(z)[logp(z|D)]
large= mathbbEq theta(z)[logq theta(z)]− mathbbEq theta(z)[logp(D|z)]− mathbbEq theta(z)[logp(z)]+ mathbbEq theta(z)[logp(D)]
KLメトリックを完全に分解しました。最小化する必要があるため、 mathbbEq theta(z)[logp(D)] すべて同じ定数である場合、考慮する必要はありません。 そこで、事後分布の分析的導出の主な問題である非傾斜積分を取り除きます。 残っているのは等しい $インライン$ -ELBO $インライン$ ( 証拠下限 )。
すべてがさらに分析的に設定され、十分に考慮されているように見えますが、1つあります。 パラメーターに関する微分をとるには、積分に関する微分をとる必要があり、積分はこれらの同じパラメーターに依存します。 MCメソッドを使用してこれを実行し、いくつかのサンプルで積分を近似すると、勾配の分散が大きいという事実に遭遇します。 これは回避でき、選択した事後分布のファミリーによりこれが可能になります。 以下の定理は、積分の符号の下で導関数を導入できる場合の条件を示しています。
定理
させる \イプシロン 分布密度を持つランダム変数 q(\イプシロン) そしてみましょう z=t(\シータ、\イプシロン) どこで t -決定論的可逆関数。 ランダム変数の分布密度を z それは q(z|\シータ) 。 さらに、 q( epsilon)d epsilon=q(z| theta)dz 。
次に、関数 f 派生物 z やった
large frac partial partial theta mathbbEq(z| theta)[f(z、 theta)]= mathbbEq( epsilon)[ frac partialf(z、 theta) partialz frac partialz partial theta+ fracf(z、 theta) partial theta]
これは最適化に必要です。 以来 z sim mathcalN( mu、exp(w)2) として表すことができます z=t( mu、w、 epsilon)= epsilon∗exp(w)+ mu どこで epsilon sim mathcalN(0、1) 。 させる theta=( mu、w)
これはReparametrization Trickと呼ばれます。 それを使用すると、派生物を取得するのがはるかに簡単です ELBO 。
large− nablaELBO= mathbbE mathcalN(0、1)[ nabla thetalogq theta(t( theta、 epsilon))− nabla thetalogp(D|t( theta、 epsilon))− nabla thetalogp(t( theta、 epsilon))]
適切な再パラメータ化を行ったら、式でtheano.grad
を呼び出して、勾配を高くするか、むしろその唯一のサンプルを取得するだけで十分です。 その後、お気に入りのオプティマイザーを使用できます。
with pm.Model() as simple_model: norm = pm.Normal('norm', 0, 1) laplace = pm.Laplace('lap', mu=norm, b=3) trace = pm.sample(1000, init='advi', n_init=10000)
Auto-assigning NUTS sampler... Initializing NUTS using advi... Average ELBO = -0.11837: 100%|██████████| 10000/10000 [00:00<00:00, 13764.87it/s] Finished [100%]: Average ELBO = -0.1085 Evidence of divergence detected, inspect ELBO. 100%|██████████| 1000/1000 [00:01<00:00, 974.36it/s]
すでにはるかに優れています。
ヒント:トランスプロットでは、マルコフ連鎖を確認することが重要です。理想的には、ここのように静止している必要があり、上記のように乱流ではありません
pm.traceplot(trace);

with pm.Model() as simple_model: norm = pm.Normal('norm', 0, 1) laplace = pm.Laplace('lap', mu=norm, b=3) # ( ) lognorm = pm.Lognormal('lognorm', sd=norm**2 + 1e-7, testval=1) trace = pm.sample(10000, n_init=40000)
Auto-assigning NUTS sampler... Initializing NUTS using advi... Average ELBO = -7.4197e+05: 100%|██████████| 40000/40000 [00:03<00:00, 11614.15it/s] Finished [100%]: Average ELBO = -1.221e+08 Evidence of divergence detected, inspect ELBO. 100%|██████████| 10000/10000 [01:06<00:00, 150.87it/s]
最初のマルコフ連鎖には顕著な自己相関があることがわかります。 実際、標準偏差として正規分布の2乗を使用したという事実により、NUTSは局所密度の最大値でスタックしているため、驚くことではありません。
# 100 pm.traceplot(trace[100:]);

モデルは順番に構成することができ、オプションで1つのコンテキストで即座に構成できます。
random.seed(42) obs = random.normal(0, 1, size=10) + random.normal(0, 10, size=10) with pm.Model() as model: hc = pm.HalfCauchy('hc', beta=1) # your code with model: # , norm = pm.Normal('norm', 0, hc, observed=obs) with model: trace = pm.sample(1000, tune=200, n_init=1000) pm.traceplot(trace[10:]);
Auto-assigning NUTS sampler... Initializing NUTS using advi... Average ELBO = -1,954.7: 100%|██████████| 1000/1000 [00:00<00:00, 8967.46it/s] Finished [100%]: Average ELBO = -1,402.2 100%|██████████| 1000/1000 [00:00<00:00, 1464.22it/s]

PyMC3のイデオロギーは、構築中にモデルの有効性をチェックすることを提供します。これにより、エラーは初期段階で回避されます。 これはtest_value
を強制することで実現されtest_value
norm.tag.test_value
array([ -4.13746262, -4.79556179, 3.06731129, -17.60977173, -17.48333168, -5.85701227, -8.54909801, 3.90990806, -9.54971504, -13.58047676], dtype=float32)
Theano
、ベクトル化された操作に最適です。 したがって、モデルの設定方法(ループまたは風のランダム変数の作成)を選択する必要がある場合は、2番目のオプションを選択することをお勧めします。 この場合、独立したランダム変数が作成され、後でインデックスによってアクセスできます。
with pm.Model() as model: vectorized_p = pm.Uniform('p', shape=(4,)) vectorized_p.tag.test_value
array([ 0.5, 0.5, 0.5, 0.5], dtype=float32)
デフォルトの初期化が気に入らない場合は、独自の初期化を指定できます。
with pm.Model() as model: vectorized_p = pm.Uniform('p', shape=(4,), testval=np.ones((4,), 'float64') * .3, dtype='float64') vectorized_p.tag.test_value
array([ 0.3, 0.3, 0.3, 0.3])
ベイジアン線形回帰
最初の多かれ少なかれ意味のある例は、ボストンのアパートの価格についてです。
data_ = datasets.load_boston() data = pd.DataFrame(data=data_['data'], columns=data_['feature_names']) y = data_['target']
print('\n'.join(data_.DESCR.splitlines()[13:28]))
:Attribute Information (in order): - CRIM per capita crime rate by town - ZN proportion of residential land zoned for lots over 25,000 sq.ft. - INDUS proportion of non-retail business acres per town - CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) - NOX nitric oxides concentration (parts per 10 million) - RM average number of rooms per dwelling - AGE proportion of owner-occupied units built prior to 1940 - DIS weighted distances to five Boston employment centres - RAD index of accessibility to radial highways - TAX full-value property-tax rate per $10,000 - PTRATIO pupil-teacher ratio by town - B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town - LSTAT % lower status of the population - MEDV Median value of owner-occupied homes in $1000's
data.head()
| クリム | Zn | インダス | チャス | NOX | RM | 年齢 | DIS | RAD | 税 | PTRATIO | B | Lstat | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
単純なベイズ線形モデルを作成します。
PRICE simCRIM+ZN+INDUS+CHAS+NOX+RM+AGE+DIS+RAD+TAX+PTRATIO+B+LSTAT
デフォルトでは、係数のPriorはNormal(mu=0, tau=1.0E-6)
で、定数の場合はFlat
です。
変更についてSVGDを使用してモデルを評価します。
from functools import partial with pm.Model() as lm_model: lm_model = pm.GLM(x=data, y=y) # pm.fit histogram = pm.fit(200, method='svgd', obj_optimizer=partial(pm.adagrad, learning_rate=.7))
100%|██████████| 200/200 [00:05<00:00, 35.31it/s]
そして、私たちはディストリビューションを得ました! これから信頼区間を構築することが可能になりました。これを回帰変数の係数に対して行います。
# `histogram.sample` , pm.sample. # pm.forestplot(histogram.sample(300), varnames=data.columns);

ベイジアンニューラルネットワーク

PyMC3
バックエンドはTheano
であるため、ニューラルネットワークにベイジアン変分出力を使用することは完全に自然な願いです。 これは、 Lasagne
を使用して非常に簡単かつ透過的に取得できます。
ベイジアンニューラルネットワークの通常の特徴とは異なる特徴は、重みのモデル化方法です。 通常、特定の値は重みとして取得され、勾配降下を使用して最適化されます。
ベイジアンニューラルネットワークの場合、すべてが異なります。 ネットワークの重みは、先験的な分布を持つ観測不能なランダム変数として認識されます。 理想的には、彼らは正直なベイジアンの結論を出す必要がありますが、サンプリングは最も単純なタスクでも遅くなりますが、ここではまったく異なるレベルです。 ベイジアンネットワークをトレーニングする際の一般的な方法は、この分布自体の近似的な変分微分です。 最速の変分法は前述のADVIです。 ここで使用します。
from lasagne.layers import * import lasagne from sklearn import datasets from sklearn.preprocessing import scale from sklearn.cross_validation import train_test_split from sklearn.datasets import make_moons
sklearn
ユーティリティを使用して合成データを生成します
X, Y = make_moons(noise=0.2, random_state=0, n_samples=1000) X = scale(X) # , X Y float64 X = X.astype(theano.config.floatX) Y = Y.astype(theano.config.floatX) X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.5)
fig, ax = plt.subplots() ax.scatter(X[Y==0, 0], X[Y==0, 1], color='b', label='Class 0') ax.scatter(X[Y==1, 0], X[Y==1, 1], color='r', label='Class 1') sns.despine(); ax.legend() ax.set(xlabel='X', ylabel='Y', title='Toy binary classification data set');

Lasagne
では、 Lasagne
文字変数を返す関数を初期化として渡すことができます。 初期化はPyMC3
とは大きく異なるため、独自のアダプターを作成する必要があります。
import itertools class RandomWeight(object): counter = itertools.count(0) def __init__(self, mu=0, sd=1): self.mu = mu self.sd = sd def __call__(self, shape): name = 'auto_%s' % next(self.counter) return pm.Normal(name, self.mu, self.sd, testval=lasagne.init.GlorotUniform()(shape), shape=shape, dtype=theano.config.floatX)
重みが正しく初期化されるように、モデルのコンテキストでニューラルネットワークを作成する必要があります。
input_var = theano.shared(X_train) out_var = theano.shared(Y_train) with pm.Model() as nnet: inp = InputLayer((None, 2), input_var) # , z = DenseLayer(inp, 5, W=RandomWeight(), b=None, nonlinearity=tt.tanh) z = DenseLayer(z, 5, W=RandomWeight(), b=None, nonlinearity=tt.tanh) p = DenseLayer(z, 1, W=RandomWeight(), b=None, nonlinearity=tt.nnet.sigmoid) # , -p(D|z) pm.Bernoulli('observed', p=get_output(p).flatten(), observed=out_var)
このようなモデルの近似ベイジアン結論は、上記のADVIを使用して実行できます。
with nnet: inference = pm.ADVI() approx = inference.fit(30000)
Average Loss = 132.78: 100%|██████████| 30000/30000 [00:35<00:00, 847.38it/s] Finished [100%]: Average Loss = 132.78
plt.figure(figsize=(12, 6)) plt.plot(inference.hist, alpha=.3) plt.legend() plt.ylabel('-ELBO') plt.xlabel('iteration');
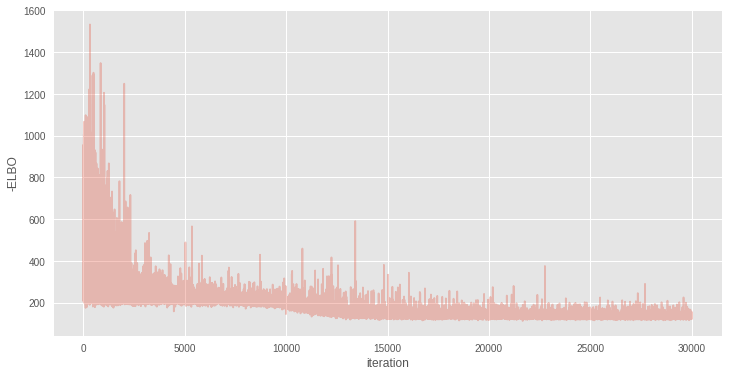
結果を別のタスクに簡単に再利用できます。たとえば、それらを使用して予測を行うことができます。
# x = tt.matrix('X') # n = tt.iscalar('n') # compute_test_value='raise', , x.tag.test_value = np.empty_like(X_train[:10]) n.tag.test_value = 100 # sample_node apply_replacements # pymc3 _sample_proba = approx.sample_node(get_output(p).flatten(), size=n, more_replacements={input_var:x}) # # , sample_proba = theano.function([x, n], _sample_proba)
実際、テストセットで関数を呼び出すことで、予測自体を取得できます。
pred = sample_proba(X_test, 500).mean(0) > 0.5
fig, ax = plt.subplots() ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b') ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r') sns.despine() ax.set(title='Predicted labels in testing set', xlabel='X', ylabel='Y');

境界線を分割する
クラスの境界線を見ることができます。これにより、平面上のすべてのポイントをそこに置き換えて平均化できます。
grid = np.mgrid[-3:3:100j,-3:3:100j].astype('float32') grid_2d = grid.reshape(2, -1).T ppc = sample_proba(grid_2d ,500)
cmap = sns.diverging_palette(250, 12, s=85, l=25, as_cmap=True) fig, ax = plt.subplots(figsize=(16, 9)) contour = ax.contourf(grid[0], grid[1], ppc.mean(axis=0).reshape(100, 100), cmap=cmap) ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b') ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r') cbar = plt.colorbar(contour, ax=ax) _ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y'); cbar.ax.set_ylabel('Posterior predictive mean probability of class label = 0');

信頼モデル
予測におけるモデルの信頼性は非常に興味深いものです。 通常、モデルでは、関心のある値のポイント推定値のみを取得できます。 それだけでは、モデルが周囲の世界をどれだけよく理解しているかについての情報を伝えません。評価の分布だけがこれについて知ることができます。 ベイジアン法を使用して、これは非常に直感的に行われ、さらにPyMC3
かなりうまく実装されていPyMC3
。
cmap = sns.cubehelix_palette(light=1, as_cmap=True) fig, ax = plt.subplots(figsize=(16, 9)) contour = ax.contourf(grid[0], grid[1], ppc.std(axis=0).reshape(100, 100), cmap=cmap) ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b') ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r') cbar = plt.colorbar(contour, ax=ax) _ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y'); cbar.ax.set_ylabel('Uncertainty (posterior predictive standard deviation)');

, PyMC3. , , LDA .
- Bayesian Methods for Hackers
- Weight Uncertainty in Neural Networks
- Automatic Differentiation Variational Inference
- Operator Variational Inference
- Stein Variational Gradient Descent
- jupyter