この記事では、別の方法で説明します。 最も単純な構成から始めましょう。1つのニューロンが1つの入力と1つの出力を持ち、アクティベーションはありません。 次に、ネットワーク構成を小さな反復で複雑にし、それぞれから妥当な最大値を絞り込もうとします。 これにより、文字列でチェーンを引っ張り、ニューラルネットワークアーキテクチャの構築において実際的な直感を得ることができます。これは、実際には非常に貴重な資産であることがわかります。
イラスト素材
分類や回帰などのニューラルネットワークの一般的なアプリケーションは、ネットワーク自体の上のアドオンであり、入力データの準備(符号の選択、データのベクトルへの変換)と結果の解釈という2つの追加ステップが含まれます。 私たちの目的では、これらの追加段階は冗長です。 ネットワークの動作を最も純粋な形で見ているのではなく、ニューラルネットワークが不可欠な部分に過ぎない特定の設計を見ています。
ニューラルネットワークは、多次元関数Rn-> Rnを近似するアプローチに過ぎないことを思い出してください。 人間の知覚の限界を考慮して、この記事では平面上の関数を近似します。 ニューラルネットワークのやや非標準的なアプリケーションですが、その作業を説明する目的には最適です。
枠組み
構成と結果を示すために、Pythonで書かれた人気のあるKerasフレームワークを使用することをお勧めします。 ニューラルネットワークを操作するために他のツールを使用できますが、ほとんどの場合、違いは名前だけです。
最も単純なニューラルネットワーク
ニューラルネットワークの最も単純な可能な構成は、1つの入力と1つの出力がアクティブ化されていない1つのニューロンです(または線形アクティブ化f(x)= xと言えます)。

ご覧のとおり、ネットワーク入力に2つの値が提供されます-xと1。 後者は、オフセットbを導入するために必要です。 すべての一般的なフレームワークでは、入力ユニットはすでに暗黙的に存在し、ユーザーが個別に設定することはありません。 したがって、以下では、1つの値が入力に提供されると想定します。
その単純さにもかかわらず、このアーキテクチャはすでに線形回帰を許可しています。 関数を直線で近似します(多くの場合、標準偏差を最小化します)。 この例は非常に重要なので、できるだけ詳細に解析することを提案します。
import matplotlib.pyplot as plt import numpy as np # -3 3 x = np.linspace(-3, 3, 1000).reshape(-1, 1) # , def f(x): return 2 * x + 5 f = np.vectorize(f) # y = f(x) # , Keras from keras.models import Sequential from keras.layers import Dense def baseline_model(): model = Sequential() model.add(Dense(1, input_dim=1, activation='linear')) model.compile(loss='mean_squared_error', optimizer='sgd') return model # model = baseline_model() model.fit(x, y, nb_epoch=100, verbose = 0) # plt.scatter(x, y, color='black', antialiased=True) plt.plot(x, model.predict(x), color='magenta', linewidth=2, antialiased=True) plt.show() # for layer in model.layers: weights = layer.get_weights() print(weights)
ご覧のとおり、私たちの最も単純なネットワークは、バングのある線形関数で線形関数を近似するタスクに対処しました。 ここで、より複雑な関数を使用してタスクを複雑化してみましょう。
def f(x): return 2 * np.sin(x) + 5
繰り返しますが、結果はかなりまともです。 トレーニング後のモデルの重みを見てみましょう。
[array([[ 0.69066334]], dtype=float32), array([ 4.99893045], dtype=float32)]
最初の数値は重みw、2番目の数値はオフセットbです。 これを確認するために、線f(x)= w * x + bを描画します。
def line(x): w = model.layers[0].get_weights()[0][0][0] b = model.layers[0].get_weights()[1][0] return w * x + b # plt.scatter(x, y, color='black', antialiased=True) plt.plot(x, model.predict(x), color='magenta', linewidth=3, antialiased=True) plt.plot(x, line(x), color='yellow', linewidth=1, antialiased=True) plt.show()
それはすべて一緒に収まります。
例の複雑化
まあ、ラインのアプローチで、すべてが明確です。 しかし、これと古典的な線形回帰はうまくいきました。 近似関数の非線形性のニューラルネットワークをキャプチャする方法
さらに多くのニューロンを投げてみましょう。5個としましょう。 なぜなら 出力に1つの値が期待される場合、ネットワークに別のレイヤーを追加する必要があります。これは、5つのニューロンのそれぞれからのすべての出力値を単純に合計します。
def baseline_model(): model = Sequential() model.add(Dense(5, input_dim=1, activation='linear')) model.add(Dense(1, input_dim=5, activation='linear')) model.compile(loss='mean_squared_error', optimizer='sgd') return model
以下を開始します。
そして...それは何ももたらされませんでした。 重量行列は少し大きくなりましたが、それでも同じ直線です。 問題は、ネットワークのアーキテクチャが線形関数の線形結合になることです。
f(x)= w1 '*(w1 * x + b1)+ ... + w5'(w5 * x + b5)+ b
つまり 再び線形関数です。 ネットワークの動作をより面白くするには、活性化関数ReLU(整流器、f(x)= max(0、x))を内側の層のニューロンに追加します。これにより、ネットワークは線をセグメントに分割できます。
def baseline_model(): model = Sequential() model.add(Dense(5, input_dim=1, activation='relu')) model.add(Dense(1, input_dim=5, activation='linear')) model.compile(loss='mean_squared_error', optimizer='sgd') return model
セグメントの最大数は、内層のニューロンの数と一致します。 ニューロンを追加すると、より正確な近似を取得できます。
より正確に!
すでに優れていますが、目には傷が見えます-曲がり部では、元の関数が直線ではなく、近似が遅れています。
最適化戦略として、かなり一般的な方法-SGD(確率的勾配降下法)を採用しました。 実際には、慣性を備えた改良版(SGDm、m-運動量)がよく使用されます。 これにより、急な曲がりでよりスムーズに回転することができ、アプローチが目で良くなります:
# , Keras from keras.models import Sequential from keras.layers import Dense from keras.optimizers import SGD def baseline_model(): model = Sequential() model.add(Dense(100, input_dim=1, activation='relu')) model.add(Dense(1, input_dim=100, activation='linear')) sgd = SGD(lr=0.01, momentum=0.9, nesterov=True) model.compile(loss='mean_squared_error', optimizer=sgd) return model
さらに複雑になる
サインは最適化のための非常に優れた機能です。 主に、それは広い台地を持っていないため-すなわち。 機能が非常にゆっくりと変化する領域。 さらに、関数自体は非常に均等に変化します。 構成の強度をテストするために、より複雑な機能を使用してみましょう。
def f(x): return x * np.sin(x * 2 * np.pi) if x < 0 else -x * np.sin(x * np.pi) + np.exp(x / 2) - np.exp(0)
ああ、ああ、私たちはすでに私たちの建築の天井に寄りかかっています。
より多くの非線形性を与える!
前の例で使用したReLU(整流器)を、より非線形の双曲線正接に置き換えてみましょう。
def baseline_model(): model = Sequential() model.add(Dense(20, input_dim=1, activation='tanh')) model.add(Dense(1, input_dim=20, activation='linear')) sgd = SGD(lr=0.01, momentum=0.9, nesterov=True) model.compile(loss='mean_squared_error', optimizer=sgd) return model # model = baseline_model() model.fit(x, y, nb_epoch=400, verbose = 0)
重みの初期化は重要です!
ベンドでは近似が良くなりましたが、ネットワークでは関数の一部が見えませんでした。 別のパラメーター、つまり重みの初期分布を試してみましょう。 私たちは「glorot_normal」の実際の一般的な値を使用します(研究者Xavier Glorotの名前で、一部のフレームワークではXAVIERと呼ばれます)。
def baseline_model(): model = Sequential() model.add(Dense(20, input_dim=1, activation='tanh', init='glorot_normal')) model.add(Dense(1, input_dim=20, activation='linear', init='glorot_normal')) sgd = SGD(lr=0.01, momentum=0.9, nesterov=True) model.compile(loss='mean_squared_error', optimizer=sgd) return model
すでに良い。 しかし、「he_normal」(研究者Kaiming Heの名前)を使用すると、さらに快適な結果が得られます。
どのように機能しますか?
少し休憩して、現在の構成がどのように機能するかを見てみましょう。 ネットワークは双曲線正接の線形結合です:
f(x)= w1 '* tanh(w1 * x + b1)+ ... + w5' * tanh(w5 * x + b5)+ b
# def tanh(x, i): w0 = model.layers[0].get_weights() w1 = model.layers[1].get_weights() return w1[0][i][0] * np.tanh(w0[0][0][i] * x + w0[1][i]) + w1[1][0] # plt.scatter(x, y, color='black', antialiased=True) plt.plot(x, model.predict(x), color='magenta', linewidth=2, antialiased=True) # for i in range(0, 10, 1): plt.plot(x, tanh(x, i), color='blue', linewidth=1) plt.show()
この図は、各双曲線正接が小さな責任範囲を捉えており、その小さな範囲で関数を近似しようとしていることを明確に示しています。 その領域の外側では、接線はゼロまたは1に低下し、縦座標に沿ったオフセットを単純に与えます。
留学先
ネットワーク学習の分野以外で何が起こるか見てみましょう。この場合は[-3、3]です。
前の例から明らかなように、研究分野の境界を超えて、すべての双曲線正接は定数になります(厳密に言えば、ゼロまたはユニティに近い)。 ニューラルネットワークは、研究分野の外を見ることができません。選択したアクティベーターによっては、最適化された関数の値を大まかに推定します。 これは、ニューラルネットワークの機能と入力データを設計するときに覚えておく価値があります。
深く行く
これまで、この構成はディープニューラルネットワークの例ではありませんでした。 内層は1つだけでした。 もう1つ追加します。
def baseline_model(): model = Sequential() model.add(Dense(50, input_dim=1, activation='tanh', init='he_normal')) model.add(Dense(50, input_dim=50, activation='tanh', init='he_normal')) model.add(Dense(1, input_dim=50, activation='linear', init='he_normal')) sgd = SGD(lr=0.01, momentum=0.9, nesterov=True) model.compile(loss='mean_squared_error', optimizer=sgd) return model
ネットワークは、横軸に沿った中央および下側の境界付近の問題のある領域でよりよく機能したことがわかります。
1つの内部層での作業の例 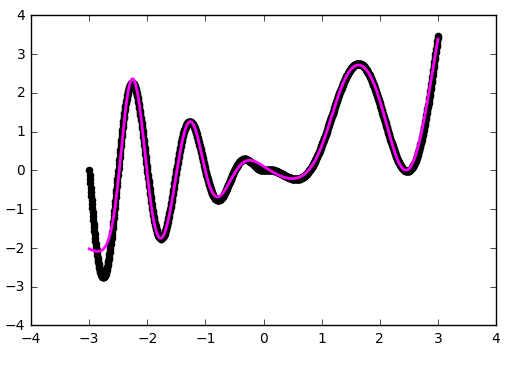
注意レイヤーをブラインドで追加しても、すぐに使用できるものは自動的に改善されません。 ほとんどの実用的なアプリケーションでは、2つの内側のレイヤーで十分であり、フェージンググラデーションの問題など、深すぎるネットワークの特殊効果に対処する必要はありません。 それでも深くすることに決めた場合は、ネットワークの学習で多くのことを試す準備をしてください。
内層のニューロンの数
ちょっとした実験をしてください:
ある瞬間から始めて、内側の層にニューロンを追加しても、最適化は得られません。 良い実用的なルールは、ネットワークの入力と出力の数の間の平均を取ることです。
時代数
結論
ニューラルネットワークは強力ですが、重要なアプリケーションツールです。 実用的なニューラルネットワーク構成を構築する方法を学ぶ最良の方法は、より単純なモデルから始めて、ニューラルネットワークの実践の経験と直感に基づいて多くの実験を行うことです。 そして、もちろん、成功した実験の結果をコミュニティと共有してください。