リポジトリはこちらです。
これに先立ち、サーシャは論文を書きました-「角度係数の行列なしで放射熱伝達の問題を解決する方法」( 論文 、 要約 )。 コードはこちらです。 (VB.NET上にあり、ブレーキがかかりますが、機能し、ドキュメントもあります)
宇宙技術者はモンテカルロ法を使用し、突然それらに気づきました。明らかに、微分方程式系は確率論的です。それらのいくつかはランダムなテストによって得られるからです。
彼らは、可能な限り迅速に微分系を解くアルゴリズムを書きたいので、確率微分方程式の数値解法の分野で専門の数学者の助言が必要です。
彼らは、CUDAでモンテカルロ法を使用して放射線コースを計算するための超並列アルゴリズムを構築することにより、主な問題を解決したようです。 今、彼らは自分のシステムを統合に使用したいと考えています。それは、10万個の未知数の大きな次元であり、時間の経過とともに統合するための堅固で適切な方法です。 従来の明示的な方法は、非常に小さな時間ステップを必要としますが、暗黙的な方法は、右側を計算するのに何回も必要としますが、これはリソースを消費します。
したがって、このような要件の組み合わせに適しており、迅速に計算できる統合方法を見つけるか、構築する必要があります。
それは何のためですか?
現在、ロシアと世界全体では、衛星熱伝達の計算のために研ぎ澄まされるオープンなソフトウェアはありません。 存在するこれらの商用のものは数万ドルから数十万ドルの費用がかかり、普通の人々には利用できません。 もちろん、熱伝達を計算するためだけのオープンコードがありますが、実際の衛星を完全に当てにするには、かなり踊る必要があります。
普通の人には必要ないと言うでしょうが、これは衛星を作るためにあなた自身の小さな会社を作りたくない限りです。 ほとんどの国内の民間宇宙会社はそのようなソフトウェアのためのお金を持っていません、そして多くの外国企業は持っていません。
そして、あなたがコースや卒業プロジェクトで彼自身の衛星を設計する学生であるならば? 30日間の試用版では不十分な場合があります。
そして、放射熱伝達を理解したい場合は? または、他のアプリケーションにレイトレーシングメソッドの適切な実装を使用しますか?
つまり、スペースだけでなく、多くのアプリケーションがあります。
トリウム
THORIUMのアイデアは、2007年にベニスで開催されたIASS会議でShaenkoで生まれ、ボーイングのモスクワ支店にある787旅客機の迎撃機の強さを計算する自動化を反映して発展しました。

ラジオアストロン
当時、アレクサンダーは、レベデフ物理研究所のアストロ宇宙センターの大学院で勉強していました。 レベデフ。 そこで、当時、彼らは電波アストロン宇宙望遠鏡の製作を終え、ミリメトロンについて考えました。

ミリメトロン
Millimetronでは、約10メートルの大型ミラーを約4 K(-269 C)の温度に維持するのに数年かかりました。 これを行うために、太陽と地球の熱放射から繊細な機器を保護するポリマー金属化フィルムで作られた多層傘の影に鏡を置くことが計画されています。 傘は「熱シールド」と呼ばれていました。 アメリカのライバルJWSTである宇宙望遠鏡James Webbについてもまったく同じです。
熱シールドの実際の形状は、20メートルのフィルムパネルを少し間隔をあけてくしゃくしゃにしたものです。 これは、熱がどのように分配されるかを理解するために、多少なりとも大きな折り目をシミュレートする必要があることを意味します。 さらに、異なる層の温度は非常に異なります-太陽に照らされた層の約+100 Cから、ミラーに面する層の-223 Cまでです。 この散布により、材料の特性が大きく変わりました。
既存の和解コードでは、これらすべてを考慮に入れることができなかったため、THORIUM-熱光学放射反復型ユニバーサルモジュールが誕生しました。 これは、2007年末に発生した2つのアイデアに基づいています。
- 3次元グラフィックスの放射経路を計算するために、多くのソフトウェアとハードウェアが開発されました。外側の熱交換は空間で放射されるため、熱伝達の計算にグラフィックスからの動作時間を使用できます。
- モデル内に多数の要素がある複雑な構造を計算する場合、計算を開始する前に、どの要素がどの要素と放射を交換するかを覚えてはいけません。 長期にわたる統合のすべてのステップでこれを見る方がより有益です。
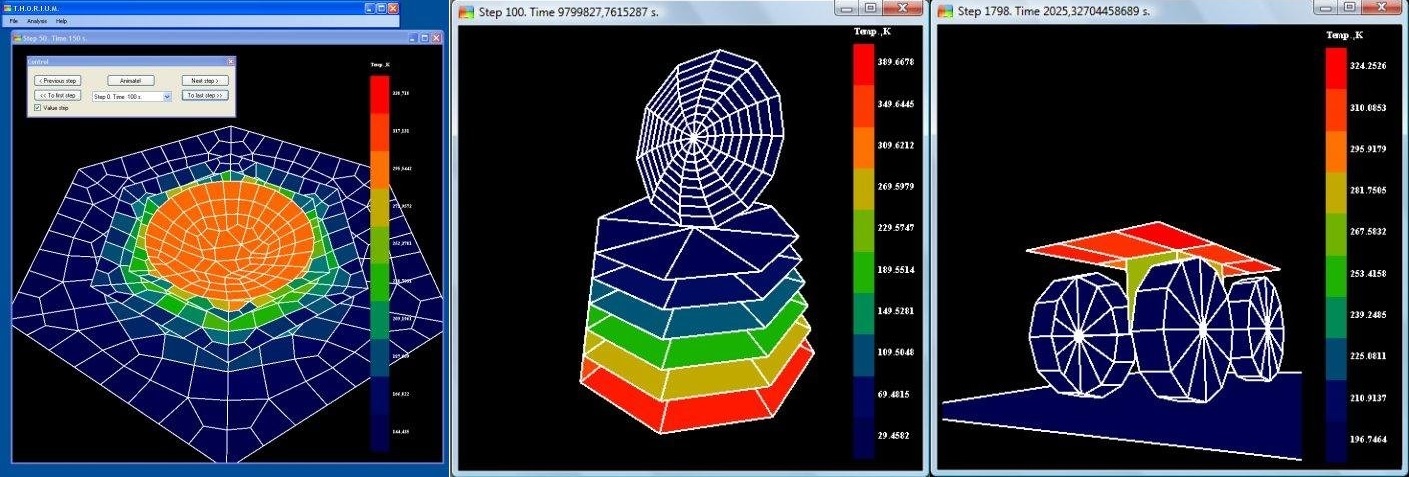
これらの2つの原則は、VB.NETの古いコードと新しいコードの両方に実装されました。 ミリメトロンは救われ、THORIUMは独自の生活を送り始め、小型デバイスの熱管理システム(COTS)の設計を支援しました。 たとえば、COTR DX1およびMKA-N、ダウリアの小型デバイスは、その助けを借りて設計されました。
ダウリエフスキーMKA-Nとの古いトリウムのビドス

トリウムのDX1
数学の観点から、THORIUMは、材料の熱物理特性と熱光学特性のばらつきを考慮して、非定常放射伝導熱伝達の微分方程式系を解きます。 これらの方程式は次のようになります。

どこで
c iはi番目の要素の比熱です。 ρiはその密度です。 V iは要素の体積です。 T iは要素の温度です。 tは時間です。 N i nは、i番目の要素と共通の面を持つ要素の数です。 Qn k iは、熱伝導率を介してi番目の要素のk番目の要素から送信される電力です。 S iはi番目の要素の面積です。 Qe iは、i番目の要素の放射放射束の密度です。 Qr ijは、放射を介してj番目の要素からi番目の要素に送信される電力です。 Nはモデル内の要素の数です。 Qr j mは、m番目の外部ソースから放出され、i番目の要素で吸収される放射のパワーです。 Mは放射線源の数です。 Qi i pはi番目の要素のp番目の内部熱源からの熱、Pは内部熱源の数です。
数Nは10 5を超える場合があり、要素のプロパティと境界条件は時々非常に急速に変化する可能性があります。たとえば、デバイスの電源を入れたり、太陽から影を出たりすると、10〜20ターンを統合する必要があり、これは約120,000秒です。
したがって、そのようなシステムを統合するための優れた方法を探すことは、著者、宇宙飛行士、および工学全体にとって非常に有用です。
誰が興味を持っている-コメントを書いたり、アレクサンダーにメール-ark4110@gmail.com。