Pythonには、ソフトウェアソリューションの実装の容易さ、明確で簡潔なコード、多数のライブラリの存在、活発なコミュニティなど、多くの魅力的な利点があります。 同時に、よく知られているpythonの遅さは、「重い」計算への適用を制限することがよくあります。 多くのタスクで、GPUでの並列コンピューティングにCUDAテクノロジーを使用することで、計算の大幅な高速化を実現できます。 この短い研究の目的は、GPUコンピューティングに効果的にpythonを使用する可能性を分析し、さまざまなpythonソリューションのパフォーマンスをC実装と比較することです。
はじめに
活動のタイプごとに、数値モデリングの問題に対処することがよくあります。 多くの場合、CUDAテクノロジーを使用して、GPUでの並列コンピューティングの機能を使用して計算を高速化しますが、プログラムはCで記述されています。同時に、便利で高速なため、Python柔軟で簡潔、
テストタスク
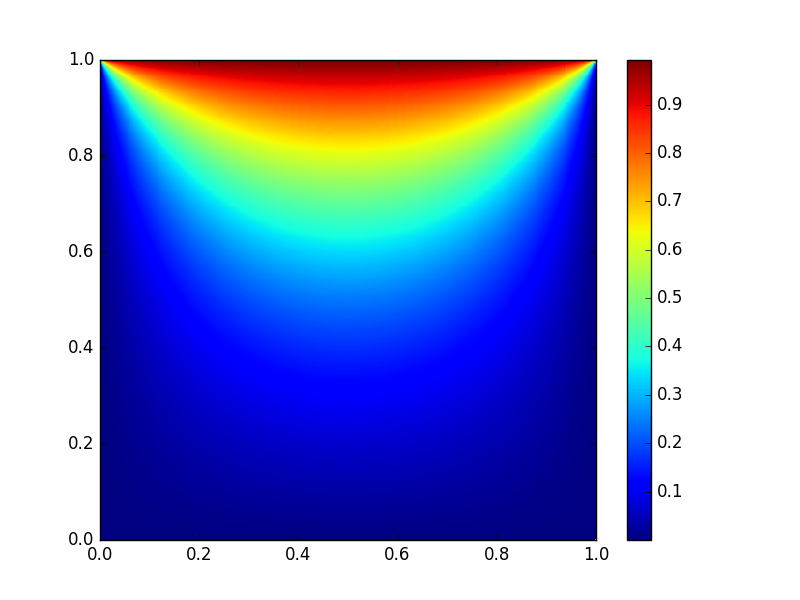
テストの問題とテスト条件の選択は、実際の問題の性質によって決定され、その解決のために、将来Pythonを使用することが計画されています。 この場合、最も単純な問題、つまり明示的な有限差分スキームを使用して2次元熱方程式を解く問題が選択されました。 この問題は、境界に温度値が与えられた正方形の領域で考慮されました。 xとyのグリッドノードの数は同じで、nに等しくなります。 記事の冒頭の図は、テスト問題に対する定常状態のソリューションを示しています。
アルゴリズムと試験条件
問題を解決するためのアルゴリズムは、次の擬似コードで表すことができます。
u0 u, u0 u for(i = 0; i < nstp/2; i++) u , u0 u0 , u (u0)
以下に示すすべてのテストで、各方向の正方形グリッドノードの数(n)は512から4096の範囲で、nstp = 5000でした。
ソフトウェアとハードウェア
テストはパーソナルコンピューターで実行されました。
Intel®Core(TM)2 Quad CPU Q9650 @ 3.00GHz、8 Gb RAM
GPU:Nvidia GTX 580
オペレーティングシステム:CUDA 7.5がインストールされたUbuntu 16.04 LTS
Cの実装
さらにすべてのpython実装を、このセクションで説明したCプログラムを使用して得られた結果と比較しました。
Cコード
#include <stdio.h> #include <time.h> #include <cuda_runtime.h> #define BLOCK_SIZE 16 int N = 512; //1024; //2048; double L = 1.0; double h = L/N; double h2 = h*h; double tau = 0.1*h2; double th2 = tau/h2; int nstp = 5000; __constant__ int dN; __constant__ double dth2; __global__ void NextStpGPU(double *u0, double *u) { int i = blockDim.x * blockIdx.x + threadIdx.x; int j = blockDim.y * blockIdx.y + threadIdx.y; double uim1, uip1, ujm1, ujp1, u00, d2x, d2y; if (i > 0) uim1 = u0[(i - 1) + dN*j]; else uim1 = 0.0; if (i < dN - 1) uip1 = u0[(i + 1) + dN*j]; else uip1 = 0.0; if (j > 0) ujm1 = u0[i + dN*(j - 1)]; else ujm1 = 0.0; if (j < dN - 1) ujp1 = u0[i + dN*(j + 1)]; else ujp1 = 1.0; u00 = u0[i + dN*j]; d2x = (uim1 - 2.0*u00 + uip1); d2y = (ujm1 - 2.0*u00 + ujp1); u[i + dN*j] = u00 + dth2*(d2x + d2y); } int main(void) { size_t size = N * N * sizeof(double); double pStart, pEnd, pD; int i; double *h_u0 = (double *)malloc(size); double *h_u1 = (double *)malloc(size); for (i = 0; i < N*N; ++i) { h_u0[i] = 0.0; h_u1[i] = 0.0; } pStart = (double) clock(); double *d_u0 = NULL; cudaMalloc((void **)&d_u0, size); double *d_u1 = NULL; cudaMalloc((void **)&d_u1, size); cudaMemcpy(d_u0, h_u0, size, cudaMemcpyHostToDevice); cudaMemcpy(d_u1, h_u1, size, cudaMemcpyHostToDevice); cudaMemcpyToSymbol(dN, &N, sizeof(int)); cudaMemcpyToSymbol(dth2, &th2, sizeof(double)); dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE, 1); dim3 dimGrid(N/BLOCK_SIZE, N/BLOCK_SIZE, 1); for(i = 0; i < int(nstp/2); i++) { NextStpGPU<<<dimGrid,dimBlock>>>(d_u0, d_u1); NextStpGPU<<<dimGrid,dimBlock>>>(d_u1, d_u0); } cudaMemcpy(h_u0, d_u0, size, cudaMemcpyDeviceToHost); cudaFree(d_u0); cudaFree(d_u1); pEnd = (double) clock(); pD = (pEnd-pStart)/CLOCKS_PER_SEC; printf("Calculation time on GPU = %f sec\n", pD); } free(h_u0); free(h_u1); return 0; }
計算では、N = 512の場合、GPUで並列化されたCプログラムの実行時間は0.27秒であり、CPUでのアルゴリズムの順次実装の場合は33.06秒です。 つまり、CPU / GPUの加速は約120倍です。 Nを増やしても、加速度は減少しません。
Numbaを使用したPython
Numbaライブラリには、Pythonコードをバイトコードにコンパイル(ジャストインタイム)する機能があり、パフォーマンスはCまたはFortranコードに匹敵します。 Numbaは、CPU上だけでなくGPU上でもPythonコードのコンパイルと実行をサポートしますが、Numbaライブラリを使用するプログラムのスタイルと外観は純粋にPythonのままです。
この場合、プログラムは次のようになります
from numba import cuda import numpy as np import matplotlib.pyplot as plt from time import time n = 512 blockdim = 16, 16 griddim = int(n/blockdim[0]), int(n/blockdim[1]) L = 1. h = L/n dt = 0.1*h**2 nstp = 5000 @cuda.jit("void(float64[:,:], float64[:,:])") def nextstp_gpu(u0, u): i,j = cuda.grid(2) if i > 0: uim1 = u0[i-1,j] else: uim1 = 0. if i < n-1: uip1 = u0[i+1,j] else: uip1 = 0. if j > 0: ujm1 = u0[i,j-1] else: ujm1 = 0. if j < n-1: ujp1 = u0[i,j+1] else: ujp1 = 1. d2x = (uim1 - 2.*u0[i,j] + uip1) d2y = (ujm1 - 2.*u0[i,j] + ujp1) u[i,j] = u0[i,j] + (dt/h**2)*(d2x + d2y) u0 = np.full((n,n), 0., dtype = np.float64) u = np.full((n,n), 0., dtype = np.float64) st = time() d_u0 = cuda.to_device(u0) d_u = cuda.to_device(u) for i in xrange(0, int(nstp/2)): nextstp_gpu[griddim,blockdim](d_u0, d_u) nextstp_gpu[griddim,blockdim](d_u, d_u0) cuda.synchronize() u0 = d_u0.copy_to_host() print 'time on GPU = ', time() - st
ここでいくつかの便利な機能に注意してください。 まず、この実装ははるかに短く、より視覚的です。 ここでは、コードをはるかに読みやすくする2次元配列を使用しました。 第二に、C実装で
cudaMemcpyToSymbol(dN, &N, sizeof(int));
などの関数を実行してすべての定数(Nなど)を渡す必要があった場合
cudaMemcpyToSymbol(dN, &N, sizeof(int));
ここでは、通常のpython関数のようにグローバル変数を使用しています。 最後に、実装にはC言語とGPUアーキテクチャの知識は必要ありません。
このコードは、後で示すように、サイズがn * nの1次元配列を使用する場合に簡単に書き換えることができます。これは、実行速度に大きく影響します。
ここにコードがあります
from numba import cuda import numpy as np import matplotlib.pyplot as plt from time import time n = 512 blockdim = 16, 16 griddim = int(n/blockdim[0]), int(n/blockdim[1]) L = 1. h = L/n dt = 0.1*h**2 nstp = 5000 @cuda.jit("void(float64[:], float64[:])") def nextstp_gpu(u0, u): i,j = cuda.grid(2) u00 = u0[i + n*j] if i > 0: uim1 = u0[i-1 + n*j] else: uim1 = 0. if i < n-1: uip1 = u0[i+1 + n*j] else: uip1 = 0. if j > 0: ujm1 = u0[i + n*(j-1)] else: ujm1 = 0. if j < n-1: ujp1 = u0[i + n*(j+1)] else: ujp1 = 1. d2x = (uim1 - 2.*u00 + uip1) d2y = (ujm1 - 2.*u00 + ujp1) u[i + n*j] = u00 + (dt/h/h)*(d2x + d2y) u0 = np.full(n*n, 0., dtype = np.float64) u = np.full(n*n, 0., dtype = np.float64) st = time() d_u0 = cuda.to_device(u0) d_u = cuda.to_device(u) for i in xrange(0, int(nstp/2)): nextstp_gpu[griddim,blockdim](d_u0, d_u) nextstp_gpu[griddim,blockdim](d_u, d_u0) cuda.synchronize() u0 = d_u0.copy_to_host() print 'time on GPU = ', time() - st
ピクダ
テスト済みのpythonライブラリの2番目はPyCUDAライブラリでした。 Numbaとは異なり、ここでは開発者から、Cでカーネルコードを記述する必要があります。そのため、この言語の知識がなくてはできません。 一方、コア自体は別として、Cで記述する必要はありません。
PyCUDAを使用するコードは次のとおりです
import pycuda.driver as cuda import pycuda.autoinit from pycuda.compiler import SourceModule import numpy as np import matplotlib.pyplot as plt from time import time n = 512 blockdim = 16, 16 griddim = int(n/blockdim[0]), int(n/blockdim[1]) L = 1. h = L/n dt = 0.1*h**2 nstp = 5000 mod = SourceModule(""" __global__ void NextStpGPU(int* dN, double* dth2, double *u0, double *u) { int i = blockDim.x * blockIdx.x + threadIdx.x; int j = blockDim.y * blockIdx.y + threadIdx.y; double uim1, uip1, ujm1, ujp1, u00, d2x, d2y; uim1 = exp(-10.0); if (i > 0) uim1 = u0[(i - 1) + dN[0]*j]; else uim1 = 0.0; if (i < dN[0] - 1) uip1 = u0[(i + 1) + dN[0]*j]; else uip1 = 0.0; if (j > 0) ujm1 = u0[i + dN[0]*(j - 1)]; else ujm1 = 0.0; if (j < dN[0] - 1) ujp1 = u0[i + dN[0]*(j + 1)]; else ujp1 = 1.0; u00 = u0[i + dN[0]*j]; d2x = (uim1 - 2.0*u00 + uip1); d2y = (ujm1 - 2.0*u00 + ujp1); u[i + dN[0]*j] = u00 + dth2[0]*(d2x + d2y); } """) u0 = np.full(n*n, 0., dtype = np.float64) u = np.full(n*n, 0., dtype = np.float64) nn = np.full(1, n, dtype = np.int64) th2 = np.full(1, dt/h/h, dtype = np.float64) st = time() u0_gpu = cuda.to_device(u0) u_gpu = cuda.to_device(u) n_gpu = cuda.to_device(nn) th2_gpu = cuda.to_device(th2) func = mod.get_function("NextStpGPU") for i in xrange(0, int(nstp/2)): func(n_gpu, th2_gpu, u0_gpu, u_gpu, block=(blockdim[0],blockdim[1],1),grid=(griddim[0],griddim[1],1)) func(n_gpu, th2_gpu, u_gpu, u0_gpu, block=(blockdim[0],blockdim[1],1),grid=(griddim[0],griddim[1],1)) u0 = cuda.from_device_like(u0_gpu, u0) print 'time on GPU = ', time() - st
Cコードのローカル挿入を除いて、すべて純粋なpythonのように見えます。
性能比較
図1および表1は、テストコードの実行時間(秒単位)のCコード実行時のグリッドサイズn(CUDA Cカーブ)と、Numbaライブラリおよび2次元配列(Numba 2DArr)を使用したPython実装(ライブラリを使用)の依存性を示していますNumbaおよび1次元配列(Numba 1DArr)、PyCUDAライブラリ(PyCUDA曲線)。

図1
| n | クーダC | ヌンバ2ダー | ヌンバ1ダー | ピクダ |
|---|---|---|---|---|
| 512 | 0.25 | 0.8 | 0.66 | 0.216 |
| 1024 | 0.77 | 3.26 | 1.03 | 0.808 |
| 2048 | 2.73 | 12.23 | 4.07 | 2.87 |
| 3073 | 6.1 | 27.3 | 9.12 | 6.6 |
| 4096 | 11.05 | 55.88 | 16.27 | 12.02 |
図2は、さまざまなpython実装のランタイムとCコードのランタイムの関係を示しています。 図からわかるように、最も遅いのは、2次元配列を使用したNumbaライブラリを使用した実装です。 同時に、このアプローチは最も明白でシンプルです。 興味深いことに、2次元配列を1次元配列に開発すると、コードが約3倍高速化されます。 最速の解決策は、PyCUDAライブラリを使用することでした。 同時に、上記のように、Cでカーネルを記述する必要があるため、このライブラリを使用するのは多少難しくなります。ただし、このようなpythonプログラムのコストは完全にCで記述されたプログラムよりも5〜8%低くなります。
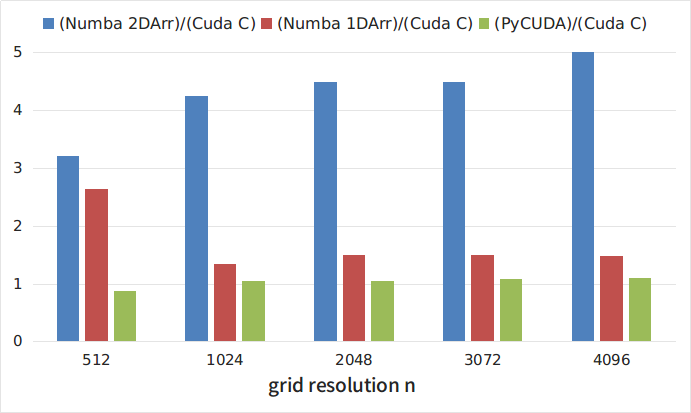
図2
結論
奇跡はなく、最も単純で明白な解決策が同時に最も遅くなることが判明しました。 同時に、既存のライブラリは、純粋なCコードの速度に匹敵するpythonプログラムの速度を達成できます。 開発者は、既存のライブラリを使用して、高レベルのソリューションを選択できます。 ただし、この選択は、開発速度とプログラム実行速度の妥協点です。
参照資料
» Numbaライブラリドキュメント
» ヌンバのケーススタディ
» PyCUDAライブラリドキュメント
» PyCUDAの使用例