問題の声明

これは2番目の最終記事です。 目標を思い出してください。DCモーターがあります。 タスクは、このエンジンに関連する現在の設定で制御ループを実装できるデバイスを開発、組み立て、テストすることです。 ストールしたエンジン（カウンターEMFなし）で必要な過渡時間は10ミリ秒以下です。



テキストは2つの記事に分かれています。

• 1.モーターの抵抗とインダクタンスの測定
• 2.制御回路の開発

コントロールアイロンのレイアウトは次のようになります。

望ましい結果

システム全体はブラックボックスのようなものです

だから、全体の考えは、エンジンに流れる電流の強さを直接設定したいということです。 コントローラーとエンジンを組み合わせる場合、次のようなものが欲しいです。









ここで、J（t）は電流リファレンス、I（t）はモーターを流れる電流です。 入力信号と出力信号が法則τI '（t）+ I（t）= J（t）に従って接続されるようにしたいと思います。 この法則は任意に選択され、私はこの微分方程式が好きです。 巧妙な言葉で、それは一次の非周期的リンクと呼ばれます。 この法律に従うコントローラーには、いくつかの回路に独自のシンボルがあります。







シングルリンク効果に対するこのようなリンクの反応は次のとおりです。









これは、さまざまな振動のない美しい指数関数的な収束です。このため、この形式が選択されました。 式τI '（t）+ I（t）= J（t）の定数tauは時定数と呼ばれます。これは、1回のジャンプに反応してプロセスが最終値の63％に達する時間です。 遷移プロセスの時間を最終値の98％に達する時間として定義する場合、これは約5タウです。 問題のステートメントでは、遷移プロセス時間は10ミリ秒を超えてはならないため、 τ= 0.002を取ります。

ブラックボックスを少し開きます

ブラックボックスを開くと、次のようになります。







ブラックボックスの入力で信号J（t）を出力し、出力で流れる電流I（t）を取得します。 ブラックボックス内には、2つのエレベータがあります。ターミナルUの電圧を接続する独自のディフューザを備えたエンジン（t）に流れる電流I（t）と、レギュレータ自体は、電流J（t）に応じて電圧U（t）を供給するそして実際に流れる電流I（t）。



コントローラーが入力誤差E（t）を取るとしましょう。これは、目的の電流と実際の電流の差であり、出力は電圧U（t）を与えます。 私たちのタスクは、E（t）とU（t）を接続する拡散を見つけることです。そうすれば、コントローラーarduinoのプログラミング方法が明確になります。



そのため、現在のタスクと実際の電流を、選択した法則に従って関連付ける必要があります。









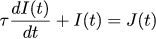
ラプラス変換を適用します（初期値はゼロ）：









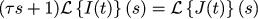
そして、次の割合を作ります：









念のため、制御理論では、この割合を伝達関数と呼びます。



エラーE（t）は、希望の電流強度と実際の電流強度の差として定義します。









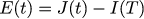
電流ループを調整するには、モーターシャフトを固定します。したがって、角速度はモーターディフューザーから離れます。









前の記事で、モーター端子の電圧と流れる電流の強さの関係を推定しました（ローターを固定した場合）：









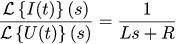
この比率を式（1）の比率に分割してみましょう。









ほぼ完了しましたが、ラプラス座標から通常の一時座標に移動するために残っています。 まず、比率を開きます。









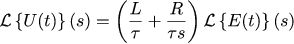
Laplace変換テーブルを装備すると 、次のことがわかります。









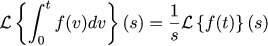
そして、これは、電圧U（t）とタスクE（t）の誤差を次の法則に従って接続する必要があることを意味します。









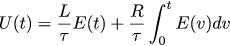
したがって、システム全体の動作を非周期的な1次ユニットとして選択すると、必要なコントローラーは通常のPIコントローラーにすぎないことがわかります。

実現

コントローラのコードはこちらにあります。 このプログラムは非常に標準的なものであり、注意すべき唯一の点は、atmegaには浮動小数点を扱うための正常性がないことです。 したがって、すべての作業は固定小数点と整数変数で行われます。

レギュレーターの動作確認

レギュレーターの動作を確認するために、入力で蛇行信号と正弦波信号を割り当てます。

蛇行

ここで 、実験データを取得できます。初期状態がゼロから、I0 = 4Aで必要な電流強度を設定し、実際に流れる電流を測定します。



次に、そのような条件下で流れる電流がどの法則で変化するかを紙の上で計算します。 この1対1は、前の記事で行ったことと一致しています。









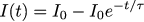
理論曲線が実際のデータに最も近く、先に選択した時定数と比較するように、パラメーターの値を選択してみましょう。 パラメータ選択コードはこちらにあります。



制御ループが蛇行半サイクルで動作する結果は次のとおりです。









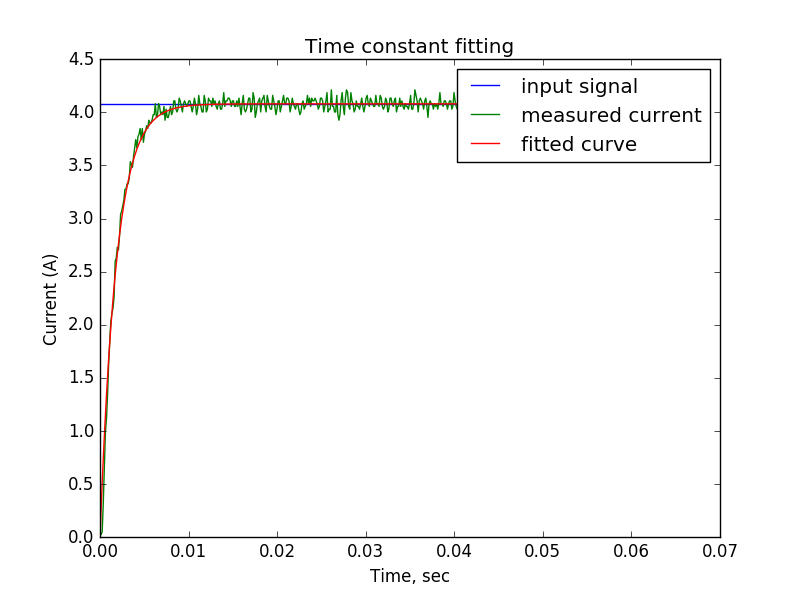
最小二乗法では、パラメーターの最適値は.00184であり、選択した時定数.002に非常に近いことがわかります。 移行プロセスは10ミリ秒以内であり、問​​題の定式化で彼に割り当てられたことが明確にわかります。

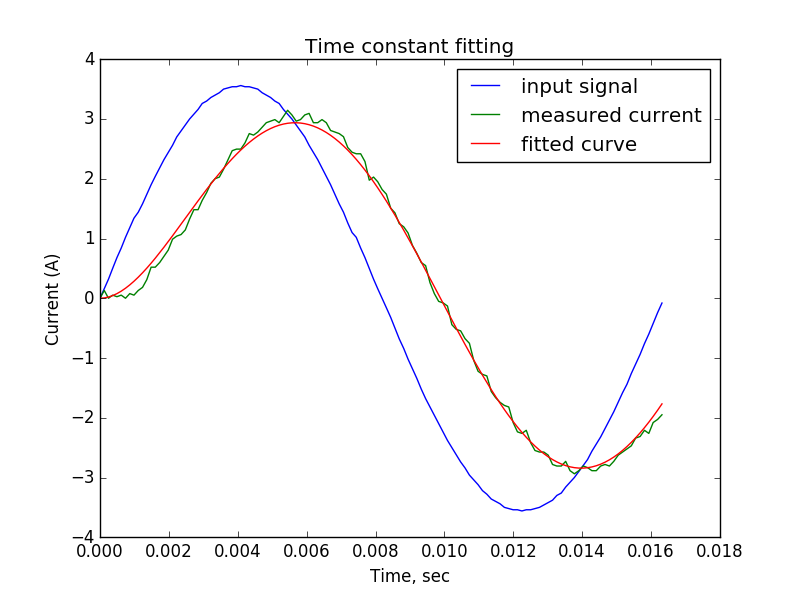
正弦波

念のために、2番目のチェックでも、計算はすべて前の記事から取られています。 正弦波基準では、電流強度I（t）は次の法則に従って変化するはずです。









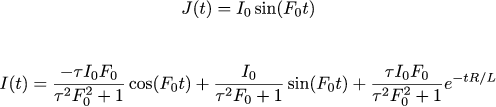
理論曲線のパラメータを選択するためのコードは、 ここで取得できます。 彼は時定数が.00196であり、計算された2msのパラメーターに近いことを教えてくれました。



これは、正弦波入力信号に作用する制御ループの結果です。

おわりに

一般的に、悪魔は彼が描かれているほどひどいものではありません。 科学のアラスタに感謝します！ 近い将来、（電圧を制御することによって）倒立振子を組み立てるのに少し時間を費やそうとしますが、アンペア数を直接制御することにより、振子自体のレギュレーターの計算が簡単になります。