この記事では、一般的な金融リスク評価ツールVaR （ ValueAtRisk ）を紹介します。 その際、最小限の経済用語、数学用語、統計用語を使用するようにします。
VaRの主なアイデアは、80年代にJPモーガンで開発され、適用されました。 VaRは、1993年に、デリバティブ（デリバティブ金融商品）を扱うための「ベストプラクティス」の一部としてGroup of Thirty（G-30）によって承認されたときに広く使用されました。 その後、 バーゼルIIシステム（銀行規制に関する一連の国際的な推奨事項）を使用した銀行のリスク指標の1つになりました。 VaRで使用されているアイデアは、1952年にノーベル経済学賞を受賞したガリアマルコヴィッツの初期の作品にまでさかのぼることができます。
なぜVaRが必要なのですか？
VaRには多くの用途があります。
- 銀行は、部門および銀行一般によって現在のリスクを決定します。
- トレーダーは、取引戦略でVaRを使用します（たとえば、いつ取引を終了するかを決定するため）。
- 個人投資家がリスクの少ない投資を選択する。
リスク管理
最初に、リスク管理とは何か、なぜこれが必要なのかを見てみましょう。
「リスク管理とは、投資決定の不確実性を検出、分析、作成、または軽減するプロセスです。 本質的に、リスク管理は、投資家またはファンドマネージャーが潜在的な損失を分析して評価し、投資目標とリスク許容度を考慮して必要な措置を講じる（または行わない）ときに常に発生します。
→ ソース
なぜリスク管理が重要なのですか？ ダニエルカーネマンは 、彼の著書「 Think Slowly ... Decide Quickly 」で、人々は勝つことよりも失うことを好まないと主張しています。 つまり、ある人が50％で110ドルを獲得し、50％で100ドルを失うように申し出られた場合、潜在的な利益は大きくなりますが、ほとんどの場合拒否します。 著者は、この損失を非対称と呼びます。
私たちは、人々が非常に敏感である可能性のある損失の予測に取り組みます。 しかし、VaRに進む前に、 リスク管理を想像することは不可能であるボラティリティの概念について話す必要があります。
ボラティリティについて少し
まず、2つの例を考えます。
例1-昨年、株Aを終日3％成長させるか、-1％失います。 さらに、これら2つのイベントは独立しており、同様に発生する可能性がありました。 投資額が100ドルであれば、明日はトレンドが続き、同じ確率で3ドルを受け取るか、-1ドルを失う可能性が高いと言えます。 つまり、+ 3 $を獲得する確率は50％であり、-1 $を失う確率も50％です。 毎日期待される利益は1ドル（3 $ * 50％-1 $ * 50％）であるとも言えます。 しかし、後で見るように、 期待される利益は、リスク管理に関心があるものではありません。 私たちにとって重要なのはまさに損失であり、可能性のある損失についてはここですべてが明らかです-50％の確率で1ドルのコストを失う可能性があります 。
ランダム収入+ 3％または-1％
次に、 例2を見てみましょう。 過去1年間の株Bの毎日の収益に関する情報があります。 収入特性：
- 4つの値-4％、-3％、+ 5％、+ 6％のいずれかを取りました。
- 4つのイベントのそれぞれの確率は同じです-25％。
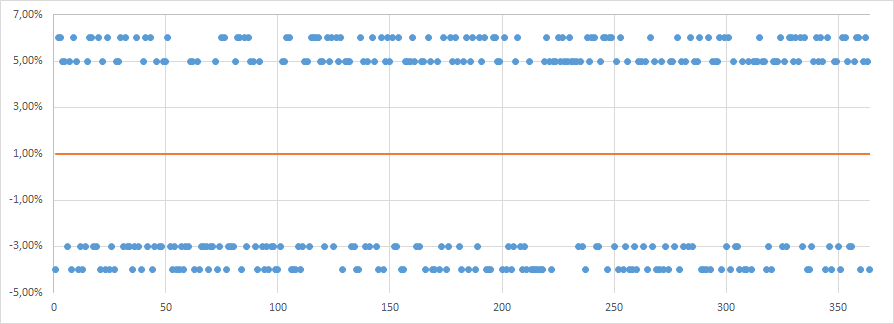
ランダム収入-3％、-4％、5％または6％
最初の例のように、平均値が+ 1％（-4％* 25％-3％* 25％+ 5％* 25％+ 6％* 25％）になるように特別に値を選択しました。 つまり、$ 100の株式がある場合、明日の期待値も$ 1になります。
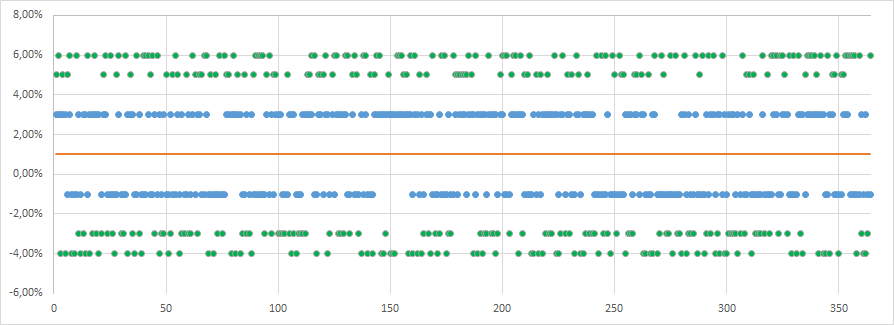
例1（-1％、+ 3％）と例2（-3％、-4％、5％、6％）の比較
2つのケースの期待値は同じ（+ 1％）ですが、2番目のケースでは損失の規模が大きくなる可能性があるため、リスクレベルは異なります。 これがボラティリティです。
ボラティリティ、ボラティリティ（英語のボラティリティ）-価格のボラティリティを特徴付ける統計的財務指標。 これは、金融リスク管理において最も重要な金融指標および概念であり、一定期間金融商品を使用するリスクの尺度です。
または、あなた自身の言葉では、ボラティリティは価値を広げる力です。 スプレッドが大きいほど、ボラティリティは高くなり、将来の価格についての仮定を立てることが難しくなります。 結論は、ボラティリティが高いほどリスクが高いことを示唆しています 。 ボラティリティは私たちが必要とする指標であると思われます。
しかし、ボラティリティには、リスク管理にとって重大な欠点が1つあります。 利益の広がりと損失の広がりの両方を考慮します。 たとえば、株価が急激に上昇すると、ボラティリティが増加します。 リスクは、可能性のある損失の観点から、同じレベルにとどまります。 この問題はVaRによって解決されますが、VaRに進む前に、損失の推定の問題に対処しましょう。
問題1 。 潜在的な損失を説明する方法は？
最初の例で明日の損失の予測が50％の確率で-1％である場合、2番目の例では状況はより複雑です。 私たちはそれを言うことができます：
- 25％の確率で、3％を失います。
- 25％の確率で、4％を失います。
- 50％の確率で、3％以上を失います。
これらの記述はすべて真実ですが、 可能な結果は4つしかありません 。 実際には、結果の数ははるかに多くなる可能性があります。 したがって、リスクの可能性について私たちができる声明の数は増えます。 そして、これは情報の報告と分析を複雑にします。
問題2.極端な値。
昨年、株価は-5％から5％の値を取りましたが、ある日、損失は-10％だったと想像してください。 1年の日数を364にすると（簡単にするために、週末と祝日は忘れてください）、-10％で繰り返される損失の確率は1/364 = 0.274％です。 0.274％の確率はかなり小さく、想像するのが難しく、だれかが一般的に考慮に値しないと感じるかもしれません。 この場合の対処方法
どちらの場合も、VaRは私たちの助けになります。
ヴァール
VaRを使用すると、一定の確率で損失を評価できます。 また、これは非常に簡単に行うことができるため、人はリスクの大きさを比較的簡単に想像できます。 VaRは次の質問に答えます。
「 特定のレベルの確率（自信）で一定期間に期待できる最大の損失とは」
たとえば、99％のしきい値を持つ100ドルのVaRは、次のことを意味します。
- 1％の確率で、日中に100ドル以上を失う可能性があります。
- 99％の確率で、日中に100ドル以上を失うことはありません。
これらのステートメントは両方とも同等です。
VaRは3つのコンポーネントで構成されます。
- 予測レベル/しきい値（通常95％または99％）;
- 予測時間間隔（日、月、または年）;
- 可能性のある損失（金額（通常はドル）またはパーセント）;
しきい値（この例では99％）を選択する機能は、多くの投資家にとって非常に便利な特性です。 この特性により、多くの投資家が「 最悪の場合、1日（月）にどれだけ失うことができるか 」 という疑問に対する答えに近づくことができます。 」
VaRを生成するには、 歴史的 、 共分散、およびモンテカルロ法の 3つの方法があります。
この記事では、統計の分野で最低限の知識を必要とし、私の意見では3つの中で最も直感的な方法であるため、 歴史的方法を検討します。
VaRカウント手順：
- 特定の期間（月、年）の収入の履歴データを収集します。
- データを昇順で並べ替えます。
- 予測を行うしきい値を選択し、しきい値を知っている最悪の値を「カットオフ」します。
わかりやすくするために、実際の例でこのVaRを見つけるプロセスを見ていきましょう。 例として、2015年のAppleの株価を見てみましょう。
手順：
1. 株式返品に関するデータをパーセンテージで取得します 。 たとえば、yahoo.finance.comからデータをダウンロードできます。 Yahooは、開始、終了などを提供します。 終値を検討します（閉じる*）。 yahooでは、日付は降順で並べ替えられるため、昇順で並べ替えることができます。 前日からの終値をパーセンテージで利益に変換します。 たとえば、価格が昨日10ドルで、今日が15ドルだった場合、利益率は（$ 15 -10 $）/ $ 10 = 50％になります。
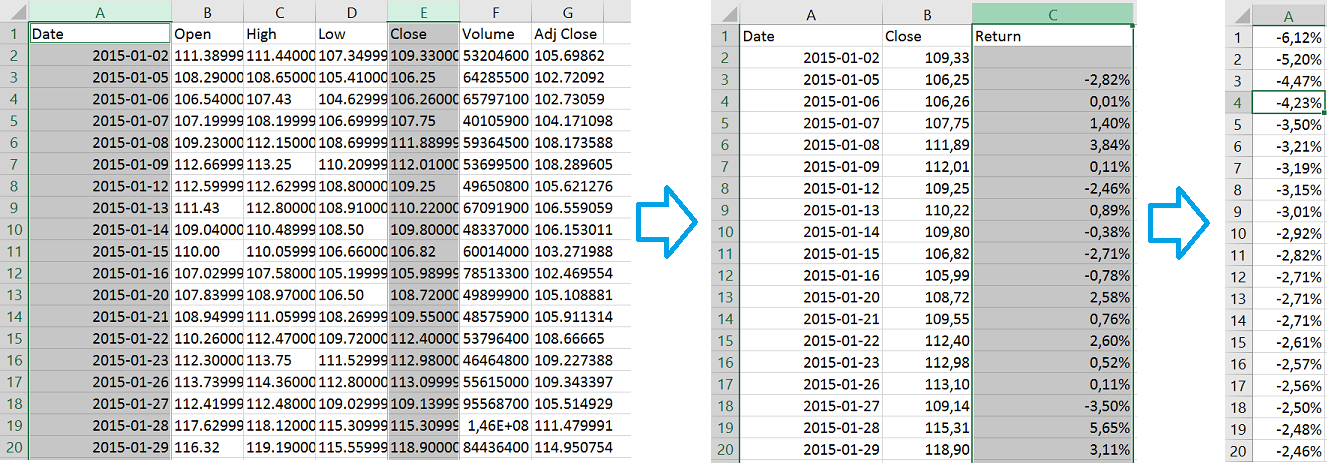Yahooからのデータを変換して並べ替える
2. 利益を昇順で並べ替えます （わかりやすくするために、ヒストグラムを作成しました）。
3.予測に使用するしきい値を選択し、しきい値を知っている最悪の値を「カットオフ」します 。 252営業日があります。 ケースの95％をカバーする評価を行いたい場合、 最悪の 5％を破棄します。この確率は低いと見なされます。 252日間の5％は13日間です（約12.6〜13）。 グラフを見ると、13番目の「最悪の日」の収入が-2.71％だったことがわかります。 95％の確率で2.71％を超える損失はないと言えるでしょう。 投資額が100ドルであれば、95％の確率で2.71ドルを超える損失はありません。 これは 、 2.71ドル以上を失うことができないという意味ではなく 、95％の確率について話している。 これで十分でない場合は、しきい値をたとえば99％に増やすことができます。
*調整ではなく終値を選択します。 調整してから クローズは一貫性がなく、時間とともに変化する可能性があります。 たとえば、株式分割が発生した場合。 私たちの目標は、この例を後で完成させる人々と数字が一致することです。
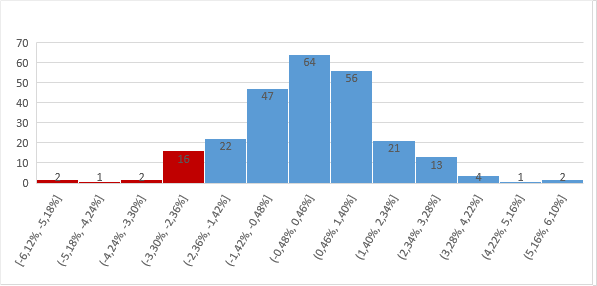Appleのデータを使用して例を終了し、別の興味深いグラフを示します。 チャートでは、水平方向の利益の範囲と垂直方向-利益が対応する間隔で減少した日数を確認できます。 このグラフは正規分布に非常に似ています 。 この事実は、VaRを計算する他の2つの方法を検討する次の記事で役立ちます。
コード例
public Double calculateHistoricalVar(List<Double> prices, Double confidenceLevel, Double amount) { if (prices.isEmpty()) { return 0d; } List<Double> returns = getReturns(prices); Collections.sort(returns); double threshold = (returns.size() * (1 - confidenceLevel)); int intPart = (int) threshold; Double decimalPart = threshold - intPart; Double rawVar = returns.get(intPart); Double interpolatedPart = decimalPart * (returns.get(intPart) - (returns.get(intPart + 1))); return rawVar + interpolatedPart; } private List<Double> getReturns(List<Double> prices) { List<Double> result = new ArrayList<>(prices.size()); for (int i = 1; i < prices.size(); i++) { result.add(prices.get(i) / (prices.get(i - 1)) - 1); } return result; }
一般的な歴史的手法とVaRの欠点について少し：
- 履歴データを使用して未来を予測します。 これは脆弱な仮定かもしれません。 過去の出来事が繰り返されると仮定しているため。 VaR（年、月、日）を計算するために、異なる時間間隔を使用してこれに対処することができます。 これについては以下で説明します。
- VaRは、しきい値以外の値、たとえば95％については何も言いません。 95％のしきい値でのVaRが$ 50で、観測数が100の2つの異なる株AとBを持つことができます。 AとBの95個の最適な観測値が同じで、-50 $〜45 $が1 $ずつ増加するようにします。 しかし、5つの最悪の利益は、A = {-1000 $、-800 $、-700 $、-600 $、-500 $}、およびB = {-100 $、-99 $、-98 $、-97 $、-96です。 $}。 明らかに、Bのリスクは高くなります。 しきい値（最大99％、99.9％、99.99％など）を増やすことで、これに対処することができます。 また、これらの欠点に対処するために特別に設計された方法もあります。たとえば、損失がVaRを超えた場合に損失を推定する条件付きVARです。 しかし、この記事ではそれらを考慮しません。
VaRを使用する際に生じる可能性のある質問：
- 期間の選択方法は？
- これに対する明確な答えはありません。それはすべて投資期間に依存します。 銀行は通常、VaRを数日間検討しますが、年金基金は、多くの場合、数ヶ月間VaRを検討します。
- 95％が整数のアイテム番号でない場合はどうなりますか？
- この例では、252日と95％のしきい値を使用しました。 切り取る要素は252 * 0.05 = 12.6です。 この例では、単純に丸めて13番目の要素を取りましたが、正確には、値はその中間にあるはずです。 残念ながら、この例では、12番目と13番目の要素は-2.71％です。 したがって、12番目の要素が-4％、13番目の要素が-3％であると想像してください。 その場合、VaRは-4％から-3％の間で、-3％に近くなります。 より正確には-3.6％。 ここで補間が役立ちます。 式は次のとおりです。
b +（ab）* k、ここでaは下限値、bは上限値、kは小数部（この場合は0.6）
-3％+（-4％+ 3％）* 0.6 = -3.6％
おわりに
VaRアプローチの利点は、複数の株式のセットまたは異なる証券の組み合わせに対して最適に機能することです。 たとえば、一連の債券と通貨のVaRは、それほど労力をかけずに見積もりを提供します。 また、考えられるシナリオの分析など、他の方法の使用は、証券間の相関関係（接続）のために非常に複雑です。
→ ソース