 あなたの多くはおそらく数独のようなパズルに精通しているでしょう。 おそらく、彼らは自動ソリューションのためのプログラムを実装しました。 数独のトピックはすでにハブで何度も議論されており、実践が示すように、答えを自動的に見つけるほとんどすべての方法は最終的には方向性検索に帰着します。 手動のソリューションでさえ同じ原則に準拠しているため、これは非常に自然なことです。 しかし、そうしないとどうなりますか?
あなたの多くはおそらく数独のようなパズルに精通しているでしょう。 おそらく、彼らは自動ソリューションのためのプログラムを実装しました。 数独のトピックはすでにハブで何度も議論されており、実践が示すように、答えを自動的に見つけるほとんどすべての方法は最終的には方向性検索に帰着します。 手動のソリューションでさえ同じ原則に準拠しているため、これは非常に自然なことです。 しかし、そうしないとどうなりますか?
この記事では、厳密に数学的なアプローチに基づいて、2012年に提案された非常に面白い方法を検討します。 ソフトウェア実装が添付されています。
ステージ0。問題の説明
まず、パズルの説明を覚えておいてください。 数独レイアウトのタスクは、1つの行、列、または強調表示された3x3ブロックに同じ番号が含まれないように、9x9フィールドに1から9までの数字を入力することです(図では太字の枠でブロックがマークされます)。 そのような詰め物の一意性も通常暗示されます;この事実は、高度な複雑さの問題の解決に役立ちます。 私たち(およびブルートフォースアルゴリズム)は、ソリューションの一意性の仮定を必要としません。 注意する必要があります:説明した方法を使用すると、最初に遭遇する解決策を見つけることができます。 この方法を使用したすべてのソリューションの列挙は不可能です(まあ、少なくとも非実用的です)。
ステージ1.タスクの形式化
正しく入力されたフィールドが何であるかを数学的に説明しましょう。 9x9のグリッドがあり、各セルには1から9までの1つの数字しかありません。81個の整数変数を導入するのが合理的ですが、代わりにブール値で操作します。 これにより、正式な論理的アプローチが可能になります。
多く紹介します 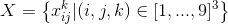 論理変数。次の意味を付与します。
論理変数。次の意味を付与します。 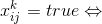 cageの中
cageの中 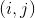 番号が書かれています
番号が書かれています 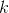 。 数独で正しいフィールドを決定すると、変数セットに導入するいくつかの制限が決まります。
。 数独で正しいフィールドを決定すると、変数セットに導入するいくつかの制限が決まります。
簡単にするために、まずq-local述語を導入します 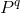 、そのパラメーターの1つがtrueである場合にのみtrue。 彼の正式な説明は次のとおりです。
、そのパラメーターの1つがtrueである場合にのみtrue。 彼の正式な説明は次のとおりです。
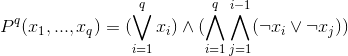
それを使用して、前述の4種類の制限を記述します。
- 各セルには、9つの数字のうち1つのみを含めることができます。
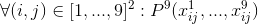
- 各行で、各数値は1回だけ発生します。
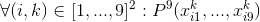
- 各列で、各番号は1回だけ発生します。
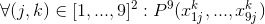
- 説明のための最も不快なケース-9つの3x3ブロックのそれぞれに正確に1回ずつ各番号が含まれています:
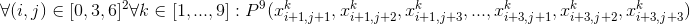
上記のすべての式を組み合わせて、量指定子を取り除くと、次のようになります。
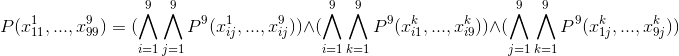
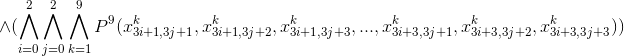
この式には、接続詞の標準形があります(述語 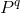 CNFにも記録されます)。これは、ソフトウェア処理に非常に便利な方法です。
CNFにも記録されます)。これは、ソフトウェア処理に非常に便利な方法です。
数独のすべての可能なフィールドを記述する一般的な公式を手にしています。 実際には、数独フィールドにはいくつかの手がかりがあります。 ケージ内の場合 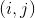 たくさんの価値がある
たくさんの価値がある 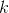 、それから私たちはそれを知っています
、それから私たちはそれを知っています 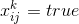 。 これに加えて、これらの条件下ではfalseでなければならない多くの変数を簡単に決定できます。 これらすべての数量を置き換えて、各条項を簡素化します。 さらに、式から重複する句を削除し(出現した場合)、結果の関数(まだCNFで)が完全にアライメントと方程式の各ソリューションを決定することを宣言する権利があります
。 これに加えて、これらの条件下ではfalseでなければならない多くの変数を簡単に決定できます。 これらすべての数量を置き換えて、各条項を簡素化します。 さらに、式から重複する句を削除し(出現した場合)、結果の関数(まだCNFで)が完全にアライメントと方程式の各ソリューションを決定することを宣言する権利があります 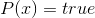 元の問題に対する独自のソリューションを提供します。 だから、概して、数独を数学的論理からの古典的な実現可能性問題に限定した。 NP完全であり、元のパズルの複雑さをある程度説明しています。
元の問題に対する独自のソリューションを提供します。 だから、概して、数独を数学的論理からの古典的な実現可能性問題に限定した。 NP完全であり、元のパズルの複雑さをある程度説明しています。
数式が特定の引数セットで真になるかどうかを調べることを目的としているため、数独を実行可能性の問題に限定したと言うのは完全に真実ではありません。 数独では、式が実行可能であることを事前に知っています。
単純な事実は、多くの場合、式が真になる引数の検索が実行可能性タスクとして理解されることです。
ステージ2.少しの数学的分析
この瞬間から、数独を解決することを忘れることができます。これは、説明した方法があらゆる実行可能性の問題に適しているためです。 そして、それを記述するためにいくつかの新しい表記法が必要です。
N個の論理変数で構成される式があるとします 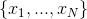 およびM句。 マトリックスを紹介します
およびM句。 マトリックスを紹介します 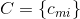 次のようなMxNサイズ
次のようなMxNサイズ
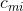 = mth句に次が含まれる場合
= mth句に次が含まれる場合 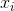 ;
; 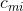 = -1、m番目の節に否定が含まれる場合
= -1、m番目の節に否定が含まれる場合 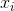 ;
; 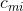 = mth句に含まれない場合は0
= mth句に含まれない場合は0 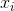 。
。
次に、ベクトルを紹介します 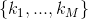 そのような
そのような 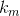 = {番号がmの句の変数の数}。
= {番号がmの句の変数の数}。
そして、最後に、みんなに 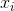 実数と一致する
実数と一致する 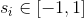 。
。 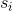 これは連続量であり、
これは連続量であり、 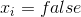 -1と等しい
-1と等しい 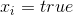 1に等しい
1に等しい 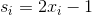 。
。
これで、これらすべてが必要な理由を理解できます。 各M句に関数を関連付けます 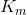 次のように定義されます。
次のように定義されます。
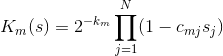
これらの関数は、0に変わるため良いです(因子の1つがゼロの場合) 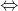 対応する意味を持つ対応する句
対応する意味を持つ対応する句 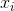 本当です。 さらに、因子を追加する
本当です。 さらに、因子を追加する 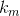 各関数がセグメントから値を取得することを保証します
各関数がセグメントから値を取得することを保証します 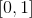 その定義の分野で。 しかし、それらの平方の合計はより興味深いものになります。
その定義の分野で。 しかし、それらの平方の合計はより興味深いものになります。
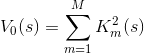
この合計は、上の元の方程式の解に対応するベクトルsでのみ消失するという点で注目に値します 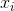 。 そして、これらのゼロはすべて、関数の局所的な最小値です(値の範囲のため)。
。 そして、これらのゼロはすべて、関数の局所的な最小値です(値の範囲のため)。
ステージ3.微分方程式系
方程式は、レコードの見かけの単純さにもかかわらず、実際には非常に不快です。 これは、非常に多数の引数を持つ大きな多項式です。 分析的に彼の最小値を見つけようとする必要さえありません。
いくつか追加してみましょう。
- 想像する
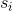 機能として
機能として 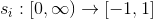 ;
; - 多くの機能を導入する
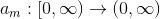 ;
; - 私たちの代わりに
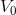 考えます
考えます 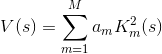
みんなから 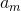 厳密に正の場合、方程式は最も重要な特性を失いません。
厳密に正の場合、方程式は最も重要な特性を失いません。
同時に 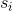 そして
そして 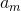 次の条件から見つけます。
次の条件から見つけます。
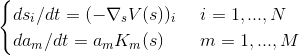
このエントリのは勾配演算子です。
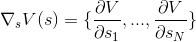
最初の方程式は、極値を見つけるための共役勾配法を明確に示唆しています。
2番目のものは少し複雑なので、著者に任せます。 要するに、システムがソリューションにより速く収束するために必要です。 私自身、これが本当かどうかは確認していません。
上の方程式 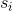 Vを区別することにより、明示的に書き換えることができます。
Vを区別することにより、明示的に書き換えることができます。

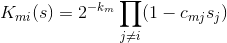
ポイント0の初期条件は任意です。 最後に、次の式を使用してソリューションを取得します。 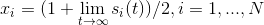
一般的に言えば、初期条件の意性に関する声明は誤りです。 このメソッドの著者は、ゼロメジャーの初期条件のセットでは答えが見つからないと主張しています。 ただし、セットは「小さい」ため、実際には無視できます。
ステージ4.最後に数値解
常微分方程式系を解く最も簡単で便利な方法の1つは、ルンゲクッタ法です。 Cash-Karpの名前を持つメソッドのバリアントを使用します。 次に、それについて簡単に説明します。
だから、方程式があります 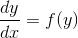 。 方程式では導関数の値を使用するため、パラメーターリストのxは省略します。
。 方程式では導関数の値を使用するため、パラメーターリストのxは省略します。 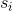 そして
そして 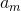 tに明示的に依存しないでください。 私たちにとっては簡単です。
tに明示的に依存しないでください。 私たちにとっては簡単です。
初期条件  、しかし値を見つける必要があります
、しかし値を見つける必要があります 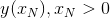 。
。
答えを見つけるために、シーケンスを作成します 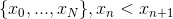 そして、値を計算します
そして、値を計算します 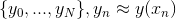 。
。
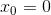 そして
そして 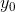 私たちはそれらを誘導の基礎と考えています。 さらに、ステップn <Nで、
私たちはそれらを誘導の基礎と考えています。 さらに、ステップn <Nで、 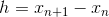 。 検索します
。 検索します 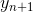 次の式に基づいて:
次の式に基づいて:
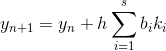 シーケンス
シーケンス 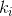 次の場所にあります:
次の場所にあります:
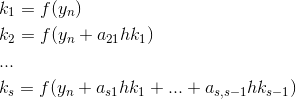
数字  、
、 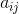 そして
そして 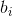 固定定数であり、その精度はメソッドの精度に大きく依存します(標準的な方法には定数もあります
固定定数であり、その精度はメソッドの精度に大きく依存します(標準的な方法には定数もあります 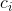 しかし、私たちの場合、それらは単に必要ではありません)。
しかし、私たちの場合、それらは単に必要ではありません)。
これらの係数のセットをまとめて「ブッチャーテーブル」と呼びます。

Cash-Karpメソッドの場合、次のようなテーブルがあります。
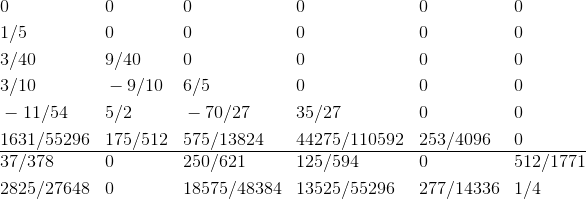
ここに2つのベクトルbがあります。 最初のものを使用する場合、各ステップで計算エラーは次のように評価されます。  。 そして、2番目のベクトルbを使用すると、誤差の推定値は
。 そして、2番目のベクトルbを使用すると、誤差の推定値は 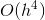 。 精度の低い値を数える
。 精度の低い値を数える 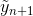 、ステップで絶対誤差を発見的に評価できます。
、ステップで絶対誤差を発見的に評価できます。 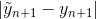 (4次と5次の決定の違い)。 そして、エラーが私たちに合わない場合、現在のステップhを別の値に置き換えて、現在の反復を再カウントできます。 特に、2つのオプションが可能です。
(4次と5次の決定の違い)。 そして、エラーが私たちに合わない場合、現在のステップhを別の値に置き換えて、現在の反復を再カウントできます。 特に、2つのオプションが可能です。
- 大きすぎる間違い-ステップを減らし、最初から反復を開始します。
- 小さすぎるエラー-ステップを増やし、次の反復を開始します(これにより、合計計算時間が短縮されます)。
すべてが計算されたら、検索プロセスを停止できます 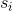 モジュロは、ユニティとはほとんど異なりません(0.1の差で十分です)。
モジュロは、ユニティとはほとんど異なりません(0.1の差で十分です)。
おわりに
確かに、このような単純なタスクには少々面倒です。 個人的には、このようなすべての資料を好奇心だけで理解しようとしました。そのような予期せぬ場所で数学が広く使われることはめったにないからです。
上記のすべてが実際に機能しますか? 著者はコードを共有しなかったので、私は自分で書かなければなりませんでした。
彼は問題を解決しますが、「世界で最も難しい」クラスの数独では、動作が非常に遅く、解決の期間は初期データ(つまり、ランダム性)に大きく依存します。 これがメソッドの問題なのか実装の問題なのか、確実に答えることはできません。 明らかなバグはありませんでした。
このトピックに本当に興味がある場合は、オリジナルを読むことを強くお勧めします。 メソッドの作成者が検討したすべての資料を網羅したわけではありません。 最後まで読んでくれてありがとう!
参照: