スクリーンスペースアンビエントオクルージョン

次に、DirectX11 APIを使用して、C ++プログラミング言語でスクリーンスペースアンビエントオクルージョンの拡散照明計算方法を実装する方法について説明します。



たとえば、平行光源を使用する場合、画面上のピクセルの色を計算する式を検討してください。

LitColor =アンビエント+拡散+鏡面反射

または、より正式には、拡散照明、吸収照明、鏡面照明の合計。 それらはそれぞれ次のように計算されます。

（素材の色）*（ソースの色）*（強度係数）

インタラクティブグラフィックスアプリケーションでは長い間、環境強度係数は一定でしたが、今ではリアルタイムで計算できます。 そのような方法の1つ-アンビエントオクルージョン、またはむしろその最適化-スクリーンスペースアンビエントオクルージョンについてお話したいと思います。 最初にアンビエントオクルージョンメソッドについて説明しましょう。 その本質は次のとおりです-シーンの各頂点が、シーンの残りの部分の「可視性」の度合いを決定する特定の要因を形成します。









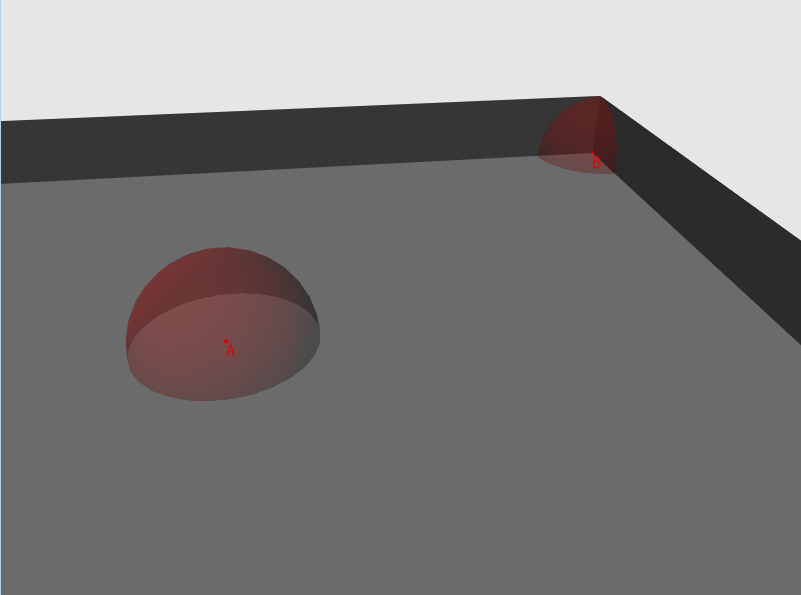
図1-部屋と2つのポイントを含む図面、各ポイントの「可視性」は球として描かれています



したがって、ランダムな方向の各頂点について、光線を離し、シーンのジオメトリとの交差点を見つけます。 次に、結果のラインの長さを計算し（交差が見つからなかった場合、指定されたシーンでビームに特定の最大長があると仮定します）、それをしきい値と比較します。 長さがしきい値を超える場合、ビームは「可視性」のテストに合格します。合格したテストの数を発射された光線の数で割ったものが「可視性」の要因になります。



明らかに、アルゴリズムの計算の複雑性が高いため、リアルタイムまたはオブジェクトのダイナミクスが高いシーンには適用できません。 また、この方法の有効性は、シーンの多角形の複雑さに大きく依存します。 事前に「可視性」を計算し、頂点データの一部として、またはテクスチャに保存できる場合は、このアプローチを適用するのが妥当です。



幸いなことに、CryTeckの担当者（少なくとも私が彼らが最初だと聞いた）は、リアルタイムで係数を計算する方法を思いつきました。 これは、スクリーンスペースアンビエントオクルージョンと呼ばれます。



私の実装のアルゴリズムは次のとおりです。

• 1. NDC（正規化されたデバイス座標）またはピクセルのテクスチャ座標を取得し、深度データを使用してカメラ空間のポイントに変換します。
  
  
  
  
• 2.このポイントからランダムな方向に、N本の光線を開始します。
  
  
  
  
• 3. N個の光線のそれぞれについて：
  
  
  
  
  • 3-a。 レイ（ベクトル）に特定の数（スカラー）を乗算（スケーリング）し、アイテム1のポイントに追加します。
  • 3-b。 結果のポイントをNDC空間に変換し、次にテクスチャ座標に変換します。
  • 3-c。 テクスチャから、このポイントの深度値を取得します。
  • 3番目。 取得した値が項目3-aで取得したポイントの深さよりも小さい場合、「オーバーラップ」があります（図2を参照）。 これらの値が同じ座標系に属していることを考慮に入れる必要があります。
  • 3-f。 「アイテム3aからのポイントがアイテム1からのポイントから遠いほど、このポイントからのオーバーラップの可能性は低くなります」という依存関係に基づいて、「オーバーラップ」係数を取得します。 その価値を蓄積します。
  
  
  
• 4. 「オーバーラップ」という共通の係数を取得します。これは、総オーバーラップ合計/ N光線に等しくなります。 共通因子は[0,1]に属し、可視性はオーバーラップに反比例するため、1-オーバーラップに等しくなります。

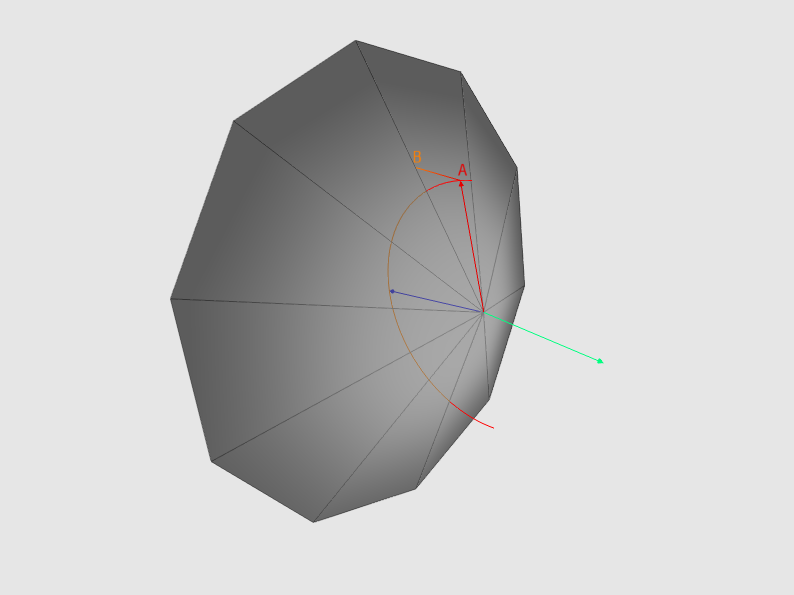
図2-法線ベクトルは青で表示され、アイテム3-aで取得されたベクトルは赤で表示されます。 薄緑色のベクトルはZ軸の方向であり、ポイントAの深さがポイントBの深さよりも大きい場合、これはオーバーラップです。 わかりやすくするために、図では正射影を使用しています（したがって、線ABは直線です）



ピクセルシェーダーでこのアルゴリズムを使用すると、レンダリング結果をテクスチャに書き込むと、可視性データを取得できます。 このテクスチャからのデータは、シーンの照明の計算にさらに使用できます。



それでは始めましょう。

1.コンバージョン

3次元座標から画面座標を取得するには、一連のマトリックス変換を行う必要があります。



一般的には、次の3つの変換があります。

• 1.ローカル座標からワールド座標へ-すべてのオブジェクトを共通の座標系に転送します
• 2.ワールド座標からビュー座標まで-「カメラ」を基準にしてすべてのオブジェクトを方向付けます
• 3.ビュー座標から投影座標まで-オブジェクトの頂点を平面に投影します。 透視投影法を使用します。これは、いわゆる同次除法-コンポーネントxの分割と、深さによる頂点-コンポーネントzを意味します。

パラグラフ1と2は重要ではないため、パラグラフ3に進みます。 射影行列を見てみましょう：









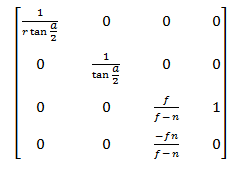
この行列を乗算した後、カメラ空間からの座標は投影空間に入ります









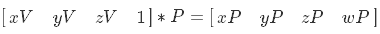
同種の分割が続きます。その結果、NDCスペースに移動します









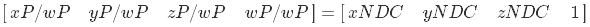
次に、逆変換を実装する方法を見てみましょう。 明らかに、最初にシェーダーのピクセル座標が必要です。 テクスチャ座標が（0,0）から（1,1）のNDC空間の画面領域全体をカバーする正方形を使用すると最も便利です。 頂点データは次のとおりです。

struct ScreenQuadVertex { D3DXVECTOR3 pos = {0.0f, 0.0f, 0.0f}; D3DXVECTOR2 tc = {0.0f, 0.0f}; ScreenQuadVertex(){} ScreenQuadVertex(const D3DXVECTOR3 &Pos, const D3DXVECTOR2 &Tc) : pos(Pos), tc(Tc){} }; std::vector<ScreenQuadVertex> vertices = { {{-1.0f, -1.0f, 0.0f}, {0.0f, 1.0f}}, {{-1.0f, 1.0f, 0.0f}, {0.0f, 0.0f}}, {{ 1.0f, 1.0f, 0.0f}, {1.0f, 0.0f}}, {{ 1.0f, -1.0f, 0.0f}, {1.0f, 1.0f}}, };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、D3D11_FILTER_MIN_MAG_MIP_POINTなど、テクスチャデータのポイント補間を設定する必要があります。 この正方形を描画することで、次の方法で頂点データをピクセルシェーダーに「転送」できます。

 VOut output; output.posN = float4(input.posN, 1.0f); output.tex = input.tex; output.eyeRayN = float4(output.posN.xy, 1.0f, 1.0f);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

または、ピクセルシェーダーで直接、補間されたテクスチャ座標を次のようにNDC空間に変換します（この変換の詳細については、第3章を参照してください）。

 float4 posN; posN.x = (Input.tex.x * 2.0f) - 1.0f; posN.y = (Input.tex.y * -2.0f) + 1.0f;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

NDC空間にピクセルの座標があります-ビューポートに移動する必要があります。 行列のプロパティに基づいて：









この目的のためには、逆投影行列が必要です。 次のようになります。









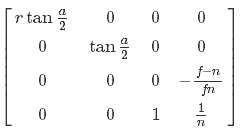
ただし、NDC空間の2次元のポイントを単純に乗算して均一に分割するだけでは不十分です。変換するポイントの深さに関するデータも必要です。 ビュー空間で深度を使用したい-代数変換をいくつか行い、これが可能かどうかを確認しましょう。 まず、種からNDC空間への点の遷移を表現します。









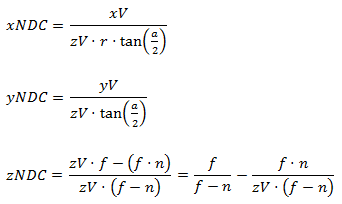
次に、逆射影行列を乗算します。









次に、XとYを単純化し、Wの括弧を展開します。









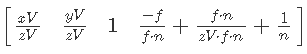
次に、Wの単純化を続けます。











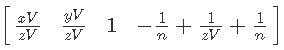
最後の仕上げ-1 / nをカットします。









逆投影行列を掛けた後、結果にビュー空間の深さを掛ける必要があることがわかります。 まず、頂点シェーダーのNDCスペースにデータを準備します。

 output.eyeRayN = float4(output.posN.xy, 1.0f, 1.0f);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、ピクセルシェーダーで主な作業を行います。

 float4 normalDepthData = normalDepthTex.Sample(normalDepthSampler, input.tex); float3 viewRay = mul(input.eyeRayN, invProj).xyz; viewRay *= normalDepthData.w;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ビュー空間に座標があります。 どうぞ

2.レイトレーシング

2.1オフセットデータ



したがって、処理されたピクセルの座標はビュースペースにあります。 次に、これらの座標を持つポイントから、ランダムな方向にN個の光線を配置する必要があります。 残念ながら、HLSL APIには、外部データに関係なく、シェーダープロセス中にランダムまたは擬似ランダムな値を取得できるツールがありません（まあ、またはそのようなテクノロジーの存在については知りません）。したがって、事前にそのようなデータを準備します。 シェーダーでそれらを取得するために、テクスチャを使用する最も簡単な方法。 明らかに、その「重み」とデータ値の制限はピクセル形式に依存します。 私たちの目的には、DXGI_FORMAT_R8G8B8A8_UNORMという形式が非常に適しています。 それでは、サイズを把握しましょう。 おそらく最も簡単で、最も視覚的であると同時に最適ではない方法は、画面解像度に等しい長さと幅のテクスチャを作成することです。 この場合、正方形のテクスチャ座標の値に従ってデータを選択します。これは、（0,0）から（1,1）の範囲にあることを思い出します。 しかし、これらの制限を超えるとどうなりますか？ 次に、D3D11_TEXTURE_ADDRESS_MODE列挙で指定されたルールが作用します。 この場合、D3D11_TEXTURE_ADDRESS_MIRRORの値に関心があります。 このアドレッシングルールの結果を図3に示します。









図3は、D3D11_TEXTURE_ADDRESS_MIRRORを使用した例です。



このアプローチを使用する場合、目的のために差異は許容されます（図4を参照）。









図4-256x256のテクスチャマッピングと0〜1の座標のプリミティブ、および0〜64の座標とD3D11_TEXTURE_ADDRESS_MIRRORのアドレス指定のテクスチャマッピング4x4のプリミティブ



最後に、テクスチャにデータを入力しましょう。 シェーダーでは、テクセルコンポーネントR、G、Bからランダムな方向ベクトルを形成するため、アルファチャネルは使用しません（これは、均一空間のベクトルではゼロであるWのコンポーネントと見なすことができます）。 その結果、コードは次のようになります。

 for(int y = 0; y < texHeight; y++){ for(int x = 0; x < texWidth; x++){ char* channels = reinterpret_cast<char*>(&data[y * texWidth + x]); channels[0] = rand() % 255; //r channels[1] = rand() % 255; //g channels[2] = rand() % 255; //b channels[3] = 0; //a } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、テクスチャのサイズが小さいほど、画像が「きれい」になるという事実にも注意を払いたいと思います（図5を参照）。









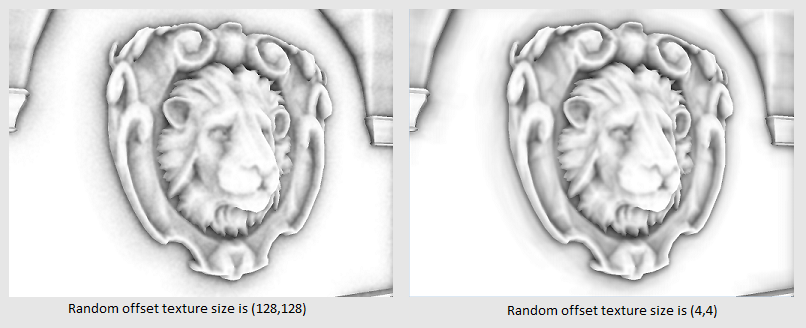
図5-サイズが128x128と4x4のディスプレイスメントのテクスチャの違いのデモ



さて、テクスチャの準備ができました。残っているのは、このデータをシェーダーで取得することだけです。 ただし、0〜1のテクスチャ座標があり、0〜Nの座標を使用する必要があることを思い出してください。N> 0です。この問題は、シェーダー準備の段階で非常に簡単に解決されます。テクスチャが画面全体を占めるようにテクスチャの幅をどのくらい掛ける必要があるか。 画面解像度が1024x468で、テクスチャサイズが2x4であると仮定すると、次のようになります：









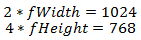
次に、係数を表現します。









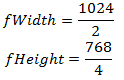
その結果、次のコードを取得します。

 float2 rndTexFactor(fWidth, fHeight); float3 rndData = tex.Sample(randomOffsetsSampler, input.tex * rndTexFactor).rgb;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

おそらく、あなたの場合、ディスプレイスメントテクスチャからの選択のこれらの座標を頂点データとして保存し、それによって既製の補間値を取得する方が合理的です。



さらに、フォーマットDXGI_FORMAT_R8G8B8A8_UNORMを選択したため、オフセットは0〜1のスペースにあります（スペース（-1、1）に移動します（変換の詳細については、第3章を参照）。

 rndData = normalize(2.0f * rndData - 1.0f);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

変位ベクトルができました！



2.2変位ベクトルのカーネル



1つのベクトルは確かに優れていますが、N個のベクトルを起動する必要があります。 0からNの範囲でテクスチャ座標のシフトの特定の要因を取得し、次のようなことを行うことができます。

 for(int i = 0; i < N; i++){ float3 rndData = tex.Sample(randomOffsetsSampler, input.tex * rndTexFactor + Offset * i).rgb; rndData = normalize(2.0f * rndData - 1.0f); /*...*/ }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このオプションはリソースを集中的に使用します。 テクスチャからサンプルを1つだけ使用して、許容できる結果を得ようとします。 私たちの目標は、処理されたピクセル内と隣接するピクセルの両方で、比較的不均一なベクトル分布を実現することです。 事前に準備されたN個のランダムベクトルを使用してみましょう。これらの各ベクトルは、特定の数学的操作で変位ベクトルに適用できます。 これを「変位ベクトルのコア」と呼びます。 確かに、これは私が説明したよりも簡単です）



コアを準備します。

 std::vector<D3DXVECTOR4> kernel(KernelSize); int i = 0; for(D3DXVECTOR4 &k : kernel){ kx = Math::RandSNorm(); ky = Math::RandSNorm(); kz = Math::RandSNorm(); kw = 0.0f; D3DXVec4Normalize(&k, &k); FLOAT factor = (float)i / KernelSize; k *= Math::Lerp(0.1f, 0.9f, factor); i++; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

各コンポーネントの値は-1〜1で生成されます。ベクトルは単位長ではないことに注意してください。 これは、最終画像に大きな影響を与えるため重要です。 図 図6は、投影されたときの非単位長ベクトルがより集中したポイントのセットを形成することを示しています。









図6-非単位長さのベクトルの投影は、より集中したポイントのセットを形成します。 より明確にするために、正射影が使用されます。



さて、カーネルの準備ができました-シェーダーで使用するために残っています。 数学的な操作として、「ベクトルの反射」を使用することにしました。 このツールは非常に便利で、広く使用されています。たとえば、鏡面照明を計算するときに光源に反射ベクトルを取得する必要がある場合、またはボールが壁から跳ね返る方法を調べる必要がある場合です。 反射ベクトルの計算式は次のようになります。









ここで、vは反射するベクトル、nはベクトルの反射に相対的な表面の法線です（図7を参照）









図7-反射ベクトル式の視覚化



ベクトルで最後に行う必要があるのは、法線によって方向付けられた半球内にあることを確認することです。 これを行うには、法線とのスカラー積がゼロより小さい場合に方向を変更します。 その結果、次のコードが得られました。

 //float3 kernel[N] -    //normalV -      float3 rndData = tex.Sample(randomOffsetsSampler, input.tex * rndTexFactor + Offset * i).rgb; rndData = normalize(2.0f * rndData - 1.0f); for(int i = 0; i < N; i++){ float3 samplingRayL = reflect(kernel[N], rndData); samplingRayL *= sign(dot(samplingRayL, normalV)); /*...*/ }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Reflect（）操作の結果は正規化されないことに注意してください。

3.ビームからスクリーン上のポイントまで

振り返って何が起こったのか見てみましょう。 だから：

• 深度データを使用して、フォームの空間内のピクセルの座標を取得しました
• 互いにランダムに分布するN本の光線を得ました。

これで、最終的に私たちの周りにあるものを見つけるために必要なものがすべて揃いました。 続けましょう。 特定のocclusionRadiusスカラーでベクトルを乗算し、ビュー空間のピクセルのポイントに追加します。 アーティストにocclusionRadius値を調整させるのが賢明です。

 //viewRay -      float3 samplingPosV = viewRay + (samplingRayL * occlusionRadius);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

正式に言えば、ビュースペースで、samplingPosVポイントを取得しました。これは、samplingRayL方向のピクセルからある程度の距離にあります。 次に、深さを考慮するために「均一な分割」を行うことを忘れずに、結果のポイントをスクリーンに投影します。

 float4 samplingPosH = mul(float4(samplingPosV, 1.0f), proj); float2 samplingRayN = samplingRayH.xy / samplingRayH.w;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

私たちはNDCスペースにいます。 次に、テクスチャ座標空間に移動する必要があります。 これを行うには、ポイントを-1から1の値の範囲から0から1の領域に変換します。Y軸は反対方向に向けられていることに注意してください。 （図8を参照）









図8-NDCおよびテクスチャ座標空間の座標軸のデモンストレーション



一般に、この種の1次元変換は次のように実行できます-最初に範囲の最小値を減算し、次に範囲の幅（最大値から最小値）で除算し、結果の係数に新しいスペースの範囲の幅を掛けて、結果に加算します新しいスペースの最小値。 言うよりも、これは簡単です。 このケースでは、NxがNDC空間のX座標であり、Txがテクスチャ座標空間のX座標であると仮定します。 次のことが判明しました。









NDC空間のY座標は反対方向に向けられているため、少し異なる動作をする必要があります。 すぐに許容範囲を超えてしまうため、反対の符号を持つ値を取ることはできません。 うーん...画面の右下隅にある点を想像してください-NDC空間では座標は（1、-1）になり、テクスチャ座標空間では-（1、1）になります。 ここで、左上隅のポイントを想像してください-そのNDC空間では座標は（-1、1）になり、テクスチャの座標空間では（0、0）になります。 次のパターンが現れます。境界領域では、Yは1つの座標系で最大値、別の座標系で最小値、およびその逆を想定します。 したがって、係数を取得すると、それを1から減算します。









この問題は別の方法で解決できます。 ソリューションは付録1に示されています。



その結果、シェーダーで次のコードを取得します。

 float2 samplingTc; samplingTc.x = 0.5f * samplingRayN.x + 0.5f; samplingTc.y = -0.5f * samplingRayN.y + 0.5f;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次のように、1つのマトリックスで変換をテクスチャ座標と投影と組み合わせることができることを追加します（Pは投影マトリックスです）。

4.深度データの操作

ほんの少しだけ！ 急いで！ 前の段落で取得した座標に基づいて、データを使用してテクスチャから選択を行います。

 float sampledDepth = normalDepthTex.Sample(normalDepthSampler, samplingTc).w;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

深度データはコンポーネントwに保存されます。 そして...そして、我々は彼らと何をしますか！？ 考え直してみましょう。 ビューのスペースにいます-Z軸はカメラの方向と一致しています。 したがって、得られる深度が小さいほど、オブジェクトは私たちに近くなります。 ビュー空間内のピクセルからある距離にある点を投影したことを思い出させてください。 テクスチャは、ビュースペースの深さも保存します。 テクスチャの深さとポイントの深さを比較すると、何がわかりますか？ テクスチャの深度値がポイントの深度よりも小さい場合、何かがカメラに近くなり、ポイントが表示されなくなります。したがって、この「何か」よりもカメラに近い場合、ポイントが表示されます。 ところで、ShadowMappingはほぼ同じように機能します。 車で複雑な操作を行う必要があり、下から何が起こっているかわからない場合に、動きを調整するように友人に依頼するようなものです。 しかし、彼は酔っていて、あなたが期待したものと反対のデータをあなたに話すのは非常に面白いだろうと思った...しかし、これは私たちの場合ではありません



したがって、カメラから見えるNセットのポイントが少ないほど、ピクセルが受け取る拡散光は少なくなります。 状況を少し異なる方法で考えることができます-ピクセルからその法線の方向を見ると想像してみましょう（光線は法線によって方向付けられた半球内に分布しているため）。 カメラに見えるNセットのポイントが少ないほど、ピクセルから見ることができるシーンオブジェクトの数が少なくなります（シーンオブジェクトの「ジオメトリ」が増えてビューがブロックされるため）。したがって、シーンの散乱光へのアクセスが少なくなります（くそっ！あなたのスキーで「鉄の乙女」！ピカチュウ！私はあなたに挑戦!!）



また、シーンの特定のオブジェクト（取得した深度）が、ピクセルポイントへの散乱光へのアクセスに影響を与えないようにできることも考慮する必要があります（図9を参照）。









図9-ポイントqはカメラに近いですが、ピクセルPのポイントから離れすぎているため、その照明に影響を与えることはできません。



1を追加するだけでなく、距離に応じて特定の係数を追加することをお勧めします。

 float distanceFactor = (1.0f - saturate(abs(viewRay.z - sampledDepth) / occlusionRadius)) * harshness;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

距離係数は、投影したポイントではなく、ピクセルポイントの深さに基づいて形成されます。目の前に何かがあるかどうかを理解するために使用しました。それは私たちからです。 また、粗さパラメーターを使用して強度を調整する機能も追加しました。



一般に、これはアルゴリズムの主要部分であり、いわば、すべての核心です。 変位ベクトルを操作するサイクル全体を見てみましょう。

 //viewRay -      //normalV -      //float3 kernel[N] -    //offset -   ,    float totalOcclusion = 0.0f; [unroll] for(int i = 0; i < 16; i++){ float3 samplingRayL = reflect(kernel[i].xyz, offset); samplingRayL *= sign(dot(samplingRayL, normalV)); float3 samplingPosV = viewRay + (samplingRayL * occlusionRadius); float4 samplingPosH = mul(float4(samplingPosV, 1.0f), proj); samplingPosH.xy /= samplingPosH.w; float2 samplingTc; samplingTc.x = 0.5f * samplingPosH.x + 0.5f; samplingTc.y = -0.5f * samplingPosH.y + 0.5f; float sampledDepth = normalDepthTex.Sample(normalDepthSampler, samplingTc).w; if(sampledDepth < samplingPosV.z){ float distanceFactor = (1.0f - saturate(abs(viewRay.z - sampledDepth) / occlusionRadius)); totalOcclusion += distanceFactor * harshness; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果を見てみましょう！









「ねえ！ 一体何だ！ そして、ここにFarCryはありますか？！」 「落ち着いて！」-あなたに答えます。 「チップとデールは助けを急いでいます！」ああ、これはその記事からではありません-「ブラーは助けを急いでいます！」

5.ぼかしを使用する

5.1最も簡単なオプション



ぼかし効果、またはぼかしは、グラフィックスの多くの領域で使用される非常に便利なツールです。 私はそれを電気テープと比較します（青！これは重要です）-それは何かを修正または改善するために使用できますが、キャビネットの高さからタイルの上に落ちた電話を修正することはほとんど不可能です（「断熱材をラップし、すべてがうまくいく」 「複数回会った）。



効果の本質は簡単です：各テクセルについて、その隣接色の算術平均を取得します



したがって、P座標を持つテクセルがあるとします-R領域（AreaHeightピクセルごとのAreaWidth）の隣接する色の算術平均を計算しましょう。 このようなもの（私は意図的に配列の範囲外をチェックしません。これについては以下）：

 D3DXCOLOR **imgData = ...; //  D3DXCOLOR avgColor(0.0f, 0.0f, 0.0f, 0.0f); for(INT x = Px - AreaWidth / 2; x <= Px - AreaWidth / 2; x++) for(INT y = Py - AreaHeight / 2; y <= Py - AreaHeight / 2; y++) avgColor += imgData[x][y]; avgColor /= AreaWidth * AreaHeight;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

5.2ガウスフィルター



次に、これを行ってみましょう-各隣接の色に、AreaWidth x AreaHeightの次元を持つマトリックスの値を乗算します。 また、すべての行列要素の合計が1に等しくなるようにします。これにより、算術平均加重の特殊なケースになるため、領域のサイズで除算する必要がなくなります。 このようなマトリックスは正式には「畳み込みマトリックス」と呼ばれ、「コア」とも呼ばれ、その要素は「重み」と呼ばれます。 なぜこれが必要なのですか？ したがって、より多くの可能性があります-重みの値を制御することにより、例えば、脈動や緩やかなぼかしの効果を達成できます。 畳み込み行列に基づいたフィルターファミリもあります-シャープニングフィルター、メディアンフィルター、侵食フィルター、およびビルドアップです。



最も一般的なぼかしフィルターは、ガウスフィルターです。 その重要な特性は線形分離性です。これにより、最初に行の入力画像をぼかし、次に列の行の画像をぼかし、1次元フィルターの値で1サイクルを実行できます。









xは-AreaWidth / 2からAreaWidth / 2までの整数です。qはいわゆる「ガウス分布の標準偏差」です



フィルターマトリックスを形成する関数を実装しました。

 typedef std::vector<float> KernelStorage; KernelStorage GetGaussianKernel(INT Radius, FLOAT Deviation) { float a = (Deviation == -1) ? Radius * Radius : Deviation * Deviation; float f = 1.0f / (sqrtf(2.0f * D3DX_PI * a)); float g = 2.0f * a; KernelStorage outData(Radius * 2 + 1); for(INT x = -Radius; x <= Radius; x++) outData[x + Radius] = f * expf(-(x * x) / a); float summ = std::accumulate(outData.begin(), outData.end(), 0.0f); for(float &w : outData) w /= summ; return outData; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

半径5を使用し、偏差は5の2乗です。



5.3シェーダーとそれに関連するすべて



2つのテクスチャを使用します。1つはソースデータを使用し、もう1つは中間結果を保存するために使用します。 画面解像度とピクセル形式DXGI_FORMAT_R32G32B32A32_FLOATに対応するサイズで両方のテクスチャを作成します。 もちろん、品質をあまり落とすことなく、テクスチャのサイズを小さくすることはできますが、この場合、私はそうしないことにしました。 次のスキームに従ってテクスチャを操作します。

 //    { //     } //      { //       }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

前と同様に、NDC空間の四角形を操作します。これは、画面領域全体を占め、テクスチャ座標は0〜1です。今度は、テクスチャの境界を越える処理方法を考えます。



シェーダーコードに直接チェックを実装すると、リソースを大量に消費します。先ほど言ったように、この場合、D3D11_TEXTURE_ADDRESS_MODE列挙で指定されたルールが有効になります。ルールD3D11_TEXTURE_ADDRESS_CLAMPは私たちに適しています。次のことが起こります-各座標は範囲[0、1]に制限されます。つまり、座標（1.1、0）を選択すると、座標（1、0）のテクセルデータが取得され、座標（-0.1、0）を選択すると、（0、0）のデータが取得されます。 Yについても同様です（図12を参照）。









図12フィルターのサイズに関連したD3D11_TEXTURE_ADDRESS_CLAMPのデモンストレーション



最後に知る必要があるのは、テクスチャ座標空間で1ピクセルを移動するためにどれだけ前進する必要があるかです。この問題は簡単に解決されます-画面の解像度が1024 x 768ピクセルであるとしましょう左上隅から-（1 / 1024、1 / 768）。この問題の解を方程式の形で表現することもできます。 （Sx、Sy）を開始位置とし、（Ex、Ey）終了位置とし、「SからEに移動するには画面のどの部分を移動する必要がありますか？」という質問に対する答えを次のようにします。











画面の左上隅から1ピクセル移動したい場合、方程式は次のようになります。









Fの表現と取得：









これで、おそらく、ピクセルシェーダーのコードを取得できます。

 cbuffer Data : register(b0) { float4 weights[11]; float2 texFactors; float2 padding; }; cbuffer Data2 : register(b1) { int isVertical; float3 padding2; }; struct PIn { float4 posH : SV_POSITION; float2 tex : TEXCOORD0; }; Texture2D colorTex :register(t0); SamplerState colorSampler :register(s0); float4 ProcessPixel(PIn input) : SV_Target { float2 texOffset = (isVertical) ? float2(texFactors.x, 0.0f) : float2(0.0f, texFactors.y); int halfSize = 5; float4 avgColor = 0; for(int i = -halfSize; i <= halfSize; ++i){ float2 texCoord = input.tex + texOffset * i; avgColor += colorTex.Sample(colorSampler, texCoord) * weights[i + halfSize].x; } return avgColor; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここでは特別なことは何も起こらないため、頂点シェーダーはここでは引用しませんでした-データをさらに「転送」します。私たちが得たものを見てみましょう：









図13エッジを考慮しないぼかしのデモ



悪くはありませんが、今度はぼやけた顔の問題を解決する必要があります。私たちの場合、これは一見思われるよりも簡単です-結局のところ、必要なデータはすべて揃っています！画面スペースにいる場合、通常データと深度データの急激な変化を追跡するのに十分です。法線のスカラー積または隣接し処理されたピクセルの深さの差の絶対値が特定の値よりも大きいか小さい場合、処理されたピクセルはフェースラインに属すると仮定します。エッジを黄色で強調表示する小さなシェーダーを作成しました。操作の原理はぼかしの場合と同じです。最初に垂直方向に、次に水平方向に渡します。方向に応じて、左右の2つの隣人、または上下の2つの隣人を比較します。次のような結果になりました。

 bool CheckNeib(float2 Tc, float DepthV, float3 NormalV) { float4 normalDepth = normalDepthTex.Sample(normalDepthSampler, Tc); float neibDepthV = normalDepth.w; float3 neibNormalV = normalize(normalDepth.xyz); return dot(neibNormalV, NormalV) < 0.8f || abs(neibDepthV - DepthV) > 0.2f; } float4 ProcessPixel(PIn input) : SV_Target { float2 texOffset = (isVertical) ? float2(0.0f, texFactors.y) : float2(texFactors.x, 0.0f); float4 normalDepth = normalDepthTex.Sample(normalDepthSampler, input.tex); float depthV = normalDepth.w; float3 normalV = normalize(normalDepth.xyz); bool onEdge = CheckNeib(input.tex + texOffset, depthV, normalV) || CheckNeib(input.tex - texOffset, depthV, normalV); return onEdge ? float4(1.0f, 1.0f, 0.0f, 1.0f).rgba : colorTex.Sample(colorSampler, input.tex) ; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

顔の選択を示す図14.



ぼかしの際にこれをどのように使用しますか？とても簡単です！私たちは、色が考慮されるピクセルから非常に遠くにある、または法線方向で著しく異なるそれらの隣の色を考慮しません。ここで、結果を処理済みの重みの合計で割る必要があります。コードは次のとおりです。

 float4 ProcessPixel(PIn input) : SV_Target { float2 texOffset = (isVertical) ? float2(0.0f, texFactors.y) : float2(texFactors.x, 0.0f); float4 normalDepth = normalDepthTex.SampleLevel(normalDepthSampler, input.tex, 0); float depthV = normalDepth.w; float3 normalV = normalize(normalDepth.xyz); int halfSize = 5; float totalWeight = 0.0f; float4 totalColor = 0.0f; [unroll] for(int i = -halfSize; i <= halfSize; ++i){ float2 texCoord = input.tex + texOffset * i; float4 normalDepth2 = normalDepthTex.SampleLevel(normalDepthSampler, texCoord, 0); float neibDepthV = normalDepth2.w; float3 neibNormalV = normalize(normalDepth2.xyz); if(dot(neibNormalV, normalV) < 0.8f || abs(neibDepthV - depthV) > 0.2f) continue; float weight = weights[halfSize + i].x; totalWeight += weight; totalColor += colorTex.Sample(colorSampler, texCoord) * weight; } return totalColor / totalWeight; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次のようになりました：

6.予期しない変更

この記事の作業を終えると、別のテストの結果、オーバーラップの結果がカメラの方向に対して不安定であることがわかりました。これを修正するには、処理されたピクセルの座標とアイテム3のポイントをビュースペースからワールドに変換する必要があります。私の場合、すべての重要なデータをビュースペースに格納するという事実が問題を複雑にしているため、すべてのレイのループで、ポイント深度をビュースペースに変換するか、テクスチャからワールドスペースに深度を変換する必要があります。また、法線をワールド空間に変換することを忘れないでください。ただし、サイクルに依存しないため、それほど重要ではありません。

7.結論

私の記事に注目してくれた読者に感謝したいと思います。そして、そこに含まれる情報が彼にとって利用可能であり、興味深く有用であることを願っています。Leonid ForhaxeDの記事にも感謝したいと思います -私はそれから多くを取り、それを改善しようとしました。



サンプルのソースコードはgithub.com/AlexWIN32/SSAODemoからダウンロードできます。例全体または個々のサブシステムとしての操作に関する提案やコメントは、メールで送信するか、コメントとして残すことができます。成功を祈っています！