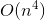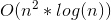ボロノイ図とその応用

一日中良い、サイトHabrahabrの親愛なる訪問者。 この記事では、ボロノイ図（下の図を参照）、それを構築するためのさまざまなアルゴリズム（ 、 -半平面の交差、 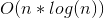-Fortuneのアルゴリズム）および実装のいくつかの微妙な点（C ++で）。







チャートの多くの興味深い応用と、それに関するいくつかの興味深い事実も考慮されます。 面白いでしょう！



記事の概要：



- 必要な概念と定義

- 構築アルゴリズム

- アプリケーション

- 興味深い事実

- 参照



この記事では、平面上にボロノイ図を構築するためのアルゴリズムのみが考慮されることに注意してください。 途中で、ダイアグラムの作成に必要な他のアルゴリズムを検討します。2つのセグメントの交点を決定するアルゴリズム、2つの凸多角形を交差させるO'Rourkeアルゴリズム、および「海岸線」を作成するアルゴリズムです。

必要な概念と定義

次に起こることはすべて 飛行機上にあるとすぐに言わなければなりません。



さて、これが何であるかを理解する前に-ボロノイ図、私たちが必要とする幾何学オブジェクトのいくつかの概念を思い出させます（ただし、点、線、光線、線分、多角形、頂点、多角形のエッジの定義に既に精通していると仮定します、平面を分割するベクトルおよび直感的な概念）：



単純なポリゴンとは、自己交差のないポリゴンです。 単純なポリゴンのみを検討します。



非凸多角形とは、2つの頂点が存在する多角形のことで、これらの頂点を結ぶエッジを除き、指定された多角形と交差する線が描かれます（図を参照）。



凸多角形とは、辺の延長線が他の辺と交差しない多角形です（図を参照）。 他の定義はウィキペディアで利用可能です。









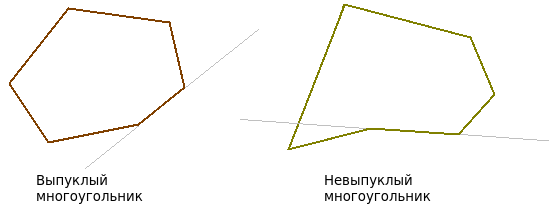
ダイアグラムを構成するのは凸多角形です。 なぜ凸から正確に？ それらは凸面図形である半平面の交点（後で見る）にすぎないため、凸面図形の交点が凸面図形である理由はここにあるので、自分で確かめることをお勧めします（証拠は、たとえば本[2]にあります ）。



半平面について話し始めたので、ダイアグラム自体（いわゆる軌跡からなる）にスムーズに移動できます。この領域では、他のすべてのポイントよりも特定のポイントに近いポイントがすべてあります。 ボロノイ図では、軌跡は凸多角形です。



軌跡を作成する方法は？ 定義により、次のように構築されます。n個のポイントのセットを与えて、ダイアグラムを構築します。 軌跡を構成する特定のポイントpと 、与えられたセットの別のポイント-q （ pと等しくない）を取ります。 これらの2つのポイントを結ぶ線を描画し、このセグメントの中央の垂線となる線を描画します。 この線は平面を2つの半平面に分割します。1つは点pで、もう1つは点qです。 この場合、これらの2点の軌跡は、結果の半平面です。 つまり、点pの軌跡を構築するには、そのようなすべての半平面の交点を取得する必要があります（つまり、 qを除く特定のセットのすべての点がqの代わりになります）。









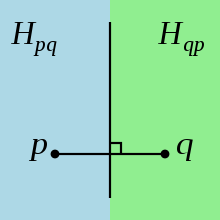
軌跡が構築されるポイントは、 サイトと呼ばれます 。 次の図では、軌跡は異なる色でマークされています。









ダイアグラムを構築するためのアルゴリズムは、特定のセットのすべてのポイントに対してこれらの同じ軌跡を構築するためのアルゴリズムに他なりません。 この問題の軌跡は、 ボロノイポリゴンまたはボロノイセルとも呼ばれます 。



最後に、平面上のn点のボロノイ図の定義を定式化します（nは正の整数）-これは、 n軌跡 （軌跡ごとの各点）で構成される平面のパーティションです 。 繰り返しになりますが、別の定義はWikipediaにあります。



ちなみに、ここはボロノイ図のインタラクティブなカラービジュアライザーを備えたサイトです。 自分で領域をクリックして、図の作成方法を確認することができます。



ダイアグラムがどのように表示され、なぜボロノイという名前が付けられているのかに興味がある場合は、以下のネタバレをご覧ください。

構築アルゴリズム

ボロノイ図の作成方法を学びます。 4つのアルゴリズムを検討します。そのうち2つは詳細です（1つは実装あり、別の記事ではFortuneのアルゴリズムの完全な実装に専念します）。

1. 「額に」ボロノイ図をプロットするためのアルゴリズム。 難易度： ;
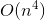2. 半平面を交差させてボロノイ図を作成するアルゴリズム。 難易度： ;
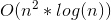3. 平面上にボロノイ図を作成するためのフォーチュンのアルゴリズム。 難易度： ;
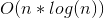4. 再帰的ボロノイ線図プロットアルゴリズム。 難易度： 。

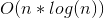いくつかのアルゴリズムの説明の後、C ++での実装が提供されます。 実装には、私たちが作成したライブラリSplashGeom©-github へのリンクを使用しました。これには、平面上および空間内のいくつかの計算ジオメトリのアルゴリズムを実装するために必要なすべてが含まれています。 このライブラリを厳密に判断しないようお願いします。まだ活発な開発と改善の段階にありますが、すべてのコメントが聞かれます。



他の実装に興味がある場合は、次のとおりです。

• boost.polygon
• Steve FortuneのWebサイト
• オーリン/オープンボロノイ
• Java実装
• JavaScriptでの実装（ビジュアライザーもあります）

それでは、アルゴリズムの直接調査に移りましょう。

「額に」ボロノイ図を構築するためのアルゴリズム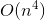

ここでのアイデアは、半平面を横切るのではなく、セグメントの中央の垂線を（これは簡単で、同意するため）交差させ、この点を他のすべての点と接続することです。 つまり、ボロノイセルの定義に従って、次のように点pの軌跡を作成します。

1. このポイントpを他のセグメントと接続するすべてのセグメントの中央の垂線を描いたので、n-1の直線（中央の垂線）を取得します。
2. すべての線をペアで交差させて、 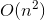交差点（「最悪の場合」では、各直線が他のすべての直線と交差できるため）;
3. これらすべてを確認してください 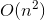n-1個の半平面のそれぞれのメンバーシップ上のポイント、つまり、漸近線をすでに取得している 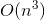。 したがって、すべての半平面に属するポイントは、ポイントpのボロノイセルの頂点になります。
4. すべてのnポイントに対して最初の3つのステップを実行し、結果の漸近を取得します 。

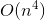アルゴリズムはe-maxx.ruにもあります。



必要に応じて、SplashGeom©を使用してこのアルゴリズムを個別に実装できます。 この記事では、このアルゴリズムは実際には少なくとも以下のものよりはるかに劣るため、その実装は示されていません...

半平面を超えて交差することによりボロノイ図を構築するためのアルゴリズム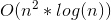

このアルゴリズムは、それほど複雑な計算を必要としないため、すでに実際に使用できます。 そのためには、セグメントとラインを交差させ、凸多角形を交差させ、半平面を交差させ、得られた軌跡をダイアグラムに結合できる必要があります。

アルゴリズム

1. 現在のサイトのn-1直線を取得します（前のアルゴリズムのように-中央の垂線）。 これらは、半平面の「ジェネレータ」になります。
2. これで、n-1半平面ができました。 これらの各半平面は、前からの直線で与えられます。 ポイントと方向、つまり、線のどちら側にあるか。 方向は、軌跡を構築する現在のサイトによって決定されます。これは、目的の半平面にあるため、軌跡はその中になければなりません。
3. 私たちはすべての半平面を横断します-私たちはそれをすることができます 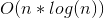-現在のサイトの軌跡を取得します。
4. すべてのnポイントに対して最初の3つのステップを実行し、結果の漸近を取得します * = 。

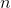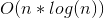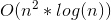実装

ここでの主なキャッチは、凸多角形の通常の交差を実装することです、なぜなら、不快な縮退ケースがあるためです（多角形の頂点および/または側面が一致します。多角形がそれ自体と交差する場合、この場合）。



アクションの範囲全体を外接する長方形に制限していることをすぐに言わなければなりません-ハーフプレーンは互いに交差する部分を切り取ります。 これにより、ダイアグラム内の無限セルの問題が解決されます。

線と線分の交点

そして、その存在の判断だけでなく、正確に交点が必要です。 SplashGeom©では、これは-たとえば、ラインとセグメントの交差の実装です。

凸多角形の交差

これで、ポリゴンの交差が実現しました。 もちろん、あなたはそれをすることができます 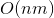ここで、nとmはそれぞれ1番目と2番目の多角形の頂点の数です-最初の多角形の各辺と2番目の多角形の各辺を交差させ、交差点を書き込み、さらに別の多角形に属する点を確認しますが、より良い速度を達成するために、アルゴリズムに従って交差しますO`Rourke（アルゴリズムの元の説明- [3] ）。



また、その説明のオプションの1つはalgolist.ruにあります。 私たちの場合、実装は、いくつかの補足的なアイデアとともに、本[1] （p。334）のアルゴリズムの説明に基づいています。 この実装では 、ポリゴンに共通の辺が ある場合（本[1]に記載されているように、この場合は別途考慮する必要があります）を考慮していませんが 、共通の頂点を持つ場合は正しく機能します。



以下のネタバレの下に、アルゴリズムの一般的な説明があります。





さて、SplashGeom©では次のようになります。





この説明とコードが役に立つことを願っています。

半平面の交差点

したがって、半平面の交差点を構築するために必要なものはすべて揃っています。 さて、それをやってみましょう、そしてそれだけでなく、賢い方法で-交差する半平面の操作の結合性のために、任意の順序でそれらを交差させることができます。つまり、2つの平面を交差させ、さらに2つの平面を交差させ、次に交差点を交差させます、これはすべてを個別に横断するよりも早くなっています。



そのため、 再帰を使用することをお勧めします（気分はすぐに悪くなりました） -ここでの作業は理解できます。

軌跡をチャートに追加する

これで、指定したポイントのボロノイポリゴンができました。それをダイアグラムに追加します。 領域を任意の順序で取得し、それらは互いに関連していないため、これには特に問題はありません（Fortuneアルゴリズムの実装とは異なり、エッジへのポインターで隣接する軌跡に移動できます）。





そこで、ボロノイ図を作成する方法を学びました 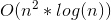、それは軌跡のベクトル（リスト）の形をしています。 このソリューションの欠点は、隣人に関する情報を取得できないことです（おそらく、この欠点は実装を改善することで解消できます）。



さらに多くの情報をRSEL （ DCEL ）から取得できます。 この構造は、Fortuneのアルゴリズムで使用されます。



次に、Fortuneのアルゴリズムを、直線と「海岸線」を使用して説明します（水着と水泳パンツを準備します-ビーチに行きます） 。 私の意見では、これはボロノイ図の構築を実装し、 光の 「速度」で構築したい場合に最も受け入れられるオプションです 。

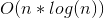のボロノイ図を構築するためのフォーチュンのアルゴリズム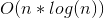

1987年、スティーブフォーチュンは、 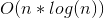。 もちろん、それはそのような漸近線を持つ唯一の構築アルゴリズムではありませんが、非常に理解可能であり、実装するのはそれほど難しくありません（さらに、非常に美しく数学的です！ ）、私はそれを選びました。



フォーチュンアルゴリズムの資料は、 こちら 、 こちら 、 こちら 、 こちらでご覧いただけます 。



ところで、 Habrahabrの記事はすでにこのアルゴリズムの検討に専念しています。



したがって、アルゴリズムの主なアイデアは、いわゆるスイープラインです。 特定のオブジェクトセットに沿った直線の動きを簡単にシミュレートできるため、計算ジオメトリの多くのアルゴリズムで使用されます（たとえば、n個のセグメントを交差させるアルゴリズムでもスイープラインが使用されます）。



どのように、何をするのかについて話を始める前に、スイープラインがどのように動くかを見てみましょう（ ここから ）









いいですね。 実装では、すべてがほぼ同じで、RFPのみが通常、左から右ではなく上から下に移動します。実際、すべてはそれほど滑らかではなく、イベントごとに発生します（以下を参照）。

アルゴリズムの本質

n個のサイト（平面上のポイント）があります。 「上から下へ」、つまり最大の縦座標を持つサイトから小さい座標を持つサイトへ（正確にはイベントからイベントへ）に移動するスイープラインがあります。 すぐに注意する必要があるのは、図の構築に影響を与えるのは、 より高いサイトまたは抜本的なライン上にあるサイトのみ です 。



ZPが次のサイト（ ポイントイベント）に到達すると、新しい放物線（アーチ）が作成されます。このサイトの焦点は 、 ディレクターです（ ウィキペディアの放物線について ）。 この放物線は平面を2つの部分に分割します。放物線の「内側」領域はサイトに近いポイントに対応し、「外側」領域は掃引線に近いポイントに対応し、放物線上にあるポイントはサイトおよびGPから等距離にあります。 放物線は、サイトへのRFPの位置に応じて変化します。RFPがサイトからさらに下がれば下がるほど、放物線は拡大しますが、最初は一般にセグメントです（「上向き」）。



放物線が拡大すると、2つのブレークポイントがあります。他の放物線との交点（「海岸線」）です。 「海岸線」には、交差点の1つのポイントから他のポイントまでの放物線状の円弧が格納されているため、ビーチラインが判明します。 実際、このアルゴリズムでは、この「海岸線」の動きをシミュレートします。 これらの同じブレークポイントはボロノイセルのエッジに沿って正確に移動するためです（結局、コントロールポイントはこれらの放物線が対応する両方のサイトから、さらにはRFPからも等距離であることがわかります）。



そしてちょうどその瞬間、異なる放物線の1つにある2つの制御点が「会う」とき、つまり1つに変わるかのように、この点がボロノイセルの頂点になります（円イベントが発生します）。この時点で、これらの2つのポイントの間にあった円弧-「崩壊」し、「海岸線」から削除されます。 次に、このポイントを前の対応するポイントに接続し、ボロノイセルのエッジを取得します。

アルゴリズム

そのため、スイープラインを下に移動すると、2 種類のイベントが発生します 。

ポイントイベント

ポイントのイベントは、サイトの1つでのPOのヒットです。そのため、このサイトに対応する新しい放物線を作成し、2つのブレークポイントを追加します（実際、最初は1つですが、アーチを拡張すると、すでに2つあります）-この交差点海岸線のある放物線（つまり、既存の放物線の前面）。 このアルゴリズムでは、放物線（またはむしろ「海岸線」に属する部分- アーチ ）は、ポイントイベントの場合にのみ 「海岸線に挿入」されます。つまり、新しいアーチはポイントイベントの処理時にのみ表示されます。



ところで、次の写真は、なぜこのような「放物線のかけら」の関連が「海岸線」と呼ばれるのかを示しています。

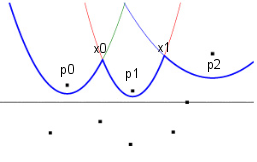
サークルイベント

サークルイベントは、1つのアーチの削除に伴うボロノイセルの新しい頂点の出現です。ここでのダイアグラムの新しい頂点の出現は、アーチの左右の点と新しい頂点のアプローチにより、左、中央、右、中央の「崩壊」の3つのアーチがあったことを意味するためですボロノイ図。 このアルゴリズムでは、円イベントが発生した場合にのみ放物線（アーチ）が「海岸線」から削除されます。つまり、アーチは円イベントを処理するときにのみ削除できます。









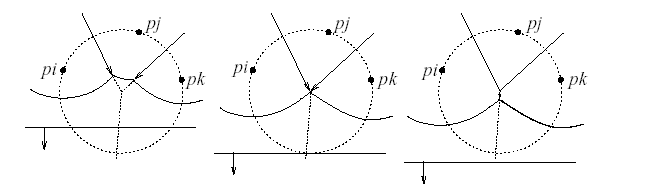
ボロノイ図の頂点は常に図の正確に3つのエッジの交点にあるという定理があり、図の頂点は3つのサイトを通る円の中心であり、この点からスイープ線までの距離も同じであると述べていますこの円の半径に等しい（これは「海岸線」上にあるポイントのプロパティです）。 これは、3つのサイトを通過する円の最下点がスイープラインの下またはスイープライン上にあるときに、この最下点の円イベントをイベントキューにプッシュするためです。ボロノイ図。



イベント（ポイントまたはサークル）では、1つの特定のアーチが接続されていることが重要です。 これは、イベントを処理するときに役立ちます。 また、時間内にRSDS （ DCEL ）にエッジを追加する必要があることを忘れてはなりません（構造内のポイント1、以下を参照）。したがって、アーチとエッジの関係を理解する必要があります。



したがって、線の動きは離散的です。 サイト上の任意の瞬間、 または 3つのサイトを通る円の下部の線で 、その中心はボロノイ図の新しい頂点です。 素晴らしい。



一般的なアルゴリズム ：

1. 最初にポイントイベントで初期化するイベントのキュー（優先順位付き）を作成します-このサイトのセット（結局、ポイントイベントは各サイトに対応します）;
   
   
   
   
2. キューが空ではない間：
   
   
   
   a）。 それからイベントを取ります。
   
   b） これがポイントイベントの場合、ポイントイベントを処理します。
   
   c）。 これがサークルイベントの場合、サークルイベントを処理します。
   
   
   
   
3. 残りのすべてのエッジを仕上げます（border_boxを使用）。

実装

Fortuneアルゴリズムの実装については、別の記事で詳細に検討しますが、ここでは、その理解に役立つ可能性のあるいくつかの開発について説明します。

必要な構造

このアルゴリズムを実装するには、いくつかの構造（クラス）が必要です。

• RSDS （ DCEL ）-すでに見つかったボロノイ図のエッジを保存するためのリスト。
• イベントのある優先キュー。
• バイナリツリー（BeachSearchTreeがあります）-「海岸線」を保存するため-放物線とポイントの現在の位置。 このツリーはバランスが取れていることに注意してください。ノードには正確に2人の息子、またはゼロ（葉）があります。 この構造の詳細については、たとえば、 Habréのこの記事を参照してください （ この国では少し異なって表示されます）。

このようなデータ構造を使用して、一般的なアルゴリズムの実装を作成できます。





HandlePointEvent（）とHandleCircleEvent（）のすべてのロジックと複雑さは、別の記事の主題になります。以降、実装に役立ついくつかの補助関数を示します。

ヘルパー関数

放物線の交差点（アーチ）

RFPの位置に応じて、2つの放物線（アーチ）の交差点を取得できる必要があります。 点x 'およびy'に焦点を当てた放物線の方程式と、y軸に沿った位置がlである直接行列は、次の方程式で与えられます（導出可能）。







ところで、ブラケットの前の部分はこの放物線の焦点パラメータです 。 ここから、放物線方程式の対応する係数を「引き出し」、簡単な方法で2つの非線形方程式を解くことができます。一方から他方を減算し、最初に見つかった根を代入して、2つのポイントを取得します。 最も高いポイントは「海岸線」の背後にあるため、低いポイント（つまり、縦座標が小さいポイント）に興味があります。 説明されたアクションは、次のコードに反映されます。

3点で円を描く

円イベントを処理するとき、3つのアーチ（サイト）の焦点から構成される円の中心と最下点を決定する必要があります。3点を使用して円を構築するためのいくつかの分析アルゴリズムがあります（構築により、その中心と半径を取得することを意味します）、私たちのプログラムではこれが行われます（アルゴリズムのおかげで）-最初の2点と2番目の2点をセグメントで接続します。中心は中央の垂線の交点にあり、半径は中心から3点のいずれかまでの距離です。速くて美しい：

ポイントイベント処理

ポイントイベントは、PointEventをキューから取り出したときです。何が入っているの？このイベントが関連付けられているサイトのみがあります。



それを処理するときに何をしますか？ 「海岸線」に新しいアーチを追加し、ツリーの「必要に応じて」すべての接続を設定し、3つの可能なケースのいずれかでサークルイベントが発生したかどうかを確認します。新しいサイトが参加できるすべてのケースを確認する必要があります。



アーチを追加するときはどうしますか？バイナリの「海岸線」ツリー（x座標）でその場所を探し、それを挿入します。









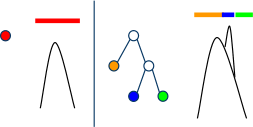
貼り付けたら何をしますか？新しいアーチが2つのポイントで交差するアーチへのポインターを見つけました（交差ポイントがコントロールポイントの1つに正確に当たる場合は個別に考慮されます-交差は2つの放物線-左右にあります）。



つまり、「壊れる」このアーチを取り、代わりに5つのノード（1、5、はい）を挿入します-arch1、bp1、arch2、bp2、arch3。 Arch1は、新しいアーチが交差するアーチの左側部分です。つまり、左のブレークポイントの左にあるピース、bp1は左のブレークポイント（新しいアーチの左の交差）、arch2は新しいアーチ、bp2は右のブレークポイントです（右新しいアーチの交差点）、arch3は、新しいアーチが交差するアーチの正しい部分です。



ポイントイベントがボロノイ図の新しいエッジ（または、エッジがある場合があります）を生成することは注目に値します。



新しい海岸線を「海岸線」に追加するための可能なオプションの1つは、Habréのこの記事で説明されています。

サークルイベントハンドリング

サークルイベントは、キューからCircleEventを引き出したときです。



何が入っているの？その中にポイントがあります-これは、3つのサイトを通過する特定の円の最低ポイントであり、削除すべきアーチです。ツリーには2つのコントロールポイントがあり、彼女自身、コントロールポイントは最終的に1つになります。そして、アーチをツリーから慎重に削除し、すべての「親子関係」を再構築する必要があります。実際、このイベントを処理すると、ツリー内の3つのノードが1つに置き換えられます（2つのブレークポイントと1つのブレークポイントを持つアーチ）。



サークルイベントがボロノイ図の2つのエッジを完了すること、つまり、このイベントが処理されるとエッジが終了することに注意してください。



また、イベント処理の重要な部分は、エッジの成長を監視し、それらをリストに追加してエッジを完成させる方法です。つまり、最終的にはすべて「終了」し、有限であるか、境界に置かれます長方形。

結果の小さな分析

出力ですでにRSDS（DCEL）を受け取るので、十分な情報を取得できます-対応するサイトを知っている各エッジについて、このエッジの「ツイン」を取得し、そのサイトを見つけて、出来上がり-隣人を認識しましたリストに、すべてのサイトの隣人のリストを作成できます。これはすでに達成されています。 + = ）



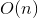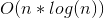さらに、エッジに「ゼロ」サイトがある場合、「境界サイト」、つまり「無限」の軌跡を持つサイトにいます。うーん、しかしこれにより、ポイントの初期セットの凸包を構築することができます; 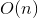最後に、素晴らしい。



まあ、一般に、RSDSは本質的にグラフなので、多くのグラフアルゴリズムでこのリストを引き続き使用できます。

のボロノイ図を作成するための再帰アルゴリズム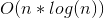

このアルゴリズムは本[1]（p。260）で提供されています。ここでは、Fortuneアルゴリズムとよく似ていますが、このオプションを実装しなかったため、構築アルゴリズムのみを提供します。

アルゴリズム

1. Sサイトのセット全体を2つのほぼ等しい部分（奇数個のポイントがある場合があります）S ₁とS _2に分割します。
2. S ₁およびS _2のボロノイ図を再帰的に作成します。
3. 結果の図を組み合わせて、Sの図を取得します。

アルゴリズムの一般的な説明は複雑ではありませんが、アルゴリズムには独自の微妙な点があります。詳細については、指定された本を参照してください。

用途

ボロノイ図のすべてのアプリケーションの完全なリストはここにあります。私にとって最も興味深いと思われたものをいくつか紹介します（多くの情報は[1]から取得しました）。

プログラミング、ゲーム開発、地図作成

計算幾何学ボロノイ図での問題解決がすべての必要な最初のある近接ポイントを、むしろ、それはのタスクで特別賞チャート与え、すべての最近傍 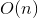（..かかわらず、ない大音量の音楽が含まれたもの）を、同様の方法、それはそう簡単ではありませんので、 （[1]）。ボロノイ図を使用して、背後に凸包を構築できます（「レイ」エッジを見て、それらが属するサイトを見つけ、それらを船体に含めます）。



ボロノイ図とドロネー三角形分割の間にも重要な関係があり、次々に構築することができます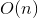彼らはお互いにデュアルなので（ -エッジが隣接サイトは、最終的にドロネー三角形分割取得接続vikikonspektyを）。ゲーム開発で



ボロノイ図を使用する例は、たとえばこの記事にあります。ここでは、ゲームエンジンのナビゲーションシステムは図に基づいています。



さまざまなジオロケーションソフトウェアがボロノイ図を使用する可能性があります。位置情報参照システムは、Voronoiダイアグラムを使用して、たとえば、場所のさまざまな検索と分析のために、最寄りの食料品店を決定できます。







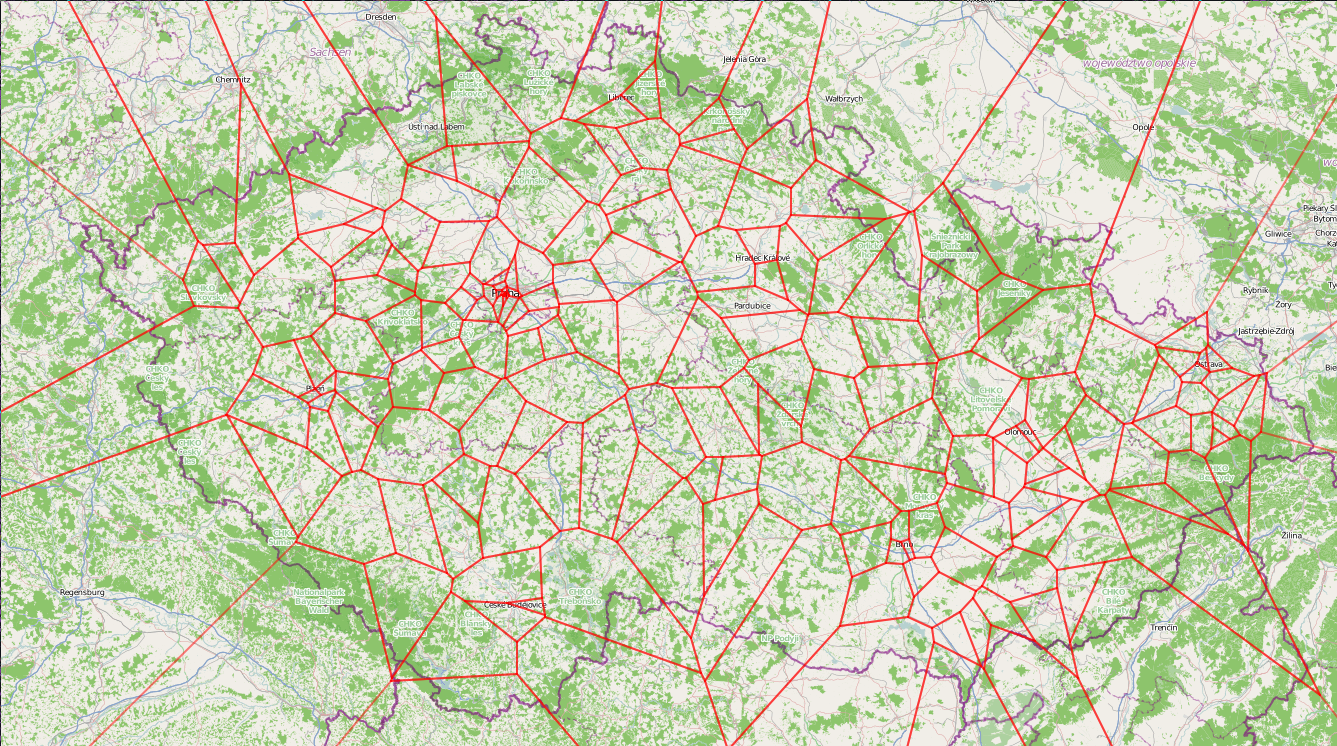
ここでは、地図作成でのチャートの使用に言及することもできます-地域の境界の概要と、それらに基づいたさらなる分析。とにかく、色付きのボロノイ図の助けを借りて、何かの分布を示す地理図を明確に示すことができます。そこには、必要なインジケーター（温度など）の推移が表示されます。









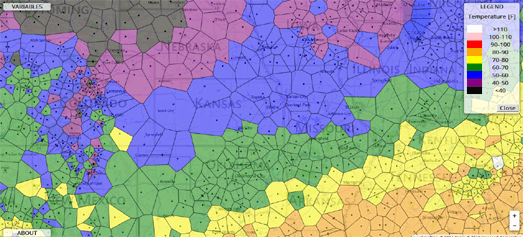
もちろん、Voronoiダイアグラムを使用してさまざまなフィルター写真ハンドラーを作成し、ある種の「モザイク」を作成できます。









しかし、これはアプリケーションの始まりにすぎません。

建築と設計において

ボロノイ図は美しい図形であり、一種の「幾何学的なウェブ」であるため、人々が建築とデザインでボロノイ図を使用するというアイデアを思いついたのは非常に論理的です。すべての作成。 例：

考古学で

[1]から：

考古学では、ボロノイポリゴンを使用して、古代文化のツールの使用範囲をマッピングし、競合する貿易の中心の影響を研究しています。

生態学では、体が生き残る能力は、食物と光のために戦わなければならない隣人の数に依存します。

-これは非常に論理的です。なぜなら、通常、近隣の地域は「生存」のために戦うからです。

モデリングと認識において

この記事では、Voronoiの3Dダイアグラムについては説明しませんが、物理学およびオブジェクトの3Dモデリングに多くの用途があります。空間内のオブジェクトのさまざまな種類のグリッド（およびスケルトン）は、ボロノイ図を使用して構築できます（ただし、より多くの場合、ドロネー三角形分割を使用します）。さまざまなオブジェクトの







3Dスキャン（およびコンピュータービジョン）では、ボロノイ図とドロネー三角形分割も使用できます。また、ロボット工学（障害物を考慮したロボットの動き）と密接に関連しています。

生物学と化学

[1]から：

複雑なボロノイ図が構築される研究のために、電気力と短距離力を組み合わせた影響は、分子の構造を決定するのに役立ちます。

ボロノイ図の使用に関する別の興味深い記事があります。

興味深い事実

自然は驚くべきものです。キリンの色が実際にボロノイ図のように見えることがわかったからです。これは肉眼で見ることができます：









次の観察も注目に値します。これは、樹木の葉の上でも図を見ることができることを示しています。









ちなみに、1年ほど前に、1つの事件がボロノイ図にも関連付けられました。ここでは、新しいモスクワプロジェクトのロゴに使用されました。











そして-最後に-サイト内に中心を持つ円の成長とともに図がどのように表示されるかを見ることができるビデオ：







ここでは、いくつかの火源を持つ火の広がりとの類似性を描くことができます。



さて、誰が自分に最も近いかを知っている世界への私たちの小さな旅行は終わりました。この記事を楽しんで、新しい、便利で面白い何かを本当に学んだことを願っています。



ご清聴ありがとうございました！

参照資料

[1]準備F.、Shaymos M.計算幾何学。はじめに（1989）

[2] Alexandrov A. D.、Werner A. L.、Ryzhik V. I. Stereometry。空間の幾何学

[3]ジョセフ・オルーク。Cの計算幾何学



」この記事は、Institute of Physics and Technologyの1年生であるIlya Zakharkinによって作成されました。

»FIVT MIPT Kirilenko ElenaとKasimova Nadezhdaの1年生も図書館の執筆を手伝いました。

»ライブラリをテストすることで、ヤロスラフ・スピリンを助けました。

»指導者のGadelshin IlnurとGafarov Rustamに特に感謝します。