強化学習とは、システムに関する情報はないが、何らかのアクションを実行できるモデルをトレーニングする機械学習方法です。 アクションはシステムを新しい状態に移行し、モデルはシステムから何らかの報酬を受け取ります。 ビデオに示されている例を使用して、メソッドの操作を検討してください。 ビデオの説明には、 Pythonで実装されているArduinoのコードが含まれています。
挑戦する
強化トレーニング方法を使用して、トロリーに壁から最大距離まで移動するように教える必要があります。 この賞は、移動中に壁からトロリーまでの距離を変更することの価値として表されます。 壁からの距離Dは、距離計によって測定されます。 この例の移動は、2つの矢印S1とS2で構成される「ドライブ」の特定のオフセットでのみ可能です。 矢印は、ガイドが「膝」の形で接続された2つのサーボです。 この例の各サーボは、6つの等しい角度を回転できます。 モデルには4つのアクションを実行する機能があります。2つのサーボの制御です。ステップ0と1は最初のサーボを時計回りと反時計回りに回転させ、ステップ2と3は2番目のサーボを時計回りと反時計回りに回転させます。 図1は、トロリーの実際のプロトタイプを示しています。

図 1.機械学習実験用のトロリープロトタイプ
図2では、矢印S2が赤で強調表示され、矢印S1が青で強調表示され、2つのサーボが黒で強調表示されています。

図 2.エンジンシステム
システム図を図3に示します。壁までの距離はDで示され、距離計は黄色で表示され、システムドライブは赤と黒で強調表示されます。

図 3.システム図
S1およびS2の可能な位置の範囲を図4に示します。

図 4.a. ブーム位置範囲S1

図 4.b. ブーム位置範囲S2
ドライブの制限位置を図5に示します。
S1 = S2 = 5の場合、地面からの最大距離。
S1 = S2 = 0の場合、地面までの最小距離。
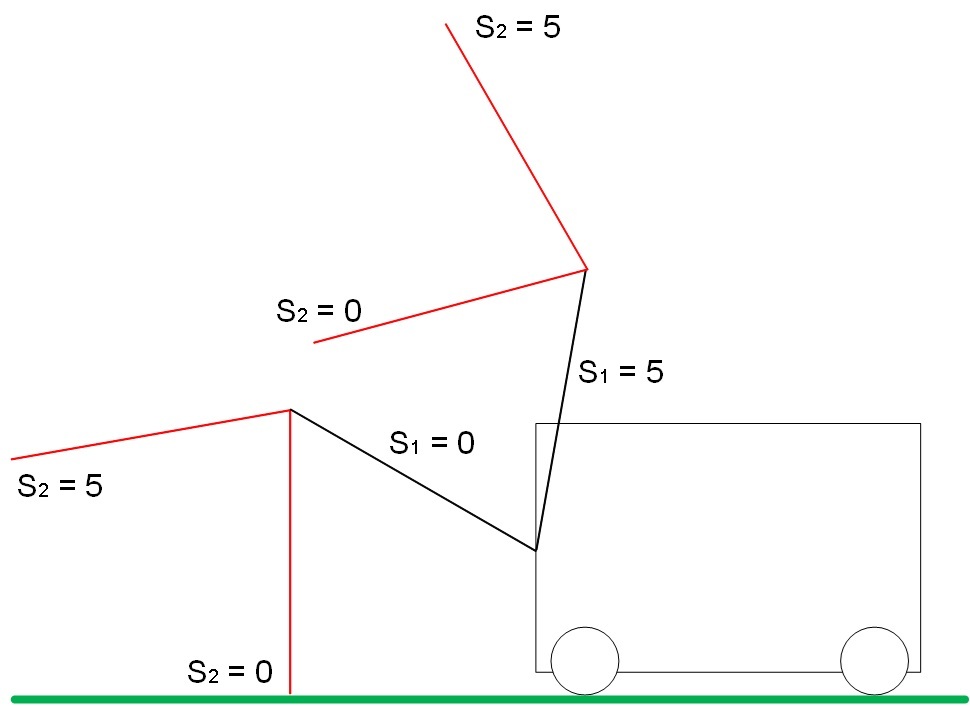
図 5.矢印S1およびS2の境界位置
「ドライブ」には4つの自由度があります。 アクションは、特定の原則に従って、空間内の矢印S1およびS2の位置を変更します。 アクションのタイプを図6に示します。
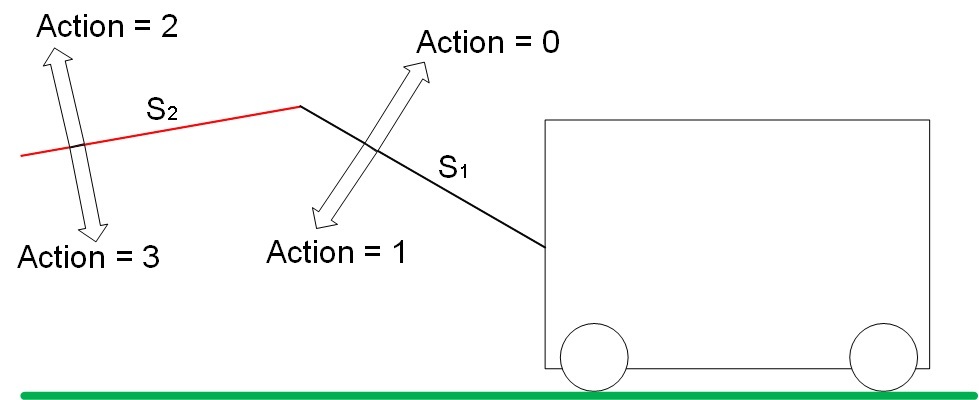
図 6.システム内のアクション(アクション)のタイプ
アクション0は、S1の値を増やします。 ステップ1は、S1の値を減らします。
ステップ2は、S2の値を増やします。 ステップ3は、S2値を減らします。
ムーブメント
このタスクでは、トロリーは2つの場合にのみ駆動されます。
位置S1 = 0、S2 = 1で、アクション3はトロリーを壁から動かし、システムは壁までの距離の変化に等しい肯定的な報酬を受け取ります。 この例では、報酬は1です。
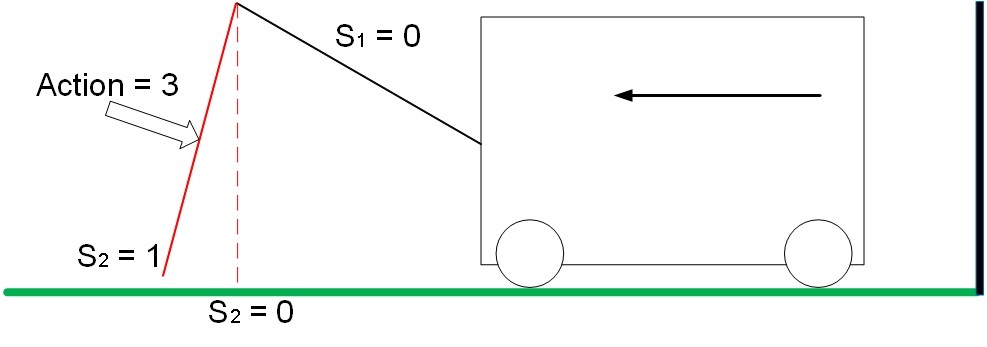
図 7.ポジティブな報酬システムの動き
位置S1 = 0、S2 = 0、アクション2でトロリーを壁に移動すると、システムは壁までの距離の変化に等しい負の報酬を受け取ります。 この例では、報酬は-1です。

図 8.負の報酬システムの動き
他の条件および「ドライブ」のアクションの下では、システムは静止し、報酬は0になります。
システムの安定した動的な状態は、状態S1 = S2 = 0からのアクション0-2-1-3のシーケンスであり、トロリーは最小数のアクションで正の方向に移動することに注意してください。 膝を上げた-膝をまっすぐにした-膝を下げた-膝を曲げた=トロリーが前方に移動した、繰り返した。 したがって、機械学習法を使用して、システムのそのような状態、特定の一連のアクションなどの報酬をすぐに受け取らないことが必要です(アクション0-2-1-報酬は0ですが、次のアクション3で1を取得する必要があります3) )
Q学習方法
Q-Learningメソッドの基礎は、システム状態の重みのマトリックスです。 行列Qは、システムの考えられるすべての状態と、さまざまなアクションに対するシステムの反応の重みのセットです。
この問題では、システムパラメータの可能な組み合わせ36 = 6 ^ 2。 システムの36の状態のそれぞれで、4つの異なるアクション(アクション= 0,1,2,3)を実行できます。
図9は行列Qの初期状態を示しています。ゼロ列には行インデックスが含まれ、最初の行はS1値、2番目はS2値、最後の4列は0、1、2、および3に等しいアクションを持つ重みです。各行はシステムの固有の状態を表します。
テーブルを初期化するとき、重みのすべての値を10に等しくします。
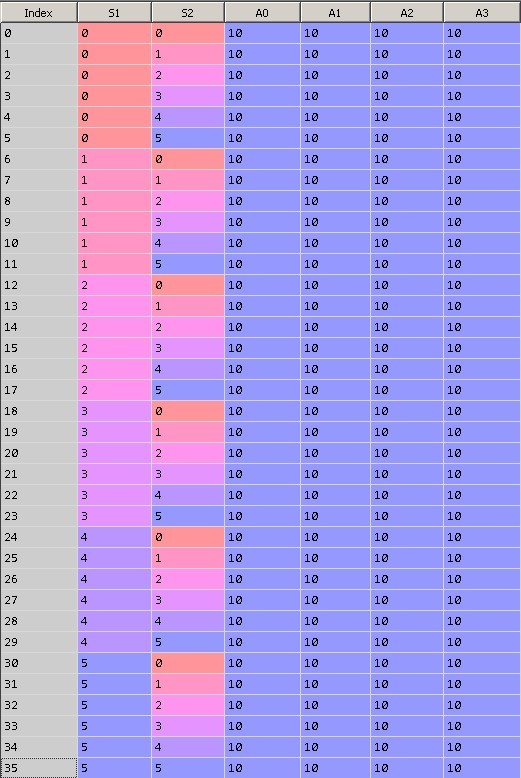
図 9.行列Qの初期化
モデルをトレーニングした後(〜15000回の反復)、行列Qは図10に示す形式になります。

図 10.学習の15000回の反復後の行列Q
重みが10のアクションはシステムで実行できないため、重みの値は変更されていないことに注意してください。 たとえば、S1 = S2 = 0の極端な位置では、アクション1と3を実行できません。これは物理環境の制限であるためです。 これらの境界アクションはモデルでは禁止されているため、アルゴリズムは10kを使用しません。
アルゴリズムの結果を考えます:
...
反復:14991、だった:S1 = 0 S2 = 0、アクション= 0、今:S1 = 1 S2 = 0、賞品:0
反復:14992、だった:S1 = 1 S2 = 0、アクション= 2、今:S1 = 1 S2 = 1、賞金:0
反復:14993、だった:S1 = 1 S2 = 1、アクション= 1、今:S1 = 0 S2 = 1、賞金:0
反復:14994、だった:S1 = 0 S2 = 1、アクション= 3、今:S1 = 0 S2 = 0、賞金:1
反復:14995、だった:S1 = 0 S2 = 0、アクション= 0、現在:S1 = 1 S2 = 0、賞品:0
反復:14996、だった:S1 = 1 S2 = 0、アクション= 2、今:S1 = 1 S2 = 1、賞金:0
反復:14997、だった:S1 = 1 S2 = 1、アクション= 1、今:S1 = 0 S2 = 1、賞金:0
反復:14998、だった:S1 = 0 S2 = 1、アクション= 3、今:S1 = 0 S2 = 0、賞金:1
反復:14999、だった:S1 = 0 S2 = 0、アクション= 0、現在:S1 = 1 S2 = 0、賞品:0
さらに詳しく考えてみましょう。
繰り返し14991を現在の状態とします。
1.システムの現在の状態S1 = S2 = 0、この状態はインデックス0の行に対応します。最高値は0.617(上記の10の値を無視)、アクション= 0に対応します。したがって、行列Qによると、システムの状態はS1 = S2 = 0アクション0を実行します。アクション0は、サーボドライブS1の回転角度の値を増やします(S1 = 1)。
2.次の状態S1 = 1、S2 = 0はインデックス6の行に対応します。重みの最大値はアクション= 2に対応します。アクション2を実行-S2を増やします(S2 = 1)。
3.次の状態S1 = 1、S2 = 1はインデックス7の行に対応します。最大重量値はアクション= 1に対応します。アクション1を実行-S1を減らします(S1 = 0)。
4.次の状態S1 = 0、S2 = 1はインデックス1の行に対応します。最大重量値はアクション= 3に対応します。アクション3を実行します-S2を減らします(S2 = 0)。
5.その結果、彼らは状態S1 = S2 = 0に戻り、1ポイントの報酬を獲得しました。
図11は、最適なアクションを選択する原理を示しています。

図 11.a. マトリックスQ

図 11.b. マトリックスQ
学習プロセスをより詳細に検討してください。
Q学習アルゴリズム
minus = 0; plus = 0; initializeQ(); for t in range(1,15000): epsilon = math.exp(-float(t)/explorationConst); s01 = s1; s02 = s2 current_action = getAction(); setSPrime(current_action); setPhysicalState(current_action); r = getDeltaDistanceRolled(); lookAheadValue = getLookAhead(); sample = r + gamma*lookAheadValue; if t > 14900: print 'Time: %(0)d, was: %(1)d %(2)d, action: %(3)d, now: %(4)d %(5)d, prize: %(6)d ' % \ {"0": t, "1": s01, "2": s02, "3": current_action, "4": s1, "5": s2, "6": r} Q.iloc[s, current_action] = Q.iloc[s, current_action] + alpha*(sample - Q.iloc[s, current_action] ) ; s = sPrime; if deltaDistance == 1: plus += 1; if deltaDistance == -1: minus += 1; print( minus, plus )
GitHubの完全なコード。
膝の初期位置を最高位置に設定します。
s1=s2=5.
初期値を入力して、行列Qを初期化します。
initializeQ();
イプシロンパラメーターを計算します。 これは、計算におけるアルゴリズムの「ランダム性」の重みです。 トレーニングの反復回数が多いほど、選択されるアクションのランダム値は少なくなります。
epsilon = math.exp(-float(t)/explorationConst)
最初の反復の場合:
epsilon = 0.996672
現在の状態を保存します。
s01 = s1; s02 = s2
アクションの「最適な」値を取得します。
current_action = getAction();
関数をさらに詳しく考えてみましょう。
getAction()関数は、システムの現在の状態での最大重量に対応するアクションの値を返します。 Qマトリックス内のシステムの現在の状態が取得され、最大重量に対応するアクションが選択されます。 この関数は、ランダムアクション選択メカニズムを実装することに注意してください。 反復回数が増えると、アクションのランダムな選択は減少します。 これは、アルゴリズムが最初に見つかったオプションに焦点を合わせず、別のパスに進むことができるようにするためです。
矢印の初期の初期位置では、2つのアクション1と3のみが可能で、アルゴリズムはアクション1を選択しました。
次に、システムの次の状態のQ行列の行番号を決定します。システムは、前のステップで受け取ったアクションの後にこの状態に入ります。
setSPrime(current_action);
実際の物理的環境では、アクションを実行した後、動きがあれば報酬が得られますが、トロリーの動きはモデル化されているため、アクションに対する物理的媒体の反応をエミュレートする補助機能を導入する必要があります。 (setPhysicalStateおよびgetDeltaDistanceRolled())
次の機能を実行します。
-選択したアクションに対する媒体の反応をシミュレートします。 サーボの位置を変更し、カートを移動します。setPhysicalState(current_action);
-報酬-トロリーが移動した距離を計算します。r = getDeltaDistanceRolled();
アクションを完了した後、システムの対応する状態のマトリックスQでこのアクションの係数を更新する必要があります。 アクションが正の報酬につながった場合、アルゴリズムの係数は負の報酬よりも低い値で減少するはずです。
ここで最も興味深いのは、現在のステップの重みを計算するために未来を調べることです。
現在の状態で実行する必要がある最適なアクションを決定するとき、マトリックスQで最大の重みを選択します。切り替えたシステムの新しい状態がわかっているため、この状態のテーブルQから最大の重み値を見つけることができます。
lookAheadValue = getLookAhead();
最初は10です。そして、まだ完了していないアクションの重み値を使用して、現在の重みを計算します。
sample = r + gamma*lookAheadValue; sample = 7.5 Q.iloc[s, current_action] = Q.iloc[s, current_action] + alpha*(sample - Q.iloc[s, current_action] ) ; Q.iloc[s, current_action] = 9.75
つまり 次のステップの重み値を使用して、現在のステップの重みを計算しました。 次のステップの重みが大きければ大きいほど、(式に従って)現在の重みを小さくすることはできず、次回は現在のステップが望ましいことになります。
この単純なトリックは、アルゴリズムの良好な収束結果を提供します。
アルゴリズムのスケーリング
このアルゴリズムは、システムのより多くの自由度(s_features)、および自由度(s_states)が取るより多くの値に拡張できますが、小さな制限内です。 十分に速く、QマトリックスはすべてのRAMを占有します。 以下は、状態とモデルの重みのサマリーマトリックスを作成するためのコードの例です。 「矢印」の数s_features = 5および矢印s_statesの異なる位置の数= 10で、行列Qは次元(100000、9)を持ちます。
システムの自由度の増加
import numpy as np s_features = 5 s_states = 10 numActions = 4 data = np.empty((s_states**s_features, s_features + numActions), dtype='int') for h in range(0, s_features): k = 0 N = s_states**(s_features-1-1*h) for q in range(0, s_states**h): for i in range(0, s_states): for j in range(0, N): data[k, h] = ik += 1 for i in range(s_states**s_features): for j in range(numActions): data[i,j+s_features] = 10.0; data.shape # (100000L, 9L)
おわりに
この単純な方法は、機械学習の「奇跡」を示します。モデルは、環境について何も知らずに、アクションに対する報酬が最大であり、アクションに対して即座に報酬が与えられるのではなく、アクションのシーケンスに対して最適な状態を学習および発見します。
ご清聴ありがとうございました!