私はいつも友人に、そのエレガントな抽象化を持つ数学にはその魔法の力があり、その可能性はまだ完全には明らかにされていないと言っていました。 今日は、マンデルブロ集合の助けを借りてPiの数を概算する方法についてお話したいと思います。
多数についてのいくつかの言葉
実際、マンデルブロ集合（以下、集合M ）について説明するHabréの記事は、その特性、歴史、驚くべき美しさを考慮し、カラフルな写真で裏付けています。 私はその定義やその他の詳細にこだわるつもりはありませんが、ポイントに直行します。 しかし、それがこの記事の中心的な主題であるという事実のために、私はまだあなたの記憶をリフレッシュします。
集合Mは、関数が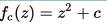 
反復するとき 
限られた。 とても簡単です。
実際には、次の定理を適用します：反復中の関数（上記）が2を超える場合、100％無制限です。 したがって、セットは次のように定義できます。
視覚化のトピックについては触れません。今日は掘り下げません。
パイ番号？
本当に、このように？
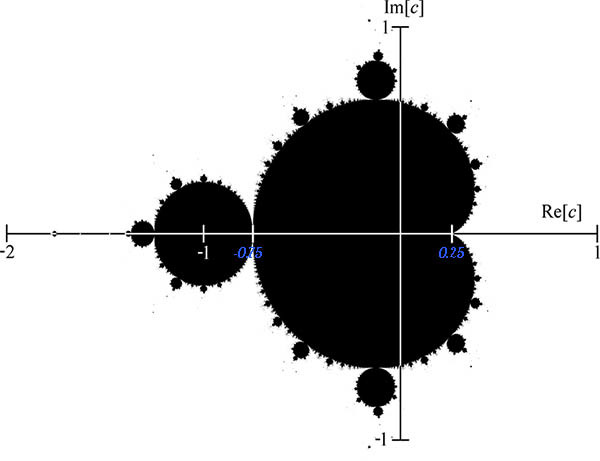
集合c = -0.75 + i x（ここでx∈of）の「2つの部分の接触の座標」を取ります。 それが集合Mに属していることを確認しましょう：関数を繰り返し始めます ゼロからn回、取得した値が2を超えるかどうかを確認します。yesの場合、関数は発散し、 cの値は指定されたnのセットに属しません。 そうでなければ、それは属します。
| x | c | n（関数が消費されるまでの反復回数） |
|---|---|---|
| 0.1 | -0.75 + 0.1i | 33 |
| 0.01 | -0.75 + 0.01i | 315 |
| 0.001 | -0.75 + 0.001i | 3143 |
| 0.0001 | -0.75 + 0.0001i | 31417 |
| 0.00001 | -0.75 + 0.00001i | 314160 |
まさに。 適切な場所にコンマを置くと、数字は数字Piに似ています。
おそらく偶然
複雑な部分を気にせず、数値c = 0.25を取ります。 これは、無限に多数の反復を持つセットに属します。 したがって、この点を右に「アプローチ」します。c= 0.26を取り、チェックします。 c = 0.2501、確認など
| c | n（関数が消費されるまでの反復回数） |
|---|---|
| 0.26 | 30 |
| 0.2501 | 312 |
| 0.25001 | 991 |
| 0.250001 | 3140 |
| 0.2500001 | 9933 |
| 0.25000001 | 31414 |
シーケンスは2つの値の間で変動しますが、Pi番号のエコー（正しい場所にコンマを置く）は消えていません。
ちょっとした歴史
数学者のブノワ・マンデルブロにちなんで名付けられた集合M自体はごく最近の発見です。 ブノワはTEDxで 、彼についても話しました。
1991年、デイブボールはc = -0.75付近の「セットの2つの部分の接触」 Mが「無限に微妙」であるかどうかを研究しました。 彼の研究の過程で、彼は私たちが話していることを発見しました。
それでも、おそらく偶然
何が起こっているのかを理解してみましょう。Pi番号を本当に取得しますか、それとも他の超越的な番号ですか。
このすべてをc = 0.25のポイントで行います（複雑な部品がないため、簡単です）。
再帰関数を考えます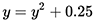 
。 ゼロから反復する場合、非常にゆっくりと値0.5になる傾向があることに注意してください。
この値で「スタック」するのを防ぐために、この関数をε単位上に移動します（ εは無限大であり、ゼロに等しくありません）。 その後、彼女は形を取ります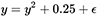 
。
この関数はゆっくりと0.5の値になる傾向があり、渡された後、すぐに無限に逃げます。
さらに掘り下げます。
x = y + 0.5とします。 私たちの仕事はゼロを見つけることです。
元の関数で置換を行うと、次のようになります。 
εを小さな値として、ゼロから関数を測定します。
| y |
|---|
| 0.001（=ε） |
| 0.002001 |
| 0.0030050040010000004 |
| 0.004014034050046026 |
| 0.005030146519400955 |
| 0.006055448893407596 |
| 0.007092117354708267 |
| 0.00814241548328122 |
| 0.009208714413183598 |
| 0.010293514834327173 |
ゼロ付近で非常に滑らかにゆっくりと成長することがわかります。 これに基づいて、関数の（n + 1）番目とn番目の値の差がその導関数に近いと仮定する権利があります。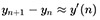 
。
これを考えると、元の関数は次の形式を取ります。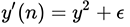 
、1次の最も単純な微分方程式です。 （たとえば、変数の分離方法によって）それを解くと、次のようになります。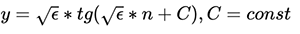 
ゼロの探索という目標を思い出します。 この式は、 εの平方根がゼロに等しい-定義上不可能であるか、接線がゼロに等しい2つの場合にのみゼロに等しくなります。 定数Cを無視する：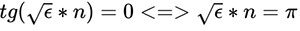 
。 これは、今日見たものを確認します。
| ε | n√ε |
|---|---|
| 0.01 | 3.0 |
| 0.0001 | 3.12 |
| 0.000001 | 3.140 |
| 0.00000001 | 3.1414 |
要因√εが同じコンマを正しい場所に置いていることがわかります。
おわりに
この方法でPi番号を作成することは、おそらく最も非効率的な方法です。3.14160を取得するには、314160回の反復を行う必要があります。 さらに、この方法は、大きな計算エラーのために精度が高くありません。
しかし、フラクタルとその直径の長さに対する円周の比率の2つの一見接続されていない点を接続することができました。