こんにちは、Habr! カラフルな流星雨の後、天文学的な秋に向かってスムーズに進みます。 今年、彼女は私たちに月食、金星と木星の合流 、 そして明るい人工衛星の飛行を前兆としています。 今日の私の話は、このような衛星からの光の反射をシミュレートする方法と、この10月に私たちにとって珍しいことです。

イリジウムの閃光、自分の手での最初の写真-それは間違った方向に向けられ、シャッターが遅く開き、地平線が失敗しました:)
それがすべて始まった方法
春に、Lighthouse衛星に関する投稿がGiktimsに掲載されました。 これは30x10x10 cmの立方体で、その主なタスクは、軌道に入った後、地球に向かって太陽光を反射するミラーフィルムを明らかにすることです。 著者によると、これにより灯台は夜空で最も明るい衛星の1つになるはずです。 海賊行為は、マヤクがロシアで最初の衛星であり、資金がクラウドファンディングによって調達され、非常に成功しているという事実によって追加されています。

( ここから写真 )
Habrは間違いなくケーキです。 コメントでは、開発者も参加したプロジェクトの実行可能性について活発な議論が始まりました。 そして、すべてが衛星の設計に合っていた場合、「空で最も明るい星」に関する記述は非常に驚くべきものでした。 例えば、フィルムミラーはめったに得られないという事実のために。 または、衛星は1秒間に1回転の速度でその軸の周りを回転する必要があるため、地球上の太陽のバニーの速度は非常に大きく、フラッシュは短すぎます。 開発者は、リフレクションの計算に本当に問題があることを認め、これを支援することを提案しました。
Quiensabeによって提案された最初の解析計算。 ( あまり楽観的な結果ではない彼の投稿はGTで公開されましたが、クラウドファンディングへの不注意な参照のため削除されました-しかし、これは別の話です。 )そのような計算は適切な推定を与えましたが、要因の質量-地球の表面の曲率、変化を考慮できませんミラーが回転するときのフラッシュの明るさなど。 正確な数値モデルが必要でした。これは、衛星、観測者、太陽、その他すべての相対位置に応じて、小さな時間ステップで反射の明るさを考慮します。
タスクはそれほど複雑ではないようでした-すべてのジオメトリを注意深く理解し、何も台無しにしないでください。 やる気と何か宇宙のようなものを見つける能力。 もちろん、自分の自転車を書く喜びは貴重です。
( その後、多くの数学があります。結果はここから始まりますが、かなりtl; ここにあります 。 )
アルゴリズム
このモデルの主な目的は、特定の衛星パラメータと地球上の特定の観測者の位置の最大フラッシュ輝度を計算することです。 同時に、数日間のアウトブレイクの予測は途中で行われます。これには、たとえばheavens-above.comがあります。 観測者の上に衛星を1回飛行させることは論理的であり、すでに彼は小さな時間ステップで反射の明るさを計算します。 その後、初期パラメーターを変更することにより、フラッシュの最大可能輝度を計算できます。
したがって、最初のステップ:フラッシュを見るには、衛星が次のことを行う必要があります。a)地平線上を飛行し、b)地球の影にいない。 ステップ2:これらの条件が満たされている場合、フラッシュの明るさの計算を開始できます。 はい、衛星が回転する可能性が非常に高いです-この場合、フラッシュは周期的です。 (サテライトの点滅!)したがって、一般的な場合、3番目の手順が必要です-暗闇の間隔で区切られた個々のフラッシュを検索する。 プログラムのロジックが構築され、3つの関数によって実装されます。
- 最初の関数は、1時間に大きな時間ステップ(1〜5秒)で衛星と観測者の座標を計算し、衛星が地平線の上に見えて影にない瞬間をチェックします。 衛星が地平線の上に表示される場合、関数は、可視の時間間隔を計算し、それらを2番目の関数に渡します。
- 2番目の関数は小さな時間ステップ(0.001-1秒)で機能し、各ステップで観察者が見るフラッシュの明るさを計算します。
- 3番目の機能は、最も非宇宙的です。 彼女は、2番目の関数の結果で個々のフラッシュを見つけ、それらのパラメーターを考慮します:明るさ、持続時間、最大値の通過の瞬間など。
物理モデル
ECI(地球中心慣性)参照系で問題をシミュレートします-その始まりは地球の中心と一致し、Z軸は北極に向けられ、太陽はXZ平面にあります。
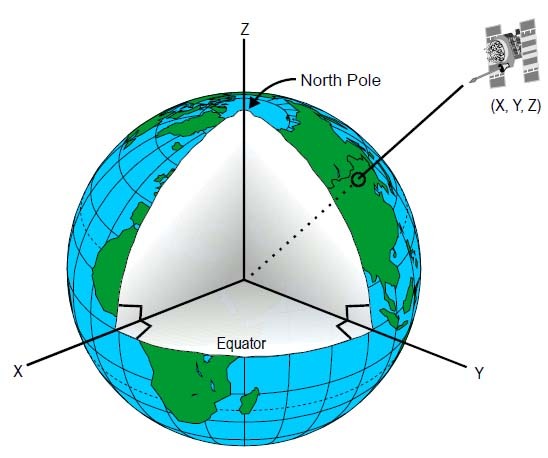
なぜECIなのか 太陽はその中で静止しているため、観測者は地球とともにZ軸を中心に回転し、衛星の軌道は宇宙での位置を変更しません。 これは、衛星と観測者の両方の座標が角度によって簡単にパラメーター化されることを意味します。 詳細はネタバレです。
観測者の座標は、緯度fi obsと現在の経度theta obsによって与えられます。
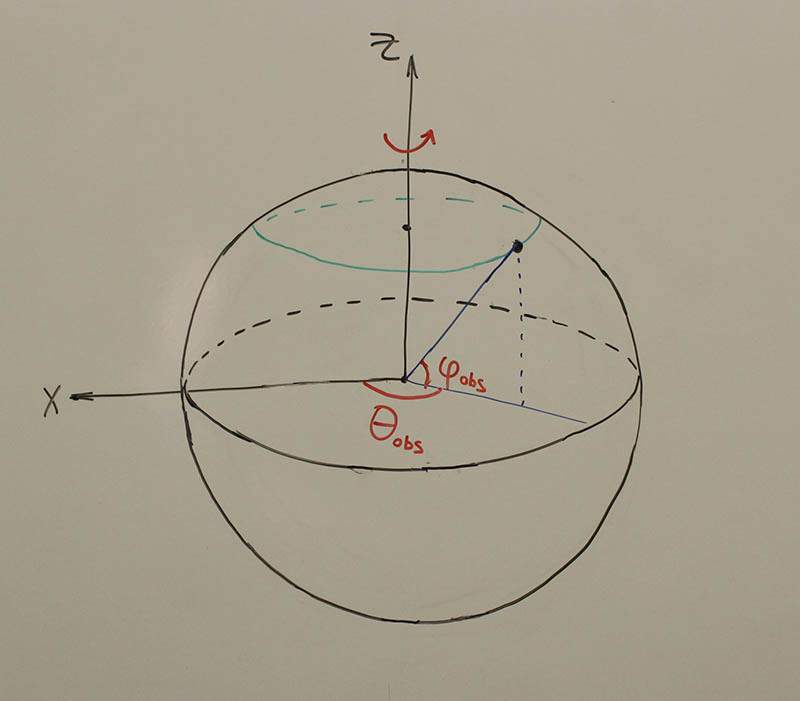
実際、 シータオブスは現地時間です。正午はシータオブス = 0、真夜中- シータオブス = 180に対応します。また、 シータobs0の最初の瞬間の現地時間とその軸の周りの地球の回転速度を知る必要があります。 ECIでの観測者の座標は次のように表されます。

計算を容易にするために、衛星の軌道を円形と見なすことができます。 この場合、半径R orb 、傾斜fi、および上昇ノードtheta ANの経度の3つのパラメーターで指定できます。 上昇ノードは、軌道が北に向かって赤道を横切るポイントです。

重力 心のないあなたは 。 軌道は円形であるため、衛星は一定の角速度で軌道に沿って移動します
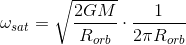
これがすべてわかったので、角度アルファを介して軌道上の衛星の位置を簡単にパラメーター化できます。

ここで、 dir ANとdir Bは、単純な三角法と見なされる、昇順ノードと軌道の最高点への方向です。
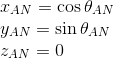

太陽。 ECI参照システムのチップは、太陽が常にXZ平面にあることです。 季節に応じて、位置が変わります。夏が北半球にあるとき、太陽はZ軸の上にあり、冬にはその逆です。 太陽自体の位置には興味がありませんが、太陽に向かう方向に興味があります。 むしろ、彼から、つまり、太陽光線の動きの方向に沿って。 写真では、 k sunと呼ばれています。
座標を見つけましたか? 次に、衛星が地平線の上に見えるかどうかを確認する必要があります。 これは、観測者から衛星までのベクトルの方向dir sat_obsおよび天頂dir obsによって決定されます。それらのスカラー積が正の場合、衛星は私たちの上のどこかにあります。
衛星が地平線の上にある場合は、空の座標を調べる必要があります 。 そのためには、衛星への方向を観測者の平面に投影する必要があります。 オブザーバープレーンは、north dir nordおよびwest dir westへのベクトルによって定義されます。 最初は、天頂への方向と地球の北極d NPを介して配置され、すでにその上にあり、天頂への方向は西へのベクトルが計算されます。

次に、衛星が地球の影にあるかどうかを確認する必要があります (そうでない場合、明らかに、反射はありません)。 次の図から、2つの条件が同時に満たされている場合、衛星が影に隠れていることが簡単にわかります。
- k sunとdir sat (衛星ごとのベクトル)の間の角度は鋭角です。
- d <R
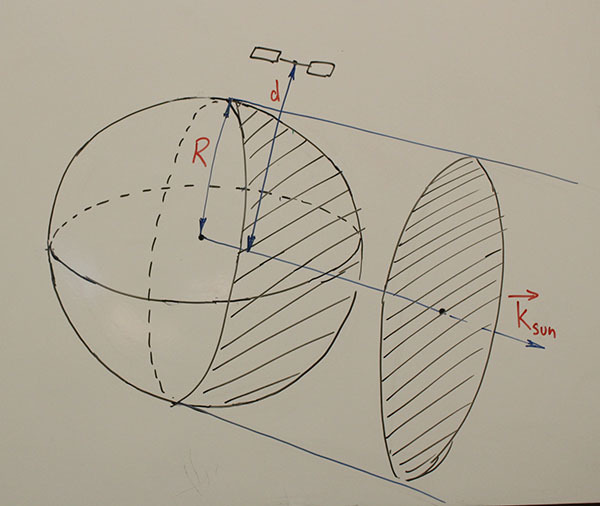
同様に、観測者が影の中にいること、つまり、夜になっていることを確認する必要があります。 日中の天文学には確かに独自の魅力がありますが、日光の下で衛星を見ることは容易ではありません。
最後に、衛星が太陽に照らされており、私たちの上のどこかにある場合、フラッシュの明るさを計算するために残ります。 より正確には、その見かけの大きさは 、他の星と比較して明るさを示しています。 マグニチュードスケールは対数です。次のように定義されます。
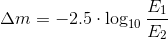
つまり、輝度の100倍の変化は、5単位の大きさの変化に対応します。 また、ここからは、星の光度のスケールが反転していることが明らかです。値が低いほど明るい物体に対応します。 たとえば、北極圏で最も明るい星であるアークトゥルスとベガの光度は+0.0、シリウスは-1.7ですが、金星は-4.6に達します。 目は星を+6等級まで区別しますが、大都市では、露出では+4より明るいものを見ることができません。
大きさを計算するには、明るさ、つまり照明を知る必要があります。つまり、単位面積を通過する光束のパワーです。 W / m 2またはルクスで測定されます。つまり、照明の物理的な意味は、表面がどれだけ明るく照らされるかです。 定義から、照明は面積に依存しないことがわかります。 したがって、肉眼、カメラまたは望遠鏡で観察しても、同じ大きさの測定結果が得られます。
衛星からの反射が作り出す照明を計算する方法は? まず、反射光のパワー(つまり、衛星から反射される1秒あたりの光子数)は、ミラーの面積に太陽によって作られた照明を掛けることによって求められます。 鏡が太陽に対して角度を成すことを忘れてはなりません。 また、ミラーが不均一であり、光を大きな立体角に反射するという事実についても-地球の表面の「バニー」が拡張され、私たちはその中心から遠く離れることができます。 最後に、照明は二次的に衛星までの距離に依存します-衛星が遠ければ遠いほど、観測者に届く光は少なくなります。 照明の最終的な表現は次のようになります。

ここで、 E 軌道は地球の軌道で太陽によって作成された照明、2番目の要因は太陽の光線に対してある角度のミラーの面積、3番目は観測者が見る立体角の割合、4番目は衛星までの距離の2次依存性です。
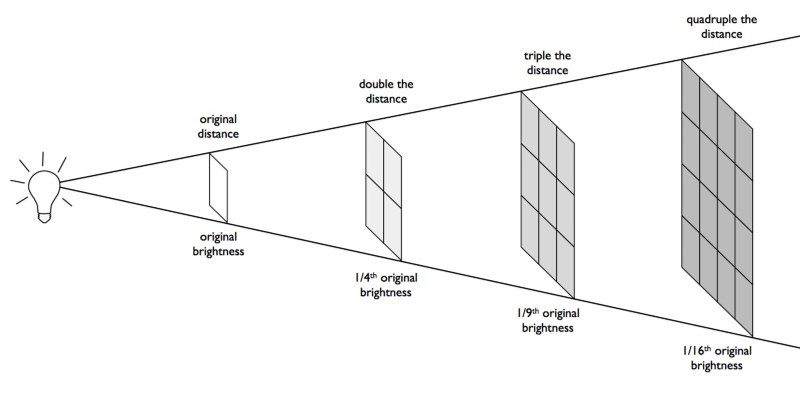
この数値をゼロの大きさ(2.5∙10 -8 W / m 2 )に対応する照明と比較すると、衛星の大きさがわかります。
フラッシュを見るかどうかは、ミラーの位置によって決まります。 法線ベクトルn mirで設定すると便利です。これにより、反射角に等しい入射角に関する古き良きルールに従って、反射光線の方向を簡単に計算できます。

簡単で簡単ですか? まったくない! 実際には、衛星と観測者の特定の位置で反射が観測者に直接当たるように、ミラーの配置方法を検討する方が高速です。 そして、ミラーの現在の位置と比較します。 このアプローチの利点は、タイムステップを変更できることです。 ミラーが最適な位置から遠く離れている間は、ステップを増やすことができます-近い将来、まだフラッシュはありません。 フラッシュが既に開始している場合、最大解像度でフラッシュを計算するには、時間ステップを短縮する必要があります。
最後に、 衛星が回転し、それに伴ってミラーが回転します。 したがって、ミラーn mirの法線を、衛星の回転軸d mirに対して平行と垂直の2つの成分に分解すると便利です。 最初のものは動かずに残り、2番目のものは歳差運動をします-この数学は軌道上の衛星の動きとまったく同じです。
コード
コードはmatlabで記述されています。 上で言ったように、この関数は3つの関数に分かれており、 calc_oneメインスクリプトによって順番に呼び出されます。 メインスクリプトでは、定数、初期条件、およびシミュレーションパラメーターが設定され、次のようにparam構造体を介して関数に転送されます。
% satellite orbit param.incl_sat = 97.75; % inclination, deg (ISS: 51.6, SSO for 600 km: 97.75) param.theta_asc = -7.5; % longitude of the ascending node, deg param.alpha_sat_0 = 0; % angle between AN and the sat in the plane of orbit at t=0, deg param.h_orbit = 600 * 1E3; % orbit height, m
%%%%%%%%%%%%%%%%%% SIMULATION PARAMETERS %%%%%%%%%%%%%%%%%%%%%%%%%% % world param.rad_earth = 6400 * 1E3; % Earth radius, m param.GM = 6.67*1E-11 * 5.972*1E24; % grav. constant times Earth mass, m^3/s^2 param.omega_obs = 1/(60*60*24); % Earth angular velocity, turns/s param.k_sun = [-0.99, 0, 0.16]; % sunlight wavevector (22 Jun: [-0.92,0,-0.4]; 21 Dec: [-0.92,0,0.4], 15 Oct: [-0.99,0,0.16]) param.atmosphere_transmission = 0.7; % atmosphere transmission param.flux_sun = 1367; % Sun irradiant flux on the Earth orbit, W/m^2 param.flux_m0 = 2.5*1E-8; % flux corresponding to the apparent magnitude = 0, W/m^2 param.min_m = 6; % minimal visible apparent magnitude % observer param.phi_obs = 55.75; % latitude, deg (Moscow: 55.75) param.theta_obs_0 = 170; % longitude, deg (noon: 0, midnight: 180) % satellite orbit param.incl_sat = 97.75; % inclination, deg param.theta_asc = -7.5; % longitude of the ascending node, deg param.alpha_sat_0 = 0; % angle between AN and the sat in the plane of orbit at t=0, deg param.h_orbit = 600 * 1E3; % orbit height, m % satellite mirror param.omega_rot = 1; % rotation speed of the satellite, turns/s param.d_rot = [0 0.7 1]; % rotation axis of the satellite param.n_mirror_0 = [1 0 0]; % normal to the mirror at t=0 param.gauss_w = 17.2; % divergence angle of a normal distrubution, deg param.sq_mirror = 3.8; % mirror square, m^2 % simulation parameters param.dt1 = 1; % time step if the satellite is below horizon or in the shadow, s param.dt2 = 1; % same if satellite is above horizon, but reflection is far away param.dt3 = 1 * 1E-2; % same if satellite is above horizon, reflection is close param.dt4 = 5 * 1E-3; % same if reflection is seen param.frame_duration = 0.03; % exposition time of a camera/eye, s
最初の関数 fn_passは、衛星の座標を計算し、水平線上の1つのフライトを検索します。 まず、あらゆる種類の補助値(北極への方向、衛星の回転速度など)を計算します。
% calculate some aux values rad_orbit = rad_earth + h_orbit; % radius of the orbit from the center of Earth r_np = [0 0 rad_earth]; % coordinates of the North pole dir_an = [cosd(theta_asc), sind(theta_asc), 0]; % direction on the acsending node dir_b = [-sind(theta_asc)*cosd(incl_sat),... cosd(theta_asc)*cosd(incl_sat), sind(incl_sat)]; % direction on the highest point of the sat omega_sat = sqrt(2*GM/rad_orbit)/(2*pi*rad_orbit); % satellite angular velocity on the orbit, s^-1 dir_obs_z = sind(phi_obs); % z-coordinate of the observer, does not change
その後、whileサイクルは1秒に等しい一定のステップで時間内に開始します。 サイクルを終了するための条件は、衛星が地平線を超えていることです(または、衛星が地平線上に1回出現せずに2回転しているため、低軌道では非現実的です)。 サイクルでは、観測者と衛星の座標が順番に計算されます。
% coordinates of the observer theta_obs = mod(theta_obs_0 + 360*omega_obs*current_time, 360); dir_obs = [cosd(phi_obs)*cosd(theta_obs), cosd(phi_obs)*sind(theta_obs), dir_obs_z]; r_obs = rad_earth * dir_obs; % coordinates of the satellite theta_sat = mod(alpha_sat_0 + 360*omega_sat*current_time, 360); dir_sat = cosd(theta_sat)*dir_an + sind(theta_sat)*dir_b; r_sat = rad_orbit*dir_sat; % vector from the satellite to the observer r_sat_obs = r_obs-r_sat; dir_sat_obs = fn_norm(r_sat_obs);
衛星が地平線上にあり、空の座標が計算されていることが確認されます。
% CHECK1: check if the satellite is above the horizon if fn_dot(dir_obs, dir_sat_obs) < 0
% basis on the skychart r_obs_np = r_np - r_obs; % vector from the observer to the North pole dist_obs_np = sqrt(sum(r_obs_np.^2)); cos_angle_obs_np = fn_dot(r_obs_np, -dir_obs)/dist_obs_np; dir_nord = r_obs_np + cos_angle_obs_np*dist_obs_np*dir_obs; dir_nord = fn_norm(dir_nord); % vector to the nord dir_west = fn_cross(dir_obs, dir_nord); dir_west = fn_norm(dir_west); % vector to the west % coordinates of the satellite on the sky chart pass_path.alt(pass_step,1) = 90 - acosd(fn_dot(-dir_sat_obs, dir_obs)); map_proj_nord = fn_dot(-dir_sat_obs, dir_nord); map_proj_west = fn_dot(-dir_sat_obs, dir_west); pass_path.azimuth(pass_step,1) = mod(-atan2d(map_proj_west, map_proj_nord), 360);
最後に、衛星が影になっているかどうかを確認します。
% CHECK 2: check that the satellite is not in the shadow cos_angle_sat_ksun = fn_dot(dir_sat,k_sun); dist_sat_ksun = rad_orbit*sqrt(1-cos_angle_sat_ksun^2); % distance from the sat to the central axis of shadow if (dist_sat_ksun > rad_earth) % satellite is not in the shadow
すべてのデータは、関数が返すpass_path構造に格納されます。 しかし、その前に、衛星が地平線の上にあり、太陽に照らされている間のすべての間隔を見つける必要があります-これらは、2番目の機能が機能するために必要です。
% STEP 2: if the pass was above horizon, % select the regions when sat is above horizon and not in shadow pass_path.reflection_intervals = []; if isempty(pass_path.time) == 0 flag_in_shadow = 1; num_regions_not_in_shadow = 0; for counter_step = 1:size(pass_path.time,1) if pass_path.in_shadow(counter_step) == 0 % satellite is not in shadow if flag_in_shadow == 0 % sat is still not in shadow else % sat was in shadow and just went out of it flag_in_shadow = 0; num_regions_not_in_shadow = num_regions_not_in_shadow + 1; pass_path.reflection_intervals(num_regions_not_in_shadow,1) = pass_path.time(counter_step); end else % satellite is in shadow if flag_in_shadow == 0 % sat was not in shadow and just went into it flag_in_shadow = 1; pass_path.reflection_intervals(num_regions_not_in_shadow,2) = pass_path.time(counter_step); else % sat is still in shadow end end end % if at the end sat was still not in shadow, % time of the end of the last interval will be time of the last % point above the horizon if flag_in_shadow == 0 pass_path.reflection_intervals(num_regions_not_in_shadow,2) = pass_path.time(counter_step); end end
間隔はNx2配列のpass_path.reflection_intervalsに格納されます。Nは可視性の間隔の数、2つの数値は可視性の間隔の開始時間と終了時間です。 これで、 pass_path構造がメインスクリプトに戻り、そこから2番目の関数が呼び出されます。
2番目の関数 fn_reflectionは、衛星が地平線上にあり、太陽によって照らされている間隔でのみ機能します。 各ステップ(1秒より短い場合もあります)で、観測者と衛星の座標も計算し、ミラーが最適な位置に近いかどうかを確認します。
% CHECK 3: if angle (d_rot, n_opt) is close to angle (d_rot, n_mir0), proceed % this means that geometry can in principle give a reflection if (angle_drot_nopt > (angle_drot_nmirror-angle_div))... && (angle_drot_nopt < (angle_drot_nmirror+angle_div)) % current orientation of the mirror n_mir = n_mir_parallel... + n_mir_perp0*cosd(360*omega_rot*current_time)... + n_mir_perp1*sind(360*omega_rot*current_time); % angle between current orientation of the mirror and n_opt angle_nmir_nopt = acosd(fn_dot(n_mir, n_opt)); % CHECK 4: if n_mir is close to n_opt, proceed and calculate the reflection if angle_nmir_nopt < angle_div
コードからわかるように、ミラーの位置は、衛星の回転軸に対する方位角( CHECK 3 )と放射角( CHECK 4 )の2つのパラメーターによってチェックされます。 秘Theは、衛星が回転すると放射角が変化することです。 しかし、方位角-いいえ!
したがって、最初は、方位角が最適な位置に近いかどうかを確認するのが理にかなっています。 そうでない場合、近い将来、何も助けになりません。 その場合、放射角を計算し、同時に時間ステップを減らすことができます。
最後に、ミラーが最適な位置に近い場合、ソーラーバニーによって作成された照明を計算できます。 まあ、同時に大きさ
% calculate the angle between the direction on the observer % and direction of the main reflection cos_angle_nmir_ksun = fn_dot(n_mir, -k_sun); k_refl = 2*cos_angle_nmir_ksun*n_mir + k_sun; cos_angle_refl_obs = abs(fn_dot(k_refl, dir_sat_obs)); angle_refl_obs = acosd(cos_angle_refl_obs); % flux at the observer's place refl_fraction = 2/(pi*degtorad(gauss_w)^2) * exp (-2*angle_refl_obs^2/gauss_w^2); % now it is Gaussian int_reflection = flux_sun * sq_mirror * cos_angle_nmir_ksun; flux = max (int_reflection * refl_fraction ... * atmosphere_transmission / distance^2, flux_min); % W/m^2
輝度が低すぎる(調光器+6)場合、結果に+6が書き込まれることがわかります。 これは、何も表示されないことを意味します。 すべての結果はパス構造に書き込まれ、関数はそれを返します。
3番目の関数 fn_flaresは最も単純です。フラッシュ、最大輝度、持続時間、空の位置をカウントします。 それは本当に原始的ですが、長いので、ネタバレの下に置きました。
function pass = fn_flares(pass, param) % this functions counts the flares into the 'pass' structure % summarizes data about their magnitudes, durations, etc. % and saves them in 'pass.flares' field % initialization before the main loop counter_flare = 0; flare_is_now = 0; clear flares flares = struct('time',[],'dist',[],'alt',[],'azimuth',[],'inst_magn',[],'vis_magn',[],'dur',[]); % main loop for step = 1:length(pass.time) if pass.magnitude(step) < param.min_m % flare is present now if flare_is_now == 0 % flare just began flare_is_now = 1; counter_flare = counter_flare + 1; clear current_flare current_flare.time_beg = pass.time(step); % integrate the energy of the flare, [J/m^2] if step < length(pass.time) current_flare.energy = pass.flux(step)*... (pass.time(step+1) - pass.time(step)); else % this was the last data point, nothing to add end % create field 'current_flare.brightest' % with the data about the brightest point of the flare current_flare.brightest.magn = pass.magnitude(step); current_flare.brightest.time = pass.time(step); current_flare.brightest.azimuth = pass.azimuth(step); current_flare.brightest.alt = pass.alt(step); current_flare.brightest.distance = pass.distance(step); else % flare still goes on % increment the energy of the flare if step < length(pass.time) current_flare.energy = current_flare.energy + pass.flux(step)*... (pass.time(step+1) - pass.time(step)); else % this was the last data point, nothing to add end % if here flare is brighter, renew the data about the brightest point if pass.magnitude(step) < current_flare.brightest.magn current_flare.brightest.magn = pass.magnitude(step); current_flare.brightest.time = pass.time(step); current_flare.brightest.azimuth = pass.azimuth(step); current_flare.brightest.alt = pass.alt(step); current_flare.brightest.distance = pass.distance(step); end end else % no flare now if flare_is_now == 0 % still no flare else % flare just ended, sum up the results flare_is_now = 0; current_flare.time_end = pass.time(step-1); current_flare.duration = current_flare.time_end - current_flare.time_beg; if current_flare.duration > param.frame_duration % if the flare is long, we can see it directly current_flare.vis_magn = current_flare.brightest.magn; else % if the flare is short, one should divide its energy % over the exposure time of an eye/camera to get the % apparent magnitude current_flare.vis_magn = ... min(-2.5*log10(current_flare.energy/param.frame_duration/param.flux_m0), param.min_m); end % save the data in the 'flares' structure flares.time(counter_flare,1) = current_flare.brightest.time; flares.dist(counter_flare,1) = current_flare.brightest.distance; flares.azimuth(counter_flare,1) = current_flare.brightest.azimuth; flares.alt(counter_flare,1) = current_flare.brightest.alt; flares.inst_magn(counter_flare,1) = current_flare.brightest.magn; flares.vis_magn(counter_flare,1) = current_flare.vis_magn; flares.dur(counter_flare,1) = current_flare.duration; end end end % return the result flares.num_of_flares = counter_flare; pass.flares = flares; end
1つの問題がここに表示されます。 フラッシュが非常に短い場合、瞬間の輝度が大きくても、目の中の光子の総数は少なくなります。 フラッシュの見かけの明るさは最大値よりもはるかに低くなります。
ショートフラッシュとはどういう意味ですか? 明らかに、カメラの露出時間よりも短いものです。 そして、それを目で見ると? 目の露出として考慮すべきこと、私はメクロンに尋ねた理由がわからなかった 。 彼は多くの興味深いことを話しました-しかし、それは目が一生懸命に働いているという事実に帰着しました、彼の感受性は非常に非線形であるため、質問に対する明確な答えを与えることはできません。 大体ですら。 結果として、多少意味のある数を選択することになりました-私は30ミリ秒を選択しました。これは1秒あたり約30フレームに相当します。
そのため、フラッシュが露光時間よりも短い場合、その持続時間は露光時間に切り上げられ、総光量は変化しませんが、それに応じて輝度は低下します。 たとえば、実際にフラッシュが10ミリ秒続き、この間に3000光子が到着した場合、瞬間的な「明るさ」は300光子/ミリ秒です。 100フォトン/ミリ秒の「明るさ」で30ミリ秒持続したことがわかります-瞬間的なものの3倍です。
最後に、メインの calc_one スクリプトは最初に最初のfn_pass関数を呼び出し、衛星が地平線の上に見えて影がない場合、 fn_reflection関数で反射の明るさを、 fn_flares関数でフラッシュパラメータを考慮します。
% calculate trajectory of the pass pass_path = fn_pass(param); % proceed if the satellite is above the horizon and not always in shadow if isempty(pass_path.reflection_intervals) == 0 % calculate the reflections and magnitudes of flares pass = fn_reflection(param, pass_path.reflection_intervals); pass = fn_flares(pass, param); end
最適化
最初の最適化手法についてはすでに述べましたが、これは可変時間ステップです。 fn_pass関数は大きな増分(1秒)で機能します-衛星が地平線の上に見えるかどうかを確認するには、これで十分です。 ただし、 fn_reflection関数には 3つのタイムステップがあります。フラッシュプロファイルの計算には最小(最大1ミリ秒)が必要で、他の2つはフラッシュが見えないがすぐに表示される場合があります。 これらは、パラメーターを使用して構造体で定義されます。
param.dt1 = 1; % time step if the satellite is below horizon or in the shadow, s param.dt2 = 1; % same if satellite is above horizon, but reflection is far away param.dt3 = 1 * 1E-2; % same if satellite is above horizon, reflection is close param.dt4 = 5 * 1E-3; % same if reflection is seen
2番目のポイントは、組み込みのMatlab関数に関連付けられています。 それらは普遍的であると考えられていました-例えば、同じ余弦は実数と複素数の両方から、単一と配列の一部の両方として考えることができます。 当然、この汎用性のために、入力パラメーターを確認する必要があります。 スカラー積などの単純な関数の場合、このテストは実際の数学よりも時間がかかる場合があります。
function c = dot(a,b,dim) if isinteger(a) || isinteger(b) error(message('MATLAB:dot:integerClass')); end % Special case: A and B are vectors and dim not supplied if ismatrix(a) && ismatrix(b) && nargin<3 if min(size(a))==1, a = a(:); end if min(size(b))==1, b = b(:); end end; % Check dimensions if any(size(a)~=size(b)), error(message('MATLAB:dot:InputSizeMismatch')); end if nargin==2, c = sum(conj(a).*b); else c = sum(conj(a).*b,dim); end
このコードでは、ベクトルとスカラー積だけでなく、ベクトルの正規化も最もよく呼び出されます。 したがって、チェックなしで関数を作成するのは理にかなっています。すべてのベクトルは明らかに3次元であり、コンポーネントは実在するためです。
function c = fn_dot(a, b) c = a(1)*b(1) + a(2)*b(2) + a(3)*b(3); end
その後、計算速度は2倍になりました。
コードはgithubにあります。 フレアの計算はイリジウムで確認され、意味のある結果が得られました-フラッシュの明るさは約-9等級でした。
灯台
マヤック衛星は、今年10月に高さ600 kmの円形軌道で打ち上げられる予定です。 ロシア中部では、現地時間の午後10時から午前2時の間に最もよく見られます。 灯台フィルムミラーは、イリジウムアンテナよりもはるかに悪い光を反射しますが、エリアではそれらを上回ります。
| パラメータ | 価値 |
|---|---|
| 軌道の高さ | 400〜600 km |
| 軌道傾斜 | 97.7° |
| 上流への方向 | -7.5° |
| ミラーエリア | 3.8 m 2 |
| 反射の発散(1σ) | 17.2° |
| 回転速度 | 不明(予想される0.5-1 rpm) |
| 回転軸の向き | 不明 |
軌道に入った後、衛星はミラーを開き、毎秒約1回転の速度で回転します。 問題は、スピン軸の方向が原理的に不明であるということです -衛星には方位システムやテレメトリーがありません。 これに加えて、キューブセートをキャリアから分離するときにねじれが追加されます。 たとえば、ISSから打ち上げられた2つのカブサットです。 起動直後に、すでにさまざまな方法で回転していることがわかります。

calc_oneスクリプトでミラーの回転軸と方向のランダムな方向を設定し、観測者が衛星の通過を見るかどうかを確認するために残ります。
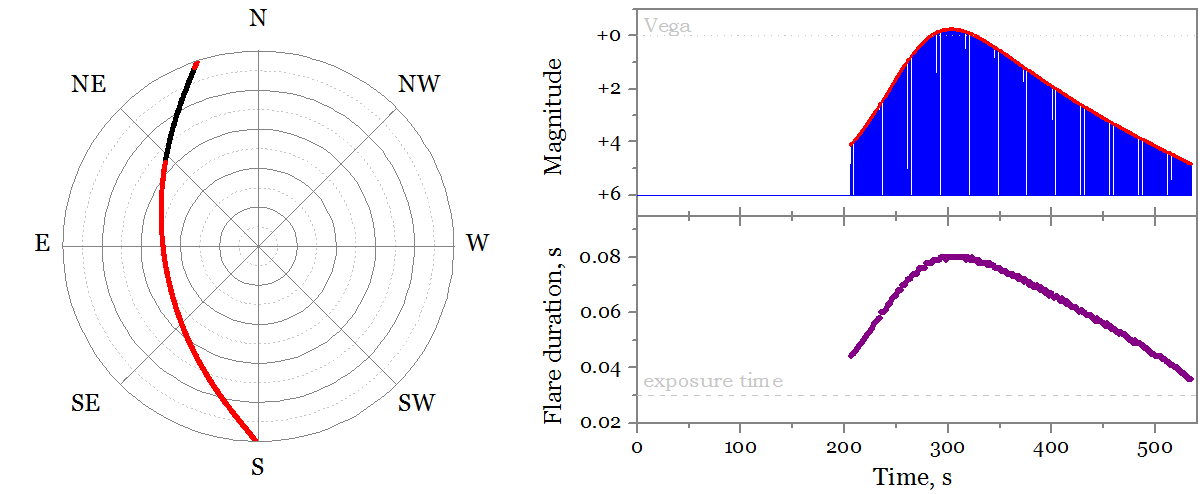
うわー、何かが見える! 左はモスクワの空の衛星飛行経路で、夕方11時頃です。 赤い点は衛星の目に見える閃光であり、黒い線は地球の影にある衛星であり、見えません。 右側のグラフは、時間に応じたフラッシュの明るさ(上)とその持続時間(下)です。 フラッシュは明るいが、短いことがわかります。 そして、豊富なポイントから判断すると、実際には多くのポイントがあります(スクリプトは330を数えました)。
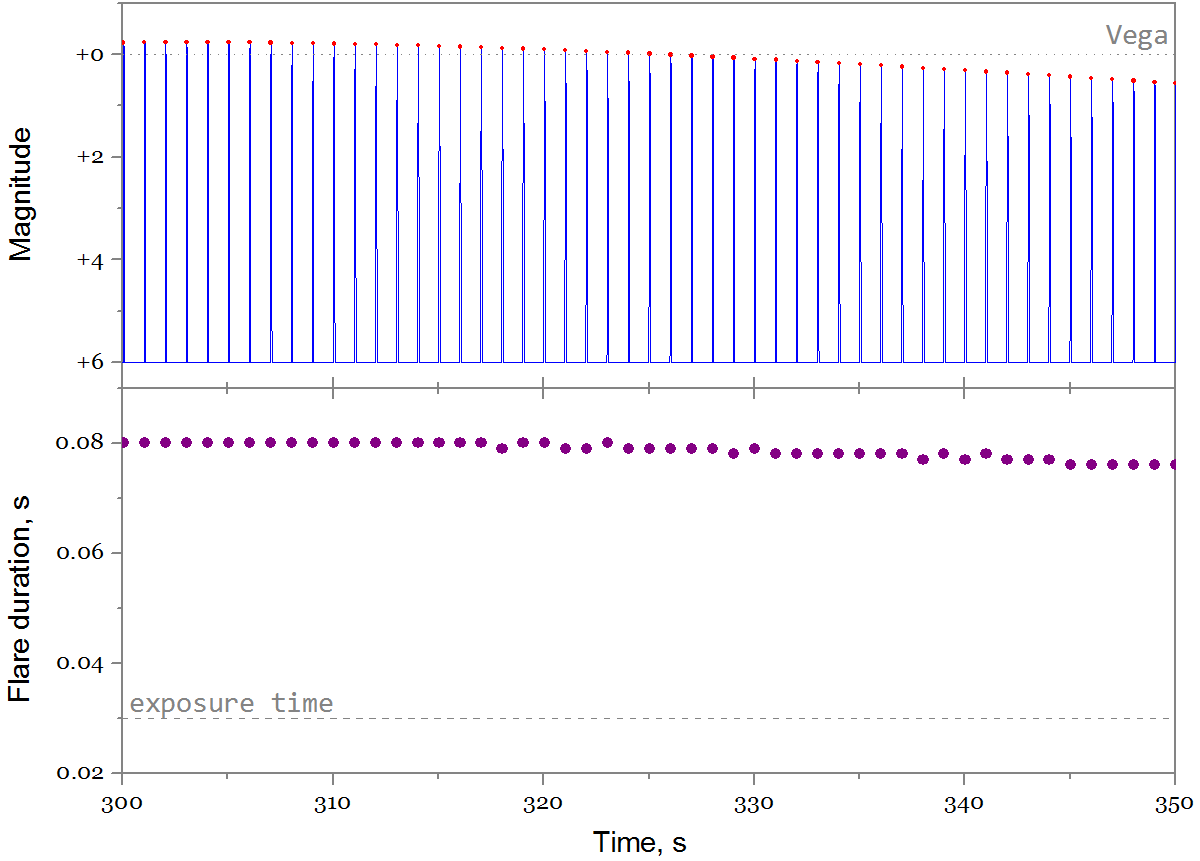
毎秒フラッシュで! キャプテンエビデンスは、これが衛星が1 r / sの速度で渦巻くためのものであるべきだと示唆しています。 そして、単一のフラッシュのプロファイルは次のようになります。

フラッシュは非常に短く、背景より暗くなると+6の大きさで途切れます。
私たちを心配している主な質問は、フラッシュを見るのが最適なのはいつですか? これを行うには、オブザーバーのさまざまな位置(=さまざまな現地時間)に対してスクリプトを実行できます。 衛星の向きがわからないという事実はどうですか? 毎回、ミラーと回転軸のいくつかのランダムな方向の計算を実行し、最も明るいフラッシュを選択できます。 コードは次のように変更されます。
line_theta_obs_0 = 134:2:236; % values of theta_obs_0 to be simulated number_of_iterations = 50; % number of different mirror orientations for one data point for counter_theta_obs_0 = 1:size(line_theta_obs_0,2) param.theta_obs_0 = line_theta_obs_0(counter_theta_obs_0); % calculate trajectory of the pass pass_path = fn_pass(param);
衛星が地平線上を飛行する場合、
% loop over different random orientations of the mirror for counter_mirror = 1:number_of_iterations % create randomly oriented mirror and rotation axis param.d_rot = [rand, rand, rand]; param.n_mirror_0 = [rand, rand, rand]; % calculate the reflections and magnitudes of flares pass = fn_reflection(param, pass_path.reflection_intervals); pass = fn_flares(pass, param); end
観測者の50の位置と衛星の50のランダムな向きで起動し、真夜中を待ちます(そう、シミュレーションには多くの時間がかかります)。結果が得られます。

最も明るいフラッシュは真夜中に発生します 。これは、観測に非常に便利な時間です。 夜のフラッシュも明るくなる場合があります。 残念ながら、シリウスと惑星よりも明るく輝くことはできませんが、状況が成功すれば衛星はかなりよく見えます。 フラッシュの明るさは、衛星が天頂から遠ざかるにつれて低下することがわかります(下の青いグラフ)。これは、水平線の近くを飛行するときの衛星までの距離の増加に関連しています。 同時に、フラッシュの持続時間(平均的な紫色のグラフ)は実質的に変化しません。
明るい閃光が見える確率はどれくらいですか? 問題の唯一のランダムな要素は、軌道上の衛星の向きです。 衛星の向きに基づくサイクルでは、各反復のフラッシュの明るさを保存してから、ヒストグラムを作成する価値がありました。 ( くそー、すぐにそれについて考えなければなりませんでした! )必要なコードを追加し、100の衛星方向のスクリプトを実行します。 翌朝、結果が得られます。

ここでは、異なる明るさのフラッシュが異なる色で表示されます。 チャートの列-特定の現地時間。 あらゆる種類の明るさのフラッシュの確率は100%です。 結果は期待外れであることがわかります。
- Vega(大きさ+0)よりも明るいフラッシュは、11:15から00:15までの1時間以内に見られます。 この確率は約10%です。
- おおぐま座とカシオペア座の星(明るい+2)が2時間より少し長く見える(午後10時から12時半まで)よりも明るく見える場合、それらを見る確率は約20%です。
- 50%を超える確率で、アウトブレイクはまったくありません 。
さて、朗報:衛星には3つのミラーがあります。 これは、確率が3倍になることを意味するものではありません(150%の無意味な確率が得られるという理由だけで)。 しかし、ミラーの配置が成功すれば、確率の2倍の増加は非常に現実的であり、非常に優れています。 運がよければ、2つのミラーからのフラッシュを順番に観察することができます。 はい、これは明るさにまったく影響しません-真夜中頃の「最終時間」でのみベガより明るいものを見ることができます。
他のものを数えましょう。 たとえば、衛星の回転速度に応じてフラッシュの明るさがどのように変化するか 。
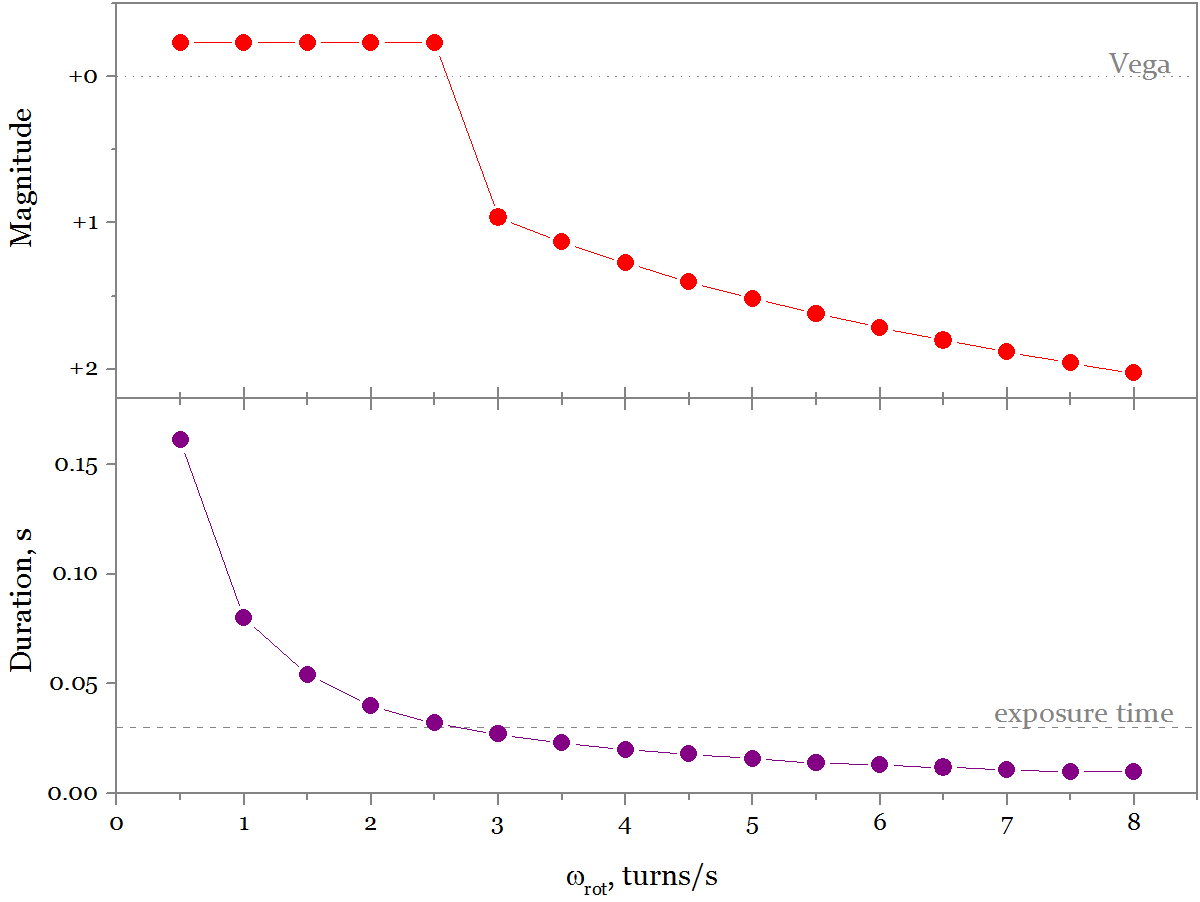
衛星の回転が速すぎると、フラッシュが短くなりすぎます(下のグラフ)。 その後、カメラ/目は、露出時間を可能な限り最小(1フレームまたは0.03秒)に丸めます。 フラッシュの輝度は何度も低下します。 私たちの場合、これは3 r / sのスピンで発生します。
そして、回転速度が小さすぎる場合はどうなりますか? また、最大0.01 r / sまで大丈夫です。 しかし、フラッシュの下はめったに行きません-最初のフラッシュが天頂よりずっと前に終了し、2番目のフラッシュが強く開始することがあります。 私の知る限り、マヤックは0.1-1 r / sの速度で回転しますが、これは上限と下限から遠いです-つまり、ねじれがあると頻繁に明るい閃光が見えるはずです。
さて、今悲しいことについて。 マヤックセンチュリーは非常に短い - 住んでいる -その巨大なミラーは、600 kmの高度でも残留大気について減速します。 月の間に、衛星は400 kmに減少し、そこでブレーキはさらに強くなり、その後数日以内に大気の密な層に入ります。 , , 0.6 :
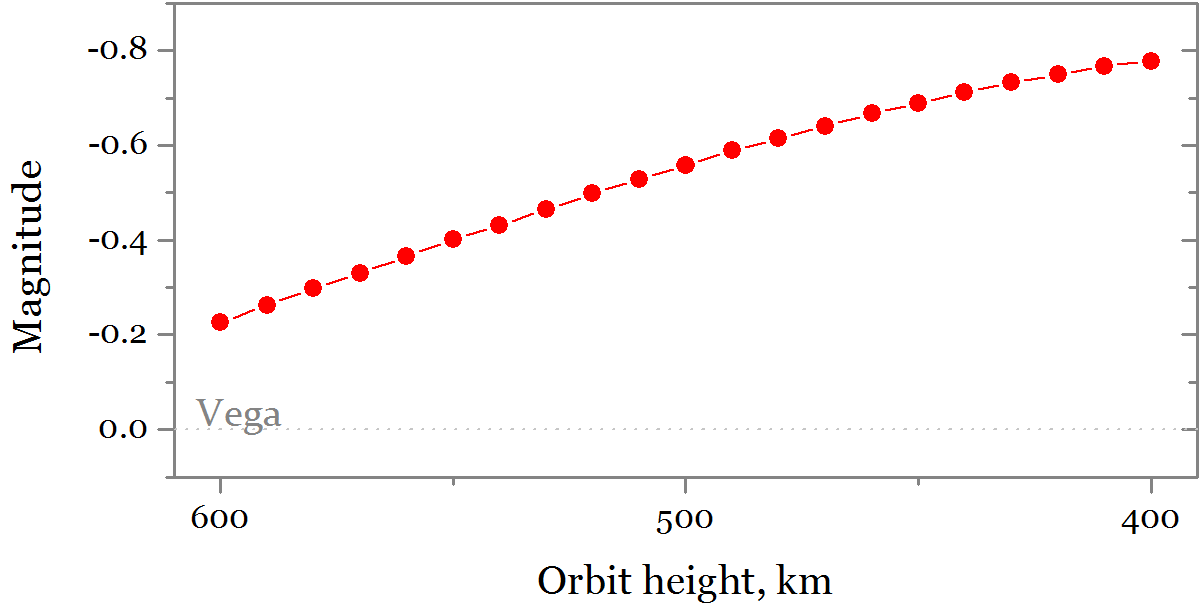
- . " " — , , .
- ( , , - ) — 20 %.
- — "" .
, – GUI, , , CUDA . , . .
, Quiensabe . – , , !