コンピューティング翻訳の大原則
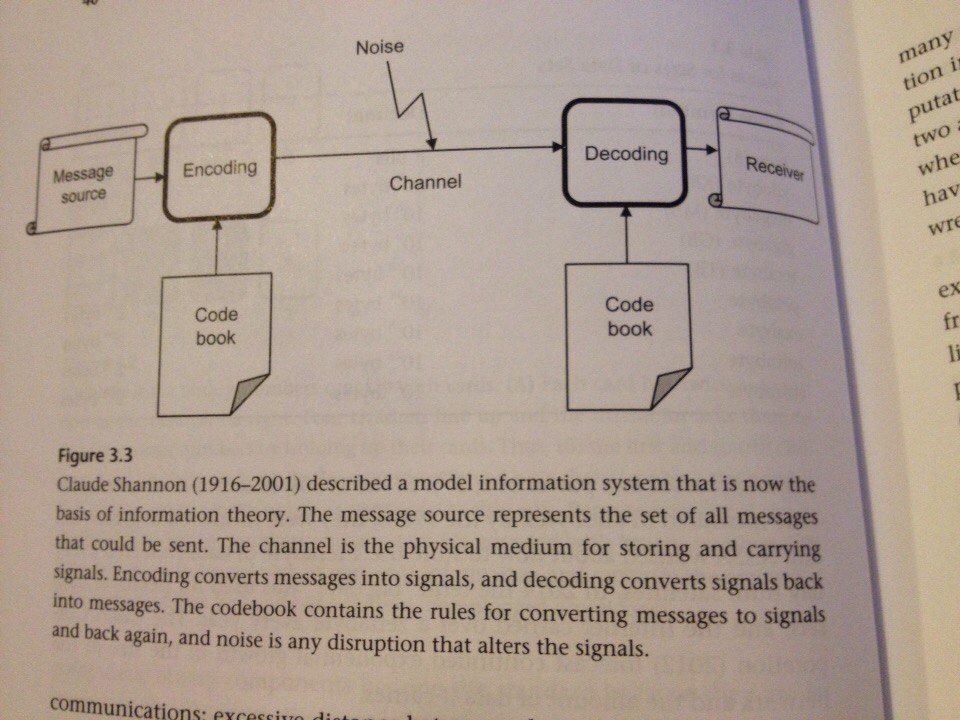
1948年、シャノンは「コミュニケーションの理論」でコミュニケーションの数学的モデルを提案しました。 その意味は次のとおりです。
ソースがあり、レシーバーがあります。 ソースはメッセージを送信し、受信者は受け入れます。 両方の参加者は、メッセージのエンコードとデコードに同じ辞書を使用します。
Shannonモデルは、メッセージをエンコード、デコード、送信、保存、および受信するすべてのシステムに適用できます。 このように、自然は物理法則(メッセージ)の源泉であり、これらの法則を発見するプロセスはコミュニケーションチャンネルであると考えることができます(Dretske 1981)。
ノイズはこのモデルの別のコンポーネントです。 ノイズは、受信者がメッセージを誤って解釈する原因となります。 視界不良(霧と薄明)により、船舶間のセマフォ通信が中断されます。 稲妻の閃光は、AM電波の送信を中断します。 CDに傷があると、CDが読み取れなくなる可能性があります。 バックグラウンドノイズが多いと、音声が判読できなくなります。
通信システムでの暗号化は、秘密メッセージの暗号化と同じではないことに注意してください。 暗号化は、特別なキーの存在を前提としています。このキーを持つキーのみがソーステキストを取得できます。
彼のモデルでは、シャノンは「エンコード辞書」としてビットを選択しました。 彼は、どんなメッセージもビットのセットとして表現できると主張した。 文字通りデジタル化されると、情報は数字に変わり、ゼロと1のセットになります。
簡単な例を使用して、メッセージをデジタル化する方法とノイズとは何かを見るのは興味深いことです。
ソースは、A、B、C、Dの4文字で構成されるメッセージのみを送信します。これらの文字を示すには、2ビットコードを使用します。
A:11
B:10
C:01
D:00
たとえば、ソースは「CAB」と言いたいです。 このメッセージは、コード「011110」に対応しています。 ソースはこのビットのセットをチャネルに送信し、レシーバはそれらを受信して逆のプロセスを開始します。コードをビットのペアに分割し、辞書と照合します。
疑問が生じます:これらの文字をエンコードするには2ビットで十分ですか? 当然、この目的のために必要なビットは少ないほど良いです。メッセージの占有スペースが少なく、より速く送信されます。 ただし、短いコードは台無しになりやすく、ノイズによってわずかな歪みが発生します。
たとえば、文字Aの最初のビットが何らかの理由で失われた場合、010110を取得します。これはCCBに対応し、これによりメッセージの意味が完全に変わります。 になる方法
各文字に追加のビット(パリティビット)を追加します。
A:110
B:101
C:011
D:000
ここで、Aの最初のビットが失われた場合、010が得られます。辞書にはそのようなトリプルがないため、受信者はこれがエラーであることを容易に理解できます。 ただし、元のメッセージを復元することはできません。
いくつかの余分なビットを追加すると、受信者はエラーの場所を見つけるだけでなく、ソースコードを復元するのに役立ちます。
A:11111
B:10010
C:01001
D:00100
各コードは、少なくとも3ビットだけ互いに異なります。 スポイルされたビットは、真のビットと1ビットずつ異なるセットを示していますが、辞書の他のすべてのビットとは2ビット以上異なります。 したがって、受信者は破損したメッセージを簡単に「修正」できます。
通信エンジニアのリチャードハミングは、ビットセット間の十分な「距離」を決定するルールを最初に策定しました。 ハミングによれば、距離はビットのセットであり、それによってビットのセットは互いに異なります。 現在、この量はハミング距離と呼ばれています。
ハミングは、k個のエラーを修正するために、ハミング距離が2 ^ k-1で十分であることを認識しました。元のメッセージを受信します(エラーの修正を考慮に入れます)。 ハミングコードは、プロセッサからコンピューターのメモリにメッセージを送信するときに広く使用されます。
ノイズがランダムに分布している場合、ハミングコードはうまく機能します。 ただし、一部の信号では、ノイズが定期的に、または比較的長時間発生します。 別のタイプのコードがこれをうまくやっています-リードソロモンコード。 数学の観点から見ると、それらはより巧妙ですが、どちらもコンピューターの集積回路で簡単に実行できます。