このプロジェクトの歴史は2014年に始まります。2014年、ロシアのロボットシステム学科の一流の技術大学で4年生を過ごしました。 この時点で、私はすでに卒業証書のトピックについて考え始めていて、私にとって興味深いプロジェクトを探していましたが、同時にいくつかの斬新さがありました。 そしてある日、Rezero 投票のビデオを見た後、私と私の友人は成功を繰り返したいと思っていました。 誰がそれをもたらしたのか気にします-私は猫を求めます。

はじめに
初めに、シャロボットのメリットについてお話したいと思います。 表面との単一の接触点のおかげで、球形ロボットはすべての方向に等しく容易に移動し、従来の車輪付きロボットと比較して非常に可動性が高く、機動性があります。 球形ロボットの機動性は、車輪によって課される機械的な制限(たとえば、横に移動できないこと)とは対照的に、その動力学によってのみ制限されます。
次の重要な利点は、ロボットが背が高くなる可能性があり、高ければ高いほど安定することです。 なぜより持続可能なのか? これは、逆振り子のダイナミクスの方程式から見ることができます。 垂直平衡からの逸脱の加速は、重心までの距離に反比例します。 より高い逆振り子はよりゆっくりと落下します。 これにより、制御システムの反応速度の要件は緩和されますが、場合によっては、ドライブが発生する瞬間が増加します。
別の利点は、離陸中に船の甲板や飛行機の床など、傾斜した動く表面に乗ることができることです。 はい、あなたは認めなければなりません、それは普通の車輪付きロボットよりもはるかに美しく動きます。
球形バルーンの主な欠点の1つは、垂直方向の平衡位置を失う可能性です。 しかし、個人的には、これは完全に解決可能なエンジニアリングタスクだと思います。 ロボットエンジニアのAidoとMobiは、次のようにそれを解決しました。一定の逸脱角度を超えると、ロボットの安定性が失われないように「脚」が延長されます。
私のストーリーは次の部分で構成されています。
-数学モデル
-制御アルゴリズムの開発
-建設
-ハードウェアとソフトウェア
-結果
1数学モデル
運動方程式の導出は、制御と運動のモデリングをさらに合成するために必要です。 このセクションでは、数学とメカニズムについて少し説明します。
現時点では、球形ロボットのすべての既存の数学モデルは、2次ラグランジュ方程式を使用していくつかの単純化を考慮してコンパイルされています。 また、ballobotは非ホロノミックな機械システムであるため、このようなシステムに第2種のラグランジュ方程式を適用することは正しくありません。 CMUロボットでは、球形ロボットモデルは3つの独立した平面モデルと見なされるため、これらのモデルの相互の影響は考慮されません。 Rezeroは、オムニホイールの回転から生じるジャイロ効果を考慮しない3次元の数学モデルを開発しました。
最小限の仮定でロボットの最も完全な数学モデルを作成するという目標を設定しました。 この目標を達成するために、私のスーパーバイザーS.L. クルチコフ、私は彼に心から感謝しています。
1.1運動学
システムの運動学的説明のために、図に示す移動座標系を紹介しました。
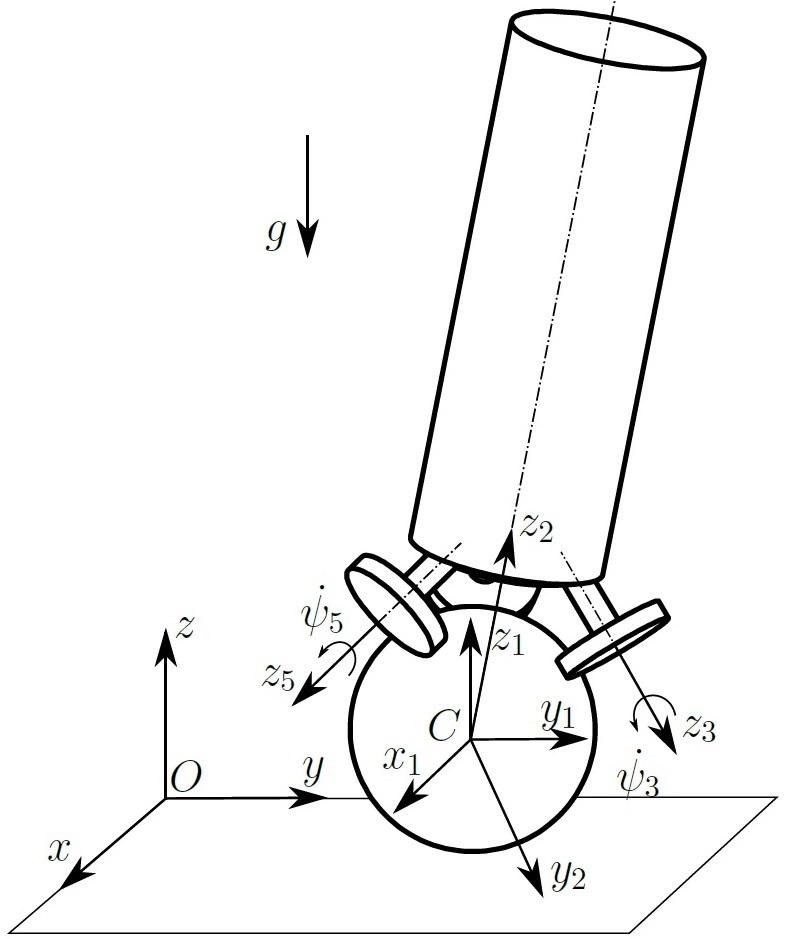
慣性座標系は次のように指定されます 。 座標系
ボールの中心に位置しています。 慣性参照システムからボールの中心に移動するために、次の同次マトリックスが使用されます。
どこで そして
軸に沿ったボールの中心の変位
そして
それに応じて。
ボールの回転を表すには、カルダンアングルまたはテイトブライアンアングルを使用すると便利です。 したがって、座標系 ボールに関連付けられて回すことによって得られます
角に
、
そして
軸周り
そして
それに応じて。 この一連の回転は、回転行列の積として表すことができます。
同様に、宇宙での球形ロボットの本体の回転を記述することができます。 座標系 体に関連付けられた2番目のリンクは、
角に
、
そして
軸周り
そして
それに応じて。 このターンのシーケンスは、回転行列の積として表すこともできます。
3番目、4番目、5番目の座標系はオムニホイールに関連付けられています。 身体の座標系からオムニホイールの座標系に移動するには、一連の基本的な変換(2回転、移動、再度回転)を実行する必要がありますが、ここでは説明しません。
遷移のシーケンスは、次の運動学的グラフの形式で表示されます。

次の一般化された座標のベクトルは、システムの位置を記述するために使用されます。
どこで -ボールの中心の座標、
-ボールと体の回転をそれぞれ表すカルダン角、
-エンジンの軸を中心としたオムニコルの回転角度。
1.2ダイナミクス
システムの非ホロノミーに基づいて、投票の運動の微分方程式を構成するためにAppel方程式を使用することが決定されました。
このシステムは6つの非ホロノミック接続に重ねられています。ボール上の3つのオムニホイールローリングリンク、ボールの中心の速度用の2つのリンク、ボールの回転がない場合の1つの接続です。 したがって、一般化された座標の数はm = 11、結合の数s = 6、および自由度の数n = 5です。 次の擬似速度ベクトルを使用します。
運動方程式をコンパイルするには、各リンクの加速エネルギーを計算する必要があります。
どこで -リンクの数
-慣性座標系から座標系への遷移行列
リンク
-慣性マトリックス
リンク、および
行列のトレースです 。 一般的な場合
の関数です
。 結合方程式を使用すると、加速エネルギーは、
。
ボールの慣性行列は対角形式になります。 座標系の軸 慣性の主な中心軸は次のとおりです。
なぜなら 飛行機 そして
身体の対称面、遠心慣性モーメントです
そして
ゼロに等しい。 身体慣性マトリックスは次の形式になります。
どこで -軸に沿ったボールの中心から体の重心までの距離
。
オムニホール慣性行列は対角形です。 オムニホイール座標系の軸は対称面を形成します。
与えられた慣性モーメントで モーターローターの慣性モーメントを考慮することも必要です。
どこで -ギア比。
擬似座標でのアッペルの運動の微分方程式:
どこで -ドライブの瞬間からの一般化された力、
-重力からの一般化された力。
Appel方程式を行列形式で書き留めて、 :
運動方程式は行列形式で書くことができます
どこで
すべての計算は、Mapleを使用してシンボリックに実行されました。 次に、得られた方程式をシミュレーションのためにMapleからMatlabに転送しました。
2制御アルゴリズムの開発
もう少し制御理論と材料が終わります。 制御理論では、線形システムを分析する方法がよく開発されています。 完全に観測可能なシステムでは、2次関数(線形2次コントローラー、LQR)を使用した最適な制御が最もよく使用され、システムが完全に制御可能な場合、システムの安定化が保証されます。 シャロボットは完全に観察可能なシステムです。なぜなら、 状態ベクトルは完全に測定できます。 可制御性行列のランクを計算すると、システムの可制御性も確信できました。
最初に線形2次コントローラーを取得するには、不安定な平衡の垂直位置の近くでシステムを線形化する必要があります。
ベクトル -状態ベクトルまたは位相ベクトル、
測定のベクトルであり、
-管理(ドライブの瞬間)。
LQRレギュレーターには、次の最適性基準があります。
どこで そして
正定行列です。 この関数を最小化するタスクは、マトリックスのリカッチ代数方程式を解くことになります。
線形2次コントローラーの場合、制御は次のように記述されます。 どこで
、
-リカッチ方程式の解。 結果として、フィードバック係数のマトリックスがあります。
この行列に状態ベクトルを掛けるとき システムを安定させるためにエンジンに適用する必要がある3つのポイントを取得します。 LQRは、状態ベクトルが座標とその導関数で構成される場合、PDレギュレーターです。 ご理解のとおり、従来のPIDコントローラーを使用して、このようなシステムで係数を手動で選択することはほとんど不可能です。
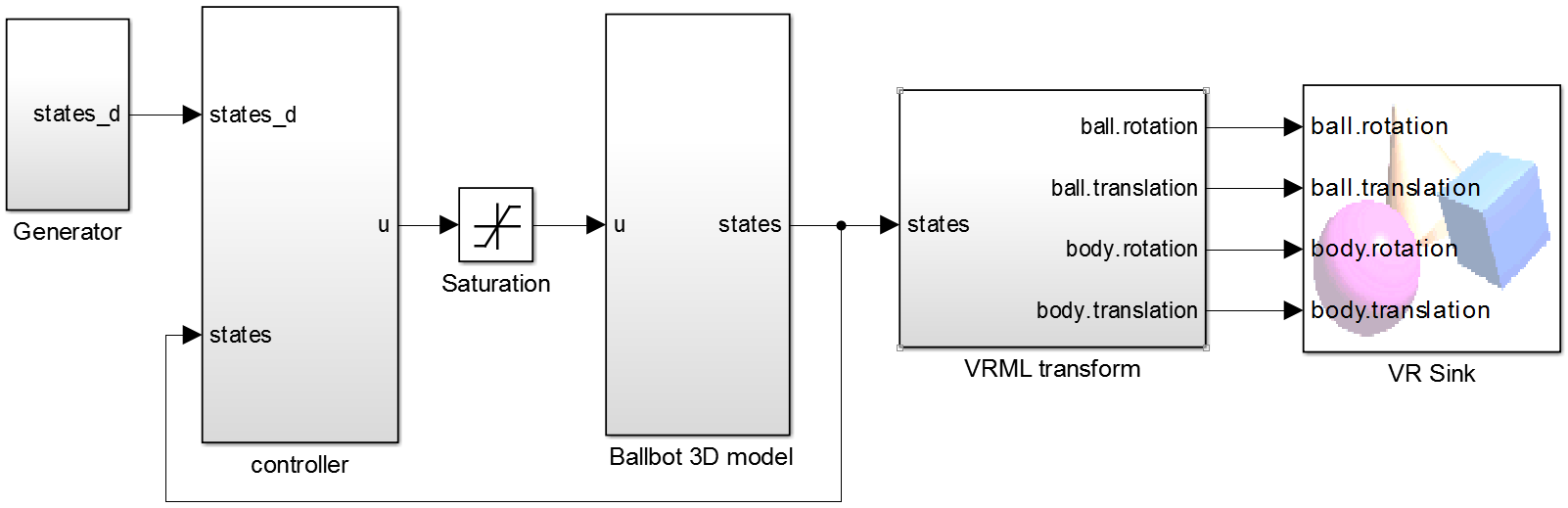
各ブロックについて簡単に説明します。 Ballbot 3Dモデルブロックは、Appel方程式を実装します。 制御入力 (3点)、出力は状態ベクトルです
(条項2を参照)。
VRML変換ブロックは、状態ベクトルを視覚化のための座標に変換します。 「VRシンク」にはvrml形式のモデルが含まれており、このブロックはグラフィックを描画します。
状態ベクトルは、コントローラーブロックの入力に供給されます。 および所望の状態ベクトル
、軌道と速度を設定できます。 このブロックは、3つのポイントを取得するための基本行列乗算を生成します
。
ドライブが開発される瞬間が限られているため、飽和リンクを追加しました。
3次元の視覚化のために、SolidWorksの投票の単純なモデルが作成されました。 次に、vrml形式でエクスポートされ、VR Sinkブロックに追加されました。

初期偏差が10度のシミュレーション結果
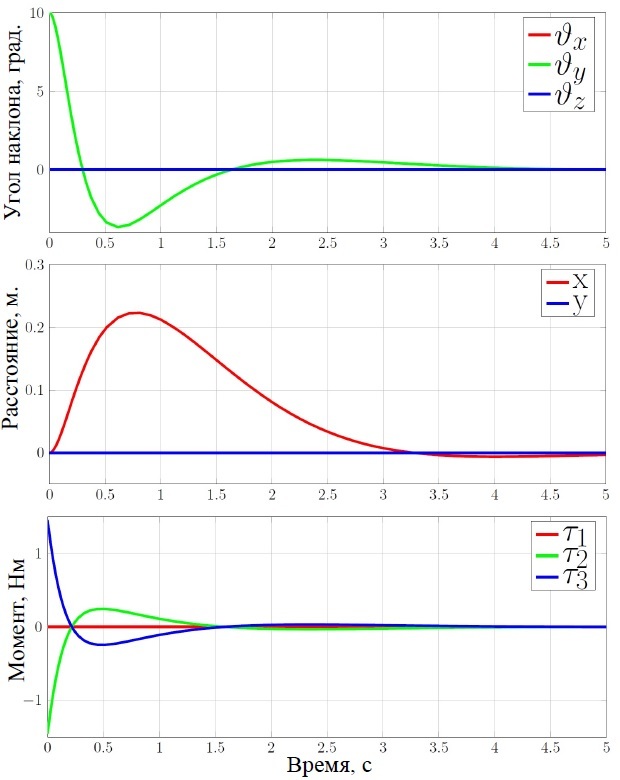
3建設
ロボットの設計は、シーメンスNX CADシステムで開発されました。 構築されたモデルに基づいて、ロボットリンクの質量および慣性特性が決定されました。
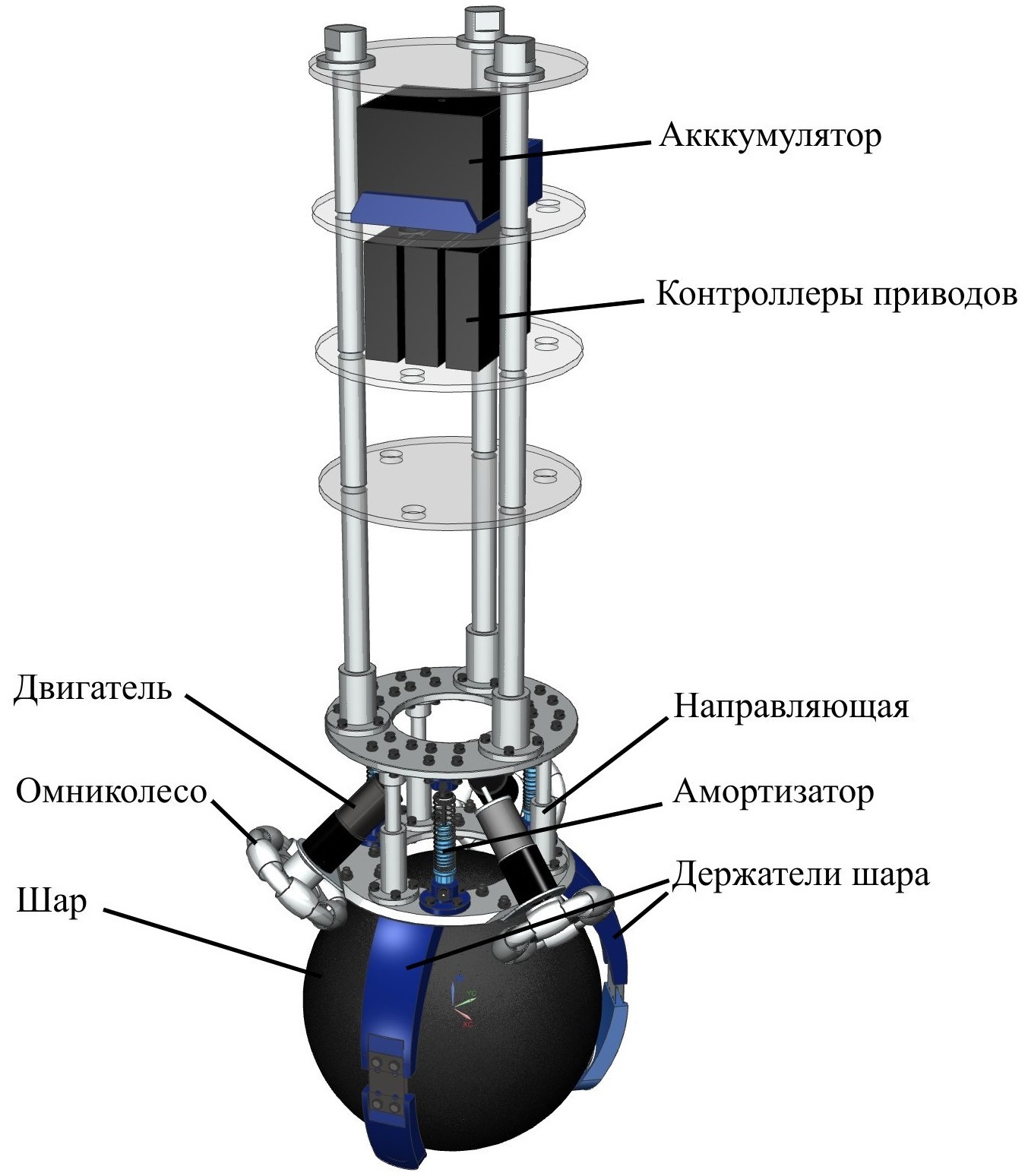
このデザインは、2つのアルミニウム製ベースで構成されています。 オムニホイールを駆動する3つのモーターが下部ベースに固定されています。 上部ベースは、ショックアブソーバーとガイドで底部に取り付けられています。 ショックアブソーバーのタスクは、すべての電子機器が配置されているハウジング上部の振動を低減することでしたが、実際にはこれは役に立ちませんでした。
プレキシガラス製の棚は、建設を容易にします。 バッテリー、ドライブコントローラー、マイクロコントローラー、慣性など、すべてのオンボードエレクトロニクスが含まれています。
直径240 mmのバスケットボールボールがボールとして使用されます。 ボールホルダーはそれをオムニホイールに押し込むため、摩擦が増加します。 残念ながら、私たちの部門には3Dプリンターがなく、注文に応じて印刷するのに費用がかかるため、作成できませんでした。 それらは小さくなく、フィルファクタは強度のために大きく必要です。
Omnikolesは、Aliexpressで120ドルずつ購入しました。 もちろん、ドライブの後のロボットの最も高価な部分です。
すべての金属部品は、モスクワの工場で注文するためにジュラルミンで作られています。 同じ工場で、プレキシガラスの棚を作りました。 注文はおよそ30000rの量で出されました。
友人が、DC-DCコンバーター、IMU、およびI2C用のロジックレベルコンバーターが配置されているボードを分離するのを手伝ってくれました。 ODROIDが上に引っかかっている


これは、ダイナミクセルMX64ドライブを使用した最初の設計です。 ドライブ用の箱が印刷されました。

1:10のスケールのラジコンモデル用のHSPショックアブソーバー。

このフォームでは、ドライブとコントローラーのセットを受け取りました。

オムニホイールをモーターシャフトに取り付けるには、スリーブを研磨しなければなりませんでした。

これが最終結果です。

4ハードウェアとソフトウェア
球形ロボットのほぼすべてのハードウェアコンポーネントは、機能図に表示されます。 下から上に向かって、各要素について少し説明します。

4.1ドライブとドライブコントローラー
誰もがドライブとドライブコントローラーを見つけるのは困難でした。 LQRコントローラーの出力には瞬間があるため、電流を制御できる(つまり、瞬間に応じた)コントローラーが必要です。 どうやら、このタスクは日常生活では非常にまれであり、手頃な価格のソリューションはダイナミクセルのみでした。 現在の制御モードを備えたDynamixel MX64ドライブを購入して試しました。 残念ながら、彼らのパフォーマンスはロボットを安定させるのに十分ではありませんでした。
私はすでに本物の投票を作成する希望を失いましたが、幸いなことにRobotekhnika Research CenterのYaroslavが私たちを助け、しばらくの間3台のMaxonドライブにコントローラーを提供しました。 その結果、次の特性を持つMaxon EC-max 30 40WブラシレスDCモーターになりました。
- 定格電圧24V
- 定格回転速度7220 r / s
- 定格トルク33.8 mNm
- 保持トルク160 mNm
ギア比n = 14のMaxon GP 32遊星ギアボックス、および現在の制御モードを備えたMaxon EPOS 24/5ドライブコントローラー。
ご覧のとおり、ドライブはそれほど強力ではなく、ギア比は小さいため、出力モーメントは投票を安定させるのに十分ではありません。 たとえば、Rezeroは200Wのモーターとギア比が51のギアボックスを使用します。
4.2マイクロコントローラー、慣性モジュール、トランシーバー
マイクロコントローラとして、STM32F4-Discoveryを使用しました。これには、CAN、UART、I2Cなどの必要なインターフェイスがあります。 I2Cを介してジャイロスコープと加速度計からデータを受信し、CANバスを介してエンコーダーからデータを受信します。 受信したデータに基づいて、制御を計算し、CANバス経由でドライブコントローラーにタスクを送信します。 EPOSコントローラとの通信用のプロトコルを自分で実装しないために、 libeposライブラリを使用しました 。 STM'kuをCANネットワークに接続するには、CANトランシーバー(トランシーバー)が4ドル必要です。
慣性モジュールとして、3軸ジャイロスコープと3軸加速度計を含むMPU6050チップに基づいて3ドルでGY-521ボードを使用しました。 これらのセンサーの測定値を処理するために、最近ヘリコプターガイドに愛されているMajwickフィルターを使用しました。
STMでの開発を簡素化するために、STM32Cube HAL(ハードウェアアブストラクションレイヤー)を使用しました。
コントロールが動作する周波数は約300 Hzです。 1秒間に300回、すべてのセンサーの測定値を読み取り、制御を計算して、タスクをドライブに送信します。 これらはすべて無限ループで発生し、次の擬似コードとして表すことができます。
int main() { initialize_imu();/* IMU I2C */ initialize_motors(); /* CAN */ while (1) { read_imu(); /* IMU */ get_omniwheels_speed(); /* CAN */ /* UART odroid */ if (uart_rx_flag) { uart_rx_flag = 0; struct joystick_data* joystick = (struct joystick_data*)UARTdev_Get_RX_buf(); process_joystick_input(joystick); } calculate_control(); /* */ set_torque(); /* CAN */ } }
4.3シングルボードコンピューター、バッテリー、DC-DCコンバーター、ジョイスティック
ODROID U3オンボードシングルボードコンピューターは、Bluetoothアダプターを介してジョイスティックからデータを受信し、UARTを介してマイクロコントローラーに転送します。 Linuxカーネル3.8.13.26-rt31でリアルタイムサポートを備えたlubuntuオペレーティングシステムを実行します。

C = 4.5 Ahの容量を持つ鉛蓄電池Delta 12045。 約1時間の作業に十分です。

Odroid-U3シングルボードコンピューターの電圧は5V、最大消費電流は2Aです。 なぜなら 12V電源、2ドルの降圧LM2596S DC-DCコンバーターが必要です。

バルーンを制御するには、Bluetooth Teriosジョイスティックを使用します。 ジョイスティックは、Asus USB-BT400アダプターがインストールされているODROIDにBluetooth経由でコマンドを送信します。 ジョイスティックコマンドを読み取るために、次のライブラリを使用しました。 受信したコマンドは解析され、パッケージ化され、UARTを介してSTM32に送信され、各バイトで割り込みが発生します。

SSH経由でODROIDに接続することもできます。 起動時に、odroydはWiFiアダプターを介してアドホックネットワークを作成します。
結果
合計で、作業中の投票をまとめることができました。 このプロジェクトを実装するには、正確に2年かかりました。 スイスからの学生のような人的、生産的、財政的なリソースがなかったため、Rezeroの結果に近づくことができなかったとだけ言っておきましょう。 より強力なエンジンとより高度な慣性モジュールがあれば、結果は一桁良くなると思います。
何らかの理由でソースコードを開きません。 実装の詳細を知りたい場合は、私たちに書いてください。私たちはベストプラクティスを共有します。 エンジンは返却されなければならず、現時点では金属片にはエンジンがありません。 適切なエンジンと希望のエンジンがあれば、おそらくプロジェクトは学生によってさらに開発されるでしょう。 たとえば、非線形制御アルゴリズムを開発し、IMUフィルタリングアルゴリズムを改善することは興味深いでしょう。
私は開発プロセスについて非常に表面的に話したので、あなたの質問に喜んで答えます。