わかりやすいように、このデータをグラフィック形式で表示する必要があります。 最初に試すことができるのは「モザイク」です。 ブロックのサイズは、オブジェクトの対応するメトリックの値を反映します。 マトリックスは同一のオブジェクトで構成されているため、「奇妙な」オブジェクトは一般的な背景から目立つはずです。 ただし、メトリックの違いはそれほど大きくないため、「奇妙な」ブロックのサイズは根本的に目立ちません。 これは、次の例(マトリックスと「モザイク」としての表示)から最もよく理解できます。
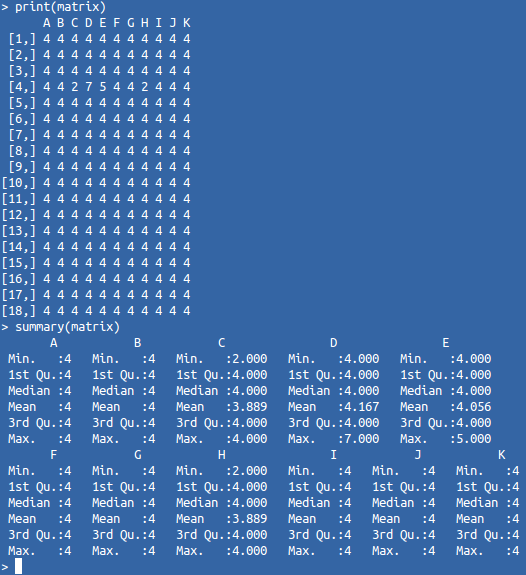
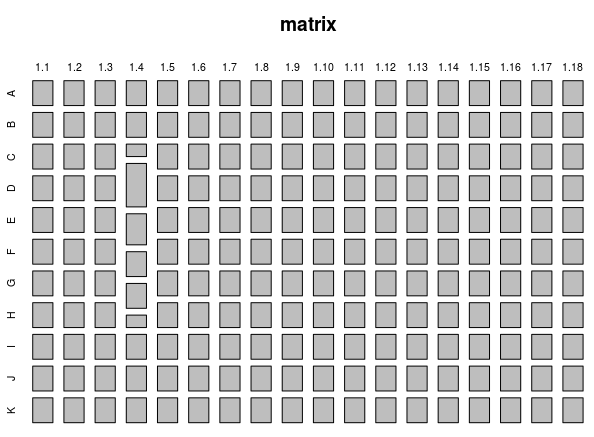
人は、均一な背景に対して色が異なるオブジェクトを非常に迅速に見つけることができることはよく知られています。 したがって、このマトリックスをヒートマップに表示すると、類似した要素が単一の背景を形成し、異なる要素が同質の多数派とよく対比します。
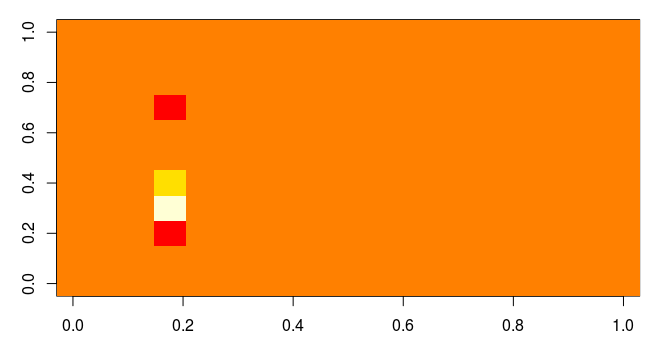
当然、人は色だけでなくオブジェクトの形状も非常によく認識しています。 マトリックスを3次元の遠近法の形式で表示すると、典型的なオブジェクトの総質量からの偏差が非常にはっきりと見えるようになります。
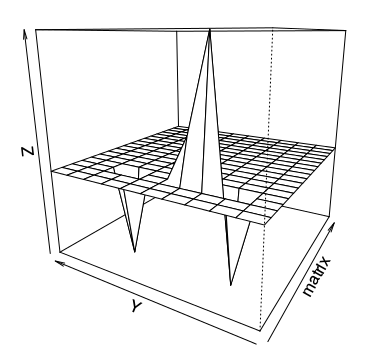
さまざまなオブジェクトの兆候を知っていると、「奇妙な」オブジェクトのみで構成されるサブセットを形成できます。 次に、サブセットのオブジェクトと典型的なセットオブジェクトの違いの図を表示できます。
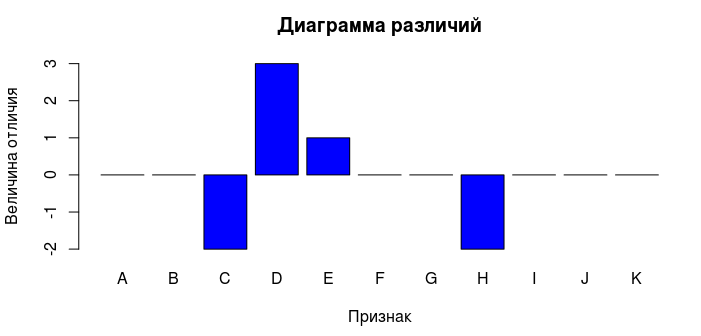
もちろん、関心のあるインジケーターの動作をより詳細に研究することは論理的です。 ご存じのように、線形相関係数は変数の依存関係を見つけるのに必ずしも役立つとは限りませんが、目的の期間のグラフを作成できます。 相関を視覚的に評価することははるかに簡単です。 ただし、グラフを作成するだけでなく、基本的な線形回帰分析を実行してみます。 小さな例を考えてみましょう。 1つの指標が増加すると、それに依存する変数の値が増加するという仮説があります。 これをグラフィカルな形式で表示してみましょう。
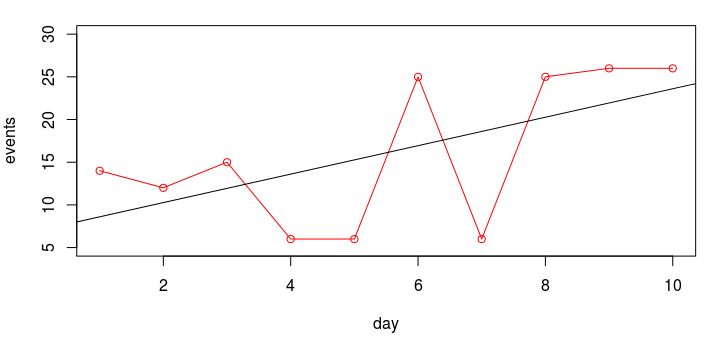
空間内のポイントによって類似性を見つけることができる状況があります。 座標形式(横座標と縦座標)で2つの記号を表示すると、いくつかのポイントがグループ(フォームクラスター)で収集されていることがわかります。 ポイント(A、B、C)は1つのグループに集められ、ポイント(A +、B +、C +)は別のグループに集められます。 そして、Zを追加しますが、これはどのクラスターにも入らないはずです。 これはそのような「孤独な狼」です。 階層的なクラスター分析は、類似点をより明確に表示するのに役立ちます。 グラフと樹状図上の点の表示を比較します。
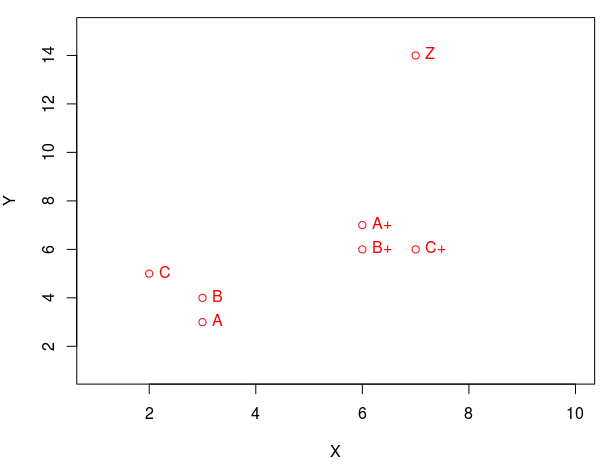
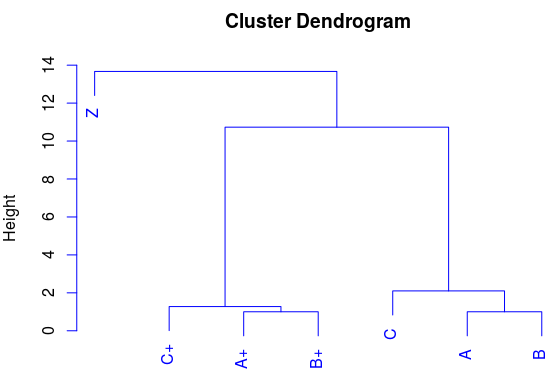
これはかなり普遍的なアプローチであり、比較的少量のデータの視覚的評価によく使用されます。 多くの数学的システムには、すでによく知られているプログラミング言語Rなどの前述のメソッドの実装が既に含まれています。このような問題の解決方法は次のようになります。
# matrix <- as.matrix(read.csv(path), ncol=11, byrow = TRUE) print(matrix) summary(matrix) # mosaicplot(matrix) image(matrix) persp(matrix, phi = 15, theta = 300) # dataset <- subset(matrix, matrix[,"A"] == 4 & matrix[,"C"] < 4 & matrix[,"D"] > 4) print(dataset) # a <- as.vector(dataset[1,], mode='numeric') b <- as.vector(matrix[1,], mode='numeric') diff <- a - b barplot(diff, names.arg = colnames(matrix), xlab = "", ylab = " ", col = "blue", main = " ", border = "black") # day <- c(1:10) events <- c(14, 12, 15, 6, 6, 25, 6, 25, 26, 26) cor.test(day, events) plot(day, events, type = "o", ylim=c(5, 30), col = "red") abline(lm(events ~ day)) # matrix <- matrix(c(3, 3, 2, 6, 6, 7, 7, 3, 4, 5, 7, 6, 6, 14), nrow=7, ncol=2) dimnames(matrix) <- list(c("A", "B", "C", "A+", "B+", "C+", "Z"), c("X", "Y")) plot(matrix, col = "red", ylim=c(1, 15), xlim=c(1, 10)) text(matrix, row.names(matrix), cex=1, pos=4, col="red") plot(hclust(dist(matrix, method = "euclidean"), method="ward"), col = "blue")