🐇 💃🏼 📉 ロスレスデータ圧縮アルゴリズム：市場について彼らが言うこと 🙍 ™️ ◀️

Habréのブログでは、金融市場のさまざまな技術を検討するだけでなく、分析の過程でアナリストが使用するさまざまなツールについても説明しています。特に、それほど前ではないが、ランダムウォーク仮説を金融市場の状態を予測するためにどのように使用できるかについて書いた。 NMRQLヘッジファンドの定量アナリストであるStuart Reedは、チューリングファイナンスのWebサイトで彼の研究結果を公開し、市場仮説のランダム性をテストするためにこの仮説を適用しました。

これは、乱数生成器がNISTテストグループを「実行」して、利益のために市場の非効率性を悪用する脆弱性がどこで発生するかを理解するというものでした。実験中に、著者は、一部の評判の高い科学者が信じているように、単純なコイントスの観点から市場行動を説明できないという結論に達しました。一部のテストでは、市場の振る舞いにおける一定レベルの「ノイズ」を修正することができました。それらの1つ-線形複雑度テスト-は、ランダム性と圧縮度の関係の考えを思い出させるため、著者の注意を引きました。

新しい記事で、Reid は、データ圧縮アルゴリズムが以前に課されたタスクにもたらす利点を理解しようとしました。私たちはあなたの注意にこの作品の適応された翻訳を提示します。

市場パフォーマンスとランダムウォーク仮説

その極端な表現では、市場効率仮説は、価格の価値において、すべての情報が、公的であろうと私的個人にとって入手可能であろうと、即座かつ正確に考慮されると述べています。したがって、現在の相場は現在の状況を正確かつかなり完全に反映しているため、明日の価格予測は市場の現在の状態に基づいている必要があります。

この理論によると、過去の詳細な経済分析やファンダメンタル分析は、将来のより正確な予測を提供しません。情報の完全性と十分性という点で効率的な市場では、「明日」に見える未知のデータに依存するため、未来は定義されていません。今日のオブザーバーの位置に基づいて、将来の変更はランダムです。時間内に旅行する方法を知っているアナリストのみが市場を「ハッキング」できます。

この仮説には、状況のより複雑な理解、進化的および行動的要因の影響を提唱したとしても、そのメリットがあります。この理論のメリットは否定できません。まず、市場の動きを予測するのは本当に難しいです。第二に、平均的なプレーヤーが市場を破ることができる一連のアクションが本当にありません。第三に、効率性仮説は、例えばデリバティブなどの金融革新の出現を非常に論理的に説明します。

効率性仮説に対する最も深刻な批判は、行動の財務分析から来ており、これはその基本的な仮説に疑問を投げかけています。このアプローチの一環として、投資家は合理的に行動せず、株式に「公正な」価格を与えることができないと主張されています。実際には、プレイヤーは価格について一般的な期待を持ちません。

市場開発の進化論は、これにいくつかの議論を追加します。彼女は、このシステムは、進化の法則に従って、相互作用する異種のエージェントで構成されていると考えています。この相互作用では、ランダム性、勢い、価値、資産回転率（反転）が前面に出ます。これらの評価基準のいずれも、他に勝るものはありません。プレイヤーが彼らの影響に適応するにつれて、市場状況への影響は変わります。効率性仮説では、こうしたものを市場の異常と呼びますが、これは完全に真実ではありません。それらの外観は非常に予測可能であり、市場への影響を定量化できます。

批判に応えて、市場効率の支持者は2つの新しい仮説を立てました。公開情報のみが引用符に反映されていると主張する人もいます。もう1つは、現在の株価に対する履歴データの影響を認識することです。しかし、主な位置は同じままです。価格の動きは、マルコフ連鎖、ランダムウォークの分布に従います。

ほぼすべての現代の価格モデルの根底にあるランダムウォーク仮説を複製していることがわかります。学者と市場の実践者は、市場の相対的な有効性とランダム性を研究するために数十年を費やしています。前の記事で、Stuart Reedは、ランダム性をチェックするテストの1つ、LoおよびMcKinleyの不均一分散関係テストを紹介しました。今回は、とりわけ、Lempel-Ziv圧縮アルゴリズムに焦点を当てます。

アルゴリズム情報理論とランダムネス

定量分析では、ランダム性の研究は新しいものではありません。暗号化、量子力学、および遺伝学はこれを長い間行ってきました。当然のことながら、これらの科学からいくつかのアイデアやアプローチが取り入れられました。たとえば、エコノミストは、情報のアルゴリズム理論から、ランダムシーケンスは非圧縮性であるという考えを取り入れています。まず、この興味深い考えの背景を確立してみましょう。

1930年代、Alan Turingは自動計算機と呼ばれる抽象的な計算モデルを導入しました。今日では、チューリングマシンとして知られています。この点で、私たちは次の声明にのみ興味があります。「どの計算アルゴリズムが定められているかは関係ありません。マシンはアルゴリズム自体のロジックを模倣する必要があります。」

チューリングマシンモデル

簡略化された形式では、アルゴリズムは入力データのセットを出力のセットに変換するための決定論的な一連のステップです。フィボナッチ数列に対してこのようなアルゴリズムを構築するのは簡単です。次の数は前の2つの数の合計です。別の偉大な数学者アンドレイ・コルモゴロフによると、シーケンスの複雑さは、このシーケンスを出力として生成する最短の計算プログラムの長さによって測定できます。このプログラムが元のシーケンスよりも短い場合は、シーケンスを圧縮、つまりエンコードします。

チューリングマシンにランダムシーケンスSを入れるとどうなりますか？データの配布にロジックがない場合、マシンにはシミュレートするものがありません。ランダムシーケンスを取得する唯一の方法はprint Sです。ただし、このプログラムはランダムシーケンスSよりも長くなります。したがって、その複雑さは定義により高くなります。これは、ランダムシーケンスが非圧縮性であると言うときの意味です。別の質問、見つけたプログラムが最短であるという事実をどのように確認できますか？この結論に到達するために、無限の組み合わせを整理する必要があります。

簡単に言えば、コルモゴロフの複雑さは計算できません。したがって、ランダム性は計算できません。シーケンスがランダムであることを証明することはできません。しかし、これは、シーケンスがランダムである可能性をテストできないという意味ではありません。ここで、統計的ランダム性テストが登場し、その一部は圧縮アルゴリズムを使用しています。

圧縮と市場のランダム性：問題の説明

市場のパフォーマンスをテストするために圧縮アルゴリズムを適合させようとした科学者はわずかです。アイデア自体は単純ですが、この単純さの背後に特定の課題が隠されています。

課題1：有限シーケンスと無限大

情報理論におけるランダム性の定義は、無限の範囲に対処する必要があることを意味します。確率のみに基づいて、任意の有限シーケンスをすでにわずかに圧縮できます。市場で比較的短いシーケンスをチェックするために圧縮を使用する場合、アルゴリズムがそれらを圧縮できるかどうかは気にしません。圧縮率が統計的に有意になるかどうか疑問に思っています。

課題2：市場のドリフト

ランダム性にはいくつかの種類があります。最初のタイプは、マルチンゲールまたはコルモゴロフの本当の事故と呼ばれます。ほとんどの場合、コンピューターサイエンスと情報理論に関連しています。 2番目のタイプは、金融分析およびランダムウォーク仮説で使用されるマルコフランダムネスです。

これは、市場のランダム性の統計的検定を選択する際には非常に注意しなければならないことを意味します。最初のタイプのランダム性のために設計された統計的検定は、マルコフランダム検定とは異なる信頼区間を持ちます。

これで少しクリアになります。ブラウン運動と非ゼロ偏差の幾何学的ブラウン運動の2つのモデルがあるとします。この例では、最初のモデルは両方のタイプのランダム性に適しています。 2番目は、マルコフのチャンスのためだけです。 2番目のモデルのテスト結果は歪められます。

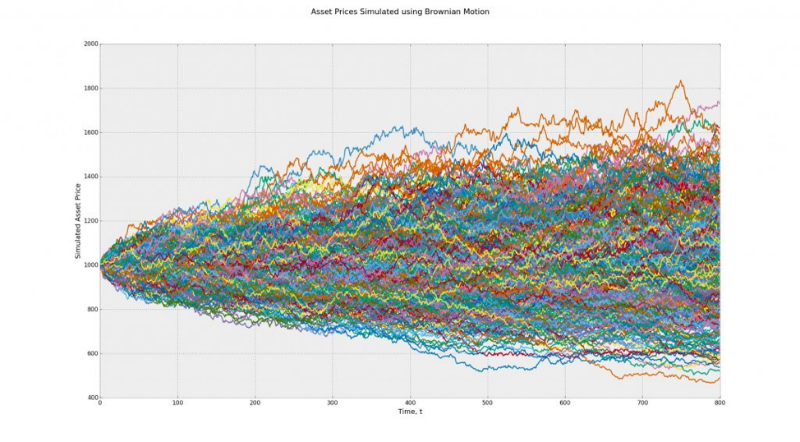
モデル1（ブラウン運動）-平均して、すべての経路はどこにも導かれず、偏差はゼロです。 二値化により、このモデルはコインフリップシーケンスに変わります

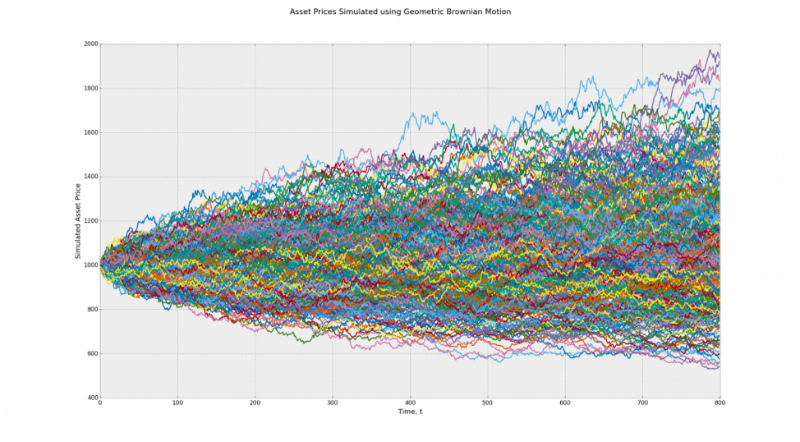
モデル2（幾何学的なブラウン運動）-経路が進み、偏差はゼロではありません。 二値化中に、結果に歪みが導入されます

これは、ランダムウォークスルー圧縮の仮説に反論したい人にとって深刻な問題です。理論は、市場のドリフトの過度の予測可能性、つまり、誰かが市場を破る能力のみを扱っているためです。

課題3：確率的ボラティリティとギャップ

次の問題は、ボラティリティの不安定性が、特定の市場の動きが理論的計算に反して、規則的で頻繁な現象のように見えるという事実につながる可能性があることです。この問題は「厚い尾」とも呼ばれます。ギャップや確率的ボラティリティに関係なく、市場の変化のノイズがゼロになる傾向があると仮定すると、バイナリコードの変化を想像して問題を解決できます。

市場のランダム性の圧縮テスト

アカデミックサイエンスでは、ロスレスデータ圧縮アルゴリズムが市場のパフォーマンスを評価するためにすでに適用されています。ほとんどの研究の本質は次のとおりです。先進市場は高レベルの効率性を示し、新興市場は過度の圧縮性と一定レベルの非効率性を示します。これらの非効果は、特定の時間間隔で予想されるよりも高い確率のレベルを示す特定のパターンによってのみ説明できます。

検証方法

方法論は、3つのよく知られた圧縮アルゴリズムに基づいています：{gzip、bzip2およびxz}。

Quandl.comからマーケットインデックスをダウンロードする必要があります。
次に、インデックスの対数リターンを計算し、rとして指定します。
それらの平均（偏差成分）-μrを計算します。
指向性（トレンド）を除去するには、rμrを減算します。
次に、rはバイナリシステムに変換され、ゼロより大きい値を1で置き換え、ゼロより小さい値をそれぞれゼロで置き換えます。
次に、rは、個別のウィンドウのインポジションによってmに分割されます-Wはそれぞれ7年間です。
各ウィンドウは16進数のwh（4日間のサブシーケンス）に変換されます。
各w _h 、w _hcは圧縮され、圧縮係数が計算されます。
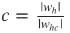この平均は、すべてのウィンドウ-c ^∗に分散されます。
予想される圧縮率は、擬似ランダムデータ-E [c ∗]を使用して計算されます。
c ^∗ > = min（1.0、E [c ^∗ ]）の場合、市場は過度の圧縮性を示さず、これはその有効性を意味します。
c ^∗ <min（1.0、E [c ^∗ ]）の場合、過度の圧縮率が存在し、市場の非効率性を意味します。

Rテストおよび解析アルゴリズム

RにはmemCompressおよびmemDecompress関数が既にあるため、このようなテストを行うのにそれほど多くのコードは必要ありませんでした。 Pythonにも同様の機能があります。

compressionTest <- function(code, years = 7, algo = "g") { # The generic Quandl API key for TuringFinance. Quandl.api_key("t6Rn1d5N1W6Qt4jJq_zC") # Download the raw price data. data <- Quandl(code, rows = -1, type = "xts") # Extract the variable we are interested in. ix.ac <- which(colnames(data) == "Adjusted Close") if (length(ix.ac) == 0) ix.ac <- which(colnames(data) == "Close") ix.rate <- which(colnames(data) == "Rate") closes <- data[ ,max(ix.ac, ix.rate)] # Get the month endpoints. monthends <- endpoints(closes) monthends <- monthends[2:length(monthends) - 1] # Observed compression ratios. cratios <- c() for (t in ((12 * years) + 1):length(monthends)) { # Extract a window of length equal to years. window <- closes[monthends[t - (12 * years)]:monthends[t]] # Compute detrended log returns. returns <- Return.calculate(window, method = "log") returns <- na.omit(returns) - mean(returns, na.rm = T) # Binarize the returns. returns[returns < 0] <- 0 returns[returns > 0] <- 1 # Convert into raw hexadecimal. hexrets <- bin2rawhex(returns) # Compute the compression ratio cratios <- c(cratios, length(memCompress(hexrets)) / length(hexrets)) } # Expected compression ratios. ecratios <- c() for (i in 1:length(cratios)) { # Generate some benchmark returns. returns <- rnorm(252 * years) # Binarize the returns. returns[returns < 0] <- 0 returns[returns > 0] <- 1 # Convert into raw hexadecimal. hexrets <- bin2rawhex(returns) # Compute the compression ratio ecratios <- c(ecratios, length(memCompress(hexrets)) / length(hexrets)) } if (mean(cratios) >= min(1.0, mean(ecratios))) { print(paste("Dataset:", code, "is not compressible { c =", mean(cratios), "} --> efficient.")) } else { print(paste("Dataset:", code, "is compressible { c =", mean(cratios), "} --> inefficient.")) } } bin2rawhex <- function(bindata) { bindata <- as.numeric(as.vector(bindata)) lbindata <- split(bindata, ceiling(seq_along(bindata)/4)) hexdata <- as.vector(unlist(mclapply(lbindata, bin2hex))) hexdata <- paste(hexdata, sep = "", collapse = "") hexdata <- substring(hexdata, seq(1, nchar(hexdata), 2), seq(2, nchar(hexdata), 2)) return(as.raw(as.hexmode(hexdata))) }

Githubコード

以下は、圧縮アルゴリズムで使用される3つの圧縮スキームの簡単な説明です。

Gzip圧縮 LZ1とハフマンのエンコードを組み合わせたDEFLATEアルゴリズムに基づいています。 LZ1は、アブラハムレンペルとジェイコブジブにちなんで命名されました。シーケンス内の繰り返しパターンを置き換え、これらのパターンのコピーへのリンクを元の非圧縮バージョンに配置することで機能します。各一致は、デコーダーに関する次の情報を含む長いペアを介してエンコードされます。パラメーターyは、その後の距離xのすべてのパラメーターと等しくなります。 David Huffmanにちなんで名付けられた2番目のアルゴリズムは、シーケンス内のパターンの出現頻度によって最適なプレフィックスツリーを構築します。
BZIP2圧縮 。 Burroughs-Wheeler変換、motion-to-start変換（MTF）、およびHuffmanコーディングの3つの圧縮メカニズムを使用します。これらの最初の方法は、シーケンスを類似の文字のストリームに再配置して、標準的な方法で圧縮手順を簡素化する可逆的な方法です。 MTF変換は、シーケンス内の文字をスタック上のインデックスに置き換えます。したがって、同じ文字の長いシーケンスは小さい数字に置き換えられ、まれな文字は大きな文字に置き換えられます。
XZ圧縮 。これは、7z圧縮形式で開発された一連のLempel-Ziv-Markovアルゴリズムを通じて機能します。これは基本的に、LZ1アルゴリズムに続く語彙圧縮アルゴリズムです。その出力は、適応バイナリレンジエンコーダーと呼ばれる、各ビットの確率的予測を提供するモデルを使用してエンコードされます。

たとえば、3つのアルゴリズムはすべて、関数memCompressおよびmemDecompressを介してR言語で使用できます。これらの関数の唯一の問題は、入力が16進シーケンスの形式で与えられなければならないことです。 bin2rawhex関数を使用して変換できます。

結果とそのo（悪魔）の意味

実験では、51のグローバル市場インデックスと12の通貨ペアが使用されました。シーケンスは、毎週および毎日の頻度でテストされました。

すべてのアセットは、ウォークフォワード手法を使用したgzip、bzip2、およびxzアルゴリズムを使用して圧縮されました。ドル/ルーブルのペアを除き、どの資産も過度の圧縮性を示しませんでした。実際、それらのどれも圧縮性をまったく示しませんでした。これらの結果は、線形複雑度テストを使用した過去の実験の結果を裏付けました。しかし、NISTテストの結果とLo-McKinleyテストの結果は矛盾しています。理由を理解する必要があります。

オプション1。最初の結論は、グローバル市場が比較的効率的であることを（学者を喜ばせるために）認識することです。それらの動作は非常にランダムに見えます。

オプション2。または、金融市場の効率とランダム性のチェックに関連して、データ損失のない圧縮アルゴリズムに間違いがあることを認めることができます。

これらの仮説をテストするために、実験の著者は圧縮テストをテストするテストを開発する必要がありました。

圧縮試験

実際、ランダムウォーク仮説の反対者は、100％の市場決定論を主張していません。ポイントは、市場の行動が100％ランダムではないことを証明することです。つまり、市場にはシグナルとノイズの2つの側面があります。信号は何百もの異常として現れ、ノイズは明らかな一致と効率として機能します。これらはコインの両面です。次のステップは、システムによって生成されるノイズが信号を相殺しないことを認識することです。そのような信号を見つけて使用することにより、市場を「ハッキング」する機会が残っています。

前述に基づいて、著者は圧縮テストをテストするために次の式を提供します。

ノイズ成分の標準偏差--tのサイズを大きくすると、市場の圧縮性がどのように悪化し始めるのかがわかります。標準偏差が0.01マークを超えると、圧縮テストは失敗し始めます。

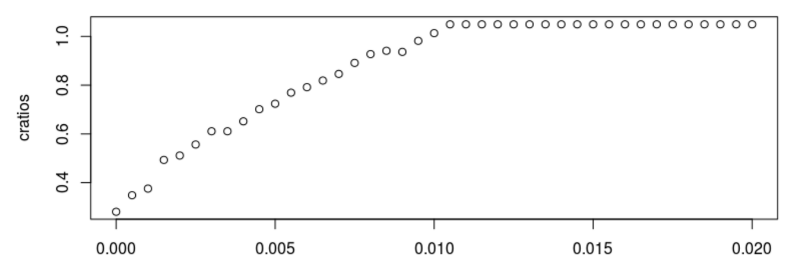
σ= 0.010、σ= 0.020およびσ= 0.040のテストの結論の例は次のとおりです。

圧縮テストでは、これらの市場はすべてデータ損失なしに圧縮アルゴリズムで圧縮できないため、ランダムまたは効率的です。はい、それらはランダムに見えるかもしれません。しかし、それらは信号とノイズで構成されているため、ランダム性を完全にすることはできません。

より適切なチェックを行うには、平均に戻すためにベット戦略/アルゴリズムを使用する必要があります。

結論：ウィンドウサイズw = 4;
時間パラメータtについて、過去wマイナス日t-cへの累積リターンを計算します。
<0,0の場合、資産の100％を保持します（資産が上がると確信しています）。
その他の場合は、共有を削除します。

以下は、各ノイズレベルの2つの図です。最初のものは、平均レート戦略への回帰によって生成された30の株価曲線を示しています。 2番目の例は、戦略の適用による収入と比較した、前の例の平均市場収入を示しています。

これは簡単な例ですが、矛盾を特定するのに役立ちます。

市場が圧迫されていない場合、それは効果的であるということになりますが、それが本当に効果的である場合、それを「ハッキングする」賭け戦略を適用することは不可能です。

ランダム性は証明できないため、シーケンスは実際にはランダムではないため、これを「理解して許す」必要があります。著者によると、圧縮テストは取引戦略よりもノイズに敏感であるため失敗しました（シミュレーションでは、ノイズに対して10倍の感度が得られます）。理由は、データ損失のない圧縮アルゴリズムの使用かもしれません。

検証テストのコードはこちらにあります。

結論

この研究は、圧縮アルゴリズムを使用して市場のランダム性をテストする方法のアイデアを提示し、これが市場の有効性を理解することを示しています。次に、「メタテスト」が開始されました。これは、ノイズに対するこのようなテストの感度が高いことを示しています。その結果、いくつかの結論を出すことができます。

トレンド除去後、市場は十分なノイズを示し始め、データ損失のない圧縮アルゴリズム（gzip、bzip2、xz）に対して「通過不能」になります。
ノイズに対するテストの感度が取引戦略の感度よりも高い場合（記事の例では、そのようなテストは単純な賭け戦略よりもノイズに対して10倍敏感であることが判明しました）、否定的な結果は分析された市場が効果的であることを意味しません。「ハッキング」できないという意味で。
言い換えれば、そのようなテストは、ランダムな市場のanderの仮説の厳密な解釈を主張する学者の正しさを証明しない。一見したところよりも複雑であることが判明しました。
市場のランダム性を決定する統計的テストは、サイズ、リーチ、および感度が異なります。信頼できる結果が得られるのは、いくつかのテストの組み合わせのみです。

ロスレスデータ圧縮アルゴリズム：市場について彼らが言うこと