🧑🏽‍🤝‍🧑🏼 🤚🏾 👰🏽 FPGAカオスジェネレーター 🕵🏻 👨🏼‍🔧 🏴󠁧󠁢󠁳󠁣󠁴󠁿

みなさんこんにちは！

この記事では、カオスの世界の驚くべき機能に焦点を当てています。このような奇妙で複雑なことを混oticとしたプロセスとして抑制する方法についてお話しし、独自の単純なカオスジェネレータを作成する方法を学びます。あなたと一緒に、私たちはドライ理論から宇宙のカオス過程の美しい視覚化に進みます。特に、よく知られているカオスアトラクターの例を使用して、動的システムを作成し、プログラマブルロジック集積回路（FPGA）に関連する問題でそれらを使用する方法を示します。

はじめに

カオス理論は、非線形力学系の振る舞いを記述する珍しい若い科学です。カオスの理論は、その始まりの過程で、単に現代科学をひっくり返しました！それは科学者の心を刺激し、カオスとその特性の研究にますます没頭させました。ランダムプロセスであるノイズとは異なり、カオスは決定論的です。つまり、カオスには、カオス過程を記述するための方程式に含まれる量の変動の法則があります。この定義では、カオスは関数として記述された他の振動と何の違いもないようです。しかし、これはそうではありません。カオス系は初期状態に非常に敏感であり、わずかな変化でも大きな違いが生じる可能性があります。これらの違いは非常に大きいため、1つ以上のシステムが調査されたかどうかを判断することはできません。一般的な科学資料から、このカオス特性は「 バタフライ効果 」と呼ばれるプロセスを最もよく説明しています。多くの人が彼のことを聞いて、本を読んだり、バタフライ効果を使ったテクニックを使った映画を見たりした。本質的に、バタフライ効果はカオスの主な特性を反映しています。

カオス分野の先駆者の一人であるアメリカの科学者エドワード・ローレンツはかつてこう言った。

アイオワで蝶が羽ばたくと、インドネシアの雨季に頂点に達する雪崩の影響を引き起こす可能性があります。

それで、私たちはカオスの理論に飛び込み、即興の手段がカオスを生成することができるものを見ていきます。

理論

主な資料を提示する前に、この記事のいくつかのポイントを理解し、明確にするのに役立つ定義を提供したいと思います。

動的システムは、時間座標とシステムの各要素の位相空間内の位置との間の機能的関係が与えられる要素の特定のセットです。簡単に言えば、動的システムとは、空間の状態が時間とともに変化するシステムです。

自然界の多くの物理的プロセスは、動的システムである方程式系によって記述されます。たとえば、これらは燃焼のプロセス、液体と気体の流れ、磁場と電気振動の振る舞い、化学反応、気象現象、動植物の個体数の変化、海流の乱れ、惑星、さらには銀河の動きです。ご覧のように、多くの物理現象はある程度カオス的なプロセスとして説明できます。

位相ポートレートは、各点が特定の瞬間の動的システムの状態に対応する座標平面です。つまり、これはシステムの空間モデルです（2次元、3次元、または4次元以上の場合もあります）。

アトラクタは、時間の経過とともにすべての軌跡がこのセットに引き付けられる、動的システムの位相空間の特定のセットです。非常に単純な言語の場合、これは空間内のシステムの動作が集中する領域です。多くのカオスプロセスは、特定の空間領域に集中しているため、アトラクタです。

実装

この記事では、ローレンツ、レスラー、リキタケ、ノーズフーバーの4つの主要なアトラクタについてお話します。理論的な説明に加えて、この記事では、 MATLAB Simulinkでの動的システムの作成と、 System Generatorツールを使用したザイリンクス FPGAへのさらなる統合の側面を反映しています。なぜVHDL / Verilogではないのですか？アトラクタはRTL言語を使用して合成することもできますが、すべてのプロセスをより良く視覚化するには、MATLABが理想的なオプションです。リアプノフ指数のスペクトルの計算やポアンカレ断面の構築に関連する困難な点には触れません。さらに、面倒な数学の公式や結論はありません。それでは始めましょう。

カオスジェネレータを作成するには、次のソフトウェアが必要です。

SimulinkおよびDSP Toolboxのライセンスを取得したMATLAB R2014。
ザイリンクスISE Design Suite 14.7ライセンスシステムジェネレーター（DSPエディション）

これらのプログラムは非常に重いため、インストールする際には辛抱強く待ってください。 MATLABでインストールを開始してから、ザイリンクスソフトウェアをインストールすることをお勧めします（別のシーケンスでは、一部の友人が1つのアプリケーションを別のアプリケーションに統合できませんでした）。後者をインストールすると、ウィンドウが表示され、SimulinkとSystem Generatorをリンクできます。インストールには複雑で異常なものはないため、このプロセスは省略されます。

誘引者ローレンツ

ローレンツアトラクターは、おそらくカオス理論で最も有名な力学系です。数十年にわたり、さまざまな物理的プロセスの記述について多くの研究者の注目を集めてきました。アトラクターの最初の言及は、1963年に大気現象のモデリングに携わったE. Lorenzの作品で述べられています。ローレンツアトラクタは、1次の非線形自律微分方程式の3次元動的システムです。複雑なトポロジ構造を持ち、漸近的に安定で、リアプノフ安定です。ローレンツアトラクターは、次の微分方程式系で記述されます。

式では、パラメータの上にあるドットは、時間の経過に伴う量の変化率（微分の物理的意味）を反映する微分の取得を意味します。

パラメーター値σ = 10、 r = 28、およびb = 8/3の場合、この単純な動的システムはE. Lorenzによって取得されました。長い間、彼はシステムが混chaとした特性を示していることに最終的に気づくまで、コンピューターで何が起こっていたのか理解できませんでした！これは、流体の対流をモデル化する問題の実験の過程で得られました。さらに、この動的システムは、次の物理プロセスの動作を説明します。

-シングルモードレーザーのモデル、
-閉ループと平坦な層での対流、
-水車の回転、
-慣性非線形性を備えた高調波発振器、
-雲の塊などの乱流

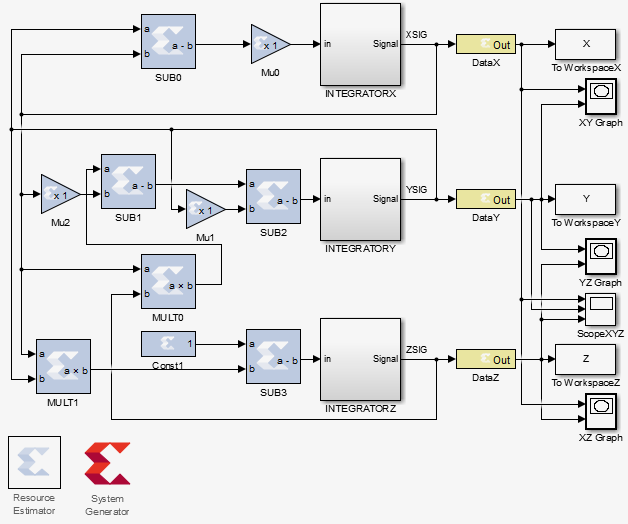
次の図は、MATLABのローレンツアトラクターシステムを示しています。

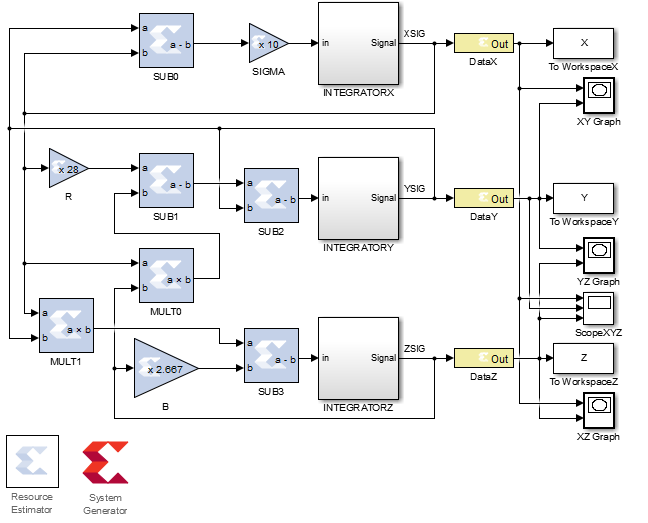
図では次の表記が使用されています。

減算器： SUB0-3 ;
定数乗数： SIGMA、B、R ;
乗数： MULT0-1 ;
初期条件を設定するためのセルを持つ積分器： INTEGRATOR X、Y、Z ;
OUT出力ポート： XSIG、YSIG、ZSIG信号の場合はDATA X、Y、Z 。

さらに、図は補助分析ツールを示しています。これらは次のとおりです。

計算結果をファイルに保存： ワークスペースX、Y、Zへ 。
空間グラフ： グラフXY、YZ、XZ 。
タイムラインのプロット： スコープXYZ ;
水晶の占有リソースを評価し、 Resource EstimatorおよびSystem GeneratorモデルからHDLコードを生成するためのツール。

数学演算の各ノード内では、中間データの長さとそのタイプを示す必要があります。残念ながら、浮動小数点を備えたFPGAを使用するのはそれほど簡単ではなく、ほとんどの場合、すべての操作は固定小数点形式で実行されます。パラメータの誤った設定は、誤った結果につながり、システムを構築するときにあなたを混乱させる可能性があります。さまざまな値を試してみましたが、次のデータ型で解決しました。固定小数点形式の符号付き数値の32ビットベクトル。整数部には12ビット、小数部には20ビットが割り当てられます。

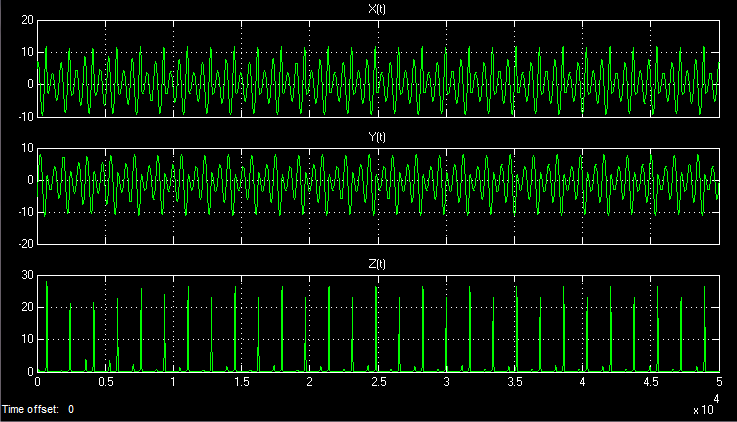
トリガーブロックの積分器X、Y、Zにシステムの初期値、たとえば{10、0、0}を設定して、モデルを起動しました。タイムベースでは、次の3つの信号を観察できます。

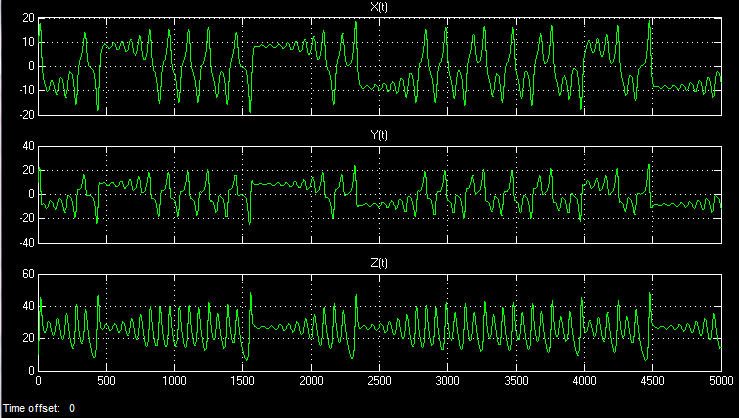
モデリング時間が無限になっても、時間の実現は繰り返されません。カオス的プロセスは非周期的です。

3次元空間では、ローレンツアトラクターは次のとおりです。

アトラクタには2つの引力点があり、その周囲でプロセス全体が行われていることがわかります。初期条件がわずかに変更されると、プロセスもこれらのポイントに集中しますが、その軌跡は以前のバージョンとは大きく異なります。

レスラーアトラクタ

科学記事や出版物で2番目に大きなアトラクター。 レスラーのアトラクターは 、カオス的または周期的な特性の発現の境界点の存在によって特徴付けられます。動的システムの特定のパラメーターでは、振動は周期的でなくなり、カオス振動が発生します。レスラーアトラクタの注目すべき特性の1つは、位相面のフラクタル構造、つまり自己相似性の現象です。原則として、他のアトラクタがこのプロパティを所有していることに注意できます。

レスラーのアトラクターは多くのシステムで観察されます。たとえば、流体の流れを説明したり、さまざまな化学反応や分子プロセスの動作を説明したりするために使用されます。レスラーシステムは、次の微分方程式で記述されます。

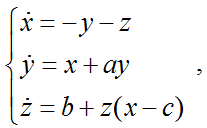
MATLABでは、アトラクターは次のように構築されます。

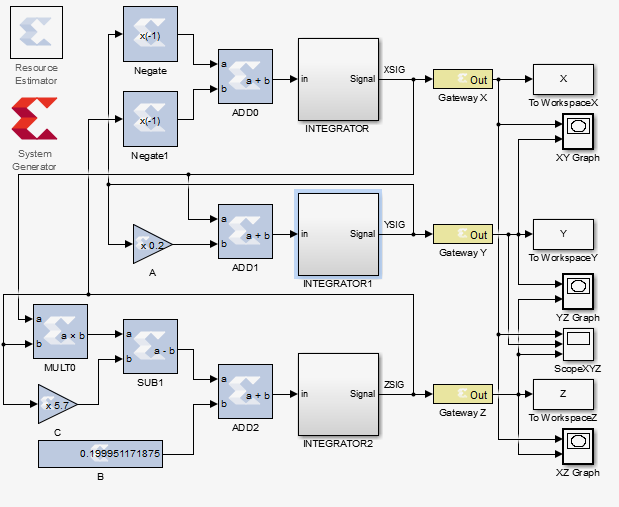
空間量の一時的な実装：

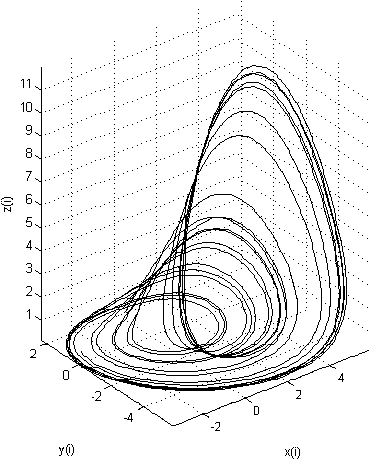
レスラーアトラクタの3次元モデル：

バム！ 値はわずかに変更されました。

初期条件がわずかに変更された場合のアトラクタ（軌道は異なります！）

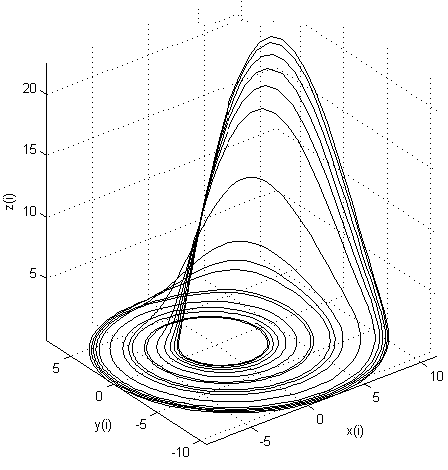
方程式系の他の係数を持つアトラクター（カオスプロセスは周期的なものに変わりました！）

さまざまな初期条件と方程式系の係数の下での3次元アトラクタの画像を比較します。最初のケースで軌道がどれほど劇的に変化したかを見てください。とにかく、それらは単一の魅力的なエリアの近くに集中しています。 2番目のケースでは、アトラクタは一般にカオスの兆候を示しなくなり、閉じた周期ループ（リミットサイクル）に変わりました。

アトラクタ力武

Dynamo Rikitakeは、カオス的な振る舞いをする有名な3次力学系の1つです。これはダブルディスクダイナモのモデルであり、地球の地磁気場のカオス反転の問題で最初に提案されました。科学者のリキタケは、1つのディスクコイルから別のコイルに電流が流れて2番目のディスクを生成するように構築された2つの相互接続されたディスクを持つダイナモシステムを調査しました。ある時点で、システムがクラッシュし、予測できないものが表示され始めました。アトラクタの活発な研究により、リキタケダイナモを、地球のコアにある大きな磁場の渦を結合するモデルに投影することが可能になりました。

Dynamo Rikitakeは、次の方程式系で記述されます。

MATLABのRikitake Dynamoモデル：

一時的な実装：

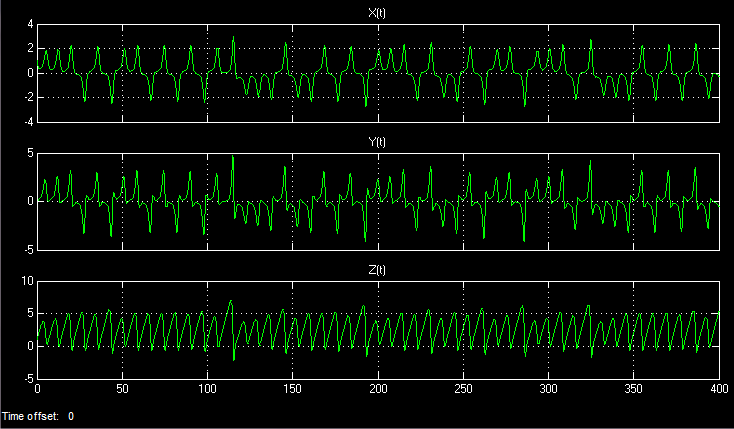
アトラクター（最初のバージョン）：

Dynamo（第2バージョン）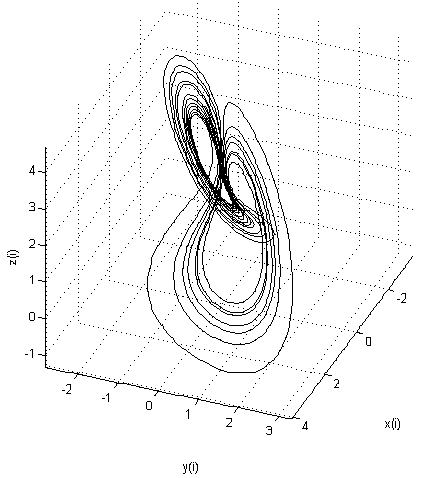

ダイナモのリキタケはローレンツアトラクタにいくらか似ていることに気付くかもしれませんが、これらは完全に異なるシステムであり、異なる物理プロセスを記述しています！

アトラクタノーズフーバー

それほど有名ではありませんが、それほど重要ではない3次元動的システムは、 ノーズフーバーサーモスタットです。分子理論では、時間可逆性のサーモスタットシステムとして使用されます。残念ながら、他の人ほどこのアトラクタについてあまり知りませんが、私はそれを面白いと思い、レビューに含めました。

Nose-Hooverサーモスタットは、次の連立方程式で記述されます。

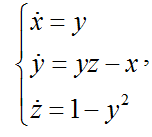
MATLABのノーズフーバーモデル：

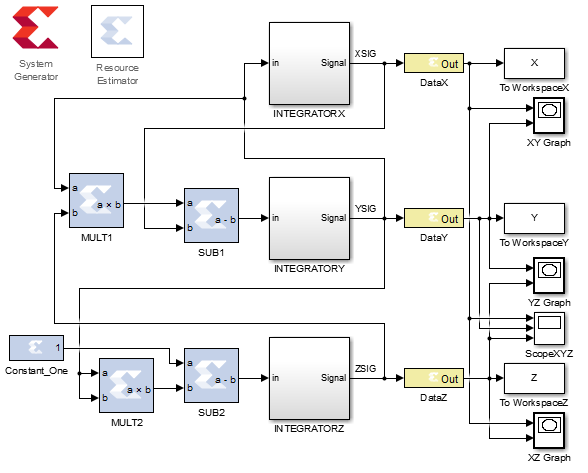
一時的な実装：

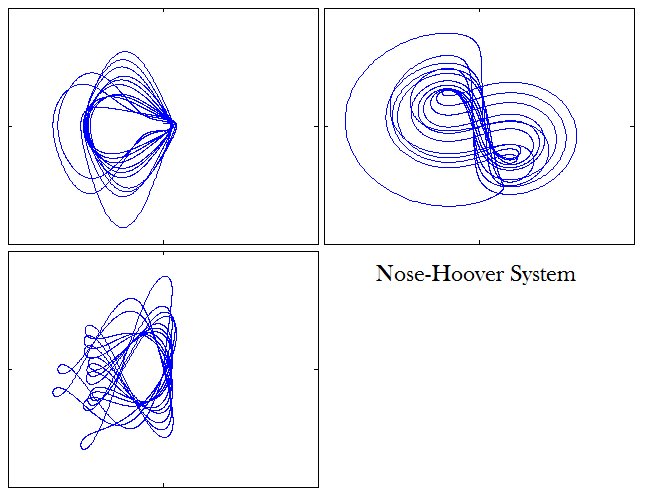
アトラクタの2次元投影：

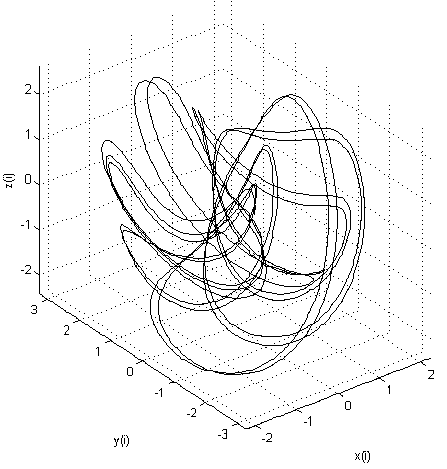
Nose-Hooverサーモスタットの3次元モデル：

サーモスタット（2番目のバージョン）

プロジェクト合成

プロジェクトを合成するには、赤い「X」アイコンをクリックしてSystem Generatorの設定を起動する必要があります。ここで、FPGAのファミリとタイプ、結果のファイル形式（VHDL / Verilog-ソースコードを作成、NGC-接続のリストとしてカーネルを作成）、クロック周波数の予備値などを選択できます。私の典型的な設定を次の図に示します。

すべての設定を設定した後、「生成」をクリックすると、出力にFPGAの合成プロジェクトが作成されます。次に、生成されたカーネルを必要なプロジェクトの部分に挿入するのはあなた次第です。（これを行う方法については、デジタル信号処理に関する他の記事をご覧ください）。これらのアトラクタはすべて、最新のFPGAのリソースをほとんど占有しません（約10〜20個のDSP48ブロックと少しのロジック）。

人生の例

オシロスコープ画面上のローレンツアトラクタ：

ローレンツアトラクタに似た銀河系：

おわりに

リストされたアトラクタは、物理学、化学から力学、気象学まで、科学技術のさまざまな分野の多くの物理プロセスで使用されています。特に、カオスジェネレータは、擬似乱数（PSP）の長いシーケンスを作成するために使用されます。無線工学の問題では、デジタル手法（FPGAまたはプロセッサ上）を使用して超広帯域信号を作成するときに、カオスを使用してキャリアを変調できます。

カオス理論は興味深く驚くべき科学です。そして、分析とモデリングの最新の手段のおかげで、研究にとって非常に魅力的になります。この記事の助けを借りて、3を超える次数の超カオスシステム（たとえば、Lorentz、Rosslerなどのハイパーカオス）まで、独自の動的システムを独立してモデリングできます。私の出版物の資料が誰かにとって役に立つかもしれないが、誰かが自分にとって新しくて役に立つものを見つけることを願っています。

Github Attractorソースファイル

同様のトピックに関する私の記事：

文学

^{万歳、FPGAハブがハブに戻った} ^{明けましておめでとうございます！}

FPGAカオスジェネレーター