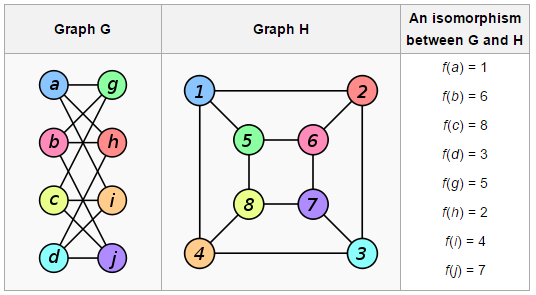
これらの2つのグラフは同型です。
シカゴ大学のコンピュータサイエンスおよび数学学部の数学者LászlóBabaiは、計算の複雑さの理論における基本的な問題の1つであるグラフ同型問題を解くための高速で新しいアルゴリズムを導入しました。 このアルゴリズムは、問題をクラスPに非常に近づけます。一部の専門家によると 、これは、数十年ではないとしても、10年で理論計算機科学の最も重要な結果の1つです。
Laszlo は、 1か月前にアルゴリズムの作成を発表しました 。 彼によると、このアルゴリズムは、30年以上にわたって記録保持者であった既存のアルゴリズムよりもはるかに効果的です。1983年にEugene Lux教授によって開発され、指数関数的ではない時間で問題を解決しました。
Laszlo Babayは、明らかに、問題をクラスPの問題に実際に減らすことができました。彼のアルゴリズムは、準多項式時間で計算されていると宣言されています。
2015年12月11日、新しいアルゴリズムを説明する記事がようやくパブリックドメインで公開され、コンピュータエンジニアリング協会にも送られました。 アルゴリズムの公式発表は、 第48回計算理論シンポジウムで行われます。
数十年間、グラフ同型の問題は、計算の複雑さの理論において特別な地位にありました。 他の何百もの問題がクラスPまたはクラスNPによる分類に謙虚に屈した一方で、グラフ同型の問題は明確に分類できませんでした。 簡単なタスクよりも複雑で、複雑なタスクよりも簡単で、2つのクラスの問題の間にあるかのようにユニークな位置を占めていました。 マサチューセッツ工科大学の数学者であるスコットアーロンソンは、これはこの奇妙な中間領域における2つの有名な課題の1つです。 今、彼は言った、「2人のうち1人が降伏したようだ」。
灰色の領域でよく知られている2番目の問題は、整数の因数分解です。
グラフの同型の問題自体は単純に見えます。2つのグラフが同型かどうかを判断する必要があります。つまり、頂点間の接続を維持しながら、頂点を移動するだけでグラフを別のグラフに変換できます。 以上です。 見かけの単純さにもかかわらず、小さなグラフでもさまざまな形をとることがあるため、この問題を解決するのは困難です。

Laszlo Babaiは、2015年11月10日にシカゴ大学でグラフ同型問題を解くためのアルゴリズムを発表します
Laszlo Babayaアルゴリズムは、グラフの頂点を仮想的に「着色」することにより機能します。 最初に、いくつかの頂点がランダムに選択され、異なる色で「ペイント」されます。 次に、おそらく最初のグラフの頂点に対応するいくつかの頂点が2番目のグラフで選択され、同じ色が割り当てられます。 最後に、すべてのオプションが整理されます。 最初の選択後、アルゴリズムは両方のグラフで、最初に選択された頂点に隣接する推定同型頂点を、頂点間にリンクがなくなるまで異なる色で色付けします。
Babayaアルゴリズムが同僚のテストに合格した場合、これは近年の数学のこのセクションで最も重要な発見です。 サンタフェ研究所のジョシュア・グロチョウは、「彼の発表の前に、おそらく自分自身を除いて、今後10年以内にそのような結果が現れると予想したことはまずありませんでした」と述べた。
過去数週間にわたって、ババイは彼のアルゴリズムの概要を説明するいくつかの講義を行ってきました。 11月10日の最初の講義のビデオを以下に示します。
グラフ同型の問題は「普遍的」であると考えられます。つまり、あらゆる問題をそれに還元することができ、組み合わせ構造の同型の問題が提起されます。 通常、この「汎用性」はクラスNPの問題の特徴です。 同時に、グラフ同型問題は、NP完全問題にはない奇妙な特性を示しました。「ブラインドテスト」に合格すること( Arthur-Merlinプロトコル )。
2012年に、理論情報学の分野の科学者を対象とした非公式の調査で次の結果が得られました。そのうち14人はグラフ同型の問題はクラスPに属し、6人はそうではないと述べました。 Laszlo Babaiが発表される前は、近い将来問題が解決されるとは考えていませんでした。 「多分クラスPに属しているのかそうでないのかと思ったが、私の生涯に誰もこれを知らないだろう」とGrochowは認めた。
Laszlo Babaiは、ほぼ40年間グラフ同型の問題に取り組んできました。