新しいvw-hyperoptモジュールによるVowpal Wabbitのハイパーパラメーターの最適化

こんにちは、Habr！ この記事では、ハイパーパラメーターの最適化など、機械学習のあまり好ましくない側面に焦点を当てます。 2週間前、 vw-hyperopt.pyモジュールは、非常に有名で有用なVowpal Wabbit プロジェクトに投入され ました 。このプロジェクトでは、大規模な空間でVowpal Wabbitモデルのハイパーパラメーターの適切な構成を見つけることができます。 このモジュールは、DCA（Data-Centric Alliance）によって内部的に開発されました。









適切な構成を見つけるために、vw-hyperoptはHyperopt Pythonライブラリのアルゴリズムを使用し、Tree-Structured Parzen Estimators（TPE）メソッドを使用してハイパーパラメーターを適応的に最適化できます。 これにより、反復回数が等しい単純なグリッド検索よりも優れた最適化を見つけることができます。



この記事は、Vowpal Wabbitを扱うすべての人、特に、ソースコードで多数のモデルノブを構成する方法がなく、手動で調整するか、最適化自体をエンコードする方法がないことに悩んでいる人にとって興味深いものです。

ハイパーパラメーター

ハイパーパラメーターとは何ですか？ これらはすべてアルゴリズムの「自由度」であり、直接最適化されませんが、結果に依存します。 結果がかなり異なる場合があり、それがカグルでない場合は、デフォルト値を使用するか、手動で選択できます。 ただし、設定が失敗するとすべてが台無しになる場合があります。アルゴリズムは再訓練を行うか、逆にほとんどの情報を使用できなくなります。



狭い意味では、ハイパーパラメーターは、多くの場合、機械学習方法の正則化およびその他の「明らかな」設定のみを意味します。 ただし、広い意味で、ハイパーパラメーターは一般に、結果に影響を与える可能性のあるデータを使用した操作です：エンジニアリング機能、観測値の重み付け、アンダーサンプリングなど。

グリッド検索

もちろん、パラメーターの最適化に加えて、ハイパーパラメーターも最適化するアルゴリズムを用意しておくといいでしょう。 直感よりもこのアルゴリズムを信頼できればなおさらです。 もちろん、この方向にいくつかのステップが取られています。 素朴な方法は多くの機械学習ライブラリに組み込まれています：グリッド検索-グリッドを歩く、またはランダム検索-固定分布からのサンプリングポイント（最も有名なインスタンスは、sklearnのGridSearchCVとRandomizedGridSearchCVです）。 グリッドパスの利点は、独自にコーディングしやすく、並列化が簡単なことです。 ただし、これには重大な欠点もあります。

• 彼は明らかに失敗した多くのポイントを調べます。 結果またはその他の情報を含むいくつかの構成セットが既にあるとします。 人は、どの構成が間違いなくずさんな結果をもたらすかを理解でき、これらの領域を再度チェックしないように推測します。 グリッド検索はこれを行う方法を知りません。
  
  
  
  
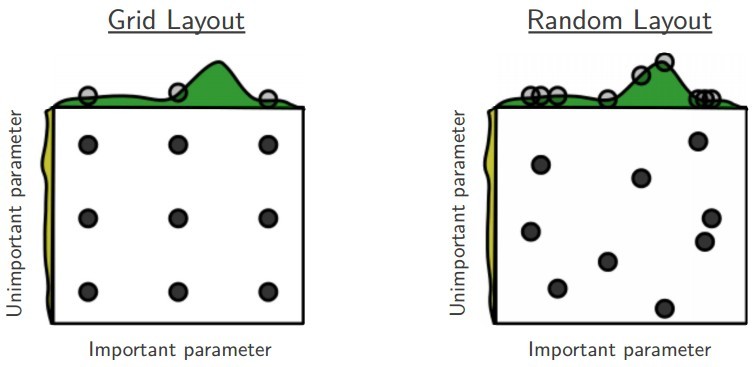
• ハイパーパラメータが多数ある場合、「セル」のサイズを大きくしすぎる必要があり、適切な最適化を見逃す可能性があります。 したがって、結果に影響を与えない多くの余分なハイパーパラメーターを検索スペースに含めると、同じ数の反復でグリッド検索が非常に悪くなります。 ただし、ランダム検索の場合、これはそれほどではありません。
  
  

ベイジアン法

反復回数を減らして適切な構成を見つけるために、適応型ベイジアン手法が考案されました。 彼らは、チェック済みのポイントの結果を考慮して、チェックする次のポイントを選択します。 アイデアは、（a）見つかったポイントの中で最も成功したポイントの近くの領域を探索し、（b）さらに成功したポイントが配置される可能性のある不確実性の高い領域を探索する間の各ステップで妥協点を見つけることです。 これは、探索エクスプロイトまたはラーニングvs獲得ジレンマと呼ばれることがよくあります。 したがって、新しい各ポイントのチェックに費用がかかる状況（機械学習、検証=学習+検証）では、はるかに少ないステップでグローバル最適にアプローチできます。



さまざまなバリエーションの同様のアルゴリズムが、 MOE 、 Spearmint 、 SMAC 、 BayesOpt 、およびHyperoptツールに実装されています 。 vw-hyperopt



はvw-hyperopt



のラッパーであるため、後者について詳しく説明しますが、最初にVowpal Wabbitについて少し説明する必要があります。

ヴォーパルウサギ

あなたの多くは、このツールを使用したか、少なくとも聞いたことがあるはずです。 要するに、それは世界の機械学習ライブラリで最速の（最速でないとしても）の1つです。 CTR予測子（バイナリ分類）のモデルを3,000万のケースと数千万の機能でトレーニングするには、1コアで数ギガバイトのRAMと6分しかかかりません。 Vowpal Wabbitは、いくつかのオンラインアルゴリズムを実装しています。

• さまざまな機能を備えた確率的勾配降下;
• FTRL-Proximal、 ここで読むことができます ;
• SVMのオンライン類似性;
• オンラインブースティング;
• 因数分解マシン。

さらに、フィードフォワードニューラルネットワーク、バッチ最適化（BFGS）およびLDAを実装しています。 バックグラウンドでVowpal Wabbitを実行し、それらから学習するか、単に予測を行うことで、入力としてデータストリームを受信できます。



FTRLとSGDは、回帰と分類の両方の問題を解決できます。これは、損失関数によってのみ規制されます。 これらのアルゴリズムは、特徴に関して線形ですが、多項式の特徴を使用して非線形性を簡単に実現できます。 あまりにも多くの時代を示している場合、再訓練から身を守るための非常に便利な早期停止メカニズムがあります。



Vowpal Wabbitは、その機能ハッシングでも有名です。これは、多くの機能がある場合に追加の正則化として機能します。 これにより、数十億の希少なカテゴリを持つカテゴリ機能を学習し、品質を犠牲にすることなくモデルをRAMに適合させることができます。



Vowpal Wabbitには特別な入力データ形式が必要ですが 、理解するのは簡単です。 それは自然にまばらで、ほとんどスペースを取りません。 一度に1つの観測（またはLDAの場合は複数）がRAMにロードされます。 トレーニングは、コンソールから実行するのが最も簡単です。



興味のある方は、 チュートリアル 、リポジトリ内のその他の例、記事、およびプレゼンテーションを読むことができます。 Vowpal Wabbitの内部については、John Langfordの出版物と彼のブログで詳しく知ることができます。 Habréにも適切な投稿があります。 引数のリストは、 vw --help



からvw --help



か、 詳細な説明を読むことができます。 説明からわかるように、多数の引数があり、それらの多くは最適化できるハイパーパラメーターと見なすことができます。



Vowpal Wabbitには、黄金 比 法を使用して 1つのハイパーパラメーターを選択できるvw-hypersearchモジュールがあります。 ただし、いくつかの極小値がある場合、この方法は最良の選択肢からは程遠いものになる可能性があります。 さらに、多くのハイパーパラメーターを一度に最適化する必要がありますが、vw-hypersearchではそうではありません。 数ヶ月前、多次元ゴールデンセクションメソッドを記述しようとしましたが、収束に必要なステップ数がグリッド検索を超えていたため、このオプションは不要になりました。 Hyperoptを使用することが決定されました。

ハイパーオプト

このPythonライブラリは、Tree-Structured Parzen Estimators（TPE）最適化アルゴリズムを実装しています。 その利点は、非常に「厄介な」スペースで動作できることです。1つのハイパーパラメーターが連続している場合、もう1つはカテゴリー型です。 3番目は離散的ですが、その隣接値は互いに相関しています。 最後に、パラメータ値のいくつかの組み合わせは単に意味をなさない場合があります。 TPEは、先験的確率を持つ階層検索空間を取り込み、各ステップでそれらを新しい点を中心とするガウス分布と混合します。 著者のJames Bergstraは、このアルゴリズムが探索-悪用の問題を十分に解決し、グリッド検索とエキスパート検索の両方、少なくとも多くのハイパーパラメータが存在するディープラーニングタスクの両方でうまく機能すると主張しています。 詳細については、 こちらとこちらをご覧ください 。 TPEアルゴリズムについては、 こちらをご覧ください 。 おそらく将来、彼についての詳細な記事を書くことが可能になるでしょう。



Hyperoptは、よく知られた機械学習ライブラリのソースコードに埋め込まれていませんでしたが、多くはそれを使用しています。 たとえば、これはhyperopt + sklearnに関する優れたチュートリアルです 。 hyperopt + xgboostのアプリケーションを次に示します。 私の貢献はすべて、Vowpal Wabbitのこのようなラッパー、サーチスペースを指定し、コマンドラインからこれらすべてを起動するための多かれ少なかれ許容できる構文です。 Vowpal Wabbitはまだそのような機能を持っていなかったので、Langfordは私のモジュールを気に入ってそれを注ぎました。 実際、誰でもお気に入りの機械学習ツールにHyperoptを試すことができます。これは簡単に実行でき、必要なものはすべてこのチュートリアルにあります。

vw-hyperopt

vw-hyperopt



使用にvw-hyperopt



ましょう。 まず、githubからVowpal Wabbitの最新バージョンをインストールする必要があります。 モジュールはutlフォルダーにあります。



注意！ これまでの最新の変更（特に、新しいコマンド構文）（12月15日）は、メインリポジトリにマージされません。 数日中に、問題が解決することを願っていますが、今のところ、私のブランチの最新バージョンのコードを使用できます。 編集： 12月22日、変更が注ぎ込まれ、メインリポジトリを使用できるようになりました。

使用例：

 ./vw-hyperopt.py --train ./train_set.vw --holdout ./holdout_set.vw --max_evals 200 --outer_loss_function logistic --vw_space '--algorithms=ftrl,sgd --l2=1e-8..1e-1~LO --l1=1e-8..1e-1~LO -l=0.01..10~L --power_t=0.01..1 --ftrl_alpha=5e-5..8e-1~L --ftrl_beta=0.01..1 --passes=1..10~I --loss_function=logistic -q=SE+SZ+DR,SE~O --ignore=T~O' --plot
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このモジュールには、トレーニングと検証のサンプル、および--vw_space



事前分布（ --vw_space



内で引用）が必要です。 整数、連続、またはカテゴリーのハイパーパラメーターを指定できます。 カテゴリーを除くすべてについて、均一分布または対数均一分布を指定できます。 この例の検索スペースは、 vw-hyperopt



内でvw-hyperopt



次のように変換されます（ Hyperopt



チュートリアルをHyperopt



だ場合、これを理解できます）。

 from hyperopt import hp prior_search_space = hp.choice('algorithm', [ {'type': 'sgd', '--l1': hp.choice('sgd_l1_outer', ['empty', hp.loguniform('sgd_l1', log(1e-8), log(1e-1))]), '--l2': hp.choice('sgd_l2_outer', ['empty', hp.loguniform('sgd_l2', log(1e-8), log(1e-1))]), '-l': hp.loguniform('sgd_l', log(0.01), log(10)), '--power_t': hp.uniform('sgd_power_t', 0.01, 1), '-q': hp.choice('sgd_q_outer', ['emtpy', hp.choice('sgd_q', ['-q SE -q SZ -q DR', '-q SE'])]), '--loss_function': hp.choice('sgd_loss', ['logistic']), '--passes': hp.quniform('sgd_passes', 1, 10, 1), }, {'type': 'ftrl', '--l1': hp.choice('ftrl_l1_outer', ['emtpy', hp.loguniform('ftrl_l1', log(1e-8), log(1e-1))]), '--l2': hp.choice('ftrl_l2_outer', ['emtpy', hp.loguniform('ftrl_l2', log(1e-8), log(1e-1))]), '-l': hp.loguniform('ftrl_l', log(0.01), log(10)), '--power_t': hp.uniform('ftrl_power_t', 0.01, 1), '-q': hp.choice('ftrl_q_outer', ['emtpy', hp.choice('ftrl_q', ['-q SE -q SZ -q DR', '-q SE'])]), '--loss_function': hp.choice('ftrl_loss', ['logistic']), '--passes': hp.quniform('ftrl_passes', 1, 10, 1), '--ftrl_alpha': hp.loguniform('ftrl_alpha', 5e-5, 8e-1), '--ftrl_beta': hp.uniform('ftrl_beta', 0.01, 1.) } ])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

オプションで、検証サンプルの損失関数と反復の最大数を変更できます（デフォルトでは--max_evals



、デフォルトでは--max_evals



、デフォルトでは100）。 matplotlib



と、できればseaborn



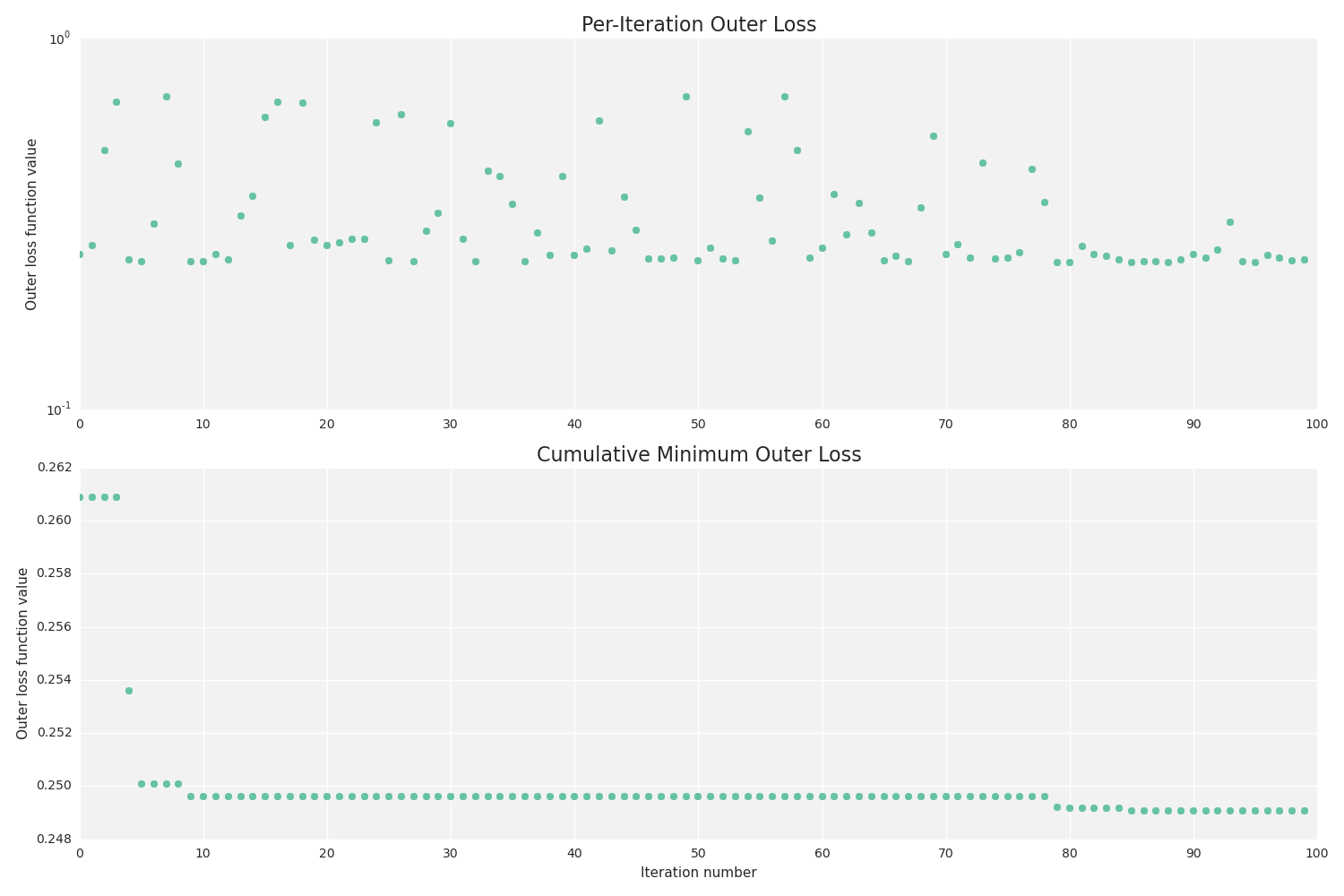
場合は、各反復の結果を保存し、-- --plot



グラフを作成することもできます。

ドキュメント

ハブに詳細なドキュメントを配置することは慣習ではないため、リンクへのリンクに限定します。 私のフォークでロシア語ウィキのすべてのセマンティクスについて読むか、メインのVowpal Wabbitリポジトリで英語版を待つことができます。

計画

将来的には、モジュールに追加する予定です。

1. 回帰およびマルチクラス分類タスクのサポート。
   
   
   
   
2. 「ウォームスタート」のサポート：事前に評価されたHyperoptポイントを発行し、それらの結果を考慮して最適化を開始します。
   
   
   
   
3. 別のテストサンプルの各ステップでエラーを評価するオプション（ただし、ハイパーパラメーターを最適化しない）。 これは、一般化能力をよりよく評価するために必要です-再訓練していません。
   
   
   
   
4. --lrqdropout, --normalized, --adaptive
   
   
   
   など、値を受け入れないバイナリパラメータのサポート これで、原則として--adaptive=\ ~O
   
   
   
   記述できますが、これはまったく直感的ではありません。 --adaptive=~B



--adaptive=~BO
   
   
   
   または--adaptive=~BO
   
   
   
   ようなことができます。

誰かがモジュールを使用し、彼が誰かを助けてくれたらとてもうれしいです。 提案、アイデア、または発見されたバグに喜んで対応します。 ここにそれらを書くか、githubで問題を作成できます。

アップデート12.22.2015

最新の変更を含むプルリクエストがメインのVowpal Wabbitリポジトリに追加されたため、ブランチではなく使用できるようになりました。