コードをすぐに提供してください!
import numpy as np X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ]) y = np.array([[0,1,1,0]]).T alpha,hidden_dim = (0.5,4) synapse_0 = 2*np.random.random((3,hidden_dim)) - 1 synapse_1 = 2*np.random.random((hidden_dim,1)) - 1 for j in xrange(60000): layer_1 = 1/(1+np.exp(-(np.dot(X,synapse_0)))) layer_2 = 1/(1+np.exp(-(np.dot(layer_1,synapse_1)))) layer_2_delta = (layer_2 - y)*(layer_2*(1-layer_2)) layer_1_delta = layer_2_delta.dot(synapse_1.T) * (layer_1 * (1-layer_1)) synapse_1 -= (alpha * layer_1.T.dot(layer_2_delta)) synapse_0 -= (alpha * XTdot(layer_1_delta))
パート1:最適化
最初の部分では、単純なニューラルネットワークでの逆伝播の基本原理について説明しました。 ネットワークにより、各ネットワークの重みがエラーにどのように寄与するかを測定できました。 そしてこれにより、別のアルゴリズムである勾配降下法を使用して重みを変更できました。
何が起こっているかの本質は、逆伝播はネットワークに最適化を導入しないということです。 ネットワークの端から内部のすべての重みに誤った情報を移動するため、別のアルゴリズムがすでにこれらの重みを最適化してデータに一致させることができます。 しかし、原則として、逆伝播で使用できる非線形最適化の他の方法が豊富にあります。
いくつかの最適化方法:
差異の視覚化:
さまざまな方法がさまざまなケースに適しており、場合によっては組み合わせることもできます。 このレッスンでは、勾配降下を検討します。これは、最も単純で最も一般的なニューラルネットワーク最適化アルゴリズムの1つです。 したがって、設定とパラメーター化によりニューラルネットワークを改善します。
パート2:勾配降下
丸いバスケットに赤いボールがあるとしましょう(下の写真)。 ボールは底を見つけようとしています。 これは最適化です。 この例では、ボールはバケット内の最低点を探して、左から右にその位置を最適化します。
ボールには、左または右の2つの移動オプションがあります。 目標は、可能な限り低い位置を取ることです。 キーボードからボールを制御する場合は、ボタンを左右に押す必要があります。
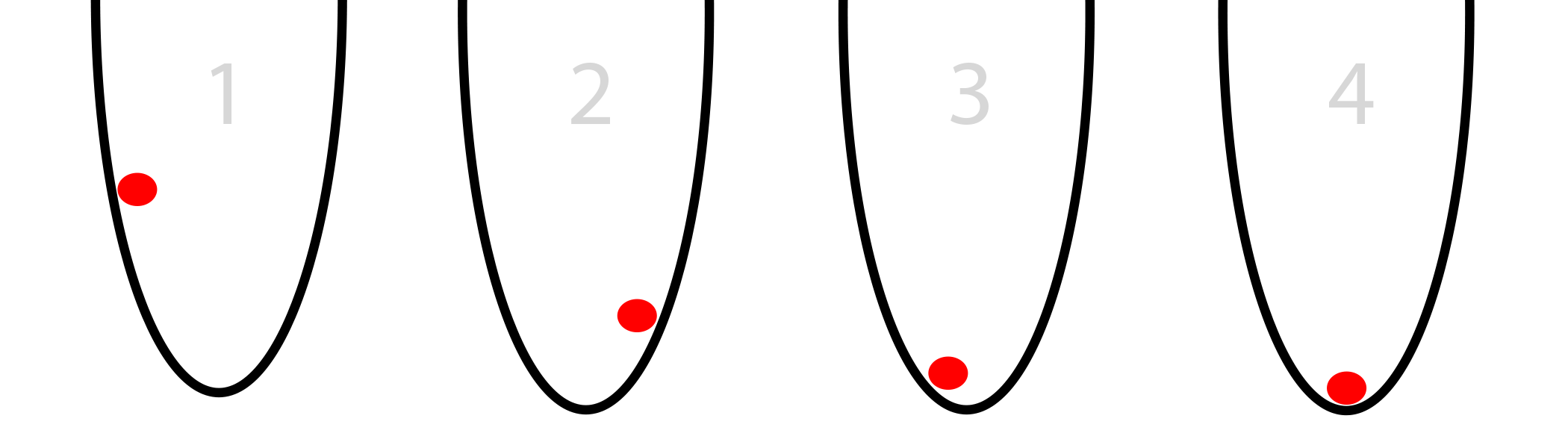
この場合、ボールは、現在の位置(壁に接している、青で表示)でのバケットの側面の勾配のみを認識しています。 傾きが負の場合、ボールは右に移動する必要があることに注意してください。 正の場合-左側。 明らかに、この情報は数回の繰り返しでバケットの底を見つけるのに十分です。 この種の最適化は、勾配最適化と呼ばれます。
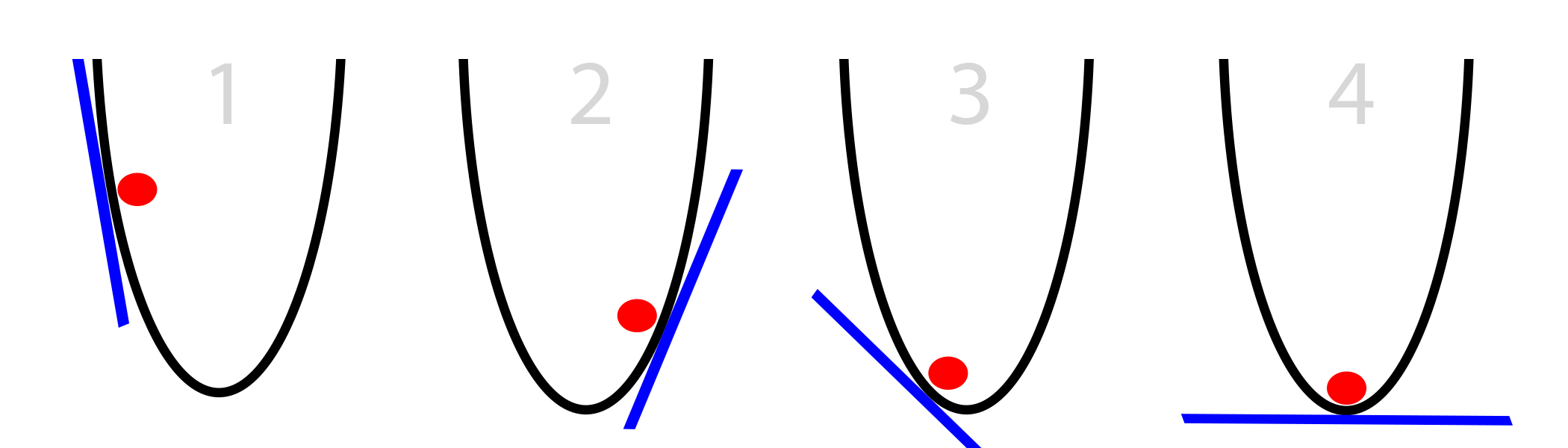
HSの最も単純なケース:
- 私たちのポイントで勾配を計算する
- 負の場合、右に移動します
- 正の場合、左に移動します
- 勾配が0になるまで繰り返します
問題は、各ステップでボールがどれだけ動くかです。 写真は、下から遠くなるほど、勾配が急になることを示しています。 この知識を使用してアルゴリズムを改善します。 また、バケットは平面(x、y)上にあると仮定します。 したがって、ボールの位置はx座標によって決まります。 xを大きくすると、ボールが右に移動します。
最も単純な勾配降下法:
- 現在の位置xでの勾配の勾配をカウントする
- xを勾配で減少(x = x-勾配)
- 勾配が0になるまで繰り返します
このアルゴリズムは既に少し最適化されています。これは、大きな勾配の場合は大幅なシフトを行い、小さな勾配の場合は小さなシフトを行うためです。 その結果、バスケットの底に近づくと、ボールは傾きがゼロのポイントに到達するまで、すべての減少する変動を行います。 これが収束点になります。
パート3:時々うまくいかない
勾配降下は不完全です。 彼の問題と人々がそれらをどうやって回避するかを考えてください。
問題1:勾配が大きすぎる
私たちのステップは、斜面の大きさに依存します。 大きすぎる場合、必要なポイントを飛び越えることができます。 あまり激しくジャンプしなくても怖くない。 しかし、あなたはそれを非常にジャンプすることができるので、以前よりもさらに遠くなるでしょう。
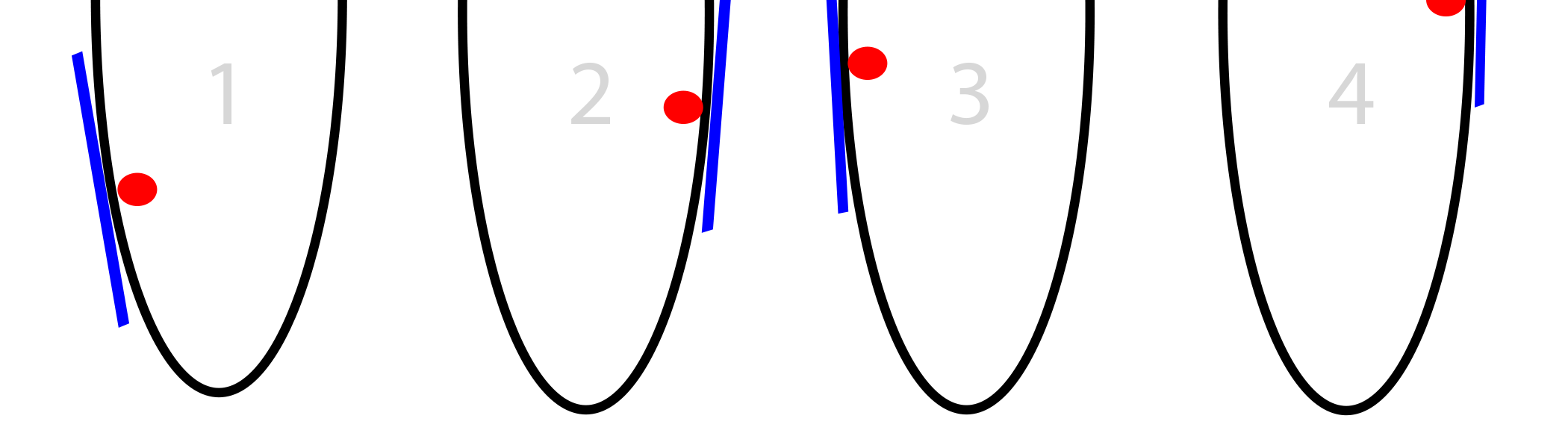
そして、すでにそこに、私たちはもちろん、より大きなバイアスを見つけ、さらにジャンプし、分岐を取得します。
解決策1:バイアスを減らす
0から1の数字(たとえば、0.01)で乗算します。 この定数をアルファと呼びましょう。 そのような削減の後、ネットワークは収束します。これは、目的のポイントにそれほどジャンプしないためです。

勾配降下の改善:
alpha = 0.1(または0〜1の任意の数)
- 現在のx位置の勾配をカウントする
- x = x-(アルファ*勾配)
- (勾配== 0まで繰り返す)
問題2:ローカル低
時々、バケツは非常にcな形をしており、斜面をたどるだけでは絶対的な最小値にならないことがあります。
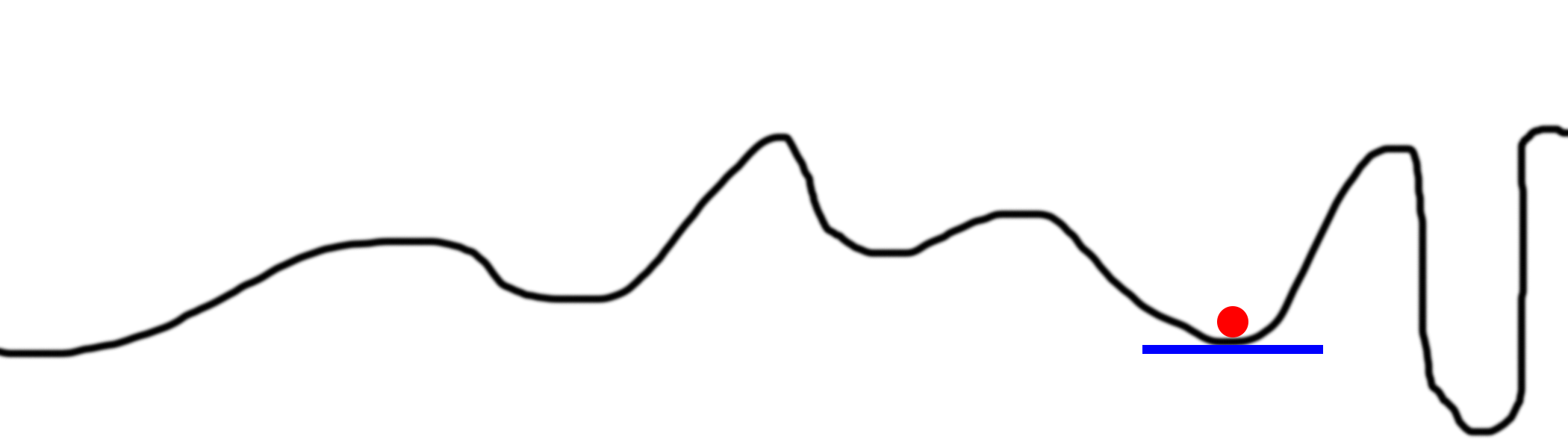
これが最も難しい勾配降下問題です。 それを回避する方法はたくさんあります。 通常、彼らはバケットのさまざまな部分を試し、ランダム検索を使用します。
解決策2:複数のランダムな開始点
さて、しかし、グローバル最小値を見つけるためにランダム性を使用する場合、なぜ最適化を行う必要があるのでしょうか? ランダムに解決策を模索するでしょうか?
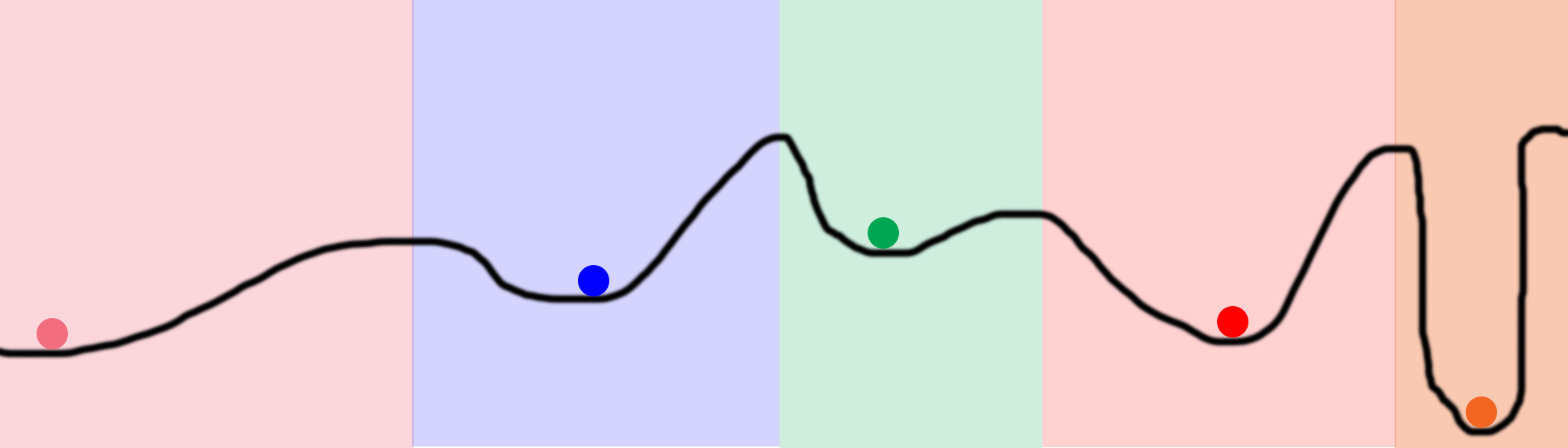
このチャートを検討してください。 ラインに100の目標を設定し、それらの最適化を開始したとしましょう。 その結果、それらは色付きの円でマークされた5つの位置になります。 色付きの領域は、各ローカルミニマムの所有権を示します。 たとえば、ボールが青い領域に落ちた場合、青い最小値になります。 つまり、空間全体を探索するために、ランダムに5箇所だけを見つける必要があります。 これは、行のすべての場所を試行する完全にランダムな検索よりもはるかに優れています。
ニューラルネットワークに関しては、これは非常に大きな隠れレベルを設定することで実現できます。 レベル内の各非表示ノードは、ランダムな状態で動作を開始します。 次に、各ノードは何らかの最終状態に収束します。 そのサイズにより、ネットワークユーザーは同じネットワーク上で数千または数百万の異なるローカルミニマムを試すことができます。
注1:これらはニューラルネットワークであり、有益です。 スペース全体を計算することなく、スペースを検索する機会があります。 5つのボールと少数の反復を使用して、上の図の黒い線全体を検索できます。 ブルートフォース検索では、数桁のプロセッサー能力が必要になります。
注2:好奇心reader盛な読者は、「なぜ、多数の異なるノードを同じポイントに収束させるべきなのでしょうか?」と尋ねます。 これは計算能力の無駄です!」 いい質問です。 隠されたノードを回避するアプローチもあります-これらはドロップアウトとドロップ接続です。これについては後で説明します。
問題3:勾配が小さすぎる
斜面は時々小さすぎます。 そのようなスケジュールを検討してください。

ボールが詰まっています。 これは、アルファが小さすぎる場合に発生します。 彼はすぐに局所的な最小値を見つけ、他のすべてを無視します。 そして、もちろん、このような小さな動きでは、収束には非常に長い時間がかかります。

解決策3:アルファを増やす
明らかに、アルファを増やすことができ、デルタに1より大きい数値を掛けることさえできます。これはめったに使用されませんが、実際に起こります。
パート4:ニューラルネットワークの確率的勾配降下
では、これらのボールとラインは、ニューラルネットワークと逆伝播にどのように関係していますか? このトピックは複雑であると同時に重要です。

ニューラルネットワークでは、重みに関するエラーを最小限に抑えようとします。 この線は、スケールの1つの位置に関するネットワークエラーを表します。 重みのいずれかの可能な値のネットワークエラーを計算した場合、結果はそのような線で表されます。 次に、最小誤差(曲線の最低部分)に対応する重み値を選択します。 グラフは2次元なので、1つの重みを言います。 xは重み値、yは重みがxの値に含まれる瞬間のニューラルネットワークのエラーです。
では、このプロセスが単純な2レベルのニューラルネットワークでどのように機能するかを見てみましょう。
import numpy as np # def sigmoid(x): output = 1/(1+np.exp(-x)) return output # def sigmoid_output_to_derivative(output): return output*(1-output) # X = np.array([ [0,1], [0,1], [1,0], [1,0] ]) # y = np.array([[0,0,1,1]]).T # np.random.seed(1) # 0 synapse_0 = 2*np.random.random((2,1)) - 1 for iter in xrange(10000): # layer_0 = X layer_1 = sigmoid(np.dot(layer_0,synapse_0)) # ? layer_1_error = layer_1 - y # # l1 layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1) synapse_0_derivative = np.dot(layer_0.T,layer_1_delta) # synapse_0 -= synapse_0_derivative print " :" print layer_1
この例では、出力に1行のエラーがあり、35行目でカウントされます(layer_1_error = layer_1-y)。 2つの重みがあるため、エラーのあるチャートは3次元空間に配置されます。 これはスペース(x、y、z)になり、エラーが垂直に移動します。xとyはsyn0の重みの値です。
データセットのエラーサーフェスを描画してみましょう。 特定の重みセットの誤差をどのように計算しますか? このカウントは、行31、32、および35にあります。
layer_0 = X layer_1 = sigmoid(np.dot(layer_0,synapse_0)) layer_1_error = layer_1 - y
重みのセットに対して一般的なエラー(xおよびyの場合は-10〜10)を描画すると、次のようになります。
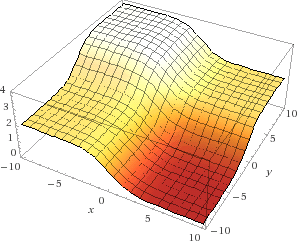
実際、すべてが単純です-可能なすべての重みの組み合わせと、各セットでネットワークによって生成されたエラーを計算します。 xはsynapse_0の最初の重みであり、yはsynapse_0の2番目の重みです。 zはエラーです。 ご覧のとおり、出力は最初の入力セットと正の相関があります。 したがって、xが大きい場合、エラーは最小になります。 どう? いつ最適ですか?
2層ネットワークはどのように最適化されていますか?
そのため、示された3行でエラーをカウントする場合、次はネットワークを最適化してエラーを減らします。 これは、勾配降下が発生する場所です。
layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1) synapse_0_derivative = np.dot(layer_0.T,layer_1_delta) synapse_0 -= synapse_0_derivative
擬似コードを思い出してください:
- 現在の位置xでの勾配の勾配をカウントする
- xを勾配で減少(x = x-勾配)
- 勾配が0になるまで繰り返します
これだ。 変更は、1つの重みではなく2つの重みを最適化することだけです。 論理は同じです。
パート5:ニューラルネットワークの改善
改善1:アルファの追加とカスタマイズ
アルファとは? 前述のように、このオプションは各反復更新のサイズを縮小します。 最後の時点で、重みを更新する前に、更新サイズにアルファ(通常は0〜1)を掛けます。 そして、このような最小限のコード変更は、彼のトレーニング能力に大きく影響します。
前の記事の3レベルのネットワークに戻り、alphaパラメーターを適切な場所に追加しましょう。 次に、アルファに関するすべてのアイデアを実際のコードに合わせるための実験を行います。
- 現在のx位置の勾配をカウントする
- アルファx = x-(アルファ*勾配)でスケーリングされた勾配でxを減らす
- (勾配== 0まで繰り返す)
import numpy as np alphas = [0.001,0.01,0.1,1,10,100,1000] # def sigmoid(x): output = 1/(1+np.exp(-x)) return output # def sigmoid_output_to_derivative(output): return output*(1-output) X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]]) y = np.array([[0], [1], [1], [0]]) for alpha in alphas: print "\n Alpha:" + str(alpha) np.random.seed(1) # 0 synapse_0 = 2*np.random.random((3,4)) - 1 synapse_1 = 2*np.random.random((4,1)) - 1 for j in xrange(60000): # 0, 1 2 layer_0 = X layer_1 = sigmoid(np.dot(layer_0,synapse_0)) layer_2 = sigmoid(np.dot(layer_1,synapse_1)) # ? layer_2_error = layer_2 - y if (j% 10000) == 0: print " "+str(j)+" :" + str(np.mean(np.abs(layer_2_error))) # ? # ? , layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2) # l1 l2 ( )? layer_1_error = layer_2_delta.dot(synapse_1.T) # l1? # ? , layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1) synapse_1 -= alpha * (layer_1.T.dot(layer_2_delta)) synapse_0 -= alpha * (layer_0.T.dot(layer_1_delta))
alpha:0.001 0 :0.496410031903 10000 :0.495164025493 20000 :0.493596043188 30000 :0.491606358559 40000 :0.489100166544 50000 :0.485977857846 alpha:0.01 0 :0.496410031903 10000 :0.457431074442 20000 :0.359097202563 30000 :0.239358137159 40000 :0.143070659013 50000 :0.0985964298089 alpha:0.1 0 :0.496410031903 10000 :0.0428880170001 20000 :0.0240989942285 30000 :0.0181106521468 40000 :0.0149876162722 50000 :0.0130144905381 alpha:1 0 :0.496410031903 10000 :0.00858452565325 20000 :0.00578945986251 30000 :0.00462917677677 40000 :0.00395876528027 50000 :0.00351012256786 alpha:10 0 :0.496410031903 10000 :0.00312938876301 20000 :0.00214459557985 30000 :0.00172397549956 40000 :0.00147821451229 50000 :0.00131274062834 alpha:100 0 :0.496410031903 10000 :0.125476983855 20000 :0.125330333528 30000 :0.125267728765 40000 :0.12523107366 50000 :0.125206352756 alpha:1000 0 :0.496410031903 10000 :0.5 20000 :0.5 30000 :0.5 40000 :0.5 50000 :0.5
異なるアルファ値からどのような結論を引き出すことができますか?
アルファ= 0.001
非常に低い値では、ネットワークはまったく収束しません。 スケールの更新が小さすぎます。 60,000回の反復後でもほとんど変化はありません。 これが私たちの問題#3:勾配が小さすぎるときです。
アルファ= 0.01
良好な収束。60,000回の繰り返しをスムーズに通過しますが、他の場合ほど目標に近く収束しませんでした。 同じ問題番号3。
アルファ= 0.1
最初は非常に速く歩きましたが、その後は遅くなりました。 これはまだ3番目の問題です。
アルファ= 1
好奇心reader盛な読者は、この場合の収束がアルファがない場合とまったく同じであることに気付くでしょう。 1を掛けます。
アルファ= 10
サプライズ-アルファが1を超えると、結果は10,000人になりました。 そのため、これまでのスケールの更新は小さすぎました。 そのため、ウェイトは正しい方向に移動していましたが、その直前にはウェイトが動きすぎていました。
アルファ= 100
値が大きすぎると逆効果になります。 ネットワークのステップが非常に大きいため、エラーの表面で最低点を見つけることができません。 これが私たちの一番の問題です。 ネットワークはエラーの表面を単に前後にジャンプし、どこにも最小値を見つけません。
アルファ= 1000
減少ではなくエラーの増加が発生し、値0.5で停止します。 これは、問題番号3のより極端なバージョンです。
結果を詳しく見てみましょう
import numpy as np alphas = [0.001,0.01,0.1,1,10,100,1000] # def sigmoid(x): output = 1/(1+np.exp(-x)) return output # def sigmoid_output_to_derivative(output): return output*(1-output) X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]]) y = np.array([[0], [1], [1], [0]]) for alpha in alphas: print "\n alpha:" + str(alpha) np.random.seed(1) # 0 synapse_0 = 2*np.random.random((3,4)) - 1 synapse_1 = 2*np.random.random((4,1)) - 1 prev_synapse_0_weight_update = np.zeros_like(synapse_0) prev_synapse_1_weight_update = np.zeros_like(synapse_1) synapse_0_direction_count = np.zeros_like(synapse_0) synapse_1_direction_count = np.zeros_like(synapse_1) for j in xrange(60000): # 0, 1 2 layer_0 = X layer_1 = sigmoid(np.dot(layer_0,synapse_0)) layer_2 = sigmoid(np.dot(layer_1,synapse_1)) # ? layer_2_error = y - layer_2 if (j% 10000) == 0: print "Error:" + str(np.mean(np.abs(layer_2_error))) # ? # ? , layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2) # l1 l2 ( )? layer_1_error = layer_2_delta.dot(synapse_1.T) # l1? # ? , layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1) synapse_1_weight_update = (layer_1.T.dot(layer_2_delta)) synapse_0_weight_update = (layer_0.T.dot(layer_1_delta)) if(j > 0): synapse_0_direction_count += np.abs(((synapse_0_weight_update > 0)+0) - ((prev_synapse_0_weight_update > 0) + 0)) synapse_1_direction_count += np.abs(((synapse_1_weight_update > 0)+0) - ((prev_synapse_1_weight_update > 0) + 0)) synapse_1 += alpha * synapse_1_weight_update synapse_0 += alpha * synapse_0_weight_update prev_synapse_0_weight_update = synapse_0_weight_update prev_synapse_1_weight_update = synapse_1_weight_update print "Synapse 0" print synapse_0 print "Synapse 0 Update Direction Changes" print synapse_0_direction_count print "Synapse 1" print synapse_1 print "Synapse 1 Update Direction Changes" print synapse_1_direction_count
alpha:0.001 Error:0.496410031903 Error:0.495164025493 Error:0.493596043188 Error:0.491606358559 Error:0.489100166544 Error:0.485977857846 Synapse 0 [[-0.28448441 0.32471214 -1.53496167 -0.47594822] [-0.7550616 -1.04593014 -1.45446052 -0.32606771] [-0.2594825 -0.13487028 -0.29722666 0.40028038]] Synapse 0 Update Direction Changes [[ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 1. 0. 1. 1.]] Synapse 1 [[-0.61957526] [ 0.76414675] [-1.49797046] [ 0.40734574]] Synapse 1 Update Direction Changes [[ 1.] [ 1.] [ 0.] [ 1.]] alpha:0.01 Error:0.496410031903 Error:0.457431074442 Error:0.359097202563 Error:0.239358137159 Error:0.143070659013 Error:0.0985964298089 Synapse 0 [[ 2.39225985 2.56885428 -5.38289334 -3.29231397] [-0.35379718 -4.6509363 -5.67005693 -1.74287864] [-0.15431323 -1.17147894 1.97979367 3.44633281]] Synapse 0 Update Direction Changes [[ 1. 1. 0. 0.] [ 2. 0. 0. 2.] [ 4. 2. 1. 1.]] Synapse 1 [[-3.70045078] [ 4.57578637] [-7.63362462] [ 4.73787613]] Synapse 1 Update Direction Changes [[ 2.] [ 1.] [ 0.] [ 1.]] alpha:0.1 Error:0.496410031903 Error:0.0428880170001 Error:0.0240989942285 Error:0.0181106521468 Error:0.0149876162722 Error:0.0130144905381 Synapse 0 [[ 3.88035459 3.6391263 -5.99509098 -3.8224267 ] [-1.72462557 -5.41496387 -6.30737281 -3.03987763] [ 0.45953952 -1.77301389 2.37235987 5.04309824]] Synapse 0 Update Direction Changes [[ 1. 1. 0. 0.] [ 2. 0. 0. 2.] [ 4. 2. 1. 1.]] Synapse 1 [[-5.72386389] [ 6.15041318] [-9.40272079] [ 6.61461026]] Synapse 1 Update Direction Changes [[ 2.] [ 1.] [ 0.] [ 1.]] alpha:1 Error:0.496410031903 Error:0.00858452565325 Error:0.00578945986251 Error:0.00462917677677 Error:0.00395876528027 Error:0.00351012256786 Synapse 0 [[ 4.6013571 4.17197193 -6.30956245 -4.19745118] [-2.58413484 -5.81447929 -6.60793435 -3.68396123] [ 0.97538679 -2.02685775 2.52949751 5.84371739]] Synapse 0 Update Direction Changes [[ 1. 1. 0. 0.] [ 2. 0. 0. 2.] [ 4. 2. 1. 1.]] Synapse 1 [[ -6.96765763] [ 7.14101949] [-10.31917382] [ 7.86128405]] Synapse 1 Update Direction Changes [[ 2.] [ 1.] [ 0.] [ 1.]] alpha:10 Error:0.496410031903 Error:0.00312938876301 Error:0.00214459557985 Error:0.00172397549956 Error:0.00147821451229 Error:0.00131274062834 Synapse 0 [[ 4.52597806 5.77663165 -7.34266481 -5.29379829] [ 1.66715206 -7.16447274 -7.99779235 -1.81881849] [-4.27032921 -3.35838279 3.44594007 4.88852208]] Synapse 0 Update Direction Changes [[ 7. 19. 2. 6.] [ 7. 2. 0. 22.] [ 19. 26. 9. 17.]] Synapse 1 [[ -8.58485788] [ 10.1786297 ] [-14.87601886] [ 7.57026121]] Synapse 1 Update Direction Changes [[ 22.] [ 15.] [ 4.] [ 15.]] alpha:100 Error:0.496410031903 Error:0.125476983855 Error:0.125330333528 Error:0.125267728765 Error:0.12523107366 Error:0.125206352756 Synapse 0 [[-17.20515374 1.89881432 -16.95533155 -8.23482697] [ 5.70240659 -17.23785161 -9.48052574 -7.92972576] [ -4.18781704 -0.3388181 2.82024759 -8.40059859]] Synapse 0 Update Direction Changes [[ 8. 7. 3. 2.] [ 13. 8. 2. 4.] [ 16. 13. 12. 8.]] Synapse 1 [[ 9.68285369] [ 9.55731916] [-16.0390702 ] [ 6.27326973]] Synapse 1 Update Direction Changes [[ 13.] [ 11.] [ 12.] [ 10.]] alpha:1000 Error:0.496410031903 Error:0.5 Error:0.5 Error:0.5 Error:0.5 Error:0.5 Synapse 0 [[-56.06177241 -4.66409623 -5.65196179 -23.05868769] [ -4.52271708 -4.78184499 -10.88770202 -15.85879101] [-89.56678495 10.81119741 37.02351518 -48.33299795]] Synapse 0 Update Direction Changes [[ 3. 2. 4. 1.] [ 1. 2. 2. 1.] [ 6. 6. 4. 1.]] Synapse 1 [[ 25.16188889] [ -8.68235535] [-116.60053379] [ 11.41582458]] Synapse 1 Update Direction Changes [[ 7.] [ 7.] [ 7.] [ 3.]]
上記のコードでは、微分が方向を変える回数を数えます。 これは、「方向変更の更新」の結論に対応します。 バイアス(微分)が方向を変える場合、ローカルミニマムを超えているため、戻る必要があります。 方向が変わらない場合は、おそらくあまり進んでいません。
私たちが見るもの:
- アルファが浅いとき、導関数はほとんど方向を変えませんでした
- アルファが最適な場合、導関数はしばしば方向を変えます
- アルファが大きい場合、導関数はあまり頻繁に方向を変更しません
- アルファが小さい場合、重みは小さい
- アルファが大きい場合、重みも増加します。
改善2:非表示レベルのサイズのパラメーター化
非表示レベルのサイズを大きくすると、繰り返しごとに収束する検索スペースのサイズが大きくなります。そのようなネットワークとその結論を検討してください。
import numpy as np alphas = [0.001,0.01,0.1,1,10,100,1000] hiddenSize = 32 # def sigmoid(x): output = 1/(1+np.exp(-x)) return output # def sigmoid_output_to_derivative(output): return output*(1-output) X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]]) y = np.array([[0], [1], [1], [0]]) for alpha in alphas: print "\n alpha:" + str(alpha) np.random.seed(1) # randomly initialize our weights with mean 0 synapse_0 = 2*np.random.random((3,hiddenSize)) - 1 synapse_1 = 2*np.random.random((hiddenSize,1)) - 1 for j in xrange(60000): # 0, 1 2 layer_0 = X layer_1 = sigmoid(np.dot(layer_0,synapse_0)) layer_2 = sigmoid(np.dot(layer_1,synapse_1)) # ? layer_2_error = layer_2 - y if (j% 10000) == 0: print " "+str(j)+" :" + str(np.mean(np.abs(layer_2_error))) # ? # ? , layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2) # l1 l2 ( )? layer_1_error = layer_2_delta.dot(synapse_1.T) # l1? # ? , layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1) synapse_1 -= alpha * (layer_1.T.dot(layer_2_delta)) synapse_0 -= alpha * (layer_0.T.dot(layer_1_delta))
alpha:0.001 0 :0.496439922501 10000 :0.491049468129 20000 :0.484976307027 30000 :0.477830678793 40000 :0.46903846539 50000 :0.458029258565 alpha:0.01 0 :0.496439922501 10000 :0.356379061648 20000 :0.146939845465 30000 :0.0880156127416 40000 :0.065147819275 50000 :0.0529658087026 alpha:0.1 0 :0.496439922501 10000 :0.0305404908386 20000 :0.0190638725334 30000 :0.0147643907296 40000 :0.0123892429905 50000 :0.0108421669738 alpha:1 0 :0.496439922501 10000 :0.00736052234249 20000 :0.00497251705039 30000 :0.00396863978159 40000 :0.00338641021983 50000 :0.00299625684932 alpha:10 0 :0.496439922501 10000 :0.00224922117381 20000 :0.00153852153014 30000 :0.00123717718456 40000 :0.00106119569132 50000 :0.000942641990774 alpha:100 0 :0.496439922501 10000 :0.5 20000 :0.5 30000 :0.5 40000 :0.5 50000 :0.5 alpha:1000 0 :0.496439922501 10000 :0.5 20000 :0.5 30000 :0.5 40000 :0.5 50000 :0.5
32個のノードでの最良のエラーは0.0009ですが、4つの非表示ノードでの最良のエラーは0.0013です。これは十分に重要です。データセットを表すために、3つ以上のノードは必要ありません。しかし、より多くのノードがあったため、繰り返しごとに大きなスペースを検索し、収束が速くなりました。私たちの場合、違いはわずかですが、複雑なデータセットを扱う場合、それは非常に重要です。