12個で構成されるネットボックスが90％のケースで310±7グラムを超えないように、製造中にキャンディの質量の最大許容偏差を見つける必要がありました。 分布の法則は正常と見なされます。
答えは、標準偏差が
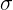生産中のキャンディの質量は超えない 
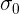= 1.2248、この量は上から制限されていません。
カットの下では、いくつかのモジュロの結果を改善することが期待されますが、それは合理的な仮定です。 以下は十分に厳密に述べられてはいませんが、それでも専門大学のボリュームの数学的分析と確率論の知識が必要です。
箱の質量を正規分布した確率変数にします。 お菓子の質量は、数学的には310/12の期待値で、絶対的に連続したランダム変数の集合体で同じ独立であるとします。 分布密度が数学的期待値に対して対称であり、数学的期待値の右側に増加しないと仮定します（したがって、左側に減少しません）。 お菓子の質量の標準偏差を
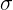そして 
。
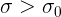キャンディの質量の最大許容偏差以下を推定します
。
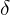お菓子の質量の数学的期待は解に影響しないので、将来は中心のランダム変数で動作します。
明らかに、
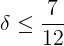必要な条件は確率1で満たされます。以下に、この推定をどのように改善できるかを示します。 
。
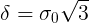fをキャンディの質量分布密度とします。 次に、条件付き確率の定義により、新しい分布密度は次の形式になります。
。
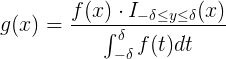この場合、新しいランダム変数には標準偏差が必要です
。
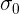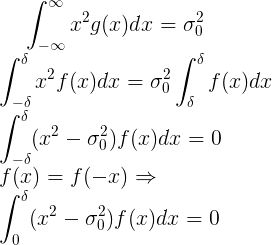
に関して得られた方程式を解決することにより
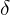既知の分布密度fに必要な推定値を取得します。
さらなる議論のために、補題が必要です。
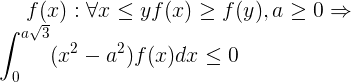
証明：
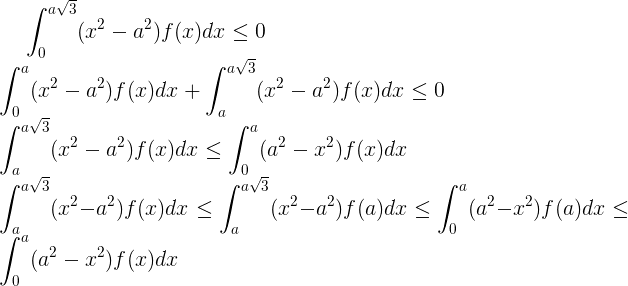
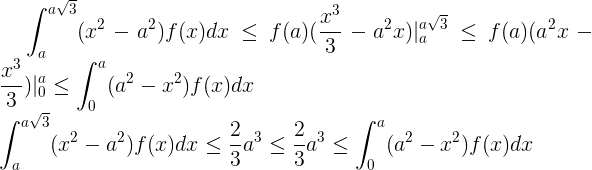
などなど
x<aに対してf(x)>f（a）の正の測定値のセットがある場合、またはa <x <a 3 ^（1/2）の場合f（x）<f（a）の正の測定値のセットがあることに注意してくださいその場合、補題の記述の不平等は厳密になります。
fが数学的な期待値が0の一様確率変数の分布密度である場合、
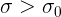それから 。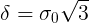
次に、補題を適用すると、お菓子の質量分布が不明であるが、記述されたクラスに属している場合、
。
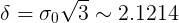他にできること：CLTの適用可能性を評価するには（カイ2乗基準またはBerry – Esseen不等式を介して）、結果の推定値が既知の分布を持つ最適な推定値よりもどれだけ悪いかを見つけます。
最後まで読んでくれた人に感謝します。 数学が大好きです。