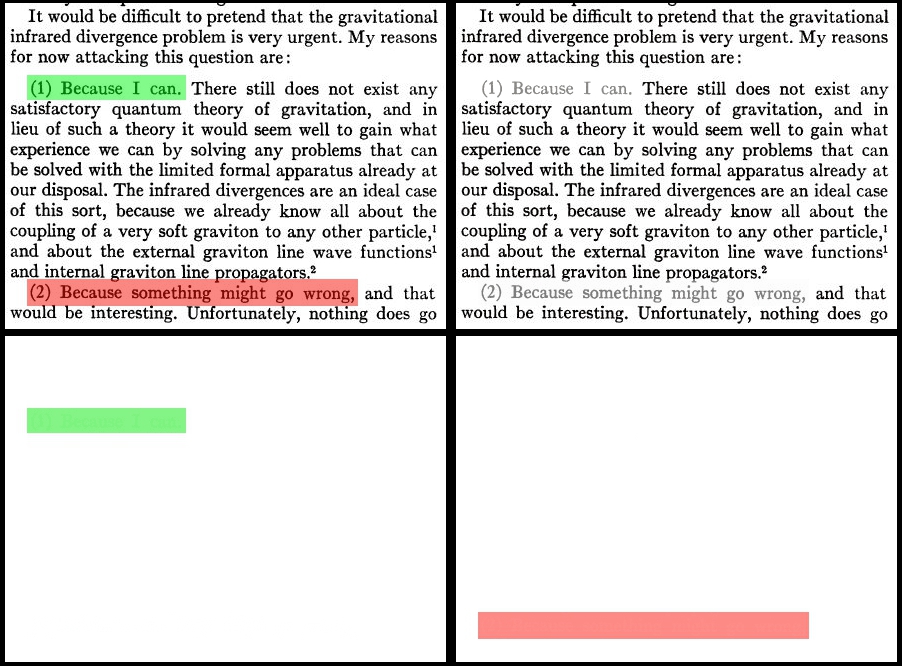
頭に浮かぶ最も単純なアルゴリズムは次のようになります。
- 画像のいくつかの基本的な色を定義します。 これらの色のRGBコンポーネントは、基底ベクトルとして使用されます。
- 各ピクセルの色は、基本的なピクセルの線形結合に分解されます。
- 各基本色の画像を表示します。
- 自尊心は自動的に高まります。
さらに、各アイテムの詳細。
ベースカラー
基本色は、画像セグメントの中間色です。 セグメンテーションアルゴリズム-海が注がれ、味を選択し、一部はMathematicaで実装されています セグメンテーションアルゴリズムの選択にほとんど依存しないことをすぐに言う必要があります。主なことは、クラスターの数がコンポーネントの望ましい数と一致することです。
original = Import["https://hsto.org/files/f42/962/1c5/f429621c55cd46a1beb4d4eb5aefed53.jpg"]; sizeX = First@ImageDimensions[original]; clusters = ClusteringComponents[ original, 3, Method -> "KMeans", DistanceFunction -> CosineDistance ];
必要なもう1つの単純な関数
minIndex
リスト内の最小要素の位置、つまりコンパイルされた置換
Composition[First, Ordering]
返します。
真実のためではなく、真実のために
minIndex = Compile[ { {list, _Real, 1} }, Module[ { i = 0, min = list[[1]], minPos = 1 }, Do[ If[list[[i]] < min, minPos = i; min = list[[i]]], {i, 1, Length@list} ]; minPos ], CompilationTarget -> "C" ];
基底ベクトルを返す関数になりました。
removeDarkest
は最も暗い色を削除します-これは背景なので、必要ありません:
removeDarkest[list_] := Delete[list, minIndex[Norm /@ list]] getBasisColors[image_, clusters_] := Module[ { data = ImageData[image], components = Union[Flatten @ clusters] }, Table[ Median[Join @@ Pick[data, clusters, component]], {component, components} ] ]
起動中...
B1 = removeDarkest@getBasisColors[ColorNegate@original, clusters]
そして出来上がり: 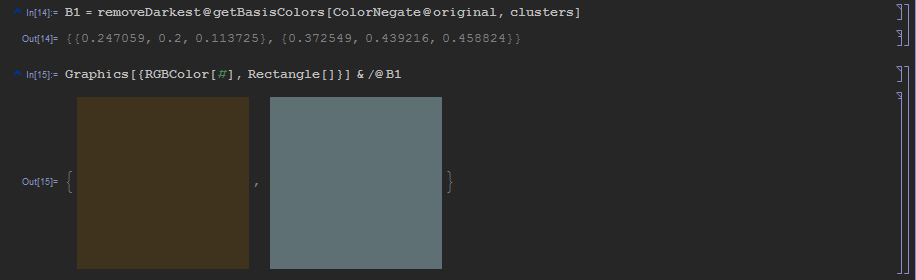
そしていや、ほら、出来上がりじゃない。 画像をこのような基本ベクトルに分解することは意味がありません。結果のコンポーネントは多かれ少なかれクラスターを繰り返します。 ここに真実の瞬間、すなわち 唯一の避けられないヒューリスティックなステップ。 画像のコンポーネントをより完全にするには、基底ベクトルをわずかに拡張する必要があります。
ベクトルaからベクトルbを減算し、ベクトルの成分を正に保ちたい場合、できる最大値はc = a -min( a i / b i ) bです。 この場合、 cのコンポーネントの1つが消えます。 当然、私たちはそれほどバラバラにしたくありません。 2番目から1番目を少し減算するだけです。
alpha = 0.5; basis = {B1[[1]], B1[[2]] - alpha Min[B1[[2]]/B1[[1]]] B1[[1]]}; metric = Outer[Dot, basis, basis, 1];
たとえば、すべてから平均ベクトルを引くことができますが、それは重要ではありません。主なことは、ベクトル間の角度を何らかの方法で増やすことです。 このステップでの自由は、タスクの不確実性に対する避けられない支払いです。 係数0 <
alpha
<1は、アルゴリズムの唯一のフィッティングパラメーターです。 たとえば、投稿の最初に写真を撮るには、
alpha
= 0.95と入力する必要がありました。
metric
行列は、基底ベクトルの線形エンベロープメトリックであり、次のセクションで必要になるグラム行列でもあります。
ベースライン分解
ベースライン分解は標準的な手順です。 唯一の微妙:問題のステートメントから、展開係数が正でなければならないことは明らかです。 正の係数を持つ一連のベクトルの線形スパンは、無限シンプレックス(頂点が原点にあり、基底が無限に続くピラミッド)です。 このシンプレックスの面は、低次元のシンプレックスです。 必要なのは、指定されたベクトルをシンプレックスに投影することです。 ベクトルがシンプレックス内に収まる場合(基底に沿ったすべての展開係数が正の場合)、問題は解決されますが、そうでない場合は、面に投影する必要があります。
ここで、実際には、関数全体:
皮肉に見えるのは、コードを書く私のスタイルだけです。
reduceMetric = Compile[ { {metric, _Real, 2}, {index, _Integer} }, Transpose@Delete[Transpose@Delete[metric, index], index], CompilationTarget -> "C" ]; getComponents = Compile[ { {vec, _Real, 1}, {basis, _Real, 2}, {metric, _Real, 2} }, Module[ { covariant, contravariant = Table[0., {Length[basis]}], flag = True, subspace }, covariant = basis.vec; flag = If[ Det[metric] != 0, contravariant = Inverse[metric].covariant; FreeQ[Sign[contravariant], -1], False ]; Chop@If[ flag, contravariant, subspace = Table[ Insert[ getComponents[vec, Delete[basis, i], reduceMetric[metric, i]], 0., i], {i, 1, Length@basis} ]; subspace[[minIndex[-(subspace.covariant)]]] ] ], { {_minIndex, _Integer}, {_reduceMetric, _Real, 2}, {_getComponents, _Real, 1} }, CompilationTarget -> "C", RuntimeAttributes -> {Listable}, Parallelization -> True ]
正常に動作することを確認します。
getComponents[{0.1, 0.9}.basis, basis, metric] {0.1, 0.9}
以下は、コードを理解したい人へのコメントです。 基底e (i)に沿ったベクトルvの展開係数は、反変座標v = v i e (i)と呼ばれます。 まず、共変座標v i =( e (i) 、 v )を計算します。 メトリックg ij =( e (i) 、 e (j) )が可逆である場合、反変座標は逆メトリックg ij =( g -1 ) ij 、すなわち v i = g ij v j 。 以上です。
flag = False
2つの場合に生成されます:メトリックが不可逆的(予想よりも小さい次元のシンプレックス)または少なくとも1つの反変座標が負(シンプレックス内に収まらない)。 これらの場合、すべての面を愚かに再帰的にソートし、最大になる投影を選択します。 基底e (i)の部分空間への投影は、共変座標と反変座標v i v iの畳み込みです。 確かに。
結果
すべての関数はCでコンパイルされますが、Mathematicaは頑固に複数のコアで
getComponents
を実行することを望みません。 怠lazを理解するには、開発者の良心に任せましょう。 したがって、2,736,000ピクセルすべてを粉砕します。
pixels = Join @@ ImageData[ColorNegate@original]; components = Table[ getComponents[pixel, basis, metric], {pixel, pixels} ];
最初のコンポーネント:
data1 = (({1, 0} #).basis) & /@ components; ColorNegate[Image@Partition[data1, sizeX]]
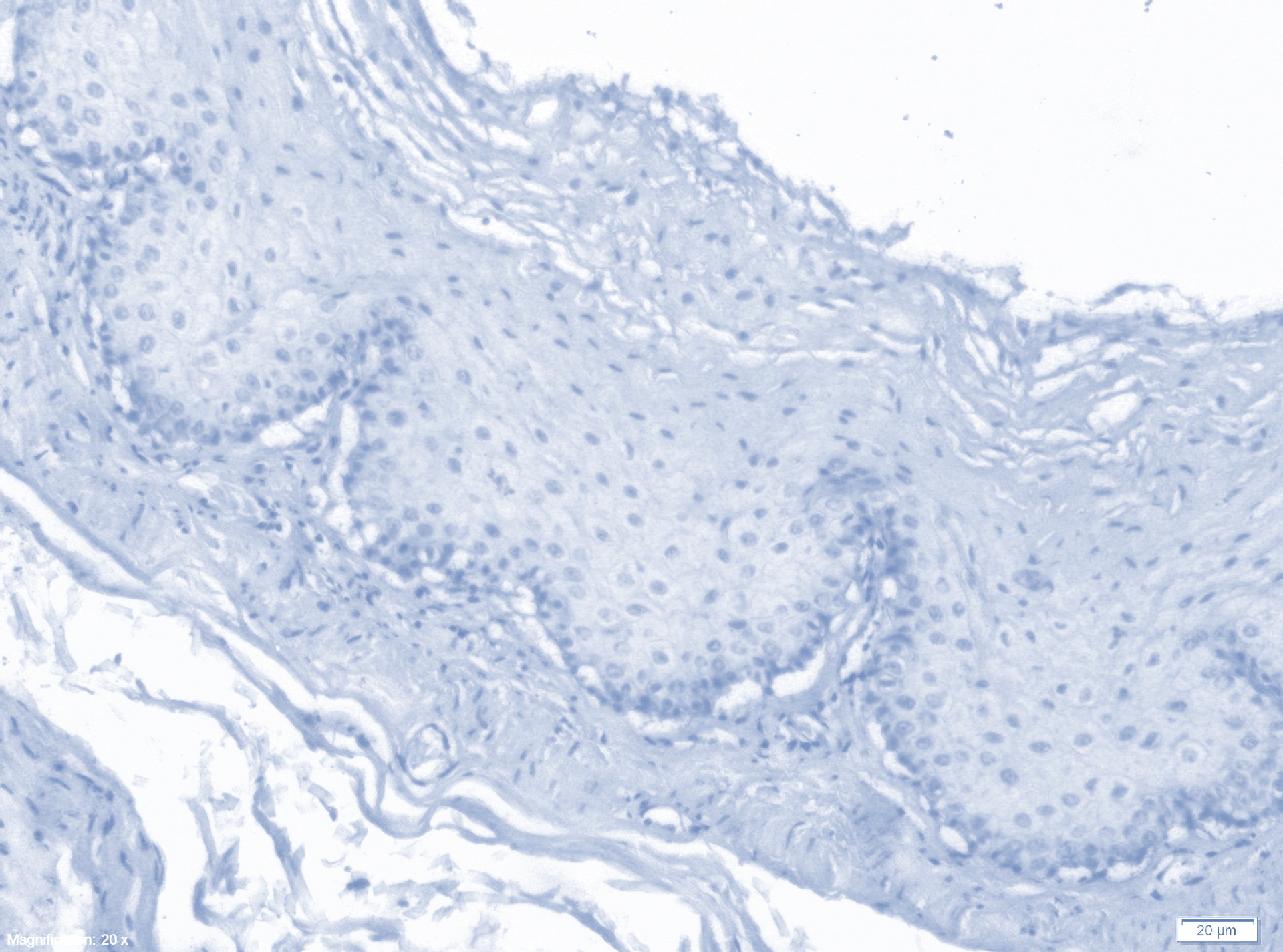
2番目のコンポーネント:
data2 = (({0, 1} #).basis) & /@ components; ColorNegate@Image@Partition[data2, sizeX]

もっと持てますか?
できます。
getComponents
で縮退/冗長ベースを
getComponents
さえすれば、あなたは幸せになるでしょう:
Module[ { basis = {{1, 0}, {0, 1}, {1, 1}}, metric }, metric = Outer[Dot, basis, basis, 1]; getComponents[{0.1, 0., 0.9}.basis, basis, metric] ] {0.1, 0., 0.9}
こちらからMathematicaファイルをダウンロードできます。