内容

はじめに

前の記事は、ヤニベコフ効果の数値シミュレーションに関するものでしたが、最初のリアプノフ法にかなり近似しているにもかかわらず、この効果を定性的に研究できることが突然思い浮かびました。しかし、数値モデリングも非常に興味深い質問であり、特に私の研究問題の面にあります。したがって、今日は

最後に、Rodrigue-Hamiltonパラメーターを使用して、空間内の身体の方向を記述する方法を決定します。
自由体の運動方程式の表現形式を考えてみましょう。テンソル方程式を行列および成分方程式に変換する方法を示します。
主慣性モーメント間のさまざまな比率で自由剛体の運動をシミュレートし、ジャニベコフ効果がどのように現れるかを示しましょう。

1.テンソル形式の自由運動の微分方程式

これらの方程式をベクトル形式で繰り返し検討しました

$\ begin {align *}＆amp; m \、\ vec a_ {c} = \ sum \ vec F_k ^ {\、e} \\＆amp; \ mathbf I_c \、\ vec \ epsilon + \ vec \ omega \ times \左（\ mathbf I_c \、\ vec \ omega \ right）= \ sum \ vec M_ {c}（\ vec F_k ^ {\、e}）\ end {align *}$

ベクトル表記は、依存関係の性質の一般的な分析に便利であり、馴染みがあり、特定の用語の意味を示します。ただし、方程式をモデリングに便利な形式にさらに変換するには、テンソル表記に渡します

$\ begin {align *}＆amp; m \、\ left（\ ddot x ^ {\、i} + \ Gamma _ {\、kl} ^ {\、i} \、\ dot x ^ {\、k} \、 \ドットx ^ {\、l} \右）= X ^ {\、i} \\＆amp; I _ {\、j} ^ {\、i} \、\ dot \ omega ^ {j} + \ varepsilon ^ {\、ijk} \、\ omega _ {\、j} \、g _ {\、kl} \、I _ {\、p} ^ {\、l} \、\ omega ^ {\、p} = M ^ { i} \ end {align *}$

どこで $x ^ {\、i}$ -身体の重心の反変座標; $X ^ {\、i}$ -体に適用される外力の主ベクトルの反変成分; $M ^ {\、i}$ -体に加えられる外力の主モーメントの反変成分。

方程式系（2）は既に閉じられており、それを統合することで、重心の運動の法則と時間に対する体の角速度の依存性を得ることができます。しかし、私たちはまだ身体の向きに興味があるので、この方程式系を補足します

$2 \、\ varepsilon ^ {\、ijk} \、\ lambda _ {\、j} \、\ dot \ lambda _ {\、k} + 2 \、\ lambda_0 \、\ dot \ lambda ^ {\、i}- 2 \、\ lambda ^ {\、i} \、\ dot \ lambda_0 = \ omega ^ {\、i}$

方程式（3）は、ロドリゲハミルトン方向パラメーターによる角速度の成分の表現にすぎません。以前の記事ですでにこの表現を受け取っています。次に、方向パラメータを角速度成分に関連付ける微分方程式として考えます。

ただし、Rodrigue-Hamiltonパラメーターは冗長です。4つのパラメーターがあり、3つの座標で空間内の身体の向きを説明できます。また、システム（2）、（3）の未知数の数は、方程式の数を1つ超えています。したがって、式（2）および（3）を方向パラメーター間の関係式で補足する必要があります。 Rodrigue-Hamiltonのパラメーターに関する記事では、身体の回転が単一の四元数によって都合よく記述されることを示しました。

$\ lambda_0 ^ 2 + \ lambda_1 ^ 2 + \ lambda_2 ^ 2 + \ lambda_3 ^ 2 = 1$

または、テンソル形式

$\ lambda_0 ^ 2 + \ lambda _ {\、i} \、\ lambda ^ {\、i} = 1$

（4）を時間で区別します

$2 \、\ lambda_0 \、\ dot \ lambda_0 + \ dot \ lambda _ {\、i} \、\ lambda ^ {\、i} + \ lambda _ {\、i} \、\ dot \ lambda ^ {\、i } = 0$

スカラー積の可換性を考えると、 $\ dot \ lambda _ {\、i} \、\ lambda ^ {\、i} = \ lambda _ {\、i} \、\ dot \ lambda ^ {\、i}$ それから

$\ lambda_0 \、\ dot \ lambda_0 + \ lambda _ {\、i} \、\ dot \ lambda ^ {\、i} = 0$

望ましいコミュニケーションの方程式があります。テンソル形式の自由剛体の完全な運動方程式系は、次の形式になります。

$\ begin {align *}＆amp; \ dot x ^ {\、i}-v ^ {\、i} = 0 \\＆amp; m \、\ left（\ dot v ^ {\、i} + \ Gamma_ { \、kl} ^ {\、i} \、v ^ {\、k} \、v ^ {\、l} \右）= X ^ {\、i} \\＆amp; 2 \、\ varepsilon ^ { \、ijk} \、\ lambda _ {\、j} \、\ dot \ lambda _ {\、k} + 2 \、\ lambda_0 \、\ dot \ lambda ^ {\、i}-2 \、\ lambda ^ { \、i} \、\ dot \ lambda_0-\ omega ^ {\、i} = 0 \\＆amp; \ lambda_0 \、\ dot \ lambda_0 + \ lambda _ {\、i} \、\ dot \ lambda ^ {\ 、i} = 0 \\＆amp; I _ {\、j} ^ {\、i} \、\ dot \ omega ^ {j} + \ varepsilon ^ {\、ijk} \、\ omega _ {\、j} \ 、g _ {\、kl} \、I _ {\、p} ^ {\、l} \、\ omega ^ {\、p} = M ^ {i} \ end {align *}$

かなり怖い-（6）13個の未知の量を持つ13個の非線形1次微分方程式が含まれています。一般的なテンソル表記のために恐ろしいように見えますが、特定の座標（この場合はデカルト座標）に移動すると、システム（6）は大幅に簡略化されます。

2.デカルトベースの剛体の運動の微分方程式の行列形式

身体の位相座標の列ベクトルを導入します

$\ mathbf y = \ begin {bmatrix} \ mathbf x ^ T＆amp;＆amp; \ mathbf q ^ T＆amp;＆amp; \ mathbf v ^ T＆amp;＆amp; \ mathbf \ omega ^ T \ end {bmatrix} ^ T$

どこで $\ mathbf x = \ begin {bmatrix} x_c＆amp;＆amp; y_c＆amp;＆amp; z_c \ end {bmatrix} ^ T$ そして $\ mathbf v = \ begin {bmatrix} v_ {cx}＆amp;＆amp; v_ {cy}＆amp;＆amp; v_ {cz} \ end {bmatrix} ^ T$ -体の重心の位置と速度; $\ mathbf q = \ begin {bmatrix} \ lambda_0＆amp;＆amp; \ lambda_1＆amp;＆amp; \ lambda_2＆amp;＆amp; \ lambda_3 \ end {bmatrix} ^ T$ そして $\ mathbf \ omega = \ begin {bmatrix} \ omega_x＆amp;＆amp; \ omega_y＆amp;＆amp; \ omega_z \ end {bmatrix} ^ T$ -身体の向きと角速度。

デカルト基底では、計量テンソルは単位行列で表され、クリストッフェル記号はゼロに等しいため、方程式系（6）は次のように行列形式で記述できます。

$\ begin {align *}＆amp; \ mathbf {\ dot x}-\ mathbf v = \ mathbf 0 \\＆amp; 2 \、\ mathbf B \、\ mathbf {\ dot q}-\ mathbf D \、\ mathbf \ omega = \ mathbf 0 \\＆amp; m \ mathbf {\ dot v} = \ mathbf X \\＆amp; \ mathbf I_c \、\ mathbf {\ dot \ omega} + \ mathbf \ Omega \、\ mathbf I_c \、\ mathbf \ omega = \ mathbf M_c \ end {align *}$

行列が導入される場所

$\ mathbf B = \ begin {bmatrix} \ lambda_0＆amp;＆amp; \ lambda_1＆amp;＆amp; \ lambda_2＆amp;＆amp; \ lambda_3 \\-\ lambda_1＆amp;＆amp; \ lambda_0＆amp;＆amp; -\ lambda_3＆amp;＆amp; \ lambda_2 \\-\ lambda_2＆amp;＆amp; \ lambda_3＆amp;＆amp; \ lambda_0＆amp;＆amp; -\ lambda_1 \\-\ lambda_3＆amp;＆amp; -\ lambda_2＆amp;＆amp; \ lambda_1＆amp;＆amp; \ lambda_0 \\ \ end {bmatrix}、\ quad \ mathbf D = \ begin {bmatrix} \ mathbf 0 ^ T \\ \ mathbf E \ end {bmatrix}、\ quad \ mathbf \ Omega = \ begin {bmatrix} 0 ＆amp;＆amp; -\ omega_z＆amp;＆amp; \ omega_y \\ \ omega_z＆amp;＆amp; 0＆amp;＆amp; -\ omega_x \\-\ omega_y＆amp;＆amp; \ omega_z＆amp;＆amp; 0 \ end {bmatrix}$

一次微分に関してシステム（7）を解くと、

$\ begin {align *}＆amp; \ mathbf {\ dot x} = \ mathbf v \\＆amp; \ mathbf {\ dot q} = \ frac {1} {2} \、\ mathbf B ^ {-1} \、\ mathbf D \、\ mathbf \ omega \\＆amp; \ mathbf {\ dot v} = \ frac {1} {m} \、\ mathbf X \\＆amp; \ mathbf {\ dot \ omega} = \ mathbf I_c ^ {-1} \、\ left（\ mathbf M_c-\ mathbf \ Omega \、\ mathbf I_c \、\ mathbf \ omega \ right）\ end {align *}$

コーシーの形の運動方程式系。

3.ジャニベコフの効果のモデリング

外力要因がない場合、システム（8）の右側はゼロであり、重心の運動方程式は初期条件を考慮して簡単に統合されます。

$\ mathbf x（t）= \ mathbf x_0 + \ mathbf v_0 \、t$

ナットの回転は、（8）から得られる7つの1次方程式のシステムによって記述され、無次元の慣性モーメントを導入します。 $i_y = \ frac {I_y} {I_x}$ そして $i_z = \ frac {I_z} {I_x}$

$\ begin {align *}＆amp; \ dot \ lambda_0 =-\ frac {1} {2} \、\ left（\ lambda_1 \、\ omega_x + \ lambda_2 \、\ omega_y + \ lambda_3 \、\ omega_z \ right） \\＆amp; \ dot \ lambda_1 = \ frac {1} {2} \、\ left（\ lambda_0 \、\ omega_x + \ lambda_3 \、\ omega_y-\ lambda_2 \、\ omega_z \ right）\\＆amp; \ドット\ lambda_2 =-\ frac {1} {2} \、\左（\ lambda_3 \、\ omega_x-\ lambda_0 \、\ omega_y-\ lambda_1 \、\ omega_z \ right）\\＆amp; \ dot \ lambda_3 = \ frac {1} {2} \、\ left（\ lambda_2 \、\ omega_x-\ lambda_1 \、\ omega_y + \ lambda_0 \、\ omega_z \ right）\\＆amp; \ dot \ omega_x = \ left（i_y- i_z）\、\ omega_y \、\ omega_z \\＆amp; \ dot \ omega_y = \ frac {i_z-1} {i_y} \、\ omega_x \、\ omega_z \\＆amp; \ dot \ omega_z = \ frac {1 -i_y} {i_z} \、\ omega_x \、\ omega_y \ end {align *}$

システム（9）の数値積分のために、初期条件を設定します

$\ begin {align *}＆amp; \ lambda_0（0）= 1、\ quad \ lambda_1（0）= \ lambda_2（0）= \ lambda_3（0）= 0 \\＆amp; \ omega_x（0）= \ omega_0、 \ quad \ omega_y（0）= \ Delta \ omega_y、\ quad \ omega_z（0）= 0 \ end {align *}$

どこで $\ omega_0$ -スレッドを離れた後のナットの角速度。 $\デルタ\ omega_y$ -初期角速度摂動

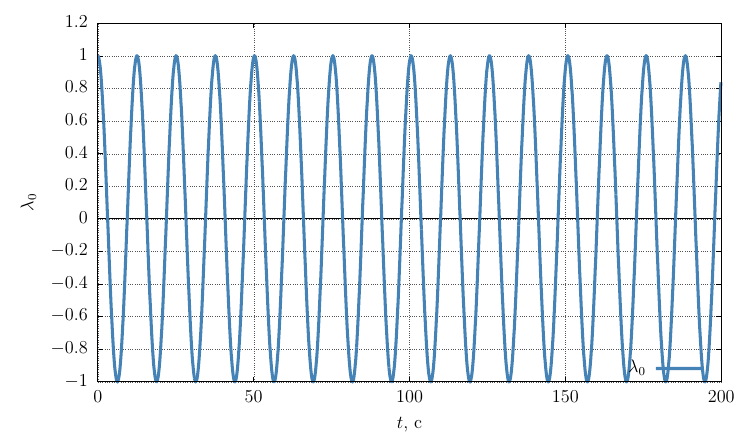
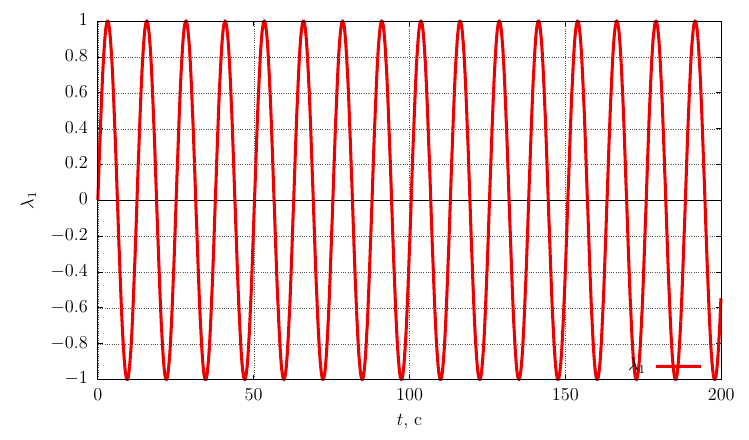
パラメータ値あり $i_y = 2.0、\、i_z = 0.5、\、\ omega_0 = 1.0$ ラジアン/秒 $\ Delta \ omega_y = 1 \ cdot 10 ^ {-10}$ 、rad / s、ナットの動きは次のとおりです

ロドリゲハミルトンの方向パラメーター

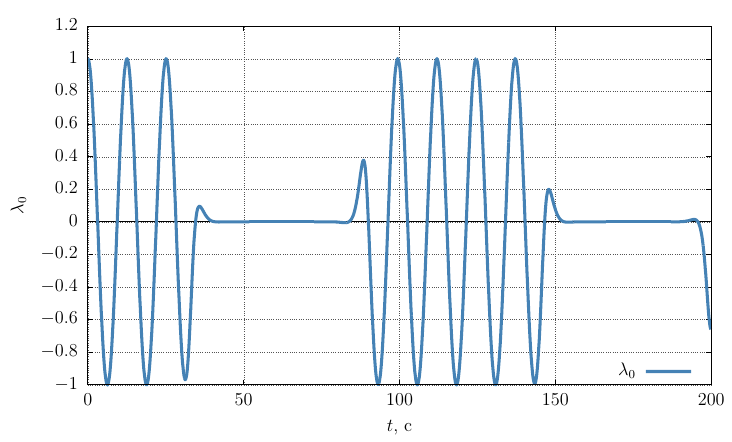
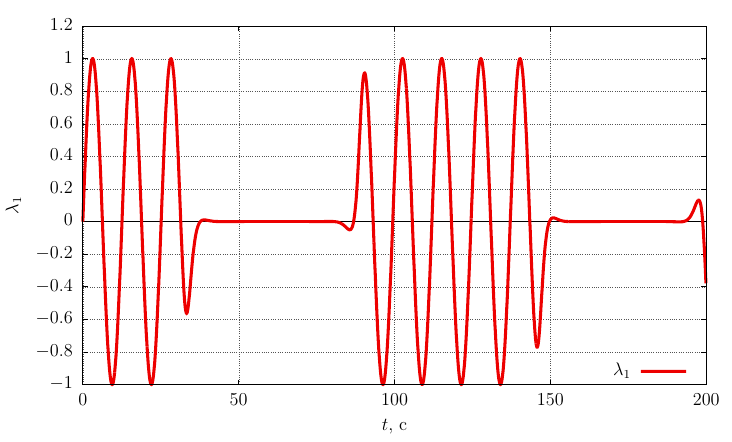
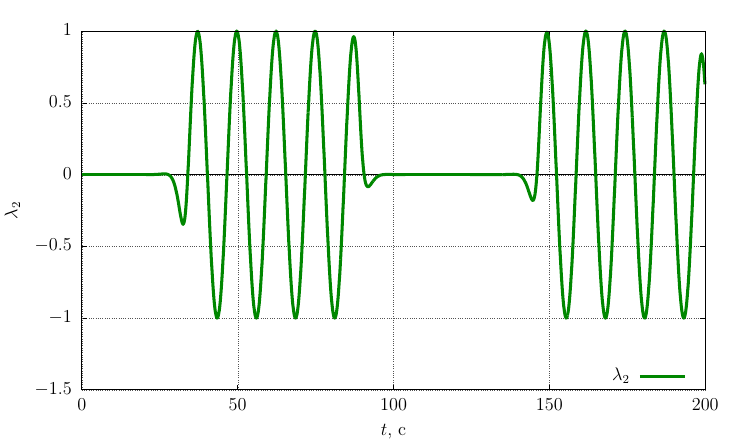
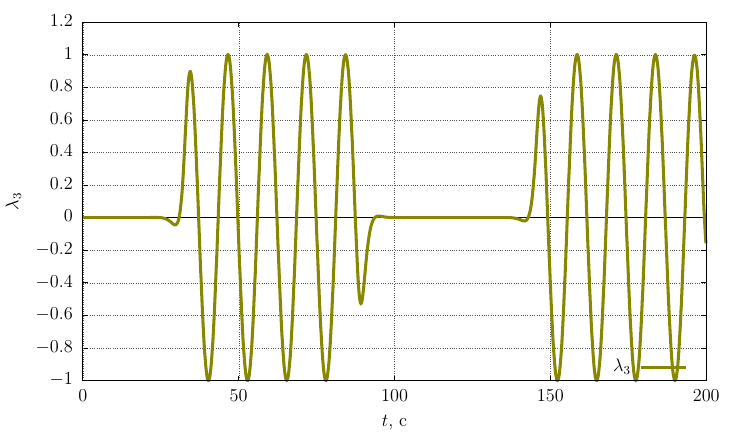
自身の軸上の角速度の投影

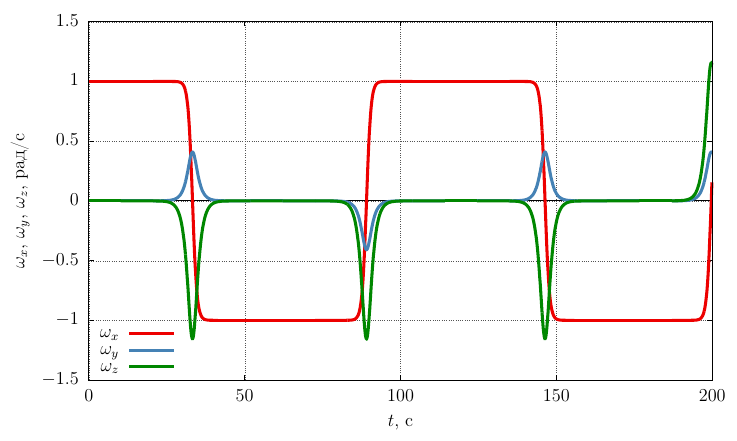
グラフは、 $I_y＆gt; I_x＆gt; I_z$ 、角速度ベクトルのごくわずかな摂動により、空間内のナットの向きに周期的な雪崩のような変化が生じます。

結果を、軸の周りにねじれた体の動きと、最大慣性モーメントで比較します。つまり、 $I_x＆gt; I_y = I_z$ 以下のパラメーター値を設定することにより $i_y = 0.5、\、i_z = 0.5、\、\ omega_0 = 1.0$ ラジアン/秒 $\ Delta \ omega_y = 1 \ cdot 10 ^ {-2}$ ラジアン/秒

ロドリゲハミルトンの方向パラメーター

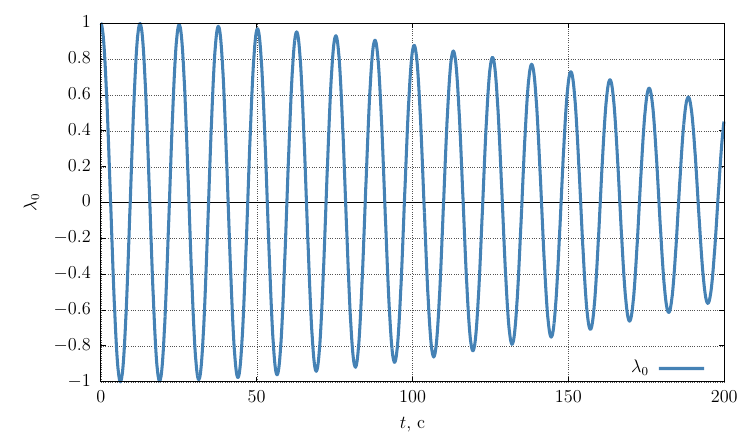
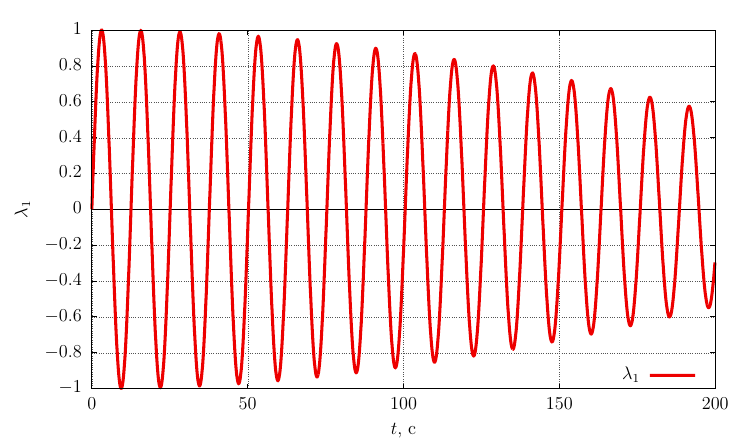
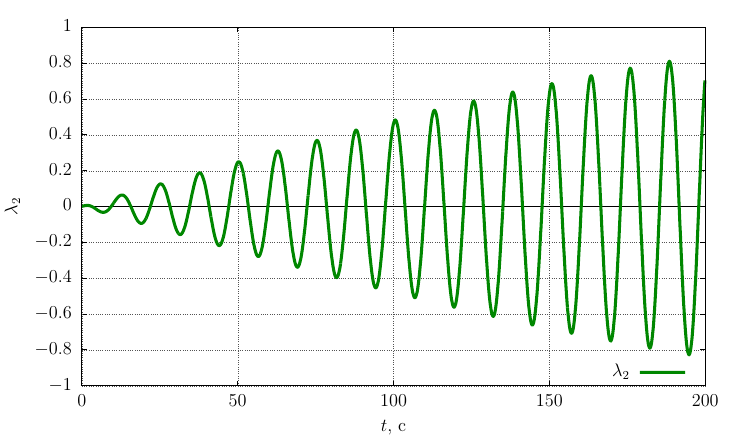
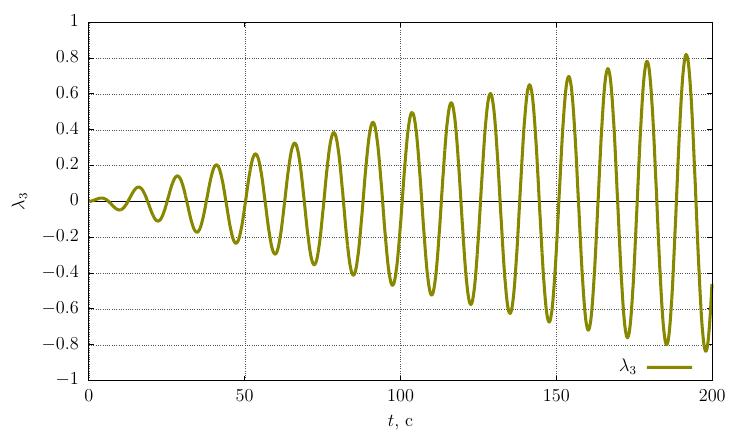
自身の軸上の角速度の投影

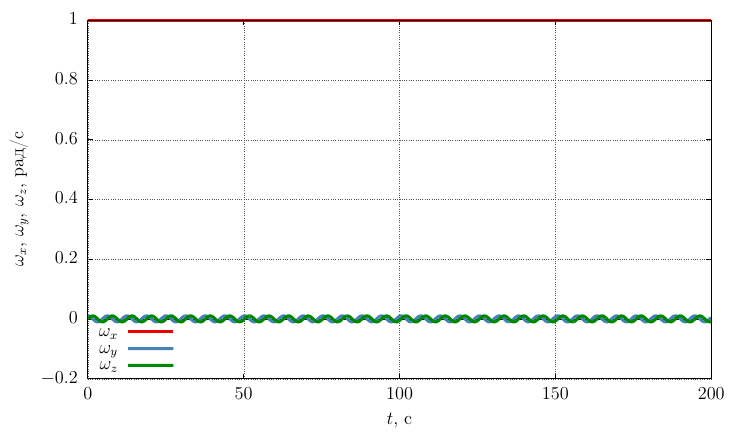
角速度の十分に大きな摂動により、運動は軸の周りの安定した回転のままであることがわかります。 $x$ 少し歳差で。

同様の画像が、慣性モーメントが最小の軸の周りにねじれた物体に対して観察されます（ $I_x＆lt; I_y = I_z$ ） $i_y = 1.5、\、i_z = 1.5、\、\ omega_0 = 1.0$ ラジアン/秒 $\ Delta \ omega_y = 1 \ cdot 10 ^ {-2}$ ラジアン/秒

ロドリゲハミルトンの方向パラメーター

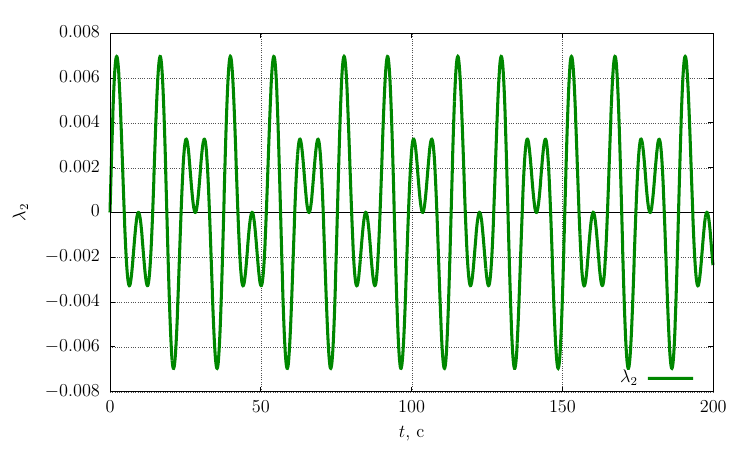
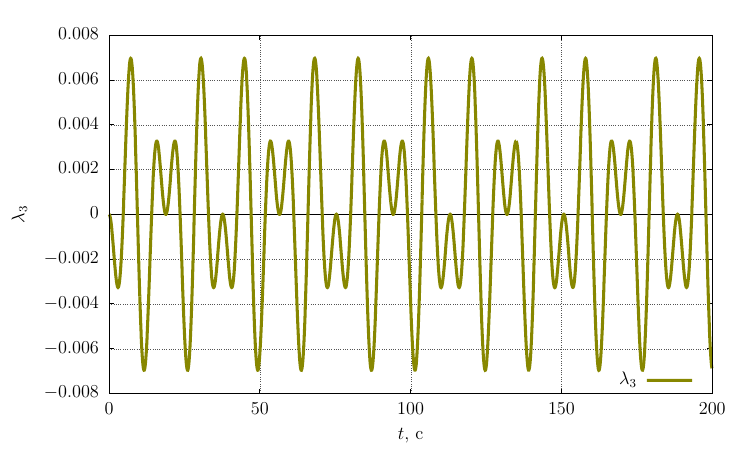
自身の軸上の角速度の投影

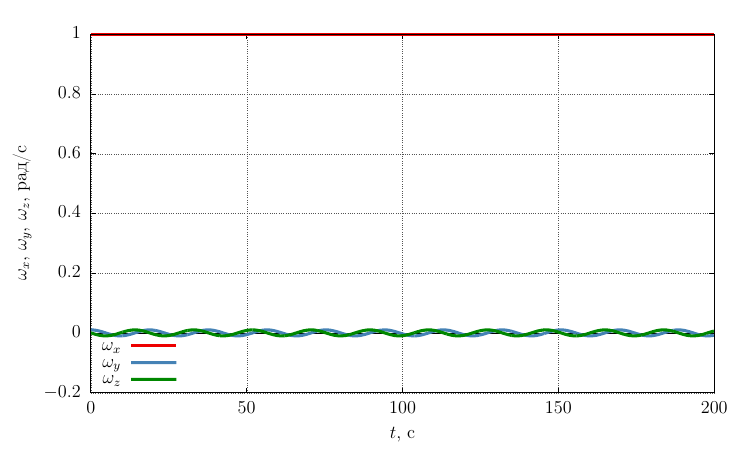
歳差振動数は、最大慣性モーメントを持つ軸を中心にねじる場合よりも大幅に低くなります。これは、ケースよりも大きな慣性モーメントを持つ軸を中心に振動が発生するためです。 $I_x＆gt; I_y = I_z$ 。

おわりに

すべての計算は、著者がSKA Maple 18で実行しました。グラフは、Kile + LaTeX + gnuplotバンドルを使用して計算ログから作成されます。

私もアニメーションを作りたいと思っていますが、この問題に関する著者の経験は非常に少ないです。したがって、読者に質問をしたいと思います-時間に応じて一連の方向の四元数パラメータの体の動きを示すアニメーションクリップを作成するために使用できるソフトウェア（Linux / Windows用）はありますか？これはBlender 3Dでできると思うが、よく分からない。

それまでの間、ご清聴ありがとうございました！

更新：

謝辞

ただし、この記事（および以前の記事）は、 parpalakが開発したMarkdown＆LaTeX Editor Webアプリケーションを使用して作成されたことを完全に忘れていました。このシステムでは、MakdownとLaTeXで記事を入力し、Habraエディターに直接挿入するのに適したコードを生成できます。製品テストに参加してくれた著者に感謝します。彼の許可を得て、私はこのシステムを記事の数学的テキストの作成に使用することをお勧めします

継続するには...

テンソル代数の魔法：パート18-ジャニベコフ効果の数学的モデリング

内容

はじめに

1.テンソル形式の自由運動の微分方程式

2.デカルトベースの剛体の運動の微分方程式の行列形式

3.ジャニベコフの効果のモデリング

おわりに

謝辞

More articles: