はじめに
この記事の執筆時点では、オープンデータに基づいたほとんどのアプリケーション(公式Webサイトdata.mos.ru/appsおよびdata.gov.ruにあります )は、明確な視覚化を備えた都市または集落のインフラストラクチャに関する対話型ガイドであり、多くの場合、最適なルートを選択するオプションがあります。 この出版物およびその後の出版物の目的は、以下を含むオープンデータ分析戦略の議論にコミュニティの注意を引くことです。 予測、統計モデルの構築、および明示的に提示されていない情報の抽出を目的としています。 使用されるツールは、R言語とRStudio開発環境です。
Rを使用する単純さの例として、小さな例を検討し、 ウリヤノフスクで2013年の英国、HOAを誘致するためのレジストリを地図上に視覚化します 。 このデータセットには、さまざまな管理会社の罰金に関する情報が含まれています。 視覚化のために、データセットで提示されたすべての時間について、発言の数、ルーブルの罰金と罰則の数が選択されました。 このデータ(および私に出会ったオープンソースからのその他すべてのデータ)には、多くの省略、タイプミスなどがある傾向があります。 したがって、 前処理されたデータは Rにロードされます。
ulyanovsk.data <- read.csv('./data/formated_tsj.csv')
視覚化には、Googleマップへのインターフェースとggplot2ライブラリが使用され、gridExtraは出力デバイスでグラフを整理するために使用されます。
コード
ライブラリ(ggmap)
ライブラリ(ggplot2)
ライブラリ(gridExtra)
ライブラリ(ggplot2)
ライブラリ(gridExtra)
データセットには緯度と経度に関する情報を含む緯度と経度の列があります。 ウリヤノフスクのマップだけでなく、その部分だけが必要です。その座標はサンプルに含まれています。
コード
ボックス<-make_bbox(lon、lat、data = ulyanovsk.data)
ulyanovsk.map <-get_map(location = 'ulyanovsk'、zoom = calc_zoom(ボックス))
p0 <-ggmap(ulyanovsk.map)
p0 <-p0 + ggtitle( "ウリヤノフスクの地図の一部")+テーマ(legend.position = "none")
ulyanovsk.map <-get_map(location = 'ulyanovsk'、zoom = calc_zoom(ボックス))
p0 <-ggmap(ulyanovsk.map)
p0 <-p0 + ggtitle( "ウリヤノフスクの地図の一部")+テーマ(legend.position = "none")
カードのルーブルにペナルティを課します(penalties_rub_total salb):
コード
p1 <-ggmap(ulyanovsk.map)
p1 <-p1 + geom_point(データ= ulyanovsk.data、aes(x = lon、y = lat、色= penalties_rub_total、サイズ= penalties_rub_total))
p1 <-p1 + scale_color_gradient(低=「黄色」、高=「赤」)
p1 <-p1 + ggtitle(「ファイン、ルーブル単位」)+テーマ(legend.position =「none」)
p1 <-p1 + geom_point(データ= ulyanovsk.data、aes(x = lon、y = lat、色= penalties_rub_total、サイズ= penalties_rub_total))
p1 <-p1 + scale_color_gradient(低=「黄色」、高=「赤」)
p1 <-p1 + ggtitle(「ファイン、ルーブル単位」)+テーマ(legend.position =「none」)
細かい罰金の数:
コード
p2 <-ggmap(ulyanovsk.map)
p2 <-p2 + geom_point(データ= ulyanovsk.data、aes(x = lon、y = lat、色= penalties_total、サイズ= penalties_total))
p2 <-p2 + scale_color_gradient(低=「黄色」、高=「赤」)
p2 <-p2 + ggtitle(「罰金の数」)+テーマ(legend.position =“ none”)
p2 <-p2 + geom_point(データ= ulyanovsk.data、aes(x = lon、y = lat、色= penalties_total、サイズ= penalties_total))
p2 <-p2 + scale_color_gradient(低=「黄色」、高=「赤」)
p2 <-p2 + ggtitle(「罰金の数」)+テーマ(legend.position =“ none”)
断片的な口頭コメントの数:
コード
p3 <-ggmap(ulyanovsk.map)
p3 <-p3 + geom_point(データ= ulyanovsk.data、aes(x = lon、y = lat、色= oral_comments_total、size = oral_comments_total))
p3 <-p3 + scale_color_gradient(低=「黄色」、高=「赤」)
p3 <-p3 + ggtitle(「口頭コメントの数」)+テーマ(legend.position =“ none”)
p3 <-p3 + geom_point(データ= ulyanovsk.data、aes(x = lon、y = lat、色= oral_comments_total、size = oral_comments_total))
p3 <-p3 + scale_color_gradient(低=「黄色」、高=「赤」)
p3 <-p3 + ggtitle(「口頭コメントの数」)+テーマ(legend.position =“ none”)
すべてを一緒に構築します。
grid.arrange(p0, p1, p2, p3, ncol=2)

ドットのサイズと赤の量は、パラメータとともに単調に増加します(たとえば、細かい粒子ほど、ドットが大きくなり、ドットが赤くなります)。 グラフは、調査対象のデータセットでは、ウリヤノフスクの右岸の管理会社が左からより多くの罰金とコメントを持っていることを示しています。
事故統計の研究
このセクションでは、 単一の部門間情報および統計システムからのデータを使用します。 データセットには、2011年から2014年のロシア連邦の地域における10万人あたりの交通事故による死亡率が含まれています。
コード
事故<-read.csv( './ data / accidents.csv')
頭(事故)
頭(事故)

地域ごとの各年の平均:
apply(accidents[,2:5],2,FUN = mean)
## y2011 y2012 y2013 y2014
## 21.36942 21.55694 20.18582 20.34727
ヒストグラム:
コード
ライブラリ(reshape2)
accidents.melt <-melt(事故[、2:5])
ggplot(accidents.melt、aes(x = value、fill = variable))+ geom_histogram(alpha = 0.3)
accidents.melt <-melt(事故[、2:5])
ggplot(accidents.melt、aes(x = value、fill = variable))+ geom_histogram(alpha = 0.3)
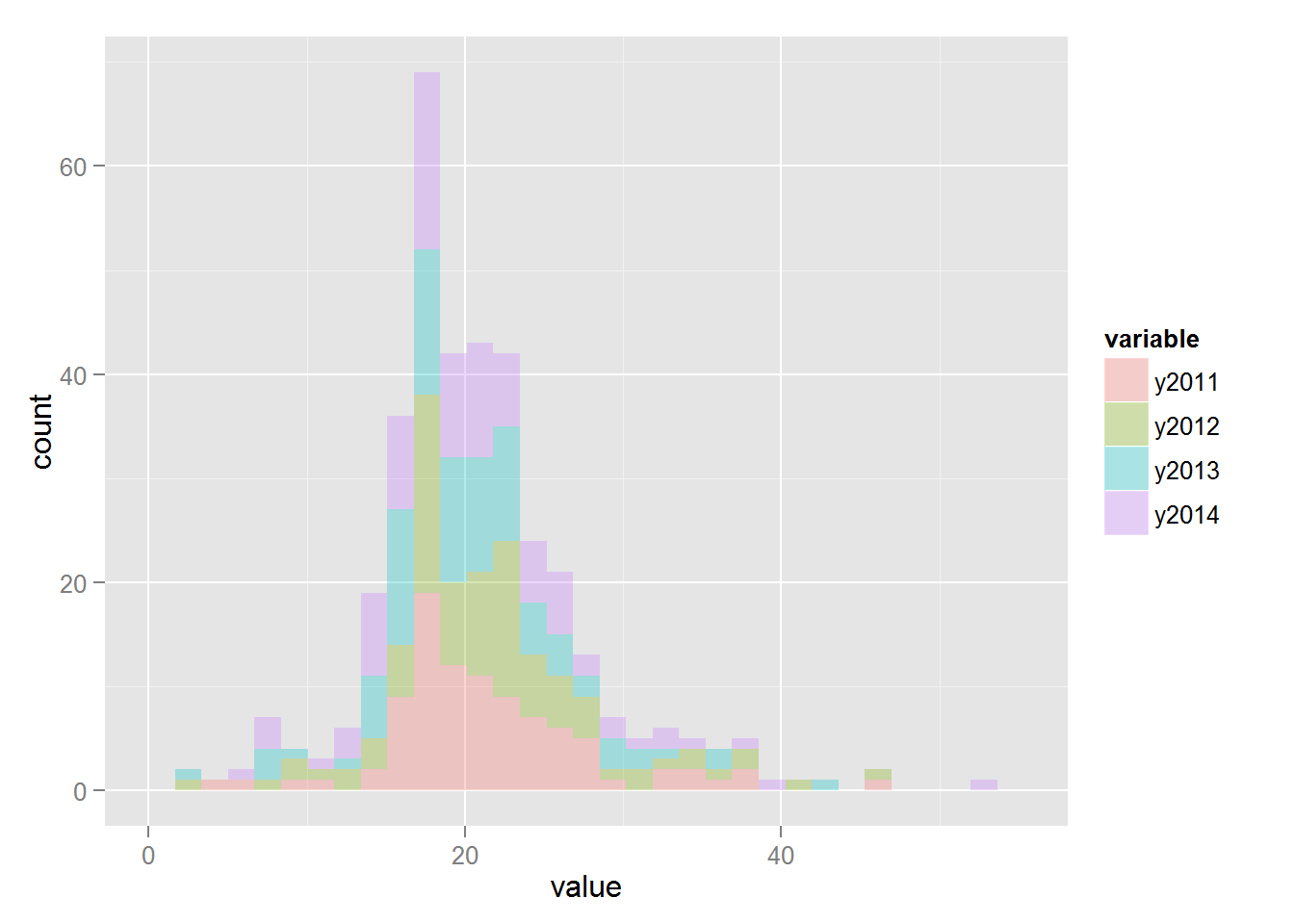
メルト関数は、インジケーターの値が値の列に保存されるようにデータセットを再編成します。変数の列は、インジケーターが受信された年です。
head(accidents.melt)
異なる年の指標の違いが統計的に有意であるかどうかを比較することは興味深いです。 次のモデルの仮定が受け入れられます。
1)指標の値は、学生の分布に左右されるランダム変数です
2)各年には独自の分布パラメーターがあり、nuは正規性パラメーター、sigmaは分散、muは平均です
3)パラメーターnu、sigma、muも確率変数であり、その分布は年に依存しません
問題の正式な声明:データを使用して、分布パラメーターmuが年によって異なるかどうかを確認します。 ケースのベイズ式を書き出すと(記事を煩雑にしないためにここでは説明しません)、階層モデルを取得します。
1)死亡率(accidents.meltの値フィールド)〜t(mu、sigma、nu)
2)mu | group_id〜N(mu_hyp、sigma_hyp)
3)シグマ| group_id〜Unif(a_hyp、b_hyp | group_id)
4)nu | group_id〜Exp(lambda_hyp)
どこムー| group_id〜N(mu_hyp、sigma_hyp)は、group_idグループのmuパラメーターがmu_hyp、sigma_hypハイパーパラメーターと正規分布することを意味します。
group_id変数は、年に応じて値を取ります(2011年は1、2012年は2など)。
accidents.melt$group_id <- as.numeric(accidents.melt$variable)
Rでのモデリングには、Jags言語へのインターフェースと、DBDA2E-utilities.Rファイルからの補助関数plotPostを使用します。これは、 こちら (著者-John Kruschke)にあります。
コード
ライブラリ(rjags)
ソース( 'DBDA2E-utilities.R')
ソース( 'DBDA2E-utilities.R')
モデルの記述はジャグ言語で行われるため、最初にファイルまたは文字列変数がモデル内でR内に作成されます。
コード
modelString <-'
モデル{
for(i in 1:N)
{
y [i]〜dt(mu [group_id [i]]、1 / sigma [group_id [i]] ^ 2、nu [group_id [i]])
}
for(j in 1:NumberOfGroups)
{
mu [j]〜dnorm(PriorMean、0.01)
sigma [j]〜dunif(1E-1、1E + 1)
nuTemp [j]〜dexp(1/19)
nu [j] <-nuTemp [j] + 1
}
}
''
モデル{
for(i in 1:N)
{
y [i]〜dt(mu [group_id [i]]、1 / sigma [group_id [i]] ^ 2、nu [group_id [i]])
}
for(j in 1:NumberOfGroups)
{
mu [j]〜dnorm(PriorMean、0.01)
sigma [j]〜dunif(1E-1、1E + 1)
nuTemp [j]〜dexp(1/19)
nu [j] <-nuTemp [j] + 1
}
}
''
モデルが指定されると、データとともにジャグが渡されます。
コード
modelJags <-jags.model(file = textConnection(modelString)、
データ=リスト(y = accidents.melt $値、group_id = accidents.melt $ group_id、N =長さ(accidents.melt)、NumberOfGroups = 4、PriorMean =(20))、
n.chains = 8、n.adapt = 1000)
データ=リスト(y = accidents.melt $値、group_id = accidents.melt $ group_id、N =長さ(accidents.melt)、NumberOfGroups = 4、PriorMean =(20))、
n.chains = 8、n.adapt = 1000)
JagsはMCMCを使用し、パラメーターmu、sigma、nuの空間でランダムウォークモデルを実装します。 さらに、結合確率は明示的に考慮されていませんが、パラメーターが特定の値を取る確率はそれらの結合確率に比例します。 したがって、jagsは値mu、sigma、nuのリストを返すため、ヒストグラムを使用してそれらの確率を評価できます。 次の行はモデルを開始し、結果を返します。
コード
更新(modelJags、2000)
要約(samplesCoda <-coda.samples(model = modelJags、variable.names = c(「nu」、「mu」、「sigma」)、n.iter = 50000、thin = 500))
要約(samplesCoda <-coda.samples(model = modelJags、variable.names = c(「nu」、「mu」、「sigma」)、n.iter = 50000、thin = 500))
さまざまな年のパラメーターmuの値に関する質問に答えるために、パラメーター値の差のヒストグラムを検討します。
コード
samplesCodaMatrix <-as.matrix(samplesCoda)
samplesCodaDataFrame <-as.data.frame(samplesCodaMatrix)
samplesCodaDataFrame <-samplesCodaDataFrame [、1:4]
plotPost(samplesCodaMatrix [、1]-samplesCodaMatrix [、2]、cenTend = 'mean'、main = '2011 vs. 2012')
plotPost(samplesCodaMatrix [、1]-samplesCodaMatrix [、3]、cenTend = 'mean'、main = '2011 vs. 2013')
plotPost(samplesCodaMatrix [、1]-samplesCodaMatrix [、4]、cenTend = 'mean'、main = '2011 vs. 2014')
plotPost(samplesCodaMatrix [、2]-samplesCodaMatrix [、3]、cenTend = 'mean'、main = '2012 vs. 2013')
plotPost(samplesCodaMatrix [、2]-samplesCodaMatrix [、4]、cenTend = 'mean'、main = '2012 vs. 2014')
plotPost(samplesCodaMatrix [、3]-samplesCodaMatrix [、4]、cenTend = 'mean'、main = '2013 vs. 2014')
samplesCodaDataFrame <-as.data.frame(samplesCodaMatrix)
samplesCodaDataFrame <-samplesCodaDataFrame [、1:4]
plotPost(samplesCodaMatrix [、1]-samplesCodaMatrix [、2]、cenTend = 'mean'、main = '2011 vs. 2012')
plotPost(samplesCodaMatrix [、1]-samplesCodaMatrix [、3]、cenTend = 'mean'、main = '2011 vs. 2013')
plotPost(samplesCodaMatrix [、1]-samplesCodaMatrix [、4]、cenTend = 'mean'、main = '2011 vs. 2014')
plotPost(samplesCodaMatrix [、2]-samplesCodaMatrix [、3]、cenTend = 'mean'、main = '2012 vs. 2013')
plotPost(samplesCodaMatrix [、2]-samplesCodaMatrix [、4]、cenTend = 'mean'、main = '2012 vs. 2014')
plotPost(samplesCodaMatrix [、3]-samplesCodaMatrix [、4]、cenTend = 'mean'、main = '2013 vs. 2014')
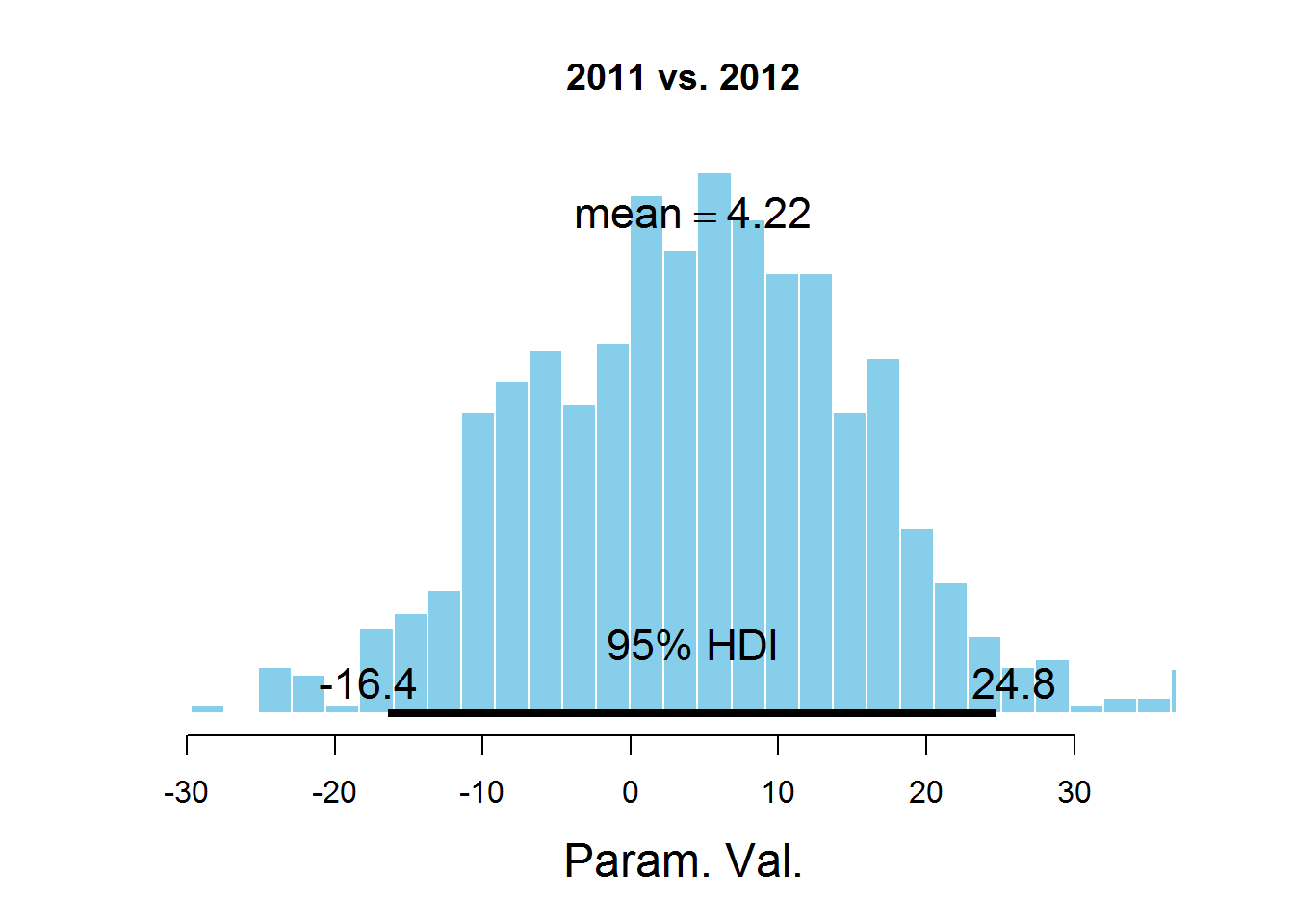

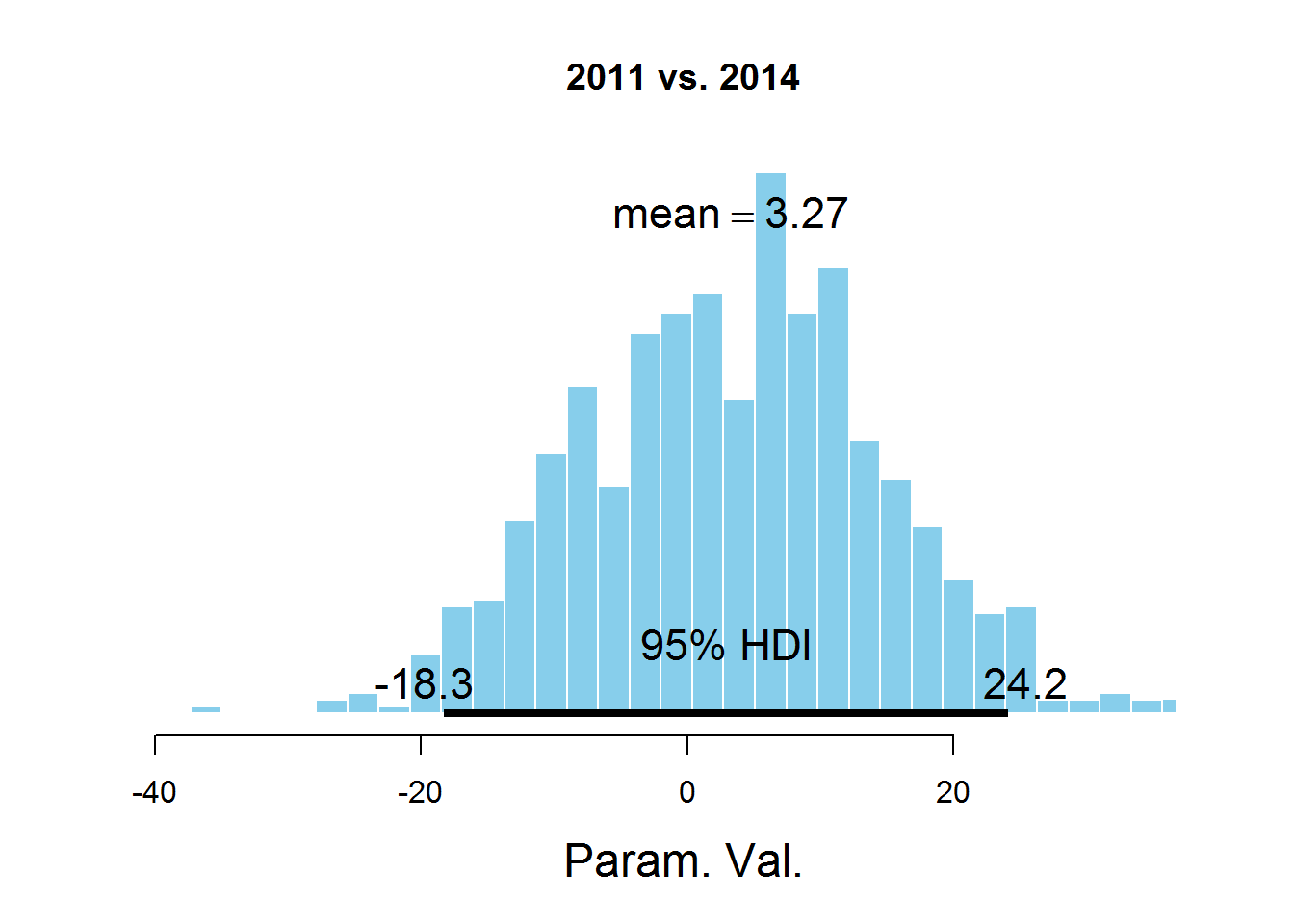
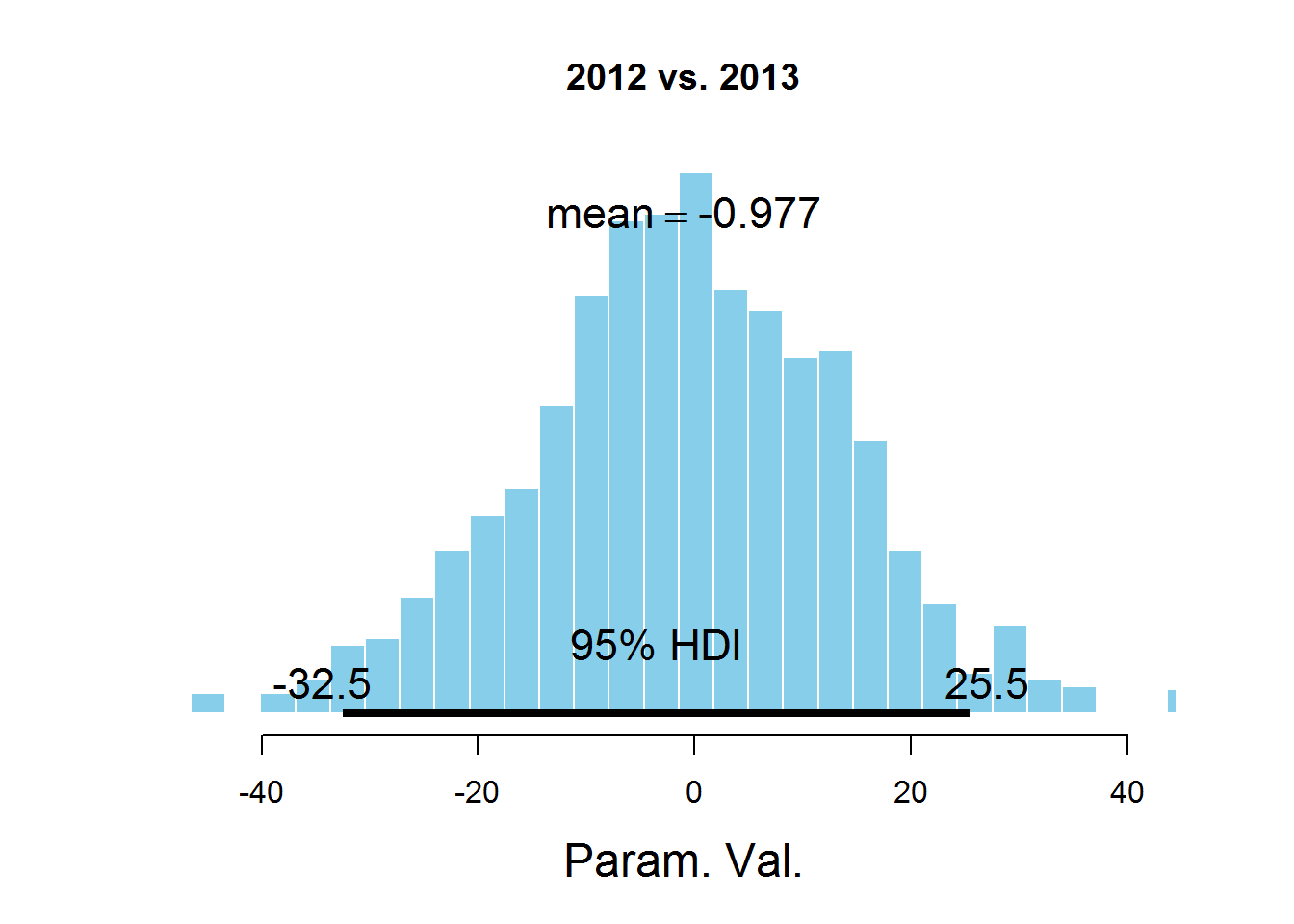
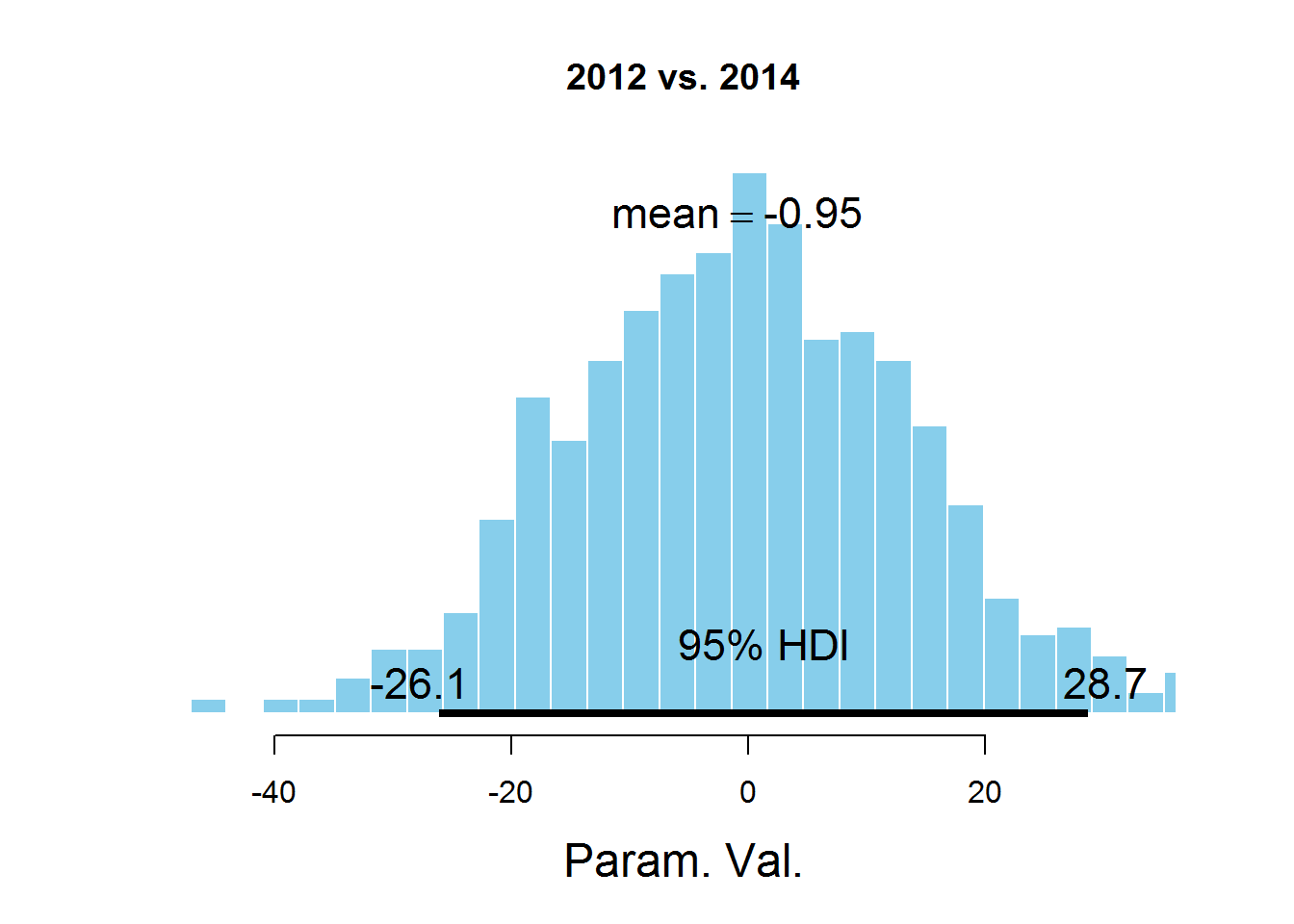
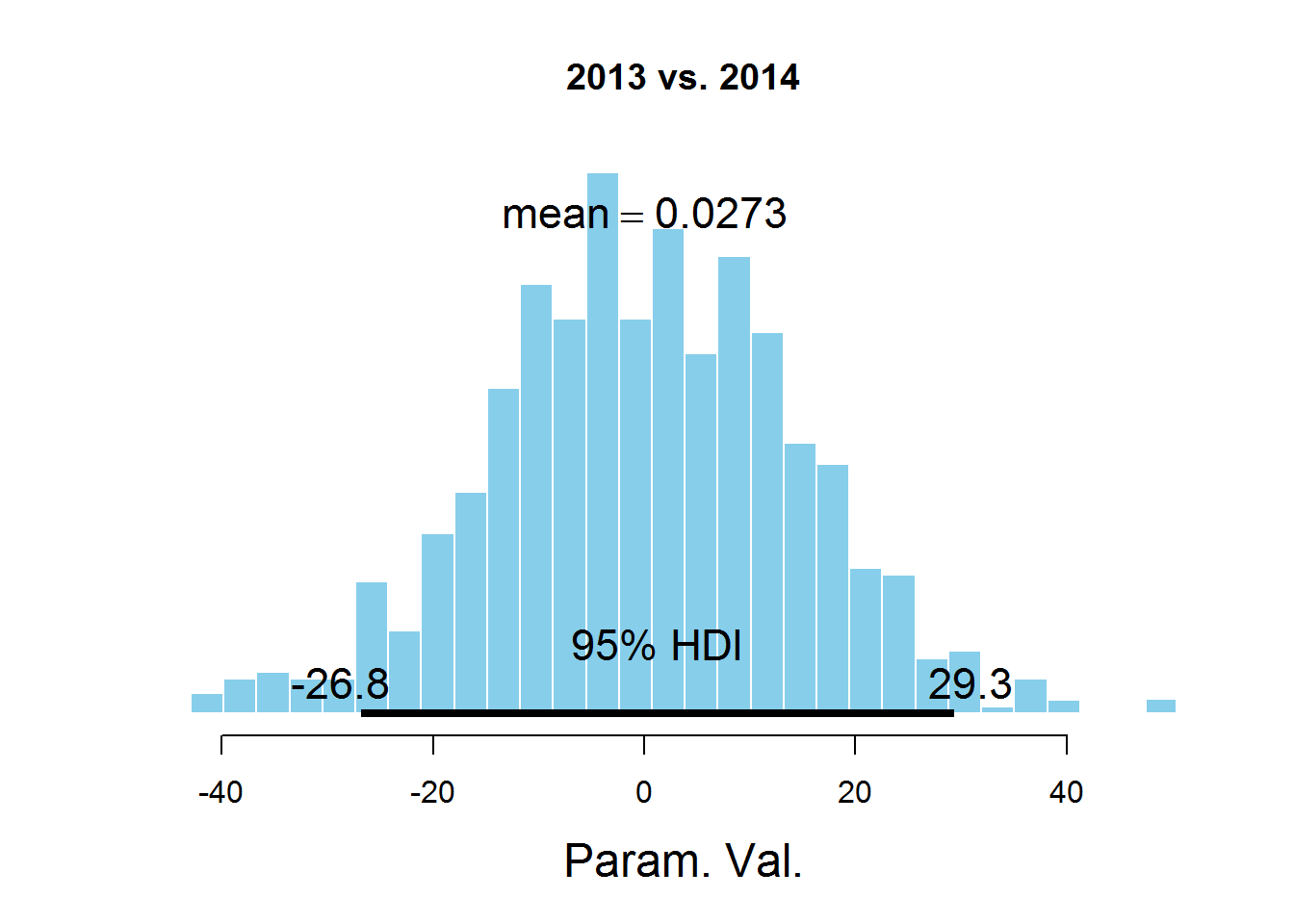
グラフは、HDI間隔、間隔外の値よりも可能性の高い値を示し、これらの値の確率の合計は0.95です。 値0はHDIに該当することがわかります。これは、パラメータmuがデータセットで表されるすべての年で同じであることを示唆しています。 ここには議論の余地がある点があります-HDI値は、サブジェクト領域の知識に従って選択されます。 このタスクでは、おそらく95%の値は最適ではありません。